PARABOLA-10
Examples
1. If the chord of contact of tangent from a point
(a) Parabola
(b) Hyperbola
(c) ellipse
(d) Circle
Show Answer
Solution: Let the point
Now this chord is tangent of parabola
Equation of tangent
From (1) and (2) we get
So, Equation of parabola becomes
Locus of
Answer: b
2. Let
(a)
(b) the point
(c) the point
(d) None of these
Show Answer
Solution:
Let
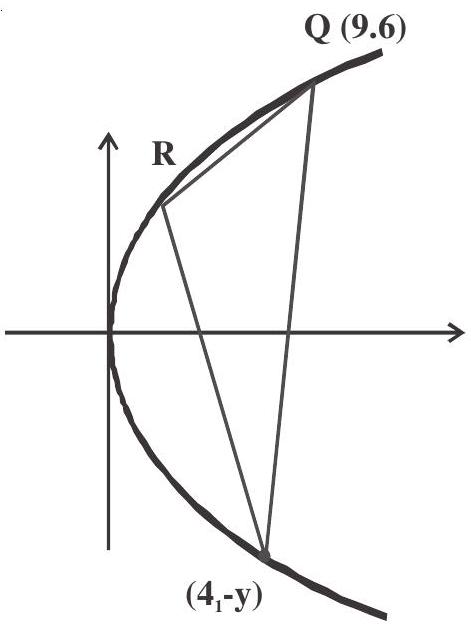
Area is maximum when
Coordinates of
Answer: c
3. Minimum area of circle which touches the parabola’s
(a)
(b)
(c)
(d)
Show Answer
Solution:
tangent at point.
Area of circle

Answer: a
4. The equation of the common tangents to the parabola
(a)
(b)
(c)
(d)
Show Answer
Solution: Let
Equation of tangent are
Answer: a, b
5.
| Column I | Column II |
|---|---|
| i. Area of |
(a). |
| ii. Radius of circum circle of |
(b). |
| iii. Centroid of |
(c). |
| iv. Circum centre of |
(d) |
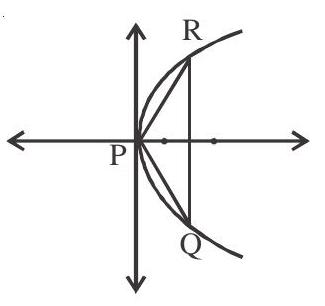
Show Answer
Solution: Equation of normal is
It passes through
Points are given by
i.e.
area of
Centroid
Circum centre
Comprehension based Questions (Exampels 6 to 8)
Comprehension: 1
Consider the circle
6. The ratio of the area of the triangles
(a)
(b)
(c)
(d)
Show Answer
Solution: Point of intersection of circle & parabola
Q
Tangent to the parabola at
Tangent to the circle at
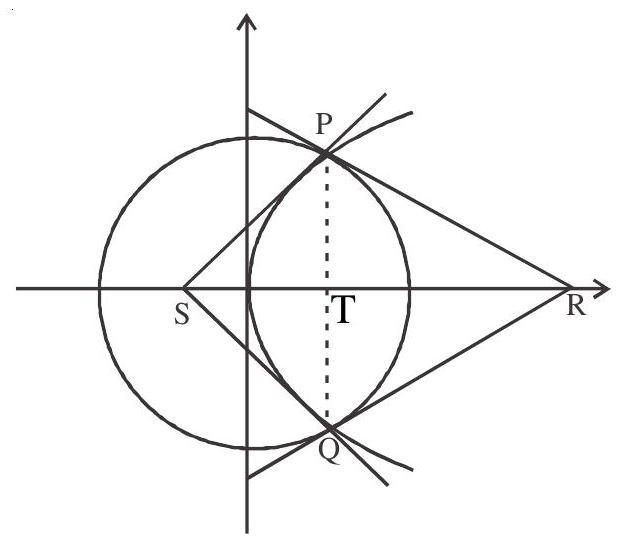
Answer: c
7. The radius of the circum circle of the triangle PRS is
(a)
(b)
(c)
(d)
Show Answer
Solution: area
Answer: b
8. The radius of the in circle of the triangle
(a) 4
(b) 3
(c)
(d) 2
Show Answer
Solution:
Answer: d
Comprehension based Questions (Exampels 9 to 11)
Comprehension: 2
If
9. If
(a)
(b)
(c)
(d)
10. If
(a)
(b)
(c)
(d)
11. If
(a)
(b)
(c)
(d)
Show Answer
Solution:
9.
Answer: c
10. If
Answer: a
11. If
Since it lies on the line
Answer: b
Practice questions
1. The point
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)2. The shortest distance between the parabola
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)3. If normals are drawn from a point
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)4. If
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)5. The equation of the tangent at the vertex of the parabola
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)6. The common tangent to the parabolas
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)7. The shortest distnae between the parabolas
(a)
(b)
(c)
(d) none of these
Show Answer
Answer: (a)8. The largest value of a for which the circle
(a) 4
(b)
(c)
(d)
Show Answer
Answer: (d)Multiple choice questions with one or more than one correct answer.
9. Let
(a)
(b)
(c)
(d)
Show Answer
Answer: (b, c)10. The tangent
(a) vertex is
(b) directrix is
(c) latus rectum is
(d) focus is
Show Answer
Answer: (a, d)Match the following :
11. Consider the parabola
| Column I | Column II |
|---|---|
| A. Equation of tangent can be | p. |
| B. Equation of normal can be | q. |
| C. Equation of chord of contact w.r.t. any point on the directrix | r. |
| D. Equation of chord which subtends right angle at the vertex | s. |
Show Answer
Answer: AAssertion and Reasoning
12. Statement 1 : The curve
Statement 2 : A parabola is symmetric about its axis.
(A) Statement 1 is True, Statement 2 is True; Statement 2 is a correct explanations for statement 1.
(B) Statement 1 is True, statement 2 is true, statement 2 is not a correct explanation for statement 1 .
(C) Statement 1 is true, statement 2 is false.
(D) Statement 1 is false, statement 2 is true.










