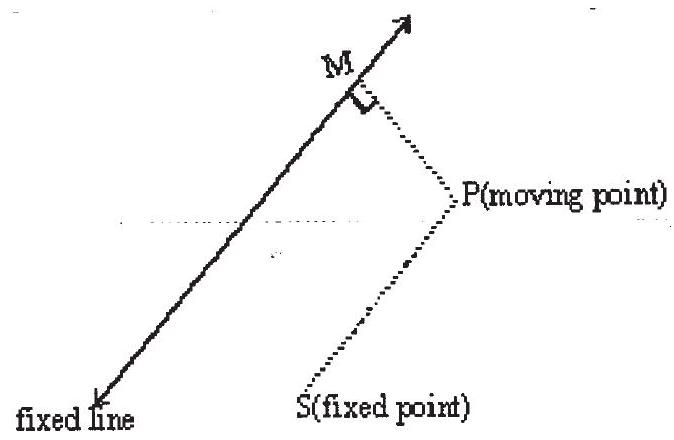
A conic section or conic is the locus of a point $P$ which moves in a plane such that the ratio of its distance from fixed point to the distance from the fixed line always remain same (constant).

$ \frac{P S}{P M}=e $

• The fixed point known as Focus.

• The fixed straight line is known as Directrix,

• The constant ratio is called the Eccentricity denoted by e.

• The line passing through the focus and perpendicular to the directrix is known as axis.

• A point of intersection of a conic with its axis is called a vertex.

• The point which bisects every chord of the conic passing through it, is called the centre of the coni(c).

• The chord passing through the focus and perpendicular to the axis is known as LatusRectum.

General equation of a conic section:

Let coordinates of focus be $S(p, q)$, equation of directrix be $a x+b y+c=0$ and $e$ be the eccentricity of a coni(c). Let $\mathrm{P}(\mathrm{h}, \mathrm{k})$ be a moving point, then by definition.

$\mathrm{SP}=\mathrm{e} \mathrm{PM}$

$\sqrt{(h-p)^{2}+(k-q)^{2}}=e\left|\frac{a h+b k+c}{\sqrt{a^{2}+b^{2}}}\right|$

$\Rightarrow(\mathrm{h}-\mathrm{p})^{2}+(\mathrm{k}-\mathrm{q})^{2}=\mathrm{e}\left(\frac{\mathrm{ah}+\mathrm{bk}+\mathrm{c}}{\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}}\right)^{2}$

Thus locus of $(\mathrm{h}, \mathrm{k})$ is

$(x-p)^{2}+(y-q)^{2}=e^{2} \frac{(a x+b y+c)^{2}}{\left(a^{2}+b^{2}\right)}$

This is equation of conic section which, when simplified, can be written in the form $a x^{2}+2 h x y+b y^{2}+2 g x+2 f y+c=0$ which is general equation of second degree.

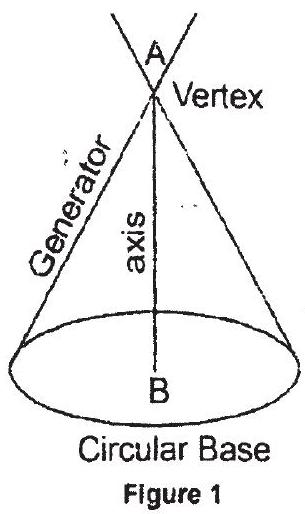
Section of right circular cone by different planes

A right circular cone is as shown in the figure -1

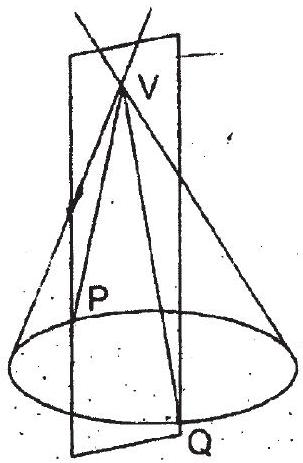
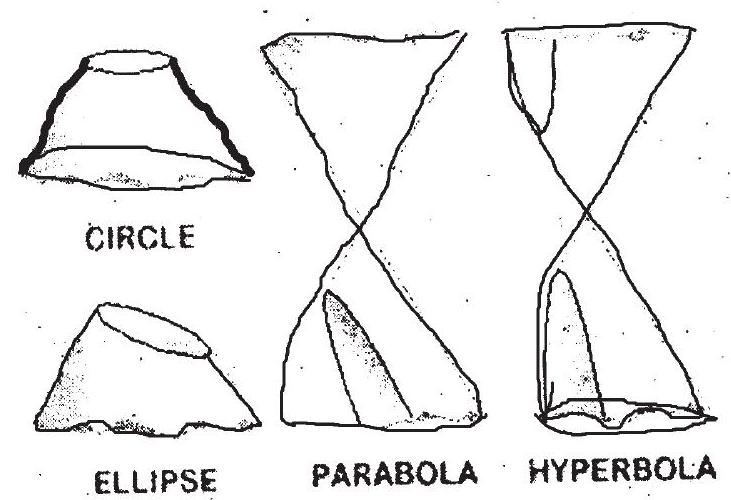
i. Section of a right cone by a plane passing through its vertex is a pair of straight lines passing through the vertex as shown in the figure -2 .

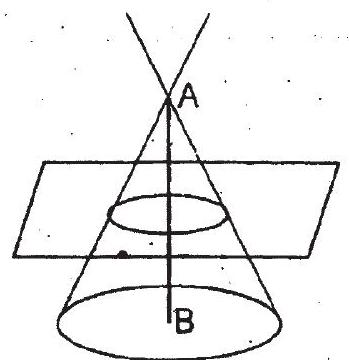
ii. Section of a right circular cone by a plane parallel to its base is a circle as shown in the figure -3 .

iii. Section of a right circular cone by a plane parallel to a generator of the cone is parabola as shown in the figure -4 .

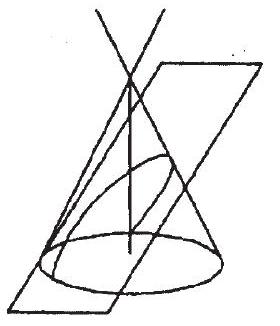
iv. Section of a right circular cone by a plane neither parallel to any generator of the cone nor perpendicular or parallel to the axis of the cone is an ellipse as shown in the figure -5 .

v. Section of a right circular cone by a plane parallel to the axis of the cone is a hyperbola as shown in the figure -6 .

3D View :

Itinguishing various conics:

The nature of the conic section depends upon the position of the focus with respect to the directrix and also upon the value of the eccentricity.

1. If focus lies on the Directrix.

$ \begin{aligned} & \text { If focus lies on the Directrix. } \\ & \Delta \equiv \equiv \mathrm{abc}+2 \mathrm{fgh}-\mathrm{af}^{2}-\mathrm{bg}^{2}-\mathrm{ch}^{2}=0 \quad \Leftarrow=\left|\begin{array}{l} \mathrm{ahg} \\ \mathrm{hbf} \\ \mathrm{g} \mathrm{t} \mathrm{c} \end{array}\right| \end{aligned} $

General equation of a conic represents a pair of straight lines, if

• $\mathrm{h}^{2}>\mathrm{ab}$, the lines will be real and distinct
• $\mathrm{h}^{2}=\mathrm{ab}$, the lines will be coincident
• $\mathrm{h}^{2}<\mathrm{ab}$, the lines will be imaginary (a point)

2. If focus does not lie on Directrix. i. $\Delta \neq 0, \mathrm{a}=\mathrm{b}, \mathrm{h}=0$, a circle

ii. $\Delta \neq 0, \mathrm{e}=1, \mathrm{~h}^{2}=\mathrm{ab}$, a parabola

iii. $\Delta \neq 0,0<\mathrm{e}<1, \mathrm{~h}^{2}<\mathrm{ab}$, an ellipse

iv. $\Delta \neq 0, \mathrm{e}>1, \mathrm{~h}^{2}>\mathrm{ab}$, a hyperbola v. $\Delta \neq 0, \mathrm{e}>1, \mathrm{~h}^{2}>\mathrm{ab}, \mathrm{a}+\mathrm{b}=0$, rectangualr hyperbola

Example: 1 If $\lambda x^{2}+4 x y+y^{2}+\lambda x+3 y+2=0$ represents a equation of parabola then

(a). $\lambda=-4 $

(b). $\lambda=4$

(c). $ \lambda=0$

(d). none of these

Practice questions

1. The locus of a point, which moves such that its distance from the point $(0,-1)$ is twice its distance from the line $3 x+4 y+1=0$ is

(a). $11 x^{2}+11 y^{2}+6 x y+24 x+y+21=0$

(b). $11 x^{2}+39 y^{2}+96 x y+24 x-18 y-21=0$

(c). $39 x^{2}+11 y^{2}+96 x y+24 x+y+21=0$

(d). none of these

2. The equation $25\left(x^{2}+y^{2}-2 x+1\right)=(4 x+3 y-1)^{2}$ represents

(a). a circle

(b). pair of straight lines

(c). a parabola

(d). an ellipse

3. The equation $13 x^{2}+37 y^{2}-18 x y+2 x+14 y-2=0$ represents

(a). a circle

(b). a parabola

(c). a hyperbola

(d). an ellipse

4. If the conic $2 x^{2}+3 y^{2}+x y-3 x+5 y+c=0$ represents a single point then value of $c$ is

(a). $4$

(b). $-4$

(c). $\frac{1}{4}$

(d). $-\frac{1}{4}$