Practice problems

1. Equation of conjugate axis of hyperbola $xy-3y-4x+7=0$ is

(a) $x+y=7$

(b) $x+y=3$

(c) $\mathrm{x}-\mathrm{y}=7$

(d) None of these

Show Answer

Solution:

$\begin{array}{rl}& xy-3y-4x+7=0\\ & xy-3y-4x+12=5\\ & (x-3)(y-4)=5\end{array}$

Equation of asymptotes are $x-3=0$ and $y-4=0$ Since the hyperbola is rectangular hyperbola, axes are bisectors of asymptotes

Hence their slopes are $\pm 1$

$\therefore$ Equation of conjugate axis is

$\begin{array}{rl}& y-4=-1(x-3)\\ & x+y=7\end{array}$

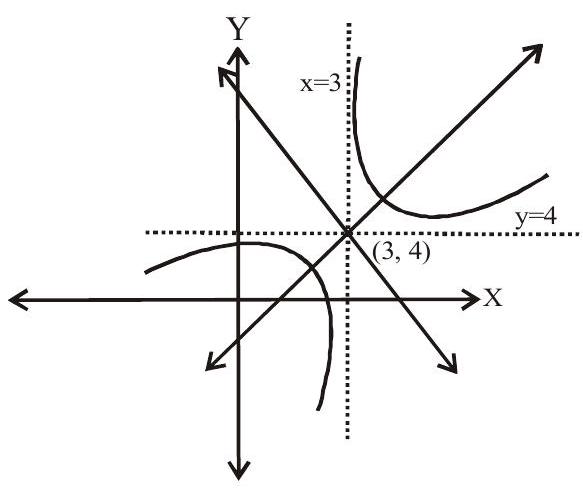
Answer: (a)

2. If $S_1$ and $S_2$ are the foci of the hyperbola whose transverse axis length is 4 and conjugate axis length is $6,S_3$ and ${\mathrm{S}}_4$ are the foci of the conjugate hyperbola, then the area of the quadrilateral ${\mathrm{S}}_1{\mathrm{S}}_3{\mathrm{S}}_2{\mathrm{S}}_4$ is

(a) 156

(b) 36

(c) 26

(d) None of these

Show Answer

Solution :

${\mathrm{S}}_1{\mathrm{S}}_3{\mathrm{S}}_2{\mathrm{S}}_4$ forms a square.

So required area $=4\times$ area of ${}_{\mathrm{\Delta }}{\mathrm{S}}_1{\mathrm{OS}}_3=4\times \frac{1}{2}$ ae $\times {\mathrm{be}}_1$

$\begin{array}{rl}& =2{\mathrm{abee}}_1=2.2.3.\mathrm{e}{\mathrm{e}}_1\\ & =12{\mathrm{ee}}_1\end{array}$

Now e $=\sqrt{1+\frac{9}{4}}=\frac{\sqrt{13}}{2}\mathrm{\&}{\mathrm{e}}_1=\sqrt{1+\frac{9}{4}}=\frac{\sqrt{13}}{2}$

Hence area $=12\times \frac{\sqrt{13}}{2}\times \frac{\sqrt{13}}{2}=26$ sq.units

Answer: (c)

3. The ellipse $4x^2+9y^2=36$ and the hyperbola $a^2{x}^2-y^2=4$ intersect at right angles then the equation of the circle through the points of intersection of two conic is

(a) $x^2+y^2=25$

(c) $5(x^2+y^2)-3x-4y=0$

(b) $5(x^2+y^2)+3x+4y=0$

(d) $(x^2+y^2)=5$

Show Answer

Solution:

Since ellipse and hyperbola intersect orthogonally, they are confocal.

$\mathrm{e}=\sqrt{1-\frac{4}{9}}=\frac{\sqrt{5}}{3}$

foci of ellipse $(\pm \sqrt{5},0)$

$(a{)}^2=a^2+b^2$

$5=\frac{4}{a^2}+4\Rightarrow a=2$

Let point of intersection in the first quadrant be $\mathrm{P}({\mathrm{x}}_1,{\mathrm{y}}_1)$.

$\mathrm{P}$ lies on both the curves.

$4x_1^2+9y_1^2=36\text{ and }4x_1^2-y_1^2=4$

Adding these two, we get $8{\mathrm{x}}_1{}^2+8{\mathrm{y}}_1{}^2=40$

${\mathrm{x}}_1^2+{\mathrm{y}}_1^2=5$

Equation of circle is $x^2+y^2=5$

4. If $\mathrm{e}$ is the eccentricity of the hyperbola $\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}-\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$ and $2\theta$ is angle between the asymptotes then $\cos \theta =$

(a) $\frac{1}{\mathrm{e}}$

(b) $\frac{1-e}{e}$

(c) $\frac{1+\mathrm{e}}{\mathrm{e}}$

(d) None of these

5. From a point $p(1,2)$ pair of tangents are drawn to a hyperbola in which one tangent to each arm of hyperbola. Equation of asymptotes of hyperbola are $\sqrt{3}x-y+5=0$ and $\sqrt{3}x+y-1=0$ then eccentricity of hyperbola is

(a) $\sqrt{3}$

(b) $\frac{2}{\sqrt{3}}$

(c) $2$

(d) None of these

Show Answer

Solution:

Equation of asymptotes are

$\sqrt{3}\mathrm{x}-\mathrm{y}+5=0$

$-\sqrt{3}\mathrm{x}-\mathrm{y}+1=0$

$\therefore {\mathrm{a}}_1{\mathrm{a}}_2+{\mathrm{b}}_1{\mathrm{b}}_2=-3+1<0$

$\therefore$ origin lies in acute angle and $\mathrm{P}(1,2)$ lies in obtuse angle.

$\therefore \mathrm{e}=\sec \theta$ where $2\theta$ is the angle between asymptotes.

$2\theta =\frac{\pi }{3}\Rightarrow \theta =\frac{\pi }{6}$

$\mathrm{e}=\sec \frac{\pi }{6}=\frac{2}{\sqrt{3}}$

Answer: (b)

6. If a variable line has its intercepts on the coordinate axes $\mathrm{e},{\mathrm{e}}^{\prime }$ where $\frac{\mathrm{e}}{2},\frac{{\mathrm{e}}^{\prime }}{2}$ are the eccentricities of a hyperbola and its conjugate hyperbola, then the line always touches the circle ${\mathrm{x}}^2+{\mathrm{y}}^2={\mathrm{r}}^2$, where $\mathrm{r}=$

(a) $4$

(b) $3$

(c) $2$

(d) Can not be decided

7. If angle between asymptotes of hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ is ${120}^{\circ }$ and product of perpendiculars drawn from foci upon its any tangent is 9 , then locus of point of intersection of perpendicular tangents of the hyperbola can be

(a) $x^2+y^2=18$

(b) ${\mathrm{x}}^2+{\mathrm{y}}^2=6$

(c) ${\mathrm{x}}^2+{\mathrm{y}}^2=9$

(d) ${\mathrm{x}}^2+{\mathrm{y}}^2=3$

8. The equation of the transverse axis of the hyperbola

$(x-3{)}^2+(y+1{)}^2=(4x+3y{)}^2$ is

(a) $3x-4y=0$

(b) $4x+3y=0$

(c) $3x-4y=13$

(d) $4x+3y=9$

Practice questions

1. The equation of common tangents to the parabola $y^2=8x$ and hyperbola $3x^2-y^2=3$ is

(a) $x\pm 2y-1=0$

(b) $x\pm 2y+1=0$

(c) $2\mathrm{x}\pm \mathrm{y}+1=0$

(d) $2\mathrm{x}\pm \mathrm{y}-1=0$

2. A tangent to the hyperbola $y=\frac{x+9}{x+5}$ passing through the origin is

(a) $x-2y=0$

(b) $5x-y=0$

(c) $5\mathrm{x}+\mathrm{y}=0$

(d) $x+225y=0$

3. The equation of the common tangent to the curves $y^2=8x$ and $xy=-1$ is

(a) $y=x+2$

(b) $y=2x+1$

(c) $2y=x+8$

(d) $3y=9x+2$

4. Let $\mathrm{PQ}$ be a double ordinate of the hyperbola $\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}-\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$. If $\mathrm{O}$ be the centre of the hyperbola and $\mathrm{OPQ}$ is an equilateral triangle, then eccentricity e is

(a) $>\sqrt{3}$

(b) $>2$

(c) $>\frac{2}{\sqrt{3}}$

(d) None of these

5. The difference between the length $2\mathrm{a}$ of the transverse axis of a hyperbola of eccentricity e and the length of its latus rectum is

(a) $\mathrm{a}(2{\mathrm{e}}^2-1)$

(b) $2\mathrm{a}({\mathrm{e}}^2-1)$

(c) $2\mathrm{a}|3-{\mathrm{e}}^2|$

(d) $2\mathrm{a}|2-{\mathrm{e}}^2|$

6. The slopes of common tangents to the hyperbolas $\frac{{\mathrm{x}}^2}{9}-\frac{{\mathrm{y}}^2}{16}=1$ and $\frac{{\mathrm{y}}^2}{9}-\frac{{\mathrm{x}}^2}{16}=1$ are

(a) $\pm 2$

(b) $\pm \sqrt{2}$

(c) $\pm 1$

(d) None of these

7. The two conics $\frac{y^2}{b^2}-\frac{x^2}{a^2}=1$ and $y^2=-\frac{b}{a}x$ intersect if $f$

(a) $0<\mathrm{b}\le \frac{1}{2}$

(b) $0<\mathrm{a}\le \frac{1}{2}$

(c) b ${}^2<{\mathrm{a}}^2$

(d) $b^2>a^2$

8. The point on the hyperbola $\frac{x^2}{24}-\frac{y^2}{18}=1$ which is nearest to the line $3x+2y+1=0$ is

(a) $(-6,3)$

(b) $(3,-6)$

(c) $(-6,-3)$

(d) $(6,3)$

9. If $(\mathrm{asec}\theta ,b\tan \theta )$ and $(\mathrm{asec}\varphi ,b\tan \varphi )$ be the coordinates of the ends of a focal chord of the hyperbola $\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}-\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$, then $\tan \frac{\theta }{2}\tan \frac{\varphi }{2}=$

(a) $\frac{1+\mathrm{e}}{1-\mathrm{e}}$

(b) $\frac{1-\mathrm{e}}{1+\mathrm{e}}$

(c) $\frac{\mathrm{e}-1}{\mathrm{e}+1}$

(d) None of these

10. If the latus rectum of a hyperbola through one focus subtends ${60}^{\circ }$ angle at the other focus, then its eccentricity e is

(a) $\sqrt{2}$

(b) $\sqrt{3}$

(c) $\sqrt{5}$

(d) $\sqrt{6}$