HYPERBOLA- 7 (Rectangular Hyperbola)
Rectangular Hyperbola
A hyperbola whose asymptotes include a right angle is said to be rectangular hyperbola.
OR
If the lengths of transverse and conjugate axes of any hyperbola be equal it is called rectangular or equilateral hyperbola.
According to first definition
then
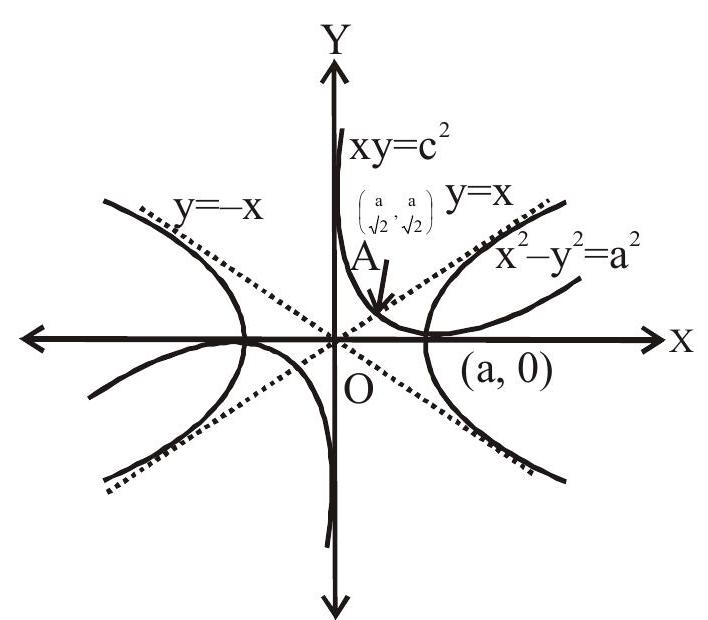
According to second definition
When
Eccentricity
Then asymptotes of
Now equation of asymptotes of new hyperbola is
Then equation of hyperbola is
The hyperbola passes through the point
Then equation of hyperbola is
If the asymptotes of a rectangular hyperbola are
1. Asymptotes :
2. Transverse axis:
Conjugate axis :
3. Vertices
4. Foci :
5. Length of transverse axis
6. Equation of auxiliary circle
7. Equation of director circle
8.
Properties of Rectangular Hyperbola
1. Eccentricity of rectangular hyperbola is
2. Since
3. Equation of chord joining
4. Equation of tangent at
5. Equation of tangent at is
6. Equation of normal at
Equation of normal at is
7. Point of intersection of tangents at
8. Point of intersection of normal at
Examples
1. If the normal at the point
(a)
(b)
(c)
(d)
Show Answer
Solution:
Equation of normal at
But this passes through
Answer: (b)
2. A triangle has its vertices on a rectangular hyperbola
The orthocenter of the triangle lies on
(a)
(b)
(c)
(d) None of these
Show Answer
Solution:
Let
Now slope of
Hence slope of
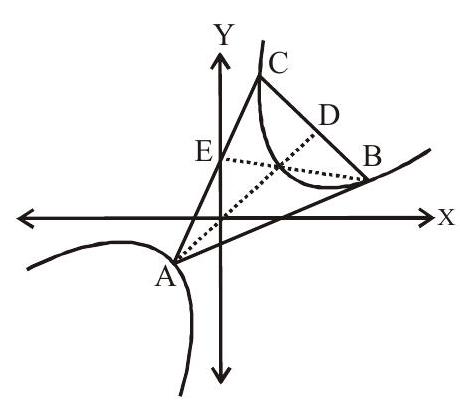 Equation of
Equation of Similarly
slope of
Equation of
Solving (1) and (2) we get
Which satisfies
Therefore orthocentre lies on
Answer: (c)
3. If
(a)
(b)
(c)
Show Answer
Solution:
Let

Answer: (a)
4.
(a)
(b)
(c)
(d)
Show Answer
Solution:
Let coordinates of P, Q, R, S be
Now PQ
Now slope of
Similarly slope of
Similarly slope of
Similarly slope of
Product of their slopes
Answer: (c)
5. The angle between the rectangular hyperbolas
(a)
(b)
(c)
(d)
Show Answer
Solution:
For another hyperbola
Now
Answer: (a)
6. The family of the curves which intersect the family of rectangular hyperbola
(a) family of circle
(b) family of parabola
(c) family of ellipse
(d) family of hyperbola
Show Answer
Solution:
Differentiate w.r.t.
Replace
family of hyperbola.
Answer: (d)
Practice questions
1. The coordinates of the foci of the rectangular hyperbola
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)2. The equation of directories of the rectangular hyperbola
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)3. If the line
(a)
(b)
(c)
(d)
Show Answer
Answer: (c, d)4. Consider the set of hyperbolas
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)5. If chords of the hyperbola
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)6. If the tangent and normal to a rectangular hyperbola
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)7. The points of intersection of the cranes whose parametric equations are
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)8. Number of maximum tangents from any point to the hyperbola
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)9. The length of the latus rectum of the hyperbola
(a)
(b)
(c)
(d) None of these
Show Answer
Answer: (b)10. If
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)11. The equation of the chord joining two points
(a)
(b)
(c)
(d)










