SATHEE: HYPERBOLA- 6 (Asymptotes)

HYPERBOLA- 6 (Asymptotes)

Equation of Chord of Contact

Let equation of hyperbola be $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ ,

Equation of Chord of contact is

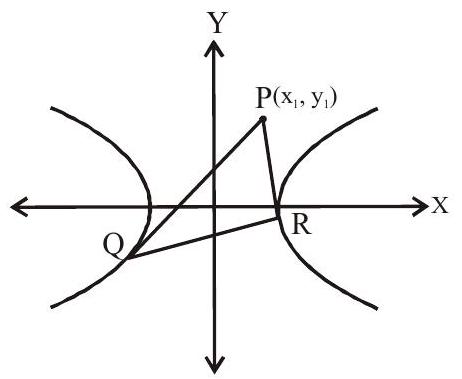
$\begin{array}{ll} \frac{{xx}_{1}}{a^{2}} - \frac{{yy}_{1}}{b^{2}} - 1 = 0 \\ or T = 0 \\ where T = \frac{{xx}_{1}}{a^{2}} - \frac{{yy}_{1}}{b^{2}} - 1 \end{array}$

Example 1: If tangents of the parabola $y^{2} = 4 a x$ intersect the hyperbola $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ at $P$ and $Q$ , then locus of point of intersection of tangents at $P$ and $Q$ is

(a). $a^{3} y^{2} + b^{4} x^{2} = 0$

(b). $a^{3} y^{2} + b^{4} x = 0$

(c). $a^{2} y^{2} + b^{2} x^{2} = 0$

(d). none of these

Show Answer

Solution :

Let $P_{1} (h, k)$ be the point of intersections of tangents at $P$ and $Q$ . Therefore, the equation of chord of contact PQ is

$\begin{aligned} \frac{x h}{a^{2}} - \frac{y k}{b^{2}} = 1 \\ y = \frac{x b^{2} h}{a^{2} k} - \frac{b^{2}}{k} which touches the parabola y^{2} = 4 a x \\ ∴ - \frac{b^{2}}{k} = \frac{a}{(\frac{b^{2} h}{a^{2} k})} \\ - \frac{b^{2}}{k} = \frac{a^{3} k}{b^{2} h} \\ ∴ Locus of (h, k) is y^{2} = - \frac{b^{4}}{a^{3}} x \end{aligned}$

$a^{3} y^{2} + b^{4} x = 0$

Answer: (b)

Equation of the chord of the hyperbola whose mid point is given

$A$ is the mid point of $PQ$ , then equation of chord is

$\frac{{xx}_{1}}{a^{2}} - \frac{{yy}_{1}}{b^{2}} = \frac{x_{1}^{2}}{a^{2}} - \frac{y_{1}^{2}}{b^{2}}$

ie. $T = S_{1}$ where

$T = \frac{{xx}_{1}}{a^{2}} - \frac{{yy}_{1}}{b^{2}} - 1$

$S_{1} = \frac{x_{1}^{2}}{a^{2}} - \frac{y_{1}^{2}}{b^{2}} - 1$

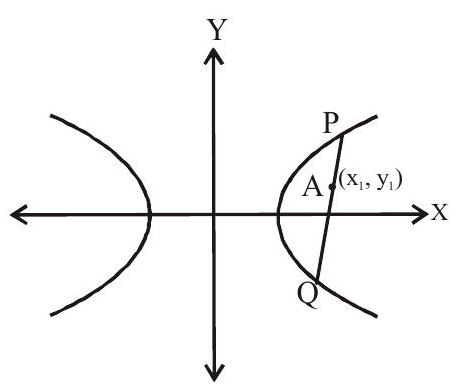
Example 2: The locus of the middle points of the chord of hyperbola $3 x^{2} - 2 y^{2} + 4 x - 6 y = 0$ parallel to $y = 2 x$ is

(a). $3 x + 4 y = 4$

(b). $4 x + 3 y = 12$

(c). $3 x - 4 y = 4$

(d). none of these

Show Answer

Solution :

Let mid point of the chord be ( $h, k$ ), equation of the chord is $T = S_{1}$ i.e.

$3 xh - 2 yk + 2 (x + h) - 3 (y + k) = 3 h^{2} - 2 k^{2} + 4 h - 6 k$

$\Rightarrow x (3 h + 2) - y (2 k + 3) - 3 h^{2} + 2 k^{2} - 2 h + 3 k = 0$

Its slope is $\frac{3 h + 2}{2 k + 3} = 2$ (slope of $y = 2 x$ )

$3 h - 4 k = 4$

Locus of $(h, k)$ is $3 x - 4 y = 4$

Answer: (c)

Asymptotes of Hyperbola

An asymptotes of any hyperbola is a straight line which touches in it two points at infinity. OR If the length of the perpendicular let fall from a point on a hyperbola to a straight line tends to zero as the point on the hyperbola moves to infinity along the hyperbola, then the straight line is called asymptote of the hyperbola.

The equation of two asymptotes of the hyparbola $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ are $y = \pm \frac{b}{a} x$ or $\frac{x}{a} \pm \frac{y}{b} = 0$

Pair of asymptotes: $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 0$

1. If $b = a$ , then $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ reduces to $x^{2} - y^{2} = a^{2}$ . The asymptotes of rectangular hyperbola $x^{2} - y^{2} = a^{2}$ are $y = \pm x$ which are at right angles.

2. A hyperbola and its conjugate hyperbola have the same asymptotes.

3. The angle between the asymptotes of $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ is $2 \tan^{- 1} (\frac{b}{a})$

4. The asymptotes pass through the centre of the hyperbol(a).

5. The bisectors of the angle between the asymptotes are the coordinate axes.

6. Let $H = \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} - 1 = 0$

$A = \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 0$

and $C = \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} + 1 = 0$

be the equation of the hyperbola, asymptotes and the conjugate hyperbola respectively, then clearly

$C + H = 2 A$

Example 3: The asymptotes of the hyperbola $x y - 3 y - 2 x = 0$ are

(a). $x - 3 = 0$

(b). $x + y = 0$

(c). $y - 2 = 0$

(d). $x - y = 0$

Show Answer

Solution :

Since equation of a hyperbola and its asymptotes differ in constant terms only. Pair of asymptotes is given by

$x y - 3 y - 2 x + c = 0$

It represents a pair of straight line

$\begin{aligned} ∴ | \begin{array}{ccc} 0 & \frac{1}{2} & - 1 \\ \frac{1}{2} & 0 & \frac{- 3}{2} \\ - 1 & \frac{- 3}{2} & c \end{array} | = 0 \\ - \frac{1}{2} (\frac{c}{2} - \frac{3}{2}) - (- \frac{3}{4}) = 0 \\ - \frac{c}{4} + \frac{3}{4} + \frac{3}{4} = 0 \\ c = 6 \\ ∴ xy - 3 y - 2 x + 6 = 0 \\ (x - 3) (y - 2) = 0 \end{aligned}$

Asymptotes are $x - 3 = 0$ and $y - 2 = 0$

Answer : a, c

Example 4: The equation of the hyperbola which has $3 x - 4 y + 7 = 0$ and $4 x + 3 y + 1 = 0$ as its asymptotes and which passes through the origin is

(a). $x^{2} - y^{2} = 12 x y$

(b). $12 x^{2} - 7 x y - 12 y^{2} + 31 x + 17 y = 0$

(c). $12 x^{2} - 12 y^{2} = 7 x y$

(d). $12 x^{2} + 7 x y - 12 y^{2} + 25 x - 19 y = 0$

Show Answer

Solution :

Combined equation of the asymptotes is

$\begin{aligned} (3 x - 4 y + 7) (4 x + 3 y + 1) = 0 \\ 12 x^{2} - 7 x y - 12 y^{2} + 31 x + 17 y + 7 = 0 \end{aligned}$

Since equation of hyperbola and combined equation of its asymptotes differ by a constant, therefore equation of hyperola may be

$12 x^{2} - 7 x y - 12 y^{2} + 31 x + 17 y + c = 0$

But it passes through the origin. $So c = 0$

Hence equation of hyperbola is

$12 x^{2} - 7 x y - 12 y^{2} + 31 x + 17 y = 0$

Answer: (b)

Example 5: The product of the lengths of perpendiculars drawn from any point on the hyperbola $x^{2} - 2 y^{2} = 2$ to its asymptotes is

(a). $\frac{3}{2}$

(b). $1$

(c). $2$

(d). $\frac{2}{3}$

Show Answer

Solution :

Given hyperbola is

$\frac{x^{2}}{2} - \frac{y^{2}}{1} = 1$

Let $P (\sqrt{2} \sec θ, \tan θ)$ a point on the hyperbol(a).

Equation of asymptotes is $\frac{x}{\sqrt{2}} - y = 0$ and $\frac{x}{\sqrt{2}} + y = 0$

Product of the lengths of perpendiculars $= \frac{(\sec θ - \tan θ)}{\sqrt{\frac{1}{2} + 1}} \cdot \frac{(\sec θ + \tan θ)}{\sqrt{\frac{1}{2} + 1}}$

$= \frac{\sec^{2} θ - \tan^{2} θ}{\frac{3}{2}}$

$= \frac{2}{3}$

Answer: (d)

Example: 6 The angle between the asymptotes of the hyperbola

$\frac{x^{2}}{16} - \frac{y^{2}}{9} = 1$

(a). $\tan^{- 1} (\frac{3}{4})$

(b). $\tan^{- 1} (\frac{24}{7})$

(c). $2 \tan^{- 1} (\frac{4}{3})$

(d). $2 \tan^{- 1} (\frac{4}{5})$

Show Answer

Solution :

Equations of asymptotes are $\frac{x}{4} - \frac{y}{3} = 0$ and $\frac{x}{4} + \frac{y}{3} = 0$

slope of first asymptote is $\tan θ = \frac{3}{4}$

$θ = \tan^{- 1} (\frac{3}{4})$

Angle between the asymptotes is $2 θ = 2 \tan^{- 1} (\frac{3}{4})$

$\begin{aligned} = \tan^{- 1} (\frac{2 \times \frac{3}{4}}{1 - \frac{9}{16}}) \\ = \tan^{- 1} (\frac{24}{7}) \end{aligned}$

Answer: (b)

Practice questions

1. If angle between asymptotes of hyperbola $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ is $120^{\circ}$ and product of perpendiculars drawn from foci upon its any tangent is 9 , then locus of point of intersection of perpendicular tangents of the hyperbola can be

(a). $x^{2} + y^{2} = 6$

(b). $x^{2} + y^{2} = 9$

(c). $x^{2} + y^{2} = 3$

(d). $x^{2} + y^{2} = 18$

Show Answer

Answer: (d)

2. For a hyperbola whose centre is at $(1, 2)$ and asymptotes are parallel to lines $2 x + 3 y = 0$ and $x + 2 y = 1$ , then equation of hyperbola passing through $(2, 4)$ is

(a). $(2 x + 3 y - 5) (x + 2 y - 8) = 40$

(b). $(2 x + 3 y - 8) (x + 2 y - 5) = 40$

(c). $(2 x + 3 y - 8) (x + 2 y - 5) = 30$

(d). none of these

Show Answer

Answer: (b)

3. Asymptotes of the hyperbola $\frac{x^{2}}{a_{1}^{2}} - \frac{y^{2}}{b_{1}^{2}} = 1$ and $\frac{x^{2}}{a_{2}^{2}} - \frac{y^{2}}{b_{2}^{2}} = 1$ are perpendicular to each other then,

(a). $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}$

(b). $a_{1} a_{2} = b_{1} b_{2}$

(c). $a_{1} - a_{2} = b_{1} - b_{2}$

(d). $a_{1} a_{2} + b_{1} b_{2} = 0$

Show Answer

Answer: (d)

4. If $S = 0$ be the equation of the hyperbola $x^{2} + 4 x y + 3 y^{2} - 4 x + 2 y + 1 = 0$ , then the value of $k$ for which $S + k = 0$ represents its asymptotes is

(a). $- 22$

(b). $18$

(c). $- 16$

(d). $20$

Show Answer

Answer: (a)

5. A hyperbola passes through $(2, 3)$ and has asymptotes $3 x - 4 y + 5 = 0$ and $12 x + 5 y - 40 = 0$ , then the equation of its transverse axis is

(a). $77 x - 21 y - 265 = 0$

(b). $21 x - 77 y - 265 = 0$

(c). $21 x - 77 y - 265 = 0$

(d). $21 x + 77 y - 265 = 0$

Show Answer

Answer: (d)

6. The combined equation of the asymptotes of the hyperbola $2 x^{2} + 5 x y + 2 y^{2} + 4 x + 5 y = 0$ is

(a). $2 x^{2} + 5 x y + 2 y^{2} + 7 = 0$

(c). $2 x^{2} + 5 x y + 2 y^{2} + 4 x + 5 y + 2 = 0$

(b). $2 x^{2} + 5 x y + 2 y^{2} + 4 x + 5 y + 7 = 0$

(d). None of these

Show Answer

Answer: (c)

7. The asymptotes of the hyperbola $x y + h x + k y = 0$ are

(a). $x + h = 0$ and $y + k = 0$

(b). $x + h = 0$ and $y - k = 0$

(b). $x + k = 0$ and $y + h = 0$

(c). $x - k = 0$ and $y - h = 0$

Show Answer

Answer: (c)

8. If foci of hyperbola lie on $y = x$ and one of the asymptote is $y = 2 x$ , then equation of the hyperbola, given that it passes through $(5, 4)$ is

(a). $2 x^{2} - 2 y + 5 x y + 5 = 0$

(b). $2 x^{2} + 2 y^{2} - 5 x y + 10 = 0$

(c). $x^{2} - y^{2} - x y + 5 = 0$

(d). None of these

Show Answer

Answer: (b)

Linked comprehension type (for problems 9 - 11)

In hyperbola portion of tangent intercept between asymptotes is bisected at the point of contact. Consider a hyperbola whose centre is at origin. A line $x + y = 2$ touches this hyperbola at $P (1, 1)$ and intersects the asymptotes at $A$ and $B$ such that $A B = 6 \sqrt{2}$ units.

9. Equation of asymptotes are

(a). $2 x^{2} + 2 y^{2} - 5 x y = 0$

(b). $2 x^{2} + 5 x y + 2 y^{2} = 0$

(c). $3 x^{2} + 6 x y + 4 y^{2} = 0$

(d). None of these

Show Answer

Answer: (b)

10. Equation of tangent to the hyperbola at $(- 1, \frac{7}{2})$ is

(a). $3 x + 2 y = 4$

(b). $3 x + 4 y = 11$

(c). $5 x + 2 y = 2$

(d). none of these

Show Answer

Answer: (a)

11. Angle subtended by $A B$ at centre of the hyperbola is

(a). $\tan^{- 1} (\frac{4}{3})$

(b). $\tan^{- 1} (\frac{2}{3})$

(c). $\tan^{- 1} (\frac{3}{4})$

(d). none of these

Show Answer

Answer: (c)

Hyperbola

HYPERBOLA- 6 (Asymptotes)

Equation of Chord of Contact

Equation of the chord of the hyperbola whose mid point is given

Asymptotes of Hyperbola

Practice questions

Linked comprehension type (for problems 9 - 11)

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Mentorship

NCERT Exercise Video Solution

Hyperbola

HYPERBOLA- 6 (Asymptotes)

Equation of Chord of Contact

Equation of the chord of the hyperbola whose mid point is given

Asymptotes of Hyperbola

Practice questions

Linked comprehension type (for problems 9 - 11)

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Mentorship

NCERT Exercise Video Solution

Menu