HYPERBOLA- 5 (Normals)
Equation of Pair of Tangents
Let equation of hyperbola be $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ and a point $\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ then the combined equation of tangents $\mathrm{PA}$ and $\mathrm{PB}$ is $\mathrm{SS} _{1}=\mathrm{T}^{2}$ where
$ \begin{aligned} & \mathrm{S}=\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}-1 \\ & \mathrm{~S} _{1}=\frac{\mathrm{x} _{1}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y} _{1}^{2}}{\mathrm{~b}^{2}}-1 \\ & \mathrm{~T}=\frac{\mathrm{xx} _{1}}{\mathrm{a}^{2}}-\frac{\mathrm{yy} _{1}}{\mathrm{~b}^{2}}-1 \end{aligned} $
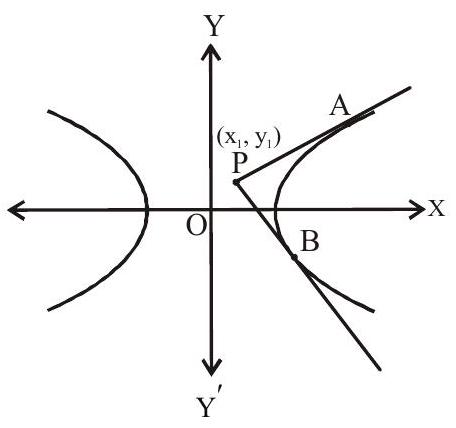
Example 1: A pair of tangents drawn from the point $(4,3)$ to the hyperbola $\frac{x^{2}}{16}-\frac{y^{2}}{9}=1$ then angle between the tangents is
(a). $\tan ^{-1}\left(\frac{3}{4}\right)$
(b). $\frac{\pi}{2}$
(c). $\tan ^{-1}\left(\frac{4}{3}\right)$
(d). $\tan ^{-1}\left(\frac{1}{2}\right)$
Show Answer
Solution :
$\mathrm{S}=\frac{\mathrm{x}^{2}}{16}-\frac{\mathrm{y}^{2}}{9}-1, \mathrm{~S} _{1}=\frac{16}{16}-\frac{9}{9}-1=-1, \mathrm{~T}=\frac{4 \mathrm{x}}{16}-\frac{3 \mathrm{y}}{9}-1$
Equation of pair of tangents is $\mathrm{SS} _{1}=\mathrm{T}^{2}$
$ \begin{aligned} & -1\left(\frac{x^{2}}{16}-\frac{y^{2}}{9}-1\right)=\left(\frac{x}{4}-\frac{y}{3}-1\right)^{2} \\ & -\frac{x^{2}}{16}+\frac{y^{2}}{9}+1=\frac{x^{2}}{16}+\frac{y^{2}}{9}+1-\frac{x y}{6}-\frac{x}{2}+\frac{2 y}{3} \\ & 3 x^{2}-4 x y-12 x+16 y=0 \\ & 3 x-4 y=0, x-4=0 \\ & m _{1}=\frac{3}{4} m _{2}=\infty \\ & \theta=\frac{\pi}{2}-\tan ^{-1} \frac{3}{4}=\cot ^{-1} \frac{3}{4}=\tan ^{-1} \frac{4}{3} \end{aligned} $
Answer: (c)
Equation of Normal to the Hyperbla :
i. Point Form
$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$
Slope to tangent $=+\frac{b^{2} x _{1}}{a^{2} y _{1}}$
Slope to normal $=-\frac{a^{2} y _{1}}{b^{2} x _{1}}$
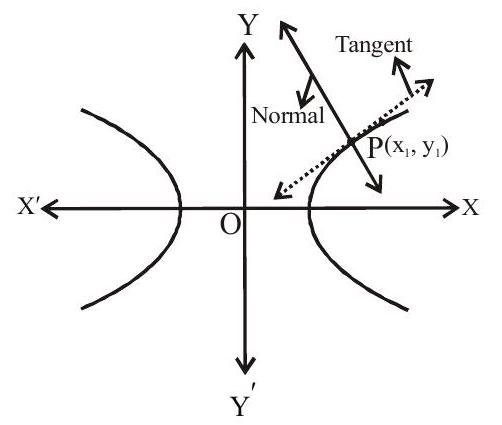
Equation of normal $y-y _{1}=-\frac{a^{2} y _{1}}{b^{2} x _{1}}\left(x-x _{1}\right)$
$\frac{\mathrm{a}^{2} \mathrm{x}}{\mathrm{x} _{1}}+\frac{\mathrm{b}^{2} \mathrm{y}}{\mathrm{y} _{1}}=\mathrm{a}^{2}+\mathrm{b}^{2}$
ii. Parametric Form
$\mathrm{P}( a \sec \theta, b \tan \theta)$
$ \frac{\mathrm{ax}}{\sec \theta}+\frac{\mathrm{by}}{\tan \theta}=a^{2}+\mathrm{b}^{2} $
or $a x \cos \theta+b y \cot \theta=a^{2}+b^{2}$
iii. Slope Form:
$y=m x \pm \frac{m\left(a^{2}+b^{2}\right)}{\sqrt{a^{2}-m^{2} b^{2}}}$
Point of contanct is $\left( \pm \frac{a^{2}}{\sqrt{a^{2}-m^{2} b^{2}}}, \mp \frac{m b^{2}}{\sqrt{a^{2}-m^{2} b^{2}}}\right)$
Exercises
1. A normal to the hyperbola $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ meets the axes in $\mathrm{M}$ and $\mathrm{N}$ and lines MP and NP are drawn perpendiculars to the axes meeting at $\mathrm{P}$. The locus of $\mathrm{P}$ is
(a). $a^{2} x^{2}-b^{2} y^{2}=\left(a^{2}+b^{2}\right)^{2}$
(b). $a^{2} x^{2}-b^{2} y^{2}=a^{2}+b^{2}$
(c). $b^{2} x^{2}-a^{2} y^{2}=a^{2}+b^{2}$
(d). $a^{2} x^{2}-b^{2} y^{2}=a^{2}-b^{2}$
Show Answer
Solution :
Equation of normal is $a x \cos \theta+b y \cot \theta=a^{2}+b^{2}$
Normat meets the axes at $\mathrm{M}\left(\frac{\mathrm{a}^{2}+\mathrm{b}^{2}}{\mathrm{a} \cos \theta}, 0\right)$ and $\mathrm{N}\left(0, \frac{\mathrm{a}^{2}+\mathrm{b}^{2}}{\mathrm{~b} \cot \theta}\right)$
Now equation of PM is $x=\frac{a^{2}+b^{2}}{a \cos \theta}$
$ \Rightarrow \sec \theta=\frac{a x}{a^{2}+b^{2}} $
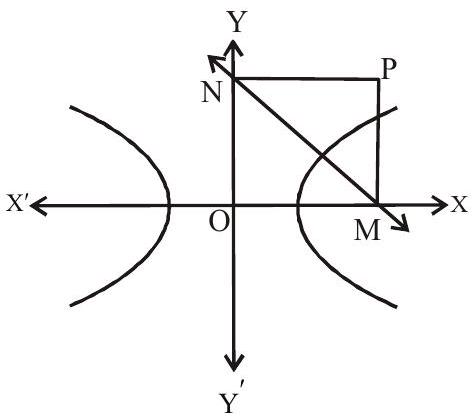
and equation of $P N$ is $y=\frac{a^{2}+b^{2}}{b \cot \theta}$
$ \begin{aligned} & \Rightarrow \tan \theta=\frac{\text { by }}{a^{2}+b^{2}} \\ & \sec ^{2} \theta-\tan ^{2} \theta=1 \end{aligned} $
$ \begin{aligned} & \frac{a^{2} x^{2}}{\left(a^{2}+b^{2}\right)^{2}}-\frac{b^{2} y^{2}}{\left(a^{2}+b^{2}\right)^{2}}=1 \\ & \therefore a^{2} x^{2}-b^{2} y^{2}=\left(a^{2}+b^{2}\right)^{2} \end{aligned} $
Answer: (a)
2. The line $1 \mathrm{x}+\mathrm{my}-\mathrm{n}=0$ will be normal to the hyperbola $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ if
(a). $1^{2} \mathrm{a}^{2}+\mathrm{b}^{2} \mathrm{~m}^{2}=\frac{\left(\mathrm{a}^{2}+\mathrm{b}^{2}\right)}{\mathrm{n}}$
(b). $\frac{\mathrm{a}^{2}}{1^{2}}+\frac{\mathrm{b}^{2}}{\mathrm{~m}^{2}}=\frac{\left(\mathrm{a}^{2}+\mathrm{b}^{2}\right)^{2}}{\mathrm{n}^{2}}$
(c). $\frac{\mathrm{a}^{2}}{\mathrm{l}^{2}}-\frac{\mathrm{b}^{2}}{\mathrm{~m}^{2}}=\frac{\left(\mathrm{a}^{2}+\mathrm{b}^{2}\right)^{2}}{\mathrm{n}^{2}}$
(d). $\frac{a^{2}}{1^{2}}-\frac{b^{2}}{m^{2}}=\frac{a^{2}+b^{2}}{n^{2}}$
Show Answer
Solution :
Equation of normal is ax $\cos \theta+b y \cot \theta=a^{2}+b^{2}$
This equation compare with $1 \mathrm{x}+\mathrm{my}=\mathrm{n}$
i.e. $\frac{a \cos \theta}{1}=\frac{b \cot \theta}{m}=\frac{a^{2}+b^{2}}{n}$
$\Rightarrow \sec \theta=\frac{\mathrm{an}}{1\left(\mathrm{a}^{2}+\mathrm{b}^{2}\right)}$
$\Rightarrow \tan \theta=\frac{\mathrm{bn}}{\mathrm{m}\left(\mathrm{a}^{2}+\mathrm{b}^{2}\right)}$
$\therefore \sec ^{2} \theta-\tan ^{2} \theta=1$
$\frac{\mathrm{a}^{2}}{\mathrm{l}^{2}}-\frac{\mathrm{b}^{2}}{\mathrm{~m}^{2}}=\frac{\left(\mathrm{a}^{2}+\mathrm{b}^{2}\right)^{2}}{\mathrm{n}^{2}}$
Answer: (c)
3. The line $x \cos \alpha+y \sin \alpha=p$ touches the hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ if
(a). $ a^{2} \cos ^{2} \alpha+b^{2} \sin ^{2} \alpha=p$
(b). $ a^{2} \cos ^{2} \alpha-b^{2} \sin ^{2} \alpha=p^{2}$
(c). $ a^{2} \cos ^{2} \alpha+b^{2} \sin ^{2} \alpha=p^{2}$
(d). $ a^{2} \cos ^{2} \alpha-b^{2} \sin ^{2} \alpha=p$
Show Answer
Solution :
The line $y=m x+c$ touches the hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$, then $c^{2}=a^{2} m^{2}-b^{2}$
Given equation is $\mathrm{y}=-\cot \alpha+\mathrm{p} \operatorname{cosec} \alpha \mathrm{y}=-\mathrm{x} \cot \alpha+\mathrm{p} \operatorname{cosec}$
$\therefore \mathrm{p}^{2} \operatorname{cosec}^{2} \alpha=\mathrm{a}^{2}(-\cot \alpha)^{2}-\mathrm{b}^{2}$
$\mathrm{p}^{2}=\mathrm{a}^{2} \cos ^{2} \alpha-\mathrm{b}^{2} \sin ^{2} \alpha$
Answer: (b)
4. The normal at $\mathrm{P}$ to a hyperbola of eccentricity e, intersects its transverse and conjugate axes at L and $\mathrm{M}$ respectiely. The locus of the mid point of LM is a hyperbola then eccentricity of the hyperbola is
(a). $\frac{\mathrm{e}+1}{\mathrm{e}-1}$
(b). $\frac{\mathrm{e}}{\sqrt{\mathrm{e}^{2}-1}}$
(c). $e$
(d). none of these
Show Answer
Solution :
The equation of the normal at $P(\operatorname{asec} \theta, b \tan \theta)$ of the hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ is $a x \cos \theta+b y \cot \theta=a^{2}+b^{2}$
This intersect the transverse and conjugate axes at $\mathrm{L}\left(\frac{\mathrm{a}^{2}+\mathrm{b}^{2}}{\mathrm{a}} \sec \theta, 0\right)$ and $\mathrm{M}\left(0, \frac{\mathrm{a}^{2}+\mathrm{b}^{2}}{\mathrm{~b}} \tan \theta\right)$ respectively.
Let $N(h, k)$ be the mid point of LM, then
$ \begin{aligned} & \mathrm{h}=\frac{\mathrm{a}^{2}+\mathrm{b}^{2}}{2 \mathrm{a}} \sec \theta \text { and } \mathrm{k}=\frac{\mathrm{a}^{2}+\mathrm{b}^{2}}{2 \mathrm{~b}} \tan \theta \\ & \Rightarrow \sec \theta=\frac{2 \mathrm{ah}}{\mathrm{a}^{2}+\mathrm{b}^{2}} \text { and } \tan \theta=\frac{2 \mathrm{~kb}}{\mathrm{a}^{2}+\mathrm{b}^{2}} \\ & \therefore \sec ^{2} \theta-\tan ^{2} \theta=1 \\ & \Rightarrow 4 \mathrm{a}^{2} \mathrm{~h}^{2}-4 \mathrm{~b}^{2} \mathrm{k}^{2}=\left(\mathrm{a}^{2}+\mathrm{b}^{2}\right)^{2} \end{aligned} $
Thus locus of $(h, k)$ is $4 a^{2} x^{2}-4 b^{2} y^{2}=\left(a^{2}+b^{2}\right)^{2}$
Let $\mathrm{e} _{1}$ be the eccentricity of this hyperbola. Then
$ \begin{aligned} & \mathrm{e} _{1}^{2}=1+\frac{\mathrm{a}^{2}}{\mathrm{~b}^{2}}=\frac{\mathrm{a}^{2}+\mathrm{b}^{2}}{\mathrm{~b}^{2}}=\frac{\mathrm{a}^{2} \mathrm{e}^{2}}{\mathrm{a}^{2}\left(\mathrm{e}^{2}-1\right)}=\frac{\mathrm{e}^{2}}{\mathrm{e}^{2}-1} \\ & \Rightarrow \mathrm{e} _{1}=\frac{\mathrm{e}}{\sqrt{\mathrm{e}^{2}-1}} \end{aligned} $
Answer: (b)
Some Important Results
1. Normal other than transverse axis never passes through the focus.
2. Locus of the feet of the perpendicular drawn from focus of the hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ upon any tangent is its auxiliary circle i.e. $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}$.
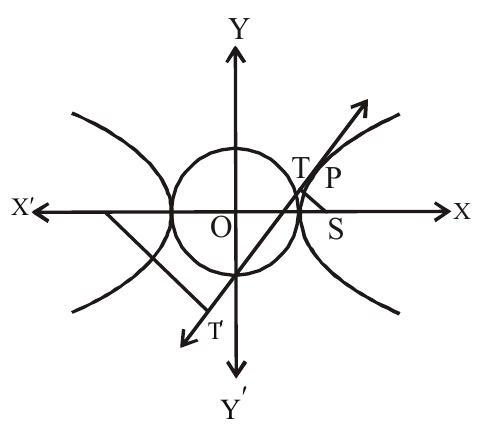
3. The product of the feet of these perpendiculars is $\mathrm{b}^{2}$.
4. The portion of the tangent between the point of contact and the directrix subtends a right angle at the corresponding focus.
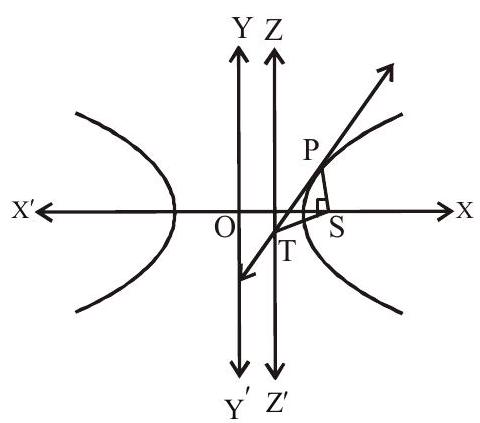
5. The tangent and normal at any point of a hyperbola bisect the angle between the focal radii. This spells the reflection property of the hyperbola as an incoming light ray aimed towards one focus is reflected from the outer surface of the hyperbola towards the other focus.
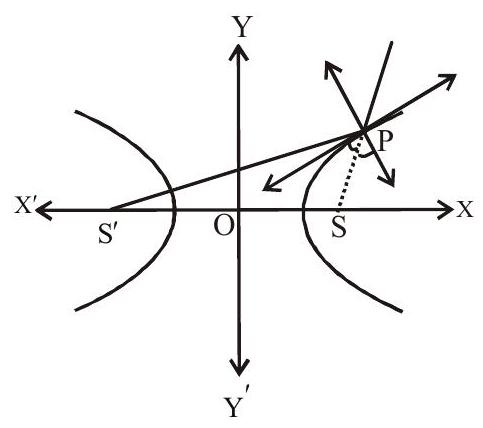
6. If an ellipse and a hyperbola have the same foci, they cut at right anlges at any of their common points.
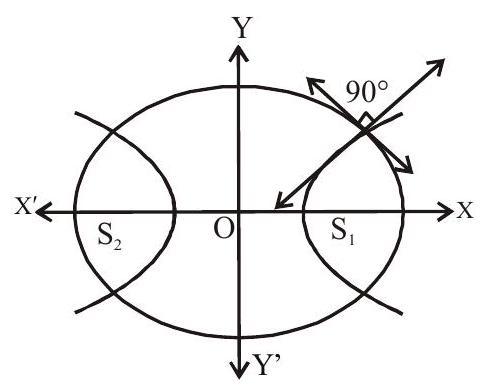
7. The ellipse $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ and the hyperbola $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}-\mathrm{k}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{k}^{2}-\mathrm{b}^{2}}=1(\mathrm{a}>\mathrm{k}>\mathrm{b}>0)$ are confocal and therefore orthogonal.
8. The foci of the hyperbola and the points $\mathrm{P}$ and $\mathrm{Q}$ in which any tangent meets the tangents at the vertices are concyclic with $\mathrm{PQ}$ as diameter of the circle.
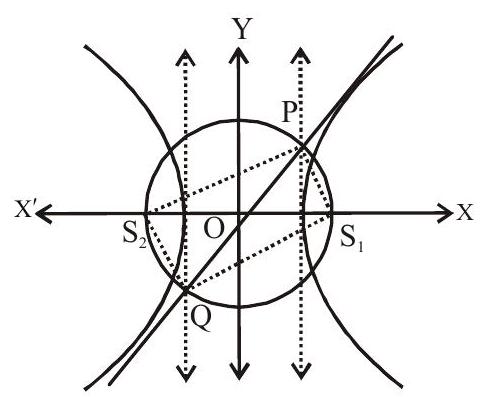
Practice questions
1. Normal is drawn at one of the extremities of the latus rectum of hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$, which meets the axis at points $\mathrm{A}$ and $\mathrm{B}$. Then area of triangle $\mathrm{OAB}(\mathrm{O}$ being the origin) is
(a). $ a^{5} e^{2}$
(b). $ a^{2} e^{5}$
(c). $ \frac{1}{2} \mathrm{a}^{2} \mathrm{e}^{5}$
(d). none of these
Show Answer
Answer: (c)2. If the normal at $P(\theta)$ on the hyperbola $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{2 \mathrm{a}^{2}}=1$ meets the conjugate axis at $\mathrm{G}$ then $\mathrm{AG} \times \mathrm{A}^{\prime} \mathrm{G}$ is (Where $\mathrm{A}$ and $\mathrm{A}^{\prime}$ are the vertices of the hyperbola)
(a). $ a^{2} e^{2} \sec ^{2} \theta-a^{2}$
(b). $ a^{4} e^{2} \sec ^{2} \theta-a^{4}$
(c). $ a^{2} e^{4} \sec ^{2} \theta-a^{2}$
(d). none of these
Show Answer
Answer: (c)3. Normals are drawn to the hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ at points $\theta _{1}$ and $\theta _{2}$ meeting the conjugate axis at $\mathrm{G} _{1}$ and $\mathrm{G} _{2}$ respectively. If $\theta _{1}+\theta _{2}=\frac{\pi}{2}$ then $\mathrm{CG} _{1} \times \mathrm{CG} _{2}$ is (where $\mathrm{C}$ is centre of hyperbola and e is eccentricity of hyperbola)
(a). $\frac{\mathrm{a}^{2} \mathrm{e}^{4}}{\mathrm{e}^{2}-1}$
(b). $\frac{\mathrm{a}^{2} \mathrm{e}^{2}}{\mathrm{e}^{2}-1}$
(c). $\frac{\mathrm{a}^{4} \mathrm{e}^{4}}{\mathrm{e}^{2}-1}$
(d). none of these
Show Answer
Answer: (a)4. Let $\mathrm{P}(a\sec \theta, b \tan \theta)$ and $\mathrm{Q}(a\sec \phi, b \tan \phi)$, where $\theta+\phi=\frac{\pi}{2}$, be two points on the hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$. If $(h, k)$ is the point of intersection of the normals at $P$ and $Q$, then $k$ is equal to
(a). $\frac{a^{2}+b^{2}}{a}$
(b). $-\left(\frac{a^{2}+b^{2}}{a}\right)$
(c). $\frac{\mathrm{a}^{2}+\mathrm{b}^{2}}{\mathrm{~b}}$
(d). $-\left(\frac{a^{2}+b^{2}}{b}\right)$
Show Answer
Answer: (d)5. If the normal at the point $\mathrm{P}$ to the rectangular hyperbola $\mathrm{x}^{2}-\mathrm{y}^{2}=\mathrm{a}^{2}$ meet the axes in $\mathrm{N}$ and $\mathrm{N}^{\prime}$ and $\mathrm{C}(0,0)$ is the centre of the hyperbola then
(a). $\mathrm{PN}=\mathrm{P} \mathrm{N}=\mathrm{PC}$
(b). $\mathrm{PC}=\mathrm{PN} \neq \mathrm{P} \mathrm{N}^{\prime}$
(c). $\mathrm{PN}=\mathrm{P} \mathrm{N} \neq \mathrm{PC}$
(d). none of these
