HYPERBOLA-3 (Equation of Hyperbola)
Equation of a Hyperbola referred to two perpendicular lines
Let equation of hyperbola be
From diagram
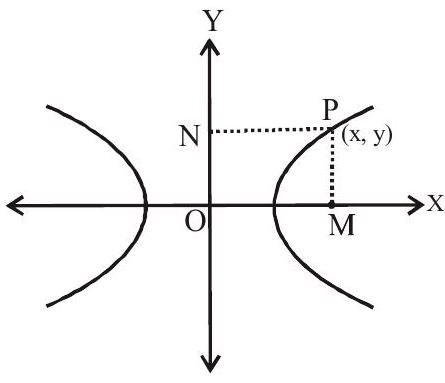
ie. if perpendicular distance of a point
then the locus of point
-
centre of the hyperbola, we get after solving
-
Transverse axis :
-
Conjugate axis
-
Foci : The foci of the hyperbola is the point of intersection of the lines
-
Directrix:
-
Length of transverse axis
-
Length of conjugate axis
-
Length of latus Rectum
Examples
1. Find the eccentricity and centre of the hyperbola
Show Answer
Solution :
2. Find the eccentricity of the conic
Show Answer
Solution :
3. Find the coordinates of the centre, foci and vertices, length of axes and latus rectum, equation of axes and directries, and eccentricity of the conic
Show Answer
Solution :
Let
Centre :
Eccentricity :
Foci :
Vertices :
Length of transverse axis
Length of conjugate axis
Length of latus rectums
Equation of transverse axis :
Equation of conjugate axis :
Equation of directries
4. The equation of the transverse and conjugate axes of a hyperbola are respectively
(a).
(b).
(c).
(d). none of these
Show Answer
Solution :
The equations of hyperbola is
Answer: a
Line and Hyperbola

Let equation of line be
i.
ii.
iii.
Hence
Let this tangent passes through a point
Hence maximum two tangents can be drawn through a point
Now
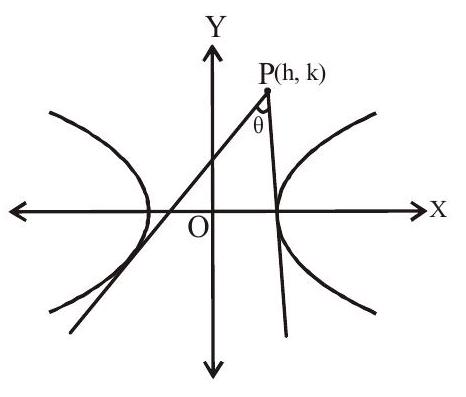
If
If
i.e.
Locus of
Hence, Locus of point of intersection of two perpendicular tangents is known as Director Circle. Its equation is
If
If
For equation of hyperbola
Practice questions
1. If the foci of the ellipse
(a). 3
(b). 5
(c). 7
(d). 9
Show Answer
Answer: (c)2. If
(a).
(b).
(c).
(d).
Show Answer
Answer: (b)3. An ellipse and hyperbola are confocal and the conjugate axis of the hyperbola is equal to the minor axis of the ellipse. If
(a).
(b).
(c).
(d).
Show Answer
Answer: (d)4. The centre of a hyperbola
(a).
(b).
(c).
(d).
Show Answer
Answer: (a)5. The equations of the transverse and conjugate axes of a hyperbola are
(a).
(b).
(c).
(d).
Show Answer
Answer: (c)6. For all real values of
(a).
(b).
(c).
(d).
Show Answer
Answer: (a)7. The equation of tangents to the curve
(a).
(b).
(c).
(d).
Show Answer
Answer: (c)8. If the line
(a).
(b).
(c).
(d).
Show Answer
Answer: (b)9. If
(a).
(b).
(c).
(d).
Show Answer
Answer: (c)10. The locus of the point of intersection of perpendicular tangents to
(a).
(b).
(c).
(d).










