HYPERBOLA-2 (Conjugate Hyperbola)
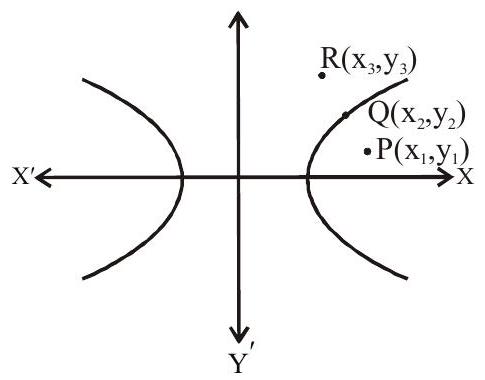
Position of a point
Let a point $\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ and equation of hyperbola be $\frac{\mathrm{x}^{2}}{\mathrm{ya}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}-1=0$
$\mathrm{S} _{1}=\frac{\mathrm{x} _{1}{ }^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y} _{1}{ }^{2}}{\mathrm{~b}^{2}}-1$
If $\mathrm{S} _{1}>0$, point is inside the hyperbola.
If $S _{1}=0$, point is on the hyperbola.
If $\mathrm{S} _{1}<0$, point is outside the hyperbola.
Conjugate Hyperbola
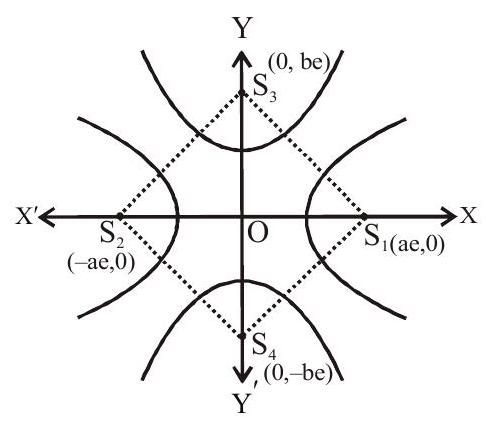
Corresponding to every hyperbola there exists a hyperbola such that the transverse axis and conjugate axis of one is equal to the conjugate axis and transverse axis of the other. Such hyperbolas are known as conjugate to each other.
Therefore for the hyperbola $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$
Conjugate hyperbola is $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=-1$
Let $\mathrm{e} _{1}$ be the eccentricity of $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ and $\mathrm{e} _{2}$ be
the eccentricity of $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ then $\mathrm{e} _{1}^{2}=1+\frac{\mathrm{b}^{2}}{\mathrm{a}^{2}}=\frac{\mathrm{a}^{2}+\mathrm{b}^{2}}{\mathrm{a}^{2}}$
and $\mathrm{e} _{2}^{2}=1+\frac{\mathrm{a}^{2}}{\mathrm{~b}^{2}}=\frac{\mathrm{b}^{2}+\mathrm{a}^{2}}{\mathrm{~b}^{2}}$
$\therefore \frac{1}{\mathrm{e} _{1}^{2}}+\frac{1}{\mathrm{e} _{2}^{2}}=1$
The foci of a hyperbola and its conjugate hyperbola are concyclic and form the vertices of a square.
Auxiliary circle and eccentric angle
A circle drawn with centre $\mathrm{O}$ and transverse axis as diameter is known as auxiliary circle. Equation of auxiliary circle is $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}$
A is any point on the circle whose coordinates are $(a \cos \theta, a \sin \theta )$, where $\theta$ is known as eccentric angle. Now, In $\triangle \mathrm{OAB}, \mathrm{OA}=\mathrm{a}$
$\cos \theta=\frac{\mathrm{a}}{\mathrm{OB}} \Rightarrow \mathrm{OB}=\mathrm{asec} \theta$
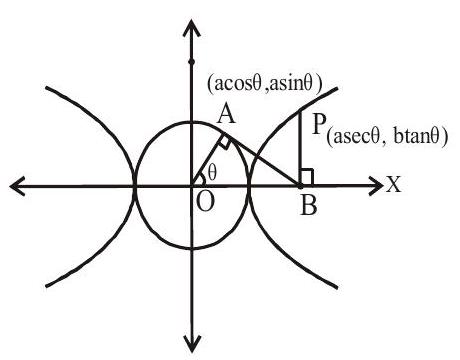
P point lies on hyperbola, so $\frac{\mathrm{a}^{2} \sec ^{2} \theta}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1 \Rightarrow \mathrm{y}= \pm \mathrm{b} \tan \theta$
$ \begin{aligned} & \mathrm{P}(\operatorname{asec} \theta, \operatorname{btan} \theta) \\ & 0 \leq \theta<2 \pi \end{aligned} $
The equations $x=a \sec \theta$ and $y=b \tan \theta$ represents a hyperbola. So, the parametric form of the hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ can be represented as $x=a \sec \theta, y=b \tan \theta$.
For the hyperbola $\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1$, parametric form is $x=h+a \sec \theta ; y=k+b \tan \theta$.
| Hyperbola | Conjugate Hyperbola | |
|---|---|---|
| Equation | $\frac{\mathrm{x}^2}{\mathrm{a}^2}-\frac{\mathrm{y}^2}{\mathrm{~b}^2}=1$ | $-\frac{\mathrm{x}^2}{\mathrm{a}^2}+\frac{\mathrm{y}^2}{\mathrm{~b}^2}=1$ |
| Centre | $(0,0)$ | $(0,0)$ |
| Vertice | $(\mathrm{a}, 0) \&(-\mathrm{a}, 0)$ | $(0, \mathrm{~b}) \&(0,-\mathrm{b})$ |
| Foci | $(\mathrm{ae}, 0) \&(-\mathrm{ae}, 0)$ | $(\mathrm{o}, \mathrm{be}) \&(0,-\mathrm{be})$ |
| Length of transverse axis | $2 \mathrm{a}$ | $2 \mathrm{~b}$ |
| Length of conjugate axis | $2 \mathrm{~b}$ | $2 \mathrm{a}$ |
| Length of latus rectum | $\frac{2 \mathrm{~b}^2}{\mathrm{a}}$ | $\frac{2 \mathrm{a}^2}{\mathrm{~b}}$ |
| Equation of transverse axis | $\mathrm{y}=0$ | $\mathrm{x}=0$ |
| Equation of conjugate axis | $\mathrm{x}=0$ | $\mathrm{y}=0$ |
| Equation of directrices | $\mathrm{x}= \pm \frac{\mathrm{a}}{\mathrm{e}}$ | $\mathrm{y}= \pm \frac{\mathrm{b}}{\mathrm{e}}$ |
| Eccentricity | $\mathrm{e}=\sqrt{1+\frac{\mathrm{b}^2}{\mathrm{a}^2}}$ or $\mathrm{b}^2=\mathrm{a}^2\left(\mathrm{e}^2-1\right)$ | $\mathrm{e}=\sqrt{1+\frac{\mathrm{a}^2}{\mathrm{~b}^2}}$ or $\mathrm{a}^2=\mathrm{b}^2\left(\mathrm{e}^2-1\right)$ |
Examples
1. The point $\left(\frac{a t}{2}+\frac{a}{a t}, \frac{b t}{2}-\frac{b}{2 t}\right)$ lies on the, $[$ for all values of $t(t \neq 0) ]$
(a) circle
(b) parabola
(c) ellipse
(d) hyperbola
Show Answer
Solution:
Let $\mathrm{x}=\frac{\mathrm{at}}{2}+\frac{\mathrm{a}}{2 \mathrm{t}}$ and $\mathrm{y}=\frac{\mathrm{bt}}{2}-\frac{\mathrm{b}}{2 \mathrm{t}}$
$\frac{2 \mathrm{x}}{\mathrm{a}}=\mathrm{t}+\frac{1}{\mathrm{t}}$ and $\frac{2 \mathrm{y}}{\mathrm{b}}=\mathrm{t}-\frac{1}{\mathrm{t}}$
Squaring and subtracting, we get
$ \begin{aligned} & \frac{4 \mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{4 \mathrm{y}^{2}}{\mathrm{~b}^{2}}=4 \\ & \therefore \frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1 \end{aligned} $
Answer: d
2. The position of the point $(5,-4)$ relative to the hyperbola $9 x^{2}-y^{2}=1$ is
(a) on the hyperbola
(b) outside the hyperbola
(c) Inside the hyperbola
(d) can not say
Show Answer
Solution:
$ \begin{aligned} & S=9 x^{2}-y^{2}-1 \\ & S _{1}=9(5)^{2}-(-4)^{2}-1=225-16-1=208>0 \end{aligned} $
$\therefore$ point $(5,-4)$ lies inside the hyperbola.
Answer: c.
3. Two circles are given such that they neither intersect nor touch. The locus of centre of variable circle which touches both the circles externally is
(a) a circle
(b) a parabola
(c) an ellipse
(d) a hyperbola
Show Answer
Solution:
Let radii of the fixed circles be $r _{1}$ and $r _{2}$ and radius of variable circle be $\mathrm{r}$
Let variable circles with centre $\mathrm{C}$ touches two fixed circles with centre $\mathrm{C} _{1}$ and $\mathrm{C} _{2}$.
Then $\mathrm{CC} _{1}=\mathrm{r}+\mathrm{r} _{1}$ and $\mathrm{CC} _{2}=\mathrm{r}+\mathrm{r} _{2} \mathrm{CC} _{1}-\mathrm{CC} _{2}=\mathrm{r} _{1}-\mathrm{r} _{2}=$ constant
Locus of $\mathrm{C}$ is hyperbola whose foci are $\mathrm{C} _{1}$ and $\mathrm{C} _{2}$
Answer: d
4: If the latus rectum subtends a right angle at the centre of the hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$, then its eccentricity is
(a) $\frac{\sqrt{5}+1}{2}$
(b) $3$
(c) $\frac{\sqrt{5}}{2}$
(d) $\sqrt{\frac{\sqrt{5}+3}{2}}$
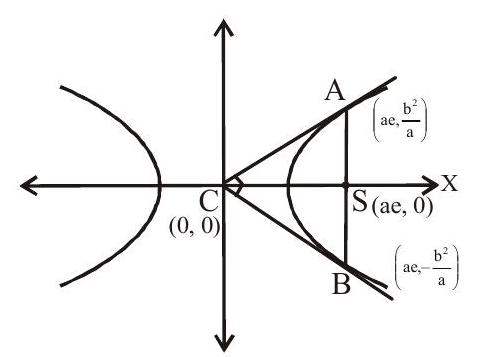
Show Answer
Solution:
$\mathrm{m} _{\mathrm{AC}} \times \mathrm{m} _{\mathrm{BC}}=-1$
$\frac{b^{2}}{\text { a.ae }} \times \frac{-b^{2}}{\text { a.ae }}=-1$
$b^{4}=a^{4} e^{2}$
$\frac{\mathrm{b}^{4}}{\mathrm{a}^{4}}=\mathrm{e}^{2}$
$\left(\mathrm{e}^{2}-1\right)^{2}=\mathrm{e}^{2}$
$\mathrm{e}^{4}-3 \mathrm{e}^{2}+1=0$
$\mathrm{e}^{2}=\frac{3 \pm \sqrt{5}}{2} \Rightarrow \mathrm{e}^{2}=\frac{3+\sqrt{5}}{2} \Rightarrow \mathrm{e}=\sqrt{\frac{3+\sqrt{5}}{2}}$
[if $\mathrm{e}=\sqrt{\frac{3-\sqrt{5}}{2}}<1$ but ecentricity of hyperbola $>1$ so neglecting this value of e]
Answer: d
Practice questions
1. The equation of hyperbola whose foci are $(8,3),(0,3)$ and eccentricity is $\frac{4}{3}$ is
(a). $\frac{(x-4)^{2}}{9}-\frac{(y-3)^{2}}{7}=1$
(b). $\frac{(x-4)^{2}}{7}-\frac{(y-3)^{2}}{9}=1$
(c). $\frac{(x-3)^{2}}{9}-\frac{(y-4)^{2}}{7}=1$
(d). none of these
Show Answer
Answer: (a)2. If $\mathrm{S}$ and $\mathrm{S}^{\prime}$ be the foci, $\mathrm{C}$ the centre and $\mathrm{P}$ be a point on a rectangular hyperbola then $\mathrm{SP} \times \mathrm{S}^{\prime} \mathrm{P}$ is equal to
(a). $2 . \mathrm{SP}$
(b). $(\mathrm{SP})^{2}$
(c). $(\mathrm{CP})^{2}$
(d). $2 . \mathrm{CP}$
Show Answer
Answer: (c)3. If e and $\mathrm{e}^{\prime}$ be the eccentricity of a hyperbola and its conjugate, then
(a). $\frac{1}{\mathrm{e}^{2}}-\frac{1}{\mathrm{e}^{\prime 2}}=1$
(b). $\mathrm{e}^{2}+\mathrm{e}^{\prime 2}=1$
(c). $\mathrm{e}^{2}-\mathrm{e}^{\prime 2}=1$
(d). $ \frac{1}{\mathrm{e}^{2}}+\frac{1}{\mathrm{e}^{\prime 2}}=1$
Show Answer
Answer: (d)4. The foci of a hyperbola coincide with the foci of the ellipse $\frac{x^{2}}{25}+\frac{y^{2}}{9}=1$, The equation of hyperbola if its eccentricity is 2 is
(a). $3 \mathrm{x}^{2}-\mathrm{y}^{2}=12$
(b). $4 x^{2}-y^{2}=12$
(c). $x^{2}-3 y^{2}=12$
(d). $x^{2}-4 y^{2}=12$
Show Answer
Answer: (a)5. The equation $\sqrt{(x-4)^{2}+(y-2)^{2}}+\sqrt{(x+4)^{2}+(y-2)^{2}}=8$ represents
(a). an ellipse
(b). a parabola
(c). a pair of coincident line segment
(d). hyperbola
Show Answer
Answer: (c)6. For hyperbola $\frac{x^{2}}{\cos ^{2} \alpha}-\frac{y^{2}}{\sin ^{2} \alpha}=1$, which of the following remains constant with change in $\alpha$.
(a). abscissae of vertices
(b). abscissae of foci
(c). eccentricity
(d). directrix
Show Answer
Answer: (b)7. Two rods are rotating about two fixed points in opposite directions. If they start from their position of co-incidence and one rotates at the rate double that of the other, then locus of point of intersections of two rods is
(a). a parabola
(b). a circle
(c). an ellipse
(d). a hyperbola
Show Answer
Answer: (d)8. The equations $\frac{x^{2}}{1-r}-\frac{y^{2}}{1+r}=1, r>1$ represents
(a). an ellipse
(b). a circle
(c). a hyperbola
(d). None of these
Show Answer
Answer: (d)9. The equation $2 x^{2}+3 y^{2}-8 x-18 y+35=k$ represents
(a). no locus if $\mathrm{k}>0$
(c). a point if $\mathrm{k}=0$
(b). an ellipse if $\mathrm{k}<0$
(d). a hyperbola if $\mathrm{k}>0$
Show Answer
Answer: (c)10. A hyperbola having the transverse axis of length $2 \sin \theta$ is confocal with the ellipse $3 x^{2}+4 y^{2}=12$. Then its equation is
(a). $x^{2} \operatorname{cosec}^{2} \theta-y^{2} \sec ^{2} \theta=1$
(b). $x^{2} \sec ^{2} \theta-y^{2} \operatorname{cosec}^{2} \theta=1$
(c). $x^{2} \sin ^{2} \theta-y^{2} \cos ^{2} \theta=1$
(d). $x^{2} \cos ^{2} \theta-y^{2} \sin ^{2} \theta=1$
