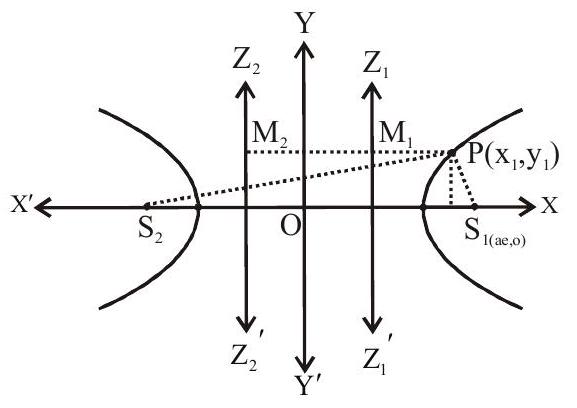
Definition 1 : The locus of (a) point in (a) plane, the difference of whose distance from two fixed points in the plane is constant.

According to definition

$|{\mathrm{PF}}_2-{\mathrm{PF}}_1|=$ constant

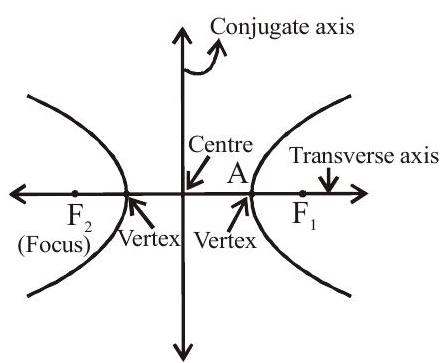
Two fixed points are known as Foci of the hyperbola.

The mid point of the line segment joining the foci is called the centre. The line joining the vertices is known as transverse axis and the line through the centre and perpendicular to transverse axis is known as conjugate axis. The point at which the hyperbola intersect the transverse axis is known as vertices of the hyperbola.

Let distance between two foci be $2(\mathrm{c})$ and distance between two vertices be $2(\mathrm{a})$ and (a) quantity ’ $(\mathrm{b})$ ’ be ${(\mathrm{b})}^2={(\mathrm{c})}^2-{(\mathrm{a})}^2$.

Let (a) point $\mathrm{P}$ on the hyperbola be $(\mathrm{x},\mathrm{y})$, then according to definition of hyperbola $\sqrt{(\mathrm{x}+(\mathrm{c}){)}^2+{\mathrm{y}}^2}-$ $\sqrt{(\mathrm{x}-(\mathrm{c}){)}^2+{\mathrm{y}}^2}=2(\mathrm{a})$ $\sqrt{(x+(c){)}^2+y^2}=2(a)+\sqrt{(x-(c){)}^2+y^2}$

$(x+(c){)}^2+y^2=4(a{)}^2+(x-(c){)}^2+y^2+4(a)\sqrt{(x-(c){)}^2+y^2}[2(a)<2(c)\Rightarrow (a)<(c)]$

$4(c)x-4(a{)}^2=4(a)\sqrt{(x-(c){)}^2+y^2}$

$\frac{(c)x}{(a)}-(a)=\sqrt{(x-(c){)}^2+y^2}$

$\frac{{(\mathrm{c})}^2{\mathrm{x}}^2}{{(\mathrm{a})}^2}+{(\mathrm{a})}^2-2\mathrm{cx}={\mathrm{x}}^2+{(\mathrm{c})}^2-2\mathrm{cx}+{\mathrm{y}}^2$

$\frac{({(\mathrm{c})}^2-{(\mathrm{a})}^2)}{{(\mathrm{a})}^2}{\mathrm{x}}^2-{\mathrm{y}}^2=({(\mathrm{c})}^2-{(\mathrm{a})}^2)$

$\frac{x^2}{(a{)}^2}-\frac{y^2}{(c{)}^2-(a{)}^2}=1\Rightarrow \frac{x^2}{(a{)}^2}-\frac{y^2}{(b{)}^2}=1$

$\frac{x^2}{(a{)}^2}-\frac{y^2}{(b{)}^2}=1$

$\Rightarrow \mathrm{y}=\pm \frac{(\mathrm{b})}{(\mathrm{a})}\sqrt{{\mathrm{x}}^2-{(\mathrm{a})}^2}$

$y$ is real when $x^2\ge (a{)}^2$

$\mathrm{y}$ is real when $\mathrm{x}\ge (\mathrm{a})$ or $\mathrm{x}\le -(\mathrm{a})$

Definition 2: The locus of (a) point which moves in (a) plane such that the ratio of its distance from (a) fixed point to its perpendicular distance from (a) fixed straight line (not passing through given fixed point) is always constant and greater than 1 .

$\frac{\mathrm{PS}}{\mathrm{PM}}=\mathrm{e}>1$

The equation of hyperbola whose focus is the point $(\mathrm{h},\mathrm{k})$ and directrix is $(a)x+(b)y+(c)=0$ and whose eccentricity is $e$, is

$(\mathrm{x}-\mathrm{h}{)}^2+(\mathrm{y}-\mathrm{k}{)}^2={\mathrm{e}}^2\frac{(\mathrm{ax}+\mathrm{by}+(\mathrm{c}){)}^2}{{(\mathrm{a})}^2+{(\mathrm{b})}^2}$

Example: 1 Equation of hyperbola whose focus is $(1,2)$ equations of directrix is $x+y+1=0$ and eccentricity is $\frac{3}{2}$ is

(a) $x^2+y^2-18xy-y-31=0$

(b) $x^2+y^2+18xy+34x+50y-31=0$

(c) $x^2+y^2-18xy-x+y-31=0$

(d) $x^2+y^2+18xy+x+y+31=0$

Eccentricity

$\mathrm{e}=\frac{\text{ Distance between foci }}{\text{ Distance between vertices }}=\frac{2(\mathrm{c})}{2(\mathrm{a})}=\frac{(\mathrm{c})}{(\mathrm{a})}$

${\mathrm{e}}^2=\frac{{(\mathrm{c})}^2}{{(\mathrm{a})}^2}=\frac{{(\mathrm{a})}^2+{(\mathrm{b})}^2}{{(\mathrm{a})}^2}=1+\frac{{(\mathrm{b})}^2}{{(\mathrm{a})}^2}$

${(\mathrm{a})}^2{\mathrm{e}}^2={(\mathrm{a})}^2+{(\mathrm{b})}^2$

$\therefore \frac{{\mathrm{x}}^2}{{(\mathrm{a})}^2}-\frac{{\mathrm{y}}^2}{{(\mathrm{a})}^2({\mathrm{e}}^2-1)}=1$

Some terms related to Hyperbola

Equation of hyperbola $\frac{{\mathrm{x}}^2}{{(\mathrm{a})}^2}-\frac{{\mathrm{y}}^2}{{(\mathrm{b})}^2}=1$

1. Centre

All chords passing through (a) point and bisected at that point is known as centre of hyperbola $\mathrm{C}(0,0)$

2. Eccentricity

$\mathrm{e}=\frac{\text{ Distance between foci }}{\text{ Distance between vertices }}$

$\mathrm{e}=\sqrt{1+\frac{(\text{ conjugate axis }{)}^2}{(\text{ transverse axis }{)}^2}}$ $\mathrm{e}=\frac{\mathrm{PS}}{\mathrm{PM}}$, where $\mathrm{S}$ is focus, $\mathrm{P}$ is any point on the hyperbola, $\mathrm{PM}$ is distance from directrix.

3. Foci

$\mathrm{S}$ and ${\mathrm{S}}^{\prime }$ are foci whose coordinates are $\mathrm{S}(\mathrm{ae},0)$ and ${\mathrm{S}}^{\prime }(-\mathrm{ae},0)$

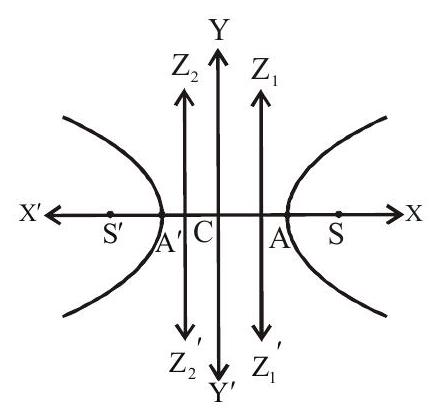
4. Directrices

$Z_1{Z}_1^{\prime }$ and $Z_2{Z}_2^{\prime }$ are the directrices whose equations are $x=\frac{(a)}{e}$ and $x=-\frac{(a)}{e}$

5. Vertices

$A$ and $A^{\prime }$ are the vertices of hyperbola . $A((a),0)$ and $A^{\prime }(-(a),0)$.

6. Axes

The line AA’ is called transverse axis and the line perpendicular to its through the centre of the hyperbola is called conjugate axis. Equations of transverse axis is $y=0$ and equation of conjugate axis is $\mathrm{x}=0$.

Length of transverse axis $=2(\mathrm{a})$

Length of conjugate $\mathrm{axis}=2(\mathrm{b})$

7. Double Ordinate

A chord of hyperbola which is perpendicular to transverse axis is known as double ordinate ${\mathrm{QQ}}^{\prime },\mathrm{Q}(\mathrm{h},\mathrm{k}),{\mathrm{Q}}^{\prime }(\mathrm{h},-\mathrm{k})$.

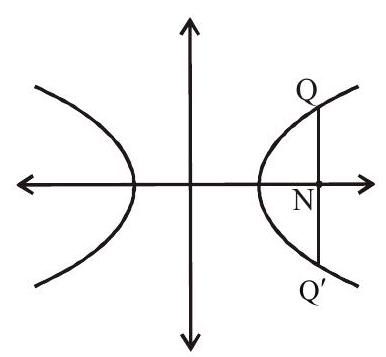
8. Latus rectum

The double ordinates passing through focus is known as latus rectum.

${\mathrm{L}}_1(\mathrm{ae},\frac{{(\mathrm{b})}^2}{(\mathrm{a})}),{\mathrm{L}}_1^{\prime }(\mathrm{ae},-\frac{{(\mathrm{b})}^2}{(\mathrm{a})})$

${\mathrm{L}}_2(-\mathrm{ae},\frac{{(\mathrm{b})}^2}{(\mathrm{a})}),{\mathrm{L}}_2^{\prime }(-\mathrm{ae},-\frac{{(\mathrm{b})}^2}{(\mathrm{a})})$

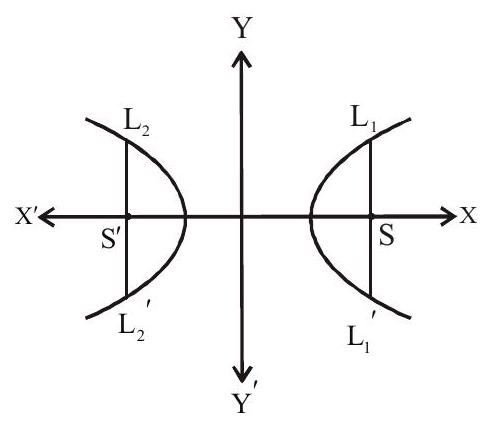
9. Focal Chord

A chord passing through focus is known as focal chord.

10. Focal Distance

${\mathrm{PS}}_1={\mathrm{ePM}}_1=\mathrm{e}({\mathrm{x}}_1-\frac{(\mathrm{a})}{\mathrm{e}})$

$={\mathrm{ex}}_1-(\mathrm{a})$

${\mathrm{PS}}_2=\mathrm{e}({\mathrm{x}}_1+\frac{(\mathrm{a})}{\mathrm{e}})$

$={\mathrm{ex}}_1+(\mathrm{a})$

$\therefore {\mathrm{PS}}_2-{\mathrm{PS}}_1=2(\mathrm{a})$

Rectangular or Equilateral Hyperbola

If $(a)=(b)$, then equation of hyperbola is

${\mathrm{x}}^2-{\mathrm{y}}^2={(\mathrm{a})}^2$ known as rectangular or equilateral hyperbola.

The eccentricity of rectangular hyperbola is

${\mathrm{e}}^2=1+\frac{{(\mathrm{b})}^2}{{(\mathrm{a})}^2}=1+1$

$\mathrm{e}=\sqrt{2}$

Equation of hyperbola if centre is ( $\mathrm{h},\mathrm{k})$ and axes are parallel to coordinate axes is

$\frac{(\mathrm{x}-\mathrm{h}{)}^2}{{(\mathrm{a})}^2}-\frac{(\mathrm{y}-\mathrm{k}{)}^2}{{(\mathrm{b})}^2}=1$

Practice questions

1. The eccentricity of the conic $9x^2-16y^2=144$ is

(a). $\frac{4}{3}$

(b). $\frac{4}{5}$

(c). $\frac{5}{4}$

(d). $\sqrt{17}$

2. The equation of the conic with focus at $(1,-1)$ directrix along $x-y+1=0$ and eccentricity $\sqrt{2}$ is

(a). $xy=1$

(b). $2xy+4x-4y-1=0$

(c). $x^2-y^2=1$

(d). $2xy-4x+4y+1=0$

3. Equation of the hyperbola whose vertices are $(\pm 3,0)$ and foci at $(\pm 5,0)$ is

(a). $9x^2-25y^2=144$

(b). $16x^2-9y^2=144$

(c). $9x^2-16y^2=144$

(d). $25x^2-9y^2=225$

4. The eccentricity of the hyperbola whose latus rectum is half of its transverse axis, is

(a). $\sqrt{\frac{3}{2}}$

(b). $\frac{3}{2}$

(c). $\sqrt{\frac{2}{3}}$

(d). $\frac{2}{3}$

5. The differences of the focal distances of any point on the hyperbola is equal to

(a). eccentricity

(b). latus-rectum

(c). length of conjugate axis

(d). length of transverse axis

6. The distance between the foci of (a) hyperbola is 16 and its eccentricity is $\sqrt{2}$, then equation of the hyperbola is

(a). $x^2-y^2=32$

(b). $x^2-y^2=16$

(c). ${\mathrm{y}}^2-{\mathrm{x}}^2=16$

(d). $y^2-x^2=32$

7. The length of latus rectum of the hyperbola $3x^2-6y^2=-18$ is

(a). $24$

(b). $2\sqrt{3}$

(c). $3\sqrt{2}$

(d). $4\sqrt{3}$

8. The eccentricity of the hyperbola $9x^2-16y^2-18x+32y-151=0$ is

(a). $\frac{5}{3}$

(b). $\frac{5}{4}$

(c). $\frac{5}{2}$

(d). $\sqrt{5}$

9. The foci of (a) hyperbola coincide with the foci of the ellipse $\frac{x^2}{25}+\frac{y^2}{9}=1$. If its eccentricity is 2 then equation of hyperbola is

(a). $\frac{x^2}{12}-\frac{y^2}{4}=1$

(b). $\frac{x^2}{8}-\frac{y^2}{12}=1$

(c). $\frac{x^2}{4}-\frac{y^2}{12}=1$

(d). $x^2-y^2=4$

10. The eccentricity of rectangular hyperbola is

(a). $2$

(b). $1$

(c). $\sqrt{3}$

(d). $\sqrt{2}$