ELLIPSE-3
Topics covered
1. Auxilliary circle
2. Eccentric angle
3. Equation of chord
4. Position of a point with respect to an ellipse.
1. Auxiliary Circle
The circle described on the major axis of an ellipse as diameter is called an auxiliary circle of the ellipse
If
2. Eccentric angle of a point
Let
Draw PM perpendicular to major axis from
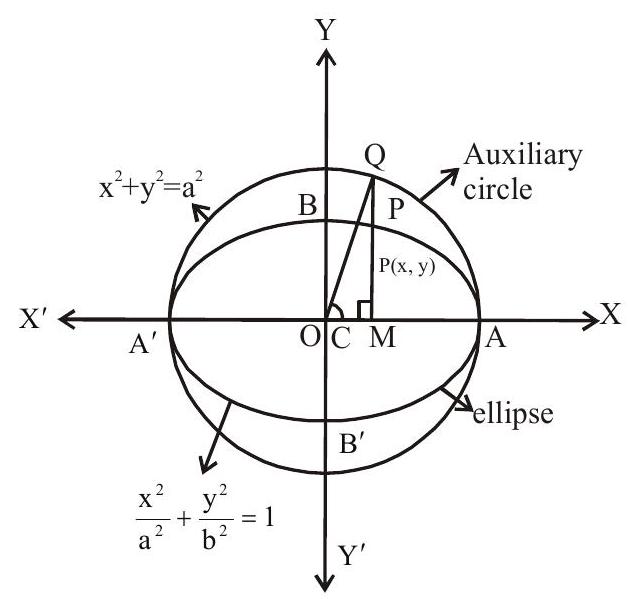
i.e.
3. Equation of the chord
Simplifying the equation we get
4. Position of a point
Let ellipse be
Now P will lie outside, on or inside the ellipse
Examples
1. Find the equation of the curve whose parametric equation are
Show Answer
Solution: We have
Squaring and adding we get
Which is an ellipse.
2. Find the eccentric angle of a point on the ellipse
Show Answer
Solution :
We have
Here centre is origin
3. If
(a)
(b)
(c)
(d)
Show Answer
Solution : Equation of chord joining points having eccentric angles
Since these points are extremities of focal chord so it passes through focus (ae, 0 ) then
Multiply & divide by
4. An ellipse passes through the point
Show Answer
Solution : Let the equation of ellipse be
It passes through
From (1) we get
5. If
Show Answer
Solution : Let
Equation of tangent at this point is
Given that
Comparing (1) and (2) as these two are identical, we get
Practice questions
1. The sum of the squares of the reciprocals of two perpendicular diameter of an ellipse is
(a)
(b)
(c)
(d) None of these
Show Answer
Answer: (a)2. Prove that any point on the ellipse whose foci are
Show Answer
Answer:3. Let
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)4.
(a)
(b)
(c)
(d) None of these
Show Answer
Answer: (a)5. A man running round a race course notes that the sum of the distances of two flag-posts from him is always
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)6. If the line
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)7. If
(a) 1
(b) 2
(c) 3
(d) 4
Show Answer
Answer: (b)8. If equation of the ellipse is
(a) equation of director circle is
(b) director circle will pass through
(c) equation of auxillary circle is
(d) None of these
Show Answer
Answer: (c)9. The foci of ellipse
(a)
(b)
(c)
(d)










