ELLIPSE-1
Topics covered
1. Definition of an Ellipse
2. Standard Equation of an ellipse
3. Basic terminology of ellipse
4. Comparison of standard equation of an ellipse when $a>b$ and $b<a$.
1. Definition of an ellipse
An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant. Fixed points are called focus.
$ \mathrm{PF} _{1}+\mathrm{PF} _{2}=\text { constant } $
2. Standard equation of an ellipse.
$\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ with $\mathrm{a}>\mathrm{b}$.
Where $\mathrm{b}^{2}=\mathrm{a}^{2}\left(1-\mathrm{e}^{2}\right)$
(i) The line containing the two fixed points (foci) is called focal axis (majoraxis) and points of intersection of the curve with focal axis are called the vertices of the ellipse ie. $A(a, 0)$ and $\mathrm{A}^{\prime}(-\mathrm{a}, 0)$.
The distance between $\mathrm{F} _{1}$ and $\mathrm{F} _{2}$ is called the focal length. $\mathrm{F} _{1} \mathrm{~F} _{2}=2 \mathrm{ae}$.
The distance between the vertices is $\mathrm{A}^{\prime}=$ $2 \mathrm{a}$ is called major axis. The distance $\mathrm{BB}^{1}=2 \mathrm{~b}$ is called minor axis
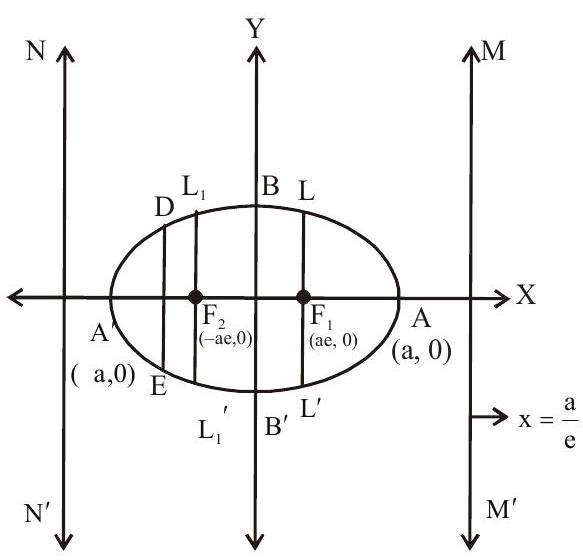
(ii) Point of intersection of the major and minor axis is called the centre of the ellipse. Any chord of the ellipse passing through it gets bisected by it and is called diameter.
(iii) Any chord through focus is called a focal chord and any chord perpendicular to the focal axis is called double ordinate $\mathbf{D E}$.
(iv) A particular double ordinate through focus and perpendicular to focal axis is called its latus rectum ( $\left.L L^{\prime}\right)$. Length of latus rectum $=\frac{2 b^{2}}{a}$
(v) $\mathrm{MM}^{\prime}$ and $\mathrm{NN}^{\prime}$ are two directrices of the ellipse and their equations are $\mathrm{x}=\frac{\mathrm{a}}{\mathrm{e}}$ and $\mathrm{x}$ $=-\frac{\mathrm{a}}{\mathrm{e}}$ respectively
(vi) A chord of the ellipse passing through its focus is called a focal chord.
(vii) An ellipse is the locus of point which moves in a plane such that the ratio of its distance from a fixed point (focus) to the fixed line (directrix) is less than 1. This ratio is called eccentricity and is denoted by e. For an ellipse e $<1$.
(viii) The equation to the ellipse whose focus is (h.k) and directrix is $\ell \mathrm{x}+\mathrm{my}+\mathrm{n}=0$ and whose eccentricity $\mathrm{e}<1$, is $(\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{e}^{2}\left(\frac{\ell \mathrm{x}+\mathrm{my}+\mathrm{n}}{\sqrt{\ell^{2}+\mathrm{m}^{2}}}\right)^{2}$.
(ix) Special form If the centre of the ellipse is at point $(\mathrm{h}, \mathrm{k})$ and the directions of the axis are parallel to the co-ordinate axes, then its equation is $\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$ If we shift the origin at $(\mathrm{h}, \mathrm{k})$ rotating totaling co-ordinate axes then equation of the ellipse with respect to new origin becomes $\frac{X^{2}}{a^{2}}+\frac{Y^{2}}{b^{2}}=1$
Examples
1. The eccentricity of the ellipse $9 x^{2}+5 y^{2}-30 y=0$ is equal to
(a) $1 / 3$
(b) $2 / 3$
(c) $3 / 4$
(d) None of these.
Show Answer
Solution : Here equation of ellipse is
$ \begin{aligned} & 9 x^{2}+5 y^{2}-30 y=0 \\ & 9 x^{2}+5\left(y^{2}-6 y+9-9\right)=0 \\ & 9 x^{2}+5(y-3)^{2}-45=0 \\ & 9 x^{2}+5(y-3)^{2}=45 \\ & \frac{x^{2}}{5}+\frac{(y-3)^{2}}{9}=1 \\ & 9>5 \therefore b>a \\ & a=\sqrt{5} b=3 \end{aligned} $
Hence $\mathrm{e}=\sqrt{1-\frac{\mathrm{a}^{2}}{\mathrm{~b}^{2}}}$
$ \begin{aligned} & =\sqrt{1-\frac{5}{9}} \\ & =\sqrt{\frac{4}{9}} \\ & =2 / 3 \end{aligned} $
2. P is any point on the ellipse $81 x^{2}+144 y^{2}=1944$ whose foci are $S$ and $\mathrm{S}^{\prime}$. Then $\mathrm{SP}+\mathrm{S}^{\prime} \mathrm{P}$ equals.
(a) $4 \sqrt{6}$
(b) $3 \sqrt{6}$
(c) $36$
(d) $324$
Show Answer
Solution : Here equation of ellipse is
$ \begin{aligned} & 81 x^{2}+144 y^{2}=1944 \\ & \frac{x^{2}}{\frac{1944}{81}}+\frac{y^{2}}{\frac{1944}{144}}=1 \end{aligned} $
$ \begin{aligned} & \frac{x^{2}}{24}+\frac{y^{2}}{27}=1 \\ & 24>\frac{27}{2} \\ & \therefore a>b \quad a=2 \sqrt{6} \\ & S P+S^{\prime} P=2 a=4 \sqrt{6} \end{aligned} $
Practice questions
1. The eccentricity of ellipse if length of latus rectum is one-third of major axis
(a) $2 / 3$
(b) $\sqrt{2 / 3}$
(c) $\sqrt{\frac{5}{6}}$
(d) $\left(\frac{3}{4}\right)^{4}$
Show Answer
Answer: (b)2. The curve represented by $x=3(\cos t+\sin t) y=4($ cost-sint $)$ is
(a) Ellipse
(b) Parabola
(c) Hyperbola
(d) Circle
Show Answer
Answer: (a)3. The foci of the ellipse $25(x+1)^{2}+9(y+2)^{2}=225$ are at
(a) $(-1,2) \&(-1,6)$
(c) $(-1,-2) \&(-2,-1)$
(b) $(-2,1) \&(-2,6)$
(d) $(-1,-2) \&(-1,-6)$
Show Answer
Answer: (a)4. The equation $\frac{\mathrm{x}^{2}}{2-\lambda}+\frac{\mathrm{y}^{2}}{\lambda-5}+1=0$ represents an ellipse, if
(a) $\lambda<5$
(b) $\lambda<2$
(c) $2<\lambda<5$
(d) $\lambda<2$ or $\lambda>5$
Show Answer
Answer: (c)5. The sum of the focal distances of any point on the ellipse $9 x^{2}+16 y^{2}=144$ is
(a) 32
(b) 18
(c) 16
(d) 8
Show Answer
Answer: (d)6. The latus rectum of the conic $3 x^{2}+4 y^{2}-6 x+8 y-5=0$
(a) 3
(b) $\frac{\sqrt{3}}{2}$
(c) $\frac{2}{\sqrt{3}}$
(d) None of these
Show Answer
Answer: (a)7. The centre of the ellipse $\frac{(x+y-2)^{2}}{9}+\frac{(x-y)^{2}}{16}=1$ is
(a) $(0,0)$
(b) $(1,1)$
(c) $(1,0)$
(d) $(0,1)$
Show Answer
Answer: (b)8. In an ellipse the distance between its foci is 6 and its minor axis 8 . Then its eccentricity is
(a) $4 / 5$
(b) $\frac{1}{\sqrt{52}}$
(c) $3 / 5$
(d) $1 / 2$
Show Answer
Answer: (c)9. For the ellipse $\mathrm{x}^{2}+4 \mathrm{y}^{2}=9$
(a) The eccentricity is $\frac{1}{2}$
(b) The latus rectum is $\frac{3}{2}$
(c) a focus is $(3 \sqrt{3}, 0)$
(d) a directrix is $x \frac{-2}{\sqrt{3}}$
Show Answer
Answer: (b)10. The difference between the lengths of the major axis and the latus rectum of an ellipse is
(a) $ae$
(b) $2ae$
(c) $\mathrm{ae}^{2}$
(d) $2 \mathrm{ae}^{2}$
