Examples

1. The number of integer values of $m$ for which the $x$-coordinate of the point of intersection of the lines $3 x+4 y=9$ and $y=m x+1$ is also an integer is

(a) 2

(b) 0

(c) 4

(d) 1

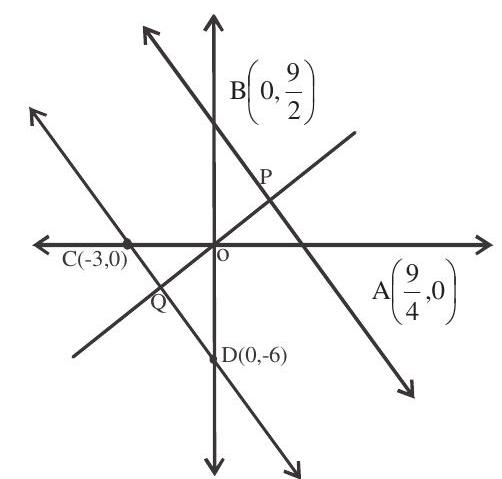
2. A straight line through the origin meets the parallel lines $4 x+2 y=9$ and $2 x+y+6=0$ at points $P$ $\&$ $\mathrm{Q}$ respectively. Then the point $\mathrm{O}$ divides the segment $\mathrm{PQ}$ in the ratio

(a) $1: 2$

(b) $3: 4$

(c) $2: 1$

(d) $4: 3$

Show Answer

Solution: Clearly ${ } _{\Delta} \mathrm{OPA} \sim \Delta \mathrm{OQC}$.

$\Rightarrow \underset{3: 4}{\mathrm{OP}}=\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{9}{3}=\frac{3}{4}$

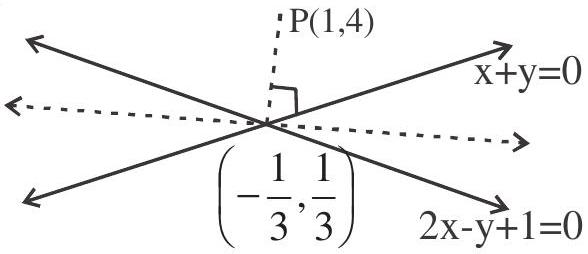
3. A family of lines is given by $(1+2 \lambda) x+(1-\lambda) y+\lambda=0, \lambda$ being the parameter. The line belonging to this family at the maximum distance from the pt $(1,4)$ is

(a) $4 x-y+1=0$

(b) $33 x+12 y+7=0$

(c) $12 x+33 y=7$

(d) None of these.

Show Answer

Solution: $x+y+\lambda(2 x-y+1)=0$

The required line is $y=\frac{1}{3}=\frac{4-\frac{1}{3}}{1+\frac{1}{3}}\left(x+\frac{1}{3}\right) \Rightarrow 12 x+33 y=7$.

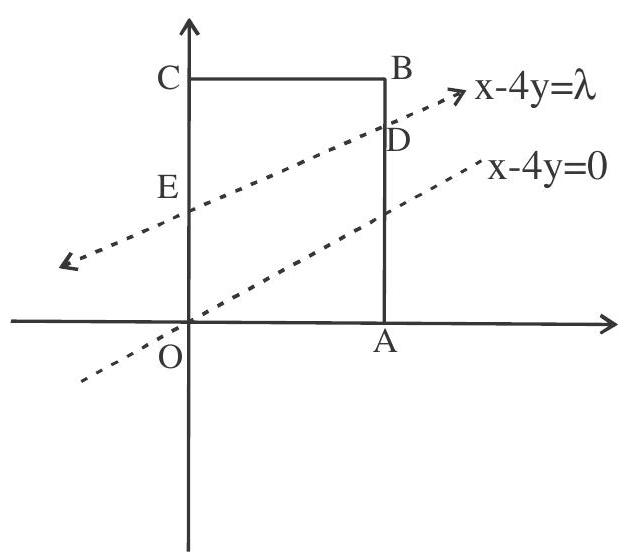
4. The four sides of a quadrilateral are given by the equation $x y(x-2)(y-3)=0$. The equation of the line parallel to $x-4 y=0$ that divides the quadrilateral in two equal areas is

(a) $x-4 y+5=0$

(b) $\mathrm{x}-4 \mathrm{y}-5=0$

(c) $4 y=x+1$

(d) $4 y+1=x$.

Show Answer

Solution: ar.of $\mathrm{OADE}=\frac{1}{2}$ ar $\mathrm{OABC}$

$\frac{1}{2}(\mathrm{OE}+\mathrm{AD}) \times \mathrm{OA}=\frac{1}{2} \times \mathrm{OA} \times \mathrm{AB}$

$\frac{1}{2}\left(-\frac{\lambda}{4}+\frac{2-\lambda}{4}\right) \times 2=\frac{1}{2} \times 2 \times 3$

$\frac{2-2 \lambda}{4}=3$

$\therefore \lambda=-5$

$\therefore$ Equation is $\mathrm{x}-4 \mathrm{y}+5=0$

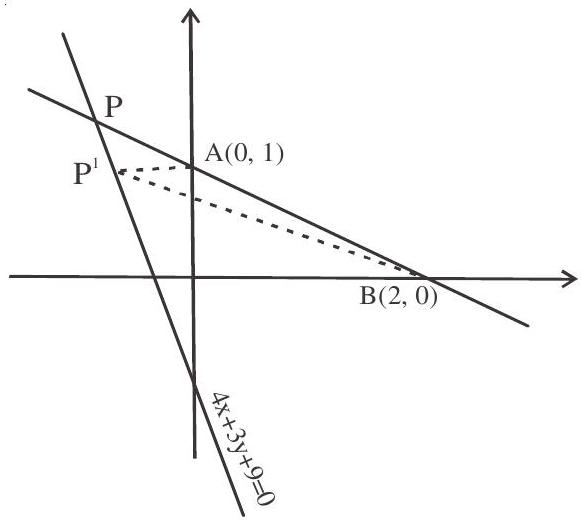
5. Consider the points $\mathrm{A}(0,1)$ and $\mathrm{B}(2,0)$ and $\mathrm{P}$ be a point on the line $4 \mathrm{x}+3 \mathrm{y}+9=0$. Coordinates of $\mathrm{P}$ such that $|\mathrm{PA}-\mathrm{PB}|$ is maximum are

(a) $\left(\frac{-24}{5}, \frac{17}{5}\right)$

(b) $\left(\frac{-18}{5}, \frac{13}{5}\right)$

(c) $\left(\frac{31}{7}, \frac{31}{7}\right)$

(d) $(0,0)$

Show Answer

Solution: $|\mathrm{PA}-\mathrm{PB}| \leq \mathrm{AB}$

Thus IPA-PBI is max. if points A,B,P are collinear. Equation of $A B$ is $y-1=\frac{0-1}{2-1}(x-0) \Rightarrow x+2 y-$ $2=0$

Hence solving $x+2 y-2=0 \& 4 x+3 y+9=0$ we get $\left(\frac{-24}{5}, \frac{17}{5}\right)$

6. A light ray coming along the line $3 x+4 y=5$ gets reflected from the line $a x+b y=1$ and goes along the line $5 x-12 y=10$. Then

(a) $a=\frac{64}{115}, b=\frac{112}{15}$

(b) $\mathrm{a}=\frac{14}{15}, \mathrm{~b}=\frac{-8}{115}$

(c) $\mathrm{a}=\frac{64}{115}, \mathrm{~b}=\frac{-8}{115}$

(d) $\mathrm{a}=\frac{64}{15}, \mathrm{~b}=\frac{14}{15}$

Show Answer

Solution: $a x+b y=1$ will be one of the bisectors of the lines given

$ \begin{aligned} & \frac{3 x+4 y-5}{5}= \pm\left(\frac{5 x-12 y-10}{13}\right) \\ & \Rightarrow 64 x-8 y=115 \quad \text { or } \quad 14 x+112 y=15 \text { On comparing with ax }+b y=1 \text {, we get } \\ & \mathrm{a}=\frac{64}{115}, \mathrm{~b}=\frac{-8}{115} \quad \text { or } \quad \mathrm{a}=\frac{14}{15}, \mathrm{~b}=\frac{112}{15} \end{aligned} $

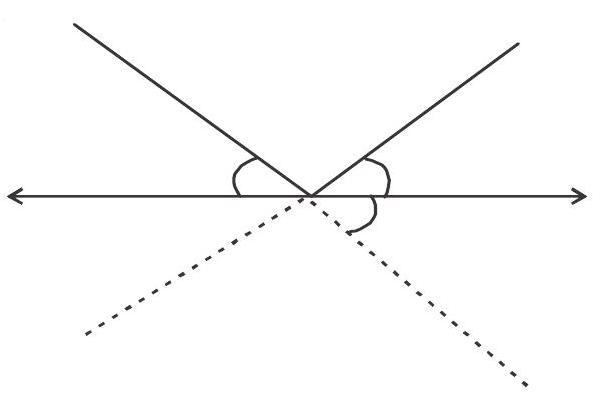
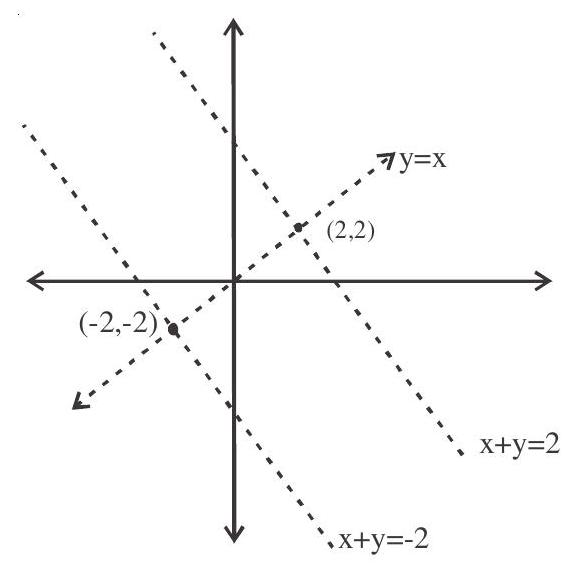
7. If the point $(a, a)$ is placed in between the lines $|x+y|=4$, then $a$ is

(a) $[-2,0]$

(b) $[0,2]$

(c) $(-2,2)$

(d) $[-2,2]$

Show Answer

Solution: $\mathrm{x}+\mathrm{y}=4$

$\mathrm{x}+\mathrm{y}=-4$

$ \& \mathrm{pt}(2,2) \& (-2,-2)$ lies on these lines

Then pt. $(\mathrm{a}, \mathrm{a})$ lies between the lines then $\mathrm{a}>-2$ and $\mathrm{a}<2$ ie. $-2<\mathrm{a}<2$.

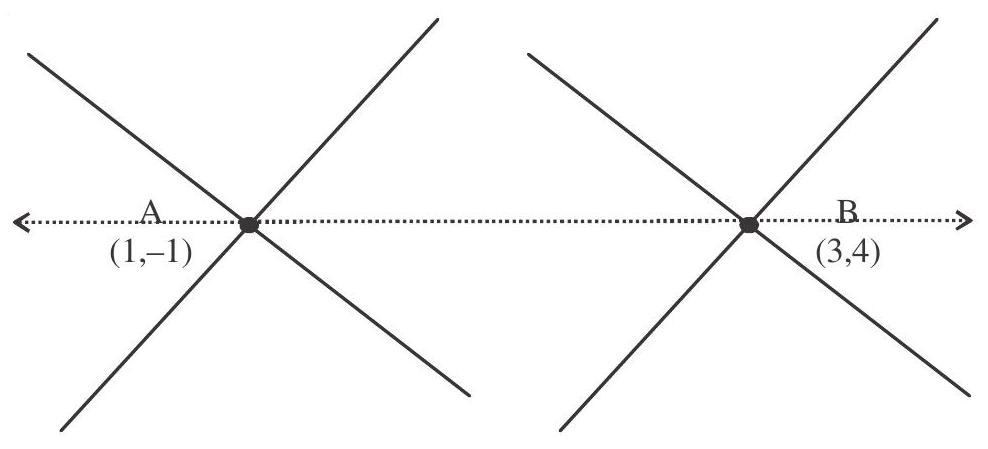
8. Consider the family of lines $5 x+3 y-2+\lambda _{1}(3 x-y-4)=0$ and $x-y+1+\lambda _{2}(2 x-y-2)=0$. The equation of a straight line that belongs to both the families is………….

Show Answer

Solution: Equation of a line belongs to both families passes through $\mathrm{A}$ and $\mathrm{B}$ is

$\begin{aligned} & 5 x+3 y=2 \quad x-y=-1 \\ & \frac{3 x-y=4}{x=1} \quad\quad \frac{2 x-y=2}{x=3} \\ & \quad y=-1 \quad\quad \quad \quad y=4 \\ & \end{aligned}$

$ \begin{aligned} & y+1=\frac{4+1}{3-1}(x-1) \\ & y+1=\frac{5}{2}(x-1) \\ & 5 x-2 y-7=0 \end{aligned} $

9. If $\mathrm{x} _{1}, \mathrm{x} _{2}, \mathrm{x} _{3}$ as well as $\mathrm{y} _{1}, \mathrm{y} _{2}, \mathrm{y} _{3}$ are in G.P. with same common ratio then the points $\mathrm{P}\left(\mathrm{x} _{1}\right.$, $\left.\mathrm{y} _{1}\right), \mathrm{Q}\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right)$ and $\mathrm{R}\left(\mathrm{x} _{3}, \mathrm{y} _{3}\right)$

(a) lie on a straight line

(b) lie on an ellipse

(c) lie on a circle

(d) are vertices of a triangle.

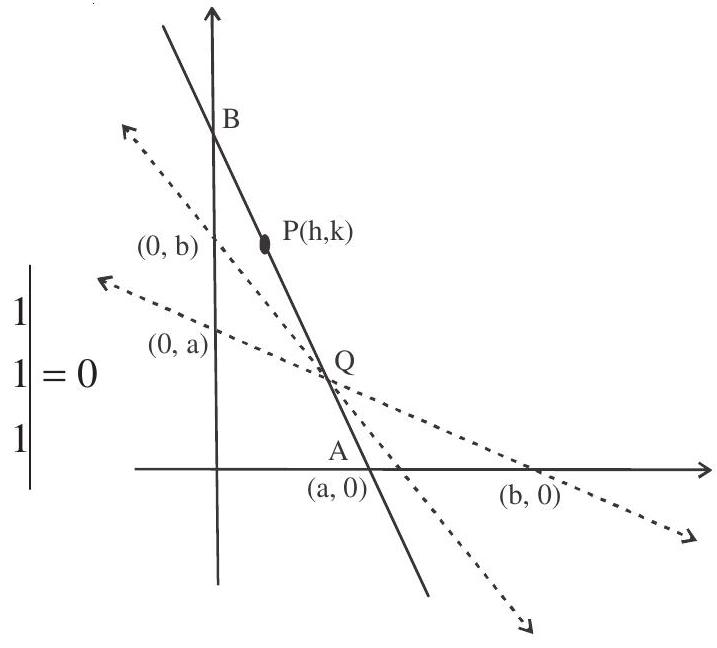
10. A variable straight line is drawn through the point of intersection of the straight lines $\frac{x}{a}+\frac{y}{b}=1$ and $\frac{\mathrm{x}}{\mathrm{b}}+\frac{\mathrm{y}}{\mathrm{a}}=1$ and meets the coordinate axes at $\mathrm{A}$ and $\mathrm{B}$, find the locus of the midpoint of $\mathrm{AB}$.

Show Answer

Solution: Let mid point. of $\mathrm{AB}$ be $(\mathrm{h}, \mathrm{k})$.

Intersection pt. of given lines is $\left(\frac{a b}{a+b}, \frac{a b}{a+b}\right)$

$P$ is mid pt. of $A B \Rightarrow \quad A(2 h, 0) \& B(0,2 k)$.

Now A,B and $Q$ are collinear $\Rightarrow\left|\begin{array}{ccc}2 h & 0 & 1 \\ 0 & 2 k & 1 \\ \frac{a b}{a+b} & \frac{a b}{a+b} & 1\end{array}\right|=0$

$\Rightarrow \quad 4 \mathrm{hk}-\frac{2 \mathrm{hab}}{\mathrm{a}+\mathrm{b}}-\frac{2 \mathrm{kab}}{\mathrm{a}+\mathrm{b}}=0$

$\Rightarrow \quad 2 \mathrm{xy}(\mathrm{a}+\mathrm{b})=\mathrm{ab}(\mathrm{x}+\mathrm{y})$.

Practice questions

1. If the distance of any point $(x, y)$ from origin is defined as $d(x, y)=|x|+|y|$ then the locus of $d(x$, $\mathrm{y})=1$ is a

(a). circle of area $\pi$ sq. units

(b). square of area 1 sq. units

(c). square of area 2 sq. units

(d). none of the above

2. The line $3 x-4 y+7=0$ is rotated through an angle $\frac{\pi}{4}$ in the clockwise direction about the point $(-1,1)$. The equation of the line in its new position is

(a). $7 y+x-6=0$

(b). $7 y-x-6=0$

(c). $7 y+x+6=0$

(d). $7 y-x+6=0$

3. The number of integral values of $m$ for which the $x$-coordinate of the point of intersection of the lines $3 x+4 y=9$ and $y=m x+1$ is also an integer is

(a). 2

(b). 0

(c). 4

(d). 1

4. One of the bisector of the angle between the lines $a(x-1)^{2}+2 h(x-1)(y-1)+b(y-2)^{2}=0$ is $x+2 y-$ $5=0$ The other bisector

(a). $2 \mathrm{x}-\mathrm{y}=0$

(b). $2 x+y=0$

(c). $2 x+y-4=0$

(d). $ x-2 y+3=0$

5. The point $A(2,1)$ is translated parallel to the line $x-y=3$ by a distance 4 units. If the new position $\mathrm{A}$ is in third quadrant, then the coordinates of $\mathrm{A}^{\prime}$ are

(a). $(2+2 \sqrt{2}, 1+2 \sqrt{2})$

(b). $(-2+\sqrt{2},-1-2 \sqrt{2})$

(c). $(2-2 \sqrt{2}, 1-2 \sqrt{2})$

(d). none

6. The orthocenter of the triangle formed by the lines $x+y=1,2 x+3 y=6$ and $4 x-y+4=0$ lies in

(a). I quadrant

(b). II quadrant

(c). III quadrant

(d). IV quadrant

7. The reflection of the point $(4,-13)$ in the line $5 x+y+6=0$ is

(a). $(-1,-14)$

(b). $(3,4)$

(c). $(1,2)$

(d). $(-4,13)$

8. If $\mathrm{p} _{1}, \mathrm{p} _{2}, \mathrm{p} _{3}$ be the length perpendiculars from the points $\left(\mathrm{m}^{2}, 2 \mathrm{~m}\right),\left(\mathrm{mm}^{1}, \mathrm{~m}+\mathrm{m}^{1}\right)$ and $\left(\mathrm{m}^{12}, 2 \mathrm{~m}^{1}\right)$ respectively on the line $x \cos \alpha+y \sin \alpha+\frac{\sin ^{2} \alpha}{\cos \alpha}=0$ then $\mathrm{p} _{1}, \mathrm{p} _{2}, \mathrm{p} _{3}$ are in

(a). $A P$

(b). GP

(c). HP

(d). none of these

9. If $f(+y)=f(x)+f(y), \forall x, y \in R$ and $f(1)=2$, then area enclosed by $3|x|+2|y| \leq 8$ is

(a). $\mathrm{f}(4) \mathrm{sq} . \mathrm{u}$

(b). $\left(\frac{1}{2}\right) \mathrm{f}(16)$ sq. u

(c). $ \frac{1}{3} \mathrm{f}(6) \mathrm{sq} . \mathrm{u}$

(d). $ \frac{1}{3} \mathrm{f}(5)$ sq. u

10. The medians $\mathrm{AD}$ and $\mathrm{BE}$ of the triangle with vertices $\mathrm{A}(\mathrm{o}, \mathrm{b}), \mathrm{B}(\mathrm{o}, \mathrm{o})$ and $\mathrm{C}(\mathrm{a}, \mathrm{o})$ are mutually perpendicular if

(a). $\mathrm{b}=\sqrt{2} \mathrm{a}$

(b). $ a=\sqrt{2} b$

(c). $\mathrm{b}=-\sqrt{2} \mathrm{a}$

(d). $ a=5 \sqrt{2} b$

11. The graph of the function $y=\cos x \cos (x+2)-\cos ^{2}(x+1)$ is

(a). a straight line passing through $\left(0,-\sin ^{2} 1\right)$ with slope 2 .

(b). a straight line passing through $(0,0)$

(c). a parabola with vertex $\left(1,-\sin ^{2} 1\right)$

(d). a straight line passing through the point $\left(\frac{\pi}{2},-\sin ^{2} 1\right)$ parallel to the $x$-axis.

12. If line $2 x+7 y-1=0$ intersect the lines $L _{1}=3 x+4 y+1=0 L _{2}=6 x+8 y-3=0$ in $A$ and $B$ respectively, then equation of a line parallel to $\mathrm{L} _{1}$ and $\mathrm{L} _{2}$ and passes through a point $\mathrm{P}$ such that $\mathrm{AP}: \mathrm{PB}=2: 1$ (internally) is ( $P$ is on the line $2 x+7 y-1=0$ ).

(a). $9 x+12 y+3=0$

(b). $9 x+12 y-3=0$

(c). $9 x+12 y-2=0$

(d). none of these

13. The equation of a line through the point $(1,2)$ whose distance from the point $(3,1)$ has the greatest possible value is

(a). $y=x$

(b). $y=2 x$

(c). $y=-2 x$

(d). $y=-x$

14. If the point $(\cos\theta, \sin\theta)$ does not fall in that angle between the lines $y=|x-1|$ in which the origin lies, the $\theta$ belongs to

(a). $\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)$

(b). $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$

(c). $(0, \pi)$

(d). none of these

15. A line of fixed length $(a+b)$ moves so that its ends are always on two fixed perpendicular lines. The locus of the point which divides this line into portion of lengths $a$ and $b$ is

(a). a circle

(b). an ellipse

(c). a hyper bola

(d). none of these

Numerical grid based problems

Solve the following problems and mark your response against their respective grids. Write your answer in the top row of the grid and darken the concerned numbers in the respective columns.

16. The locus of the moving point $\mathrm{P}$ such that $2 \mathrm{PA}=3 \mathrm{~PB}$ Where $\mathrm{A}$ is $(0,0)$ and $\mathrm{B}$ is $(4,-3)$ is $5 \mathrm{x}^{2}+5 \mathrm{y}^{2}-$ $72 x+\lambda y+\mu=0$ then the value of $\lambda+\mu$ must be.

17. If $(\lambda, 2)$ is an interior point of $\triangle A B C$ formed by $x+y=4,3 x-7 y=8$ and $4 x-y=31$ then $\lambda \varepsilon(a, b)$, the value of $6 a+8 b$ must be.

18. A variable straight line through the point of intersection of the lines $\frac{x}{3}+\frac{y}{4}=1$ and $\frac{x}{4}+\frac{y}{3}=1$ meets the coordinate axes in A and B. If locus of the mid point of $A B$ is $2 x y=k(x+y)$ then the value of $343 \mathrm{k}$ must be

Assertion and Reason (for 19 - 21)

(a). If Assertion is true and reasoing is also true, $\alpha$ and reasoning is a correct explanation for assertion.

(b). If Assertion is True Reasning is also true but reasoing is not correct explanation for Assertion.

(c). Assertion is true reasoning is false Assertion is false is true.

19. Assertion (A) : If centroid and circumcenter by a triangle are known, then its orthocenter and nine point centre can be foun(d).

Reason $(\mathrm{R})$ : Orthocenter, nine point centre, centroid and Circumcenter are collinear.

(a). $A$

(b). $\mathrm{B}$

(c). $\mathrm{C}$

(d). $D$

20. Assertion (A) : The line $2 x+y+6=0$ is perpendicular to the line $x-2 y+5=0$ and second line passes through $(1,3)$

Reason $(\mathrm{R})$ : Product of the slopes of the lines is equal to -1 .

(a). $A$

(b). $B$

(c). $\mathrm{C}$

(d). $D$

21. Assertion (A) : The incenter of the triangle formed by the lines $\mathrm{x} \cos \left(\frac{\pi}{9}\right)+\mathrm{y} \sin \left(\frac{\pi}{9}\right)-\pi=0, \mathrm{x}$ $\cos \left(\frac{\pi}{9}\right)-\mathrm{y} \sin \left(\frac{\pi}{9}\right)+\pi=0$ and $\mathrm{x} \cos \left(\frac{4 \pi}{9}\right)+\mathrm{y} \sin \left(\frac{4 \pi}{9}\right)+\pi=0$ is $(0,0)$

Reason $(R)$ : The point $(0,0)$ is equidistant from the three vertices of the triangle formed by the lines $\mathrm{x} \cos \frac{\pi}{9}+\mathrm{y} \sin \frac{\pi}{9}-\pi=0, \mathrm{x} \cos \frac{\pi}{9}-\mathrm{y} \sin \frac{\pi}{9}+\pi=0, \mathrm{x} \cos \left(\frac{4 \pi}{9}\right)+\mathrm{y} \sin \left(\frac{4 \pi}{9}\right)+\pi=0$

(a). $A$

(b). $B$

(c). $\mathrm{C}$

(d). $D$