Topics Covered

1. Concurrent lines.

2. Equations of angles bisectors.

3. Position of two points relative to a given line.

4. Standard points of triangle.

5. Equations of straight lines through $\left(\mathrm{x} _{1,} \mathrm{y} _{1}\right)$ making angle $\alpha$ with line $\mathrm{y}=\mathrm{mx}+\mathrm{c}$

1. Concurrent lines

The three given lines are concurrent if they meet at one point.

i. Find the point of intersection of any two lines by solving them simultaneously. If this point satisfies the third equation also then the given lines are concurrent.

ii. Let three lines be

$\mathrm{L} _{1}=\mathrm{a} _{1} \mathrm{x}+\mathrm{b} _{1} \mathrm{y}+\mathrm{c} _{1}=0 \mathrm{~L} _{2}=\mathrm{a} _{2} \mathrm{x}+\mathrm{b} _{2} \mathrm{y}+\mathrm{c} _{2}=0$ and

$\mathrm{L} _{3}=\mathrm{a} _{3} \mathrm{x}+\mathrm{b} _{3} \mathrm{y}+\mathrm{c} _{3}=0$ are concurrent if

$ \left|\begin{array}{lll} \mathrm{a} _{1} & \mathrm{~b} _{1} & \mathrm{c} _{1} \\ \mathrm{a} _{2} & \mathrm{~b} _{2} & \mathrm{c} _{2} \\ \mathrm{a} _{3} & \mathrm{~b} _{3} & \mathrm{c} _{3} \end{array}\right|=0 $

iii. The three lines $\mathrm{L} _{1}=0, \mathrm{~L} _{2}=0$ and $\mathrm{L} _{3}=0$ are concurrent if there exist constants , $\mathrm{m}$ and $\mathrm{n}$ not all zero at the same time, such that

$ \mathrm{L} _{1}+\mathrm{mL} _{2}+\mathrm{nL} _{3}=0 $

2. Equations of angle bisectors between two lines

The eqnations of the bisectors of the angles between the lines $a _{1} x+b _{1} y+c _{1}=0$ and $a _{2} x+b _{2} y+c _{2}=0$ are given by $\frac{a _{1} x+b _{1} y+c _{1}}{\sqrt{a _{1}^{2}+b _{1}^{2}}}= \pm \frac{a _{2} x+b _{2} y+c _{2}}{\sqrt{a _{2}^{2}+b _{2}^{2}}}$

i. Any point on a bisector is equidistant from the given lines.

ii. Locus of points which are equidistant from the two intersecting lines is an angle bisector.

iii. Bisectors are perpendicular to each other.

iv. Equation of the bisector of the acute and of obtuse angle between two lines.

Let $\mathrm{a}_2 \mathrm{x}+\mathrm{b} _2 \mathrm{y}+\mathrm{c} _2=0……….(1)$

and $a_2+b_2 y+c_2=0………..(2)$

$\mathrm{c} _1>0, \mathrm{c} _2>0$ then the equation

$\frac{a_1 x+b_1 y+c_1}{\sqrt{a_1^2+b_1^2}}=+\frac{a_2 x+b_2 y+c_2}{\sqrt{a_2^2+b_2^2}}$

is the bisector of the acute or obtuse angle between the lines $1 \& 2$ according as $\mathrm{a} _{1} \mathrm{a} _{2}+\mathrm{b} _{1} \mathrm{~b} _{2}<0$ or $>0$

again $\frac{a _{1} x+b _{1} y+c _{1}}{\sqrt{a _{1}^{2}+b _{1}^{2}}}=-\frac{a _{2} x+b _{2} y+c _{2}}{\sqrt{a _{2}^{2}+b _{2}^{2}}}$ is the bisector of the acute or obtuse angle between the lines $1 \& 2$ according as $\mathrm{a} _{1} \mathrm{a} _{2}+\mathrm{b} _{1} \mathrm{~b} _{2}>0$ or $<0$

3. Position of two points relative to a given line

Let the line be $\mathrm{L}=\mathrm{ax}+\mathrm{by}+\mathrm{c}=0$

$\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ and $\mathrm{A}\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right)$ are two given points.

i. If ax $x _{1}+b y _{1}+c$ and $\mathrm{ax} _{2}+b y _{2}+\mathrm{c}$ both are of the same sign and hence $\frac{a x _{1}+b y _{1}+c}{a x _{2}+b y _{2}+c}>0$ then the points $\mathrm{P}$ and $\mathrm{Q}$ lie on same side of line $\mathrm{ax}+\mathrm{by}+\mathrm{c}=0$

ii. If $\mathrm{ax} _{1}+b \mathrm{by} _{1}+\mathrm{c}$ and $\mathrm{ax} _{2}+\mathrm{by} _{2}+\mathrm{c}$ are of opposite sign and hence $\frac{a x _{1}+b y _{1}+c}{a x _{2}+b y _{2}+c}<0$ then the points $P$ and $Q$ lie on opposite side of the line $a x+b y+c=0$

iii. If origin lie on line then the line is know as origin side.

iv. A point $\left(\mathrm{x} _{1} \mathrm{y} _{1}\right)$ will lie on origin side of the line $\mathrm{ax}+\mathrm{by}+\mathrm{c}=0$ if ax $\mathrm{x} _{1}+\mathrm{by} \mathrm{y} _{1}+\mathrm{c}$ and $\mathrm{c}$ have same sign.

v. A point $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ will lie on non-origin side of the line $\mathrm{ax}+\mathrm{by}+\mathrm{c}=0$ if $\mathrm{ax} _{1}+\mathrm{by} _{1}+\mathrm{c}$ and $\mathrm{c}$ have opposite sign

Family of straight lines

Let $\mathrm{L} _{1}=\mathrm{a} _{1} \mathrm{x}+\mathrm{b} _{1} \mathrm{y}+\mathrm{c} _{1}=0$ and $\mathrm{L} _{2}=\mathrm{a} _{2} \mathrm{x}+\mathrm{b} _{2} \mathrm{y}+\mathrm{c} _{2}=0$

Then the general equation of any straight line passing through the point of intersection of lines $\mathrm{L} _{1}$ and $L _{2}$ is given by $L _{1}+\lambda L _{2}=0$ where $\lambda$ is any real number.

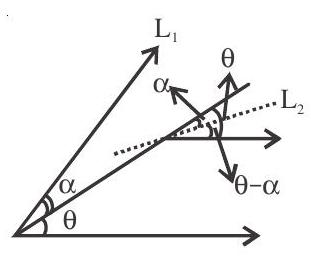
4. Equations of straight lines through $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ making angle $\alpha$ with $\mathrm{y}=\mathrm{mx}+\mathrm{c}$

$\mathrm{y}-\mathrm{y} _{1}=\frac{m+\tan \alpha}{1-m \tan \alpha}\left(x-x _{1}\right)$ and $y-y _{1}=\frac{m-\tan \alpha}{1+m \tan \alpha}\left(x-x _{1}\right)$

5. Standard points of a triangle

1. Centroid or centre of gravity :-

The centroid of a triangle is the point of intersection of its median’s. the centroid divides the median in the ratio 2 : 1 (vertex : base).

Coordinates of G are G $\frac{\mathrm{x} _{1}+\mathrm{x} _{2}+\mathrm{x} _{3}}{3}, \frac{\mathrm{y} _{1}+\mathrm{y} _{2}+\mathrm{y} _{3}}{3}$

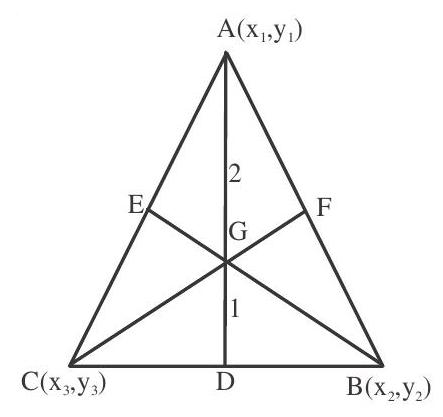
In isosceles triangle median to the equal sides are equal in length and in equilateral triangle all medians are equal in length.

Equations of median can be obtained by using two point form with vertex and the mid point of opposite side.

2. Circumcentre:-

The circumcentre of a triangle is the point of intersection of the perpendicular bisectors of the sides of a triangle.

Coordinates of $\mathrm{O}$ can be obtained from the equation.

$\mathrm{OA}^{2}=\mathrm{OB}^{2}=\mathrm{OC}^{2}$

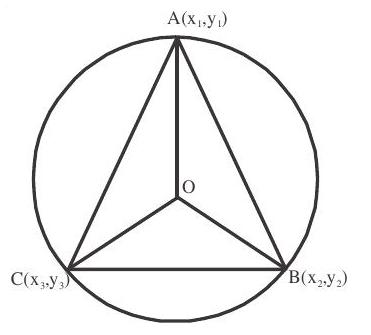
If angles $\mathrm{A}, \mathrm{B}, \mathrm{C}$ and vertices $\mathrm{A}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right), \mathrm{B}\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right)$ and $\mathrm{C}\left(\mathrm{x} _{3}, \mathrm{y} _{3}\right)$ of a $\triangle \mathrm{ABC}$ are given; Then its circumcentre is given by $\frac{x _{1} \sin 2 A+x _{2} \sin 2 B+x _{3} \sin 2 C}{\sin 2 A+\sin 2 B+\sin 2 C}, \frac{y _{1} \sin 2 A+y _{2} \sin 2 B+y _{3} \sin 2 C}{\sin 2 A+\sin 2 B+\sin 2 C}$

The circumcentre of a right-angled triangle is the mid-point of its hypotenuse. Therefore the mid-point of hypotenuse is equidstant from its vertices

$\mathrm{AM}=\mathrm{BM}=\mathrm{CM}$

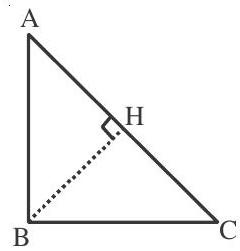
The circumcentre of the triangle formed by $(0,0),\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ and $\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right)$ is

$ \frac{\mathrm{y} _{2}\left(\mathrm{x} _{1}^{2}+\mathrm{y} _{1}^{2}\right)-\mathrm{y} _{1}\left(\mathrm{x} _{2}^{2}+\mathrm{y} _{2}^{2}\right)}{2\left(\mathrm{x} _{1} \mathrm{y} _{2}-\mathrm{x} _{2} \mathrm{y} _{1}\right)}, \frac{\mathrm{x} _{2}\left(\mathrm{x} _{1}^{2}+\mathrm{y} _{1}^{2}\right)-\mathrm{x} _{1}\left(\mathrm{x} _{2}^{2}+\mathrm{y} _{2}^{2}\right)}{2\left(\mathrm{x} _{2} \mathrm{y} _{1}-\mathrm{x} _{1} \mathrm{y} _{2}\right)} $

3. Incentre of a triangle:-

The point of intersection of the internal bisecters of the angles of a triangle is called the incentre of the triangle.

The coordinates of the incentre of a triangle with vertices $\left(\mathrm{x} _{1,} \mathrm{y} _{1}\right),\left(\mathrm{x} _{2,} \mathrm{y} _{2}\right)$ and $\left(\mathrm{x} _{3}, \mathrm{y} _{3}\right)$ are

$ \frac{a x _{1}+b x _{2}+c x _{3}}{a+b+c}, \frac{a y _{1}+b y _{2}+c y _{3}}{a+b+c} $

Where $a, b, c$ are lengths of sides of triangle

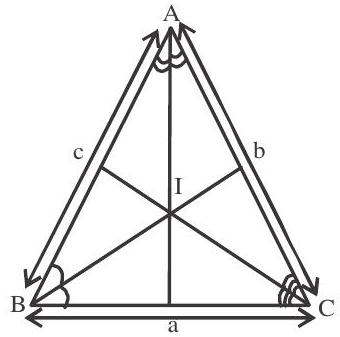
The incentre of the triangle formed by $(0,0),(a, 0),(0, b)$ is $\frac{a b}{a+b+\sqrt{a^{2}+b^{2}}}, \frac{a b}{a+b+\sqrt{a^{2}+b^{2}}}$

4. Orthotcentre:-

The orthocentre of a triangle is a point intersection of altitudes.

i. Take the equations of any two sides of a triangle. find the eqnations the lines perpendicular to those lines and passing through the opposite vertices. solve these two equations we get orthocentre of the triangle.

ii. If angles $\mathrm{A}, \mathrm{B}, \mathrm{C}$ and vertices $\mathrm{A}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right) \mathrm{B}\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right)$ and $\mathrm{C}\left(\mathrm{x} _{3}, \mathrm{y} _{3}\right)$ of a $\triangle \mathrm{ABC}$ are given then orthocentre of $\triangle \mathrm{ABC}$ is given by

$ \frac{x _{1} \tan A+x _{2} \tan B+x _{3} \tan C}{\tan A+\tan B+\tan C}, \frac{y _{1} \tan A+y _{2} \tan B+y _{3} \tan C}{\tan A+\tan B+\tan C} $

iii. If any two lines out of three lines $\mathrm{AB}, \mathrm{BC}, \mathrm{CA}$, are perpendicular, then orthocentre is the point of intersection of two perpendicular lines.

iv. The orthocentre of the triangle with verties $(0,0),\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ and $\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right)$ is

$ \left(\mathrm{y} _{1}-\mathrm{y} _{2}\right) \frac{\mathrm{x} _{1} \mathrm{x} _{2}-\mathrm{y} _{1} \mathrm{y} _{2}}{\mathrm{x} _{2} \mathrm{y} _{1}-\mathrm{x} _{1} \mathrm{y} _{2}},\left(\mathrm{x} _{1}-\mathrm{x} _{2}\right) \frac{\mathrm{x} _{1} \mathrm{x} _{2}+\mathrm{y} _{1} \mathrm{y} _{2}}{\mathrm{x} _{1} \mathrm{y} _{2}-\mathrm{x} _{2} \mathrm{y} _{1}} $

v. The orthocentre $(\mathrm{O})$, centroid $(\mathrm{G})$ and circumcentre $(\mathrm{C})$ of any triangle lie in a straight line and $\mathrm{G}$ divides the join of $\mathrm{O}$ and $\mathrm{C}$ in the Ratio $2: 1$

vi. In an equilateral triangle,orthocentre, centroid, circumcentre and incentre coinside.

5. Coordinates of nine point circle :-

If a circle passes through the feet of perpendicular (D,E,F) mid points of sides $\mathrm{BC}, \mathrm{CA}, \mathrm{AB}$ sespectivcly $(\mathrm{H}, \mathrm{I}, \mathrm{J})$ and mid points of the line joining the orthocentre $\mathrm{O}$ to the angular points A,B,C (K,L,M) thus the nine points D,E,F H,I,J, K,L,M all lie on a circle, This circle is known as nine point circle and its centre is called nine point centre.

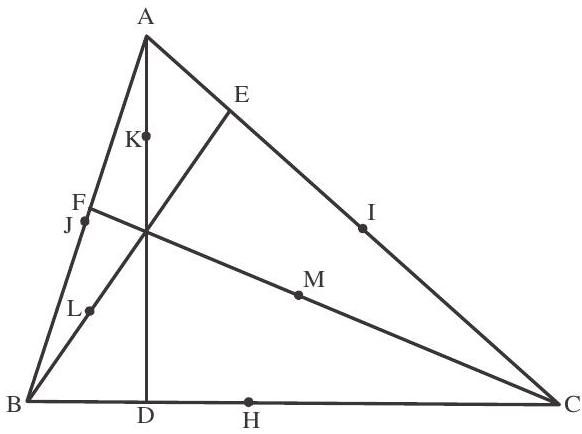
1. The orthocentre $(\mathrm{O})$, nine point centre $(\mathrm{N})$ centroid $(\mathrm{G})$ and circumcentre $(\mathrm{C})$ all lie in the same line i.e. ONGC (oil natural gas corporation)

2. The nine point centre bisects the join of orthocentre $(\mathrm{O})$ and circumcentre $(\mathrm{C})$

3. The radius of nine point circle is half the radius of circumcircle.