COORDINATE GEOMETRY - 3 (Straight Line)
Topics Covered
1. Distance of a line from a point
2. Distance between two parallel lines
3. Area of a parallelogram
4. Area of triangle
1. Distance of a line from a point
Length of perpendicular (distance) from the point $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ to the line $\mathrm{ax}+\mathrm{by}+\mathrm{c}=0$ is given by
$\mathrm{p}=\frac{\left|\mathrm{ax} _{1}+\mathrm{by} _{1}+\mathrm{c}\right|}{\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}}$
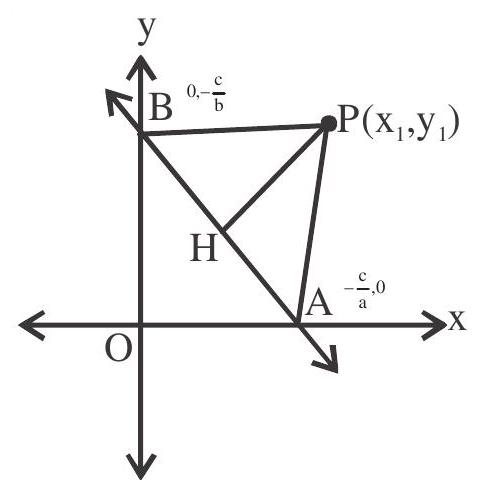
Length of perpendicular from the origin to the line $a x+b y+c=0$ is given by
$\mathrm{p}=\frac{|\mathrm{c}|}{\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}},\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ is $(0,0)$
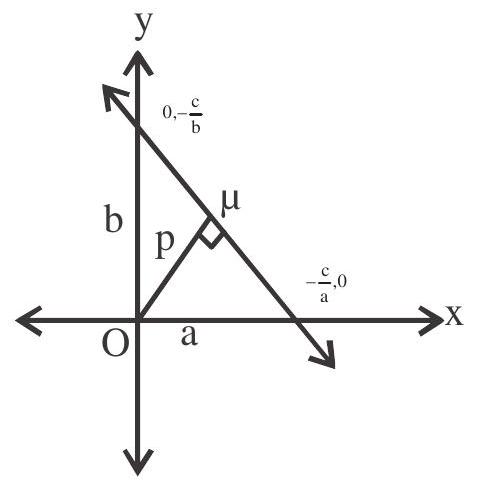
2. Distance between two parallel lines
The distance between two parallel lines $a x+b y+c _{1}=0$ and $a x+b y+c _{2}=0$ is given by
$\mathrm{p}=\frac{\left|\mathrm{c}_1-\mathrm{c}_2\right|}{\sqrt{\mathrm{a}^2+\mathrm{b}^2}}$
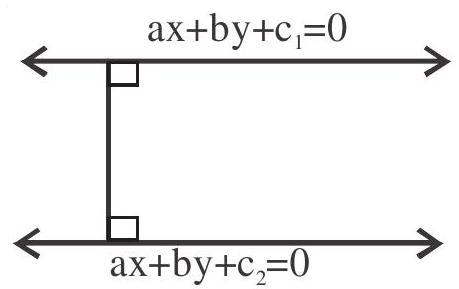
Note that coefficient of $x$ and $y$ of both equation must be same.
3. Area of a parallelogram
Area of a parallelogram $\mathrm{ABCD}=2$ area of $\triangle \mathrm{ABD}$
$ \begin{aligned} & \mathrm{A}=\mathrm{z}\left(\frac{1}{2} \times \mathrm{AB} \times \mathrm{AD} \times \sin \theta\right) \\ & \mathrm{A}=\mathrm{AB} \times \mathrm{AD} \times \sin \theta \\ & \text { Here }=\frac{\mathrm{PL}}{\mathrm{AD}}=\sin \theta \text { and } \frac{\mathrm{P} 2}{\mathrm{AD}}=\sin \theta \\ & A=\left(\frac{\mathrm{P} _{2}}{\sin \theta}\right)\left(\frac{\mathrm{P} _{1}}{\sin \theta}\right) x \sin \theta \\ & \mathrm{A}=\frac{p _{1} p _{2}}{\sin \theta} \end{aligned} $
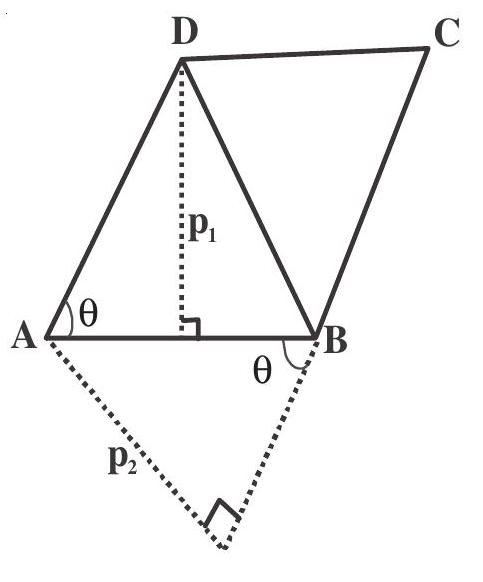
If the sides of a parallelogram be $a _{1} x+b _{1} y+c _{1}=0 ; a _{1} x+b _{1} y+d _{1}=0: a _{2} x+b _{2} y+c _{2}=0, a _{2} x+b _{2} y+d _{2}=$ 0 area of parallelogram $=\left|\frac{\left(c _{1}-d _{1}\right)\left(c _{2}-d _{2}\right)}{\left|\begin{array}{ll}a _{1} & b _{1} \ a _{2} & b _{2}\end{array}\right|}\right|$
Area of Rhombus
In case of a rhombus $\mathrm{p} _{1}=\mathrm{p} _{2}$, area of rhombus $=\frac{p _{1}^{2}}{\sin \theta}$
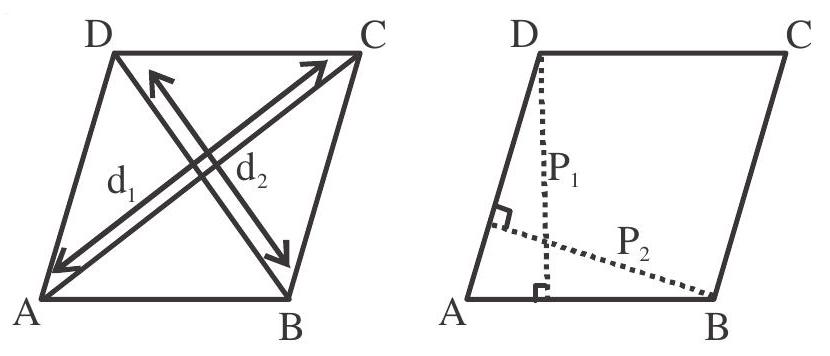
Also area of rhombus $=\frac{1}{2} \mathrm{~d} _{1} \mathrm{~d} _{2}$ where $\mathrm{d} _{1}, \mathrm{~d} _{2}$ are the lengths of two perpendicular diagonals
4. Area of a triangle
Area of a triangle whose vertices are $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right),\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right)$ and $\left(\mathrm{x} _{3}, \mathrm{y} _{3}\right)$ is
$ \frac{1}{2}\left|x _{1}\left(y _{2}-y _{3}\right)+x _{2}\left(y _{3}-y _{1}\right)+x _{3}\left(y _{2}-y _{1}\right)\right| $
$ \begin{aligned} & \text { Or } \frac{1}{2}\left|\begin{array}{ll} \mathrm{x} _{1} & \mathrm{y} _{1} \\ \mathrm{x} _{2} & \mathrm{y} _{2} \\ \mathrm{x} _{3} & \mathrm{y} _{3} \\ \mathrm{x} _{1} & \mathrm{y} _{1} \end{array}\right| \\ & =\frac{1}{2}\left[\left(\mathrm{x} _{1} \mathrm{y} _{2}+\mathrm{x} _{2} \mathrm{y} _{3}+\mathrm{x} _{3} \mathrm{y} _{1}\right)-\left(\mathrm{x} _{2} \mathrm{y} _{1}+\mathrm{x} _{3} \mathrm{y} _{2}+\mathrm{x} _{1} \mathrm{y} _{3}\right)\right] \end{aligned} $
1. If area of a triangle is given then use $\pm$ sign.
2. If three points $\mathrm{A}, \mathrm{B}, \mathrm{C}$ are collinear then area of triangle $\mathrm{ABC}$ is zero.
3. If $a _{1} x+b _{1} y+c _{1}=0 ; a _{2} x+b _{2} y+c _{2}=0$ and $a _{3} x+b _{3} y+c _{3}=0$ are the three sides of a triangle, then the area of the triangle is given by
$ \Delta=\frac{1}{2 \mathrm{C} _{1} \mathrm{C} _{2} \mathrm{C} _{3}}\left|\begin{array}{lll} \mathrm{a} _{1} & \mathrm{~b} _{1} & \mathrm{c} _{1} \\ \mathrm{a} _{2} & \mathrm{~b} _{2} & \mathrm{c} _{2} \\ \mathrm{a} _{3} & \mathrm{~b} _{3} & \mathrm{c} _{3} \end{array}\right|^{2} $
where $\mathrm{C} _{1}=\mathrm{a} _{2} \mathrm{~b} _{3}-\mathrm{a} _{3} \mathrm{~b} _{2}$
$ C _{2}=a _{3} b _{1}-a _{1} b _{3} $
$ C _{3}=a _{1} b _{1}-a _{2} b _{1} $
$\mathrm{C} _{1}, \mathrm{C} _{2}, \mathrm{C} _{3}$ are cofactors of $\mathrm{c} _{1}, \mathrm{c} _{2} \& \mathrm{c} _{3}$
Area of polygon
The area of polygon whose vertices are $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right),\left(\mathrm{x} _{2} \mathrm{y} _{2}\right) \ldots \ldots \ldots \ldots\left(\mathrm{x} _{\mathrm{n} 1} \mathrm{y} _{\mathrm{n}}\right)$
$ =\frac{1}{2}\left|\begin{array}{cc} \mathrm{x} _{1} & \mathrm{y} _{1} \\ \mathrm{x} _{2} & \mathrm{y} _{2} \\ \cdot & \\ \cdot & \\ \cdot & \\ \mathrm{x} _{\mathrm{n}} & \mathrm{y} _{\mathrm{n}} \\ \mathrm{x} _{1} & \mathrm{y} _{1} \end{array}\right|=\frac{1}{2}\left[\left(\mathrm{x} _{1} \mathrm{y} _{2}+\mathrm{x} _{2} \mathrm{y} _{3} \ldots \ldots \ldots \ldots \mathrm{x} _{\mathrm{n}} \mathrm{y} _{1}\right)-\left(\mathrm{y} _{1} \mathrm{x} _{2}+\mathrm{y} _{2} \mathrm{x} _{3} \ldots \ldots \ldots+\mathrm{y} _{\mathrm{n}} \mathrm{x} _{1}\right)\right] $
Examples
1. If the area of the rhombus by the lines $\mathrm{x} \pm \mathrm{my} \pm \mathrm{n}=0$ be 2sq. units then
(a) , $\mathrm{m}, \mathrm{n}$ are in GP
(b) , $\mathrm{n}, \mathrm{m}$ are in GP
(c) $\mathrm{m}=\mathrm{n}$
(d) $\mathrm{L}=\mathrm{m}$.
Show Answer
Solution: (b)
By solving the sides of the rhombus, we get the vertices of rhombus are $(0,-n / m),(-n / \quad, o),(0, n / m)$ and $(\mathrm{n} /, 0)$. Hence the area is $\frac{1}{2} \times \frac{2 \mathrm{n}}{\mathrm{m}} \times \frac{2 \mathrm{n}}{}=2$
$ \therefore \mathrm{n}^{2}=\mathrm{m} . $
Hence , $n, m$ are in GP.
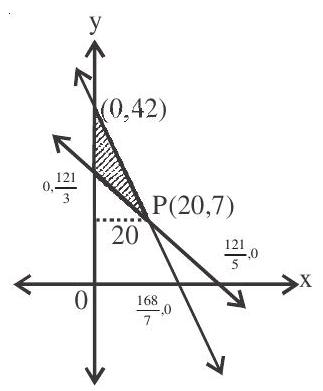
2. The area of the triangular region in the first quadrant bounded on the left by the $y$-axis; bounded above by the line $7 x+4 y=168$ and bounded below by the line $5 x+3 y=121$ is A, then the
value of $\frac{3 \mathrm{~A}}{10}$ is
Show Answer
Solution
Given lines $7 x+4 y=168$ and $5 x+3 y=121$ intersect at $P(20,7)$ by solving these equations Area of shaded region is
$ \begin{aligned} A & =\frac{1}{2}\left(42-40 \frac{1}{3}\right) 20 \\ & =\quad \frac{1}{2} \times \frac{5}{3} \times 20=\frac{50}{3} \text { sq.units } \\ \frac{3 A}{10} & =\frac{3}{10} \times \frac{50}{3}=5 \end{aligned} $
3.
| Column I | Column II |
|---|---|
| (a). Four lines $x+3 y-10=0$ $\mathrm{x}+3 \mathrm{y}-20=0,3 \mathrm{x}-\mathrm{y}+5=0$ and $3 \mathrm{x}-\mathrm{y}-5=0$ form a figure which is | (p). a quadrilateral which is neither parallelogram nor a trapezium |
| (b). The points $\mathrm{A}(1,2), \mathrm{B}(2,-3), \mathrm{C}(-1,-5)$ and $\mathrm{D}(-2,4)$ in order are the vertices of | (q). a parallelogram |
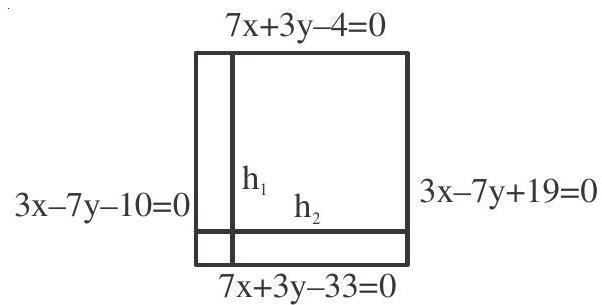
| (c). The lines $7 x+3 y-33=0,3 x-7 y+19=0$, $3 \mathrm{x}-7 \mathrm{y}-10=0$ and $7 \mathrm{x}+3 \mathrm{y}-4=0$ form a figure which is | (r). a rectangle of area 10 sq.units |
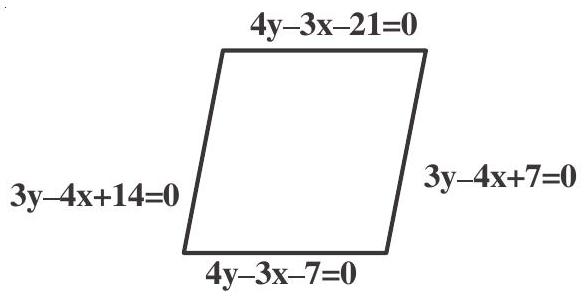
| (d). Four lines $4 y-3 x-7=0,3 y-4 x+7=0$, $4 y-3 x-21=0,3 y-4 x+14=0$ form a figure $s$ a square which is | (s). $a$ square |
Show Answer
Solution:
a $\quad \rightarrow \mathrm{q}, \mathrm{r}, \mathrm{s}$
b $\quad \rightarrow \mathrm{p}$
c $\quad \rightarrow \mathrm{q}, \mathrm{s}$
d $ \rightarrow \mathrm{q}$
a. $\quad \mathrm{h} _{1}=\frac{10}{\sqrt{10}}=\sqrt{10}$
$\mathrm{h} _{2}=\frac{10}{\sqrt{10}}=\sqrt{10}$
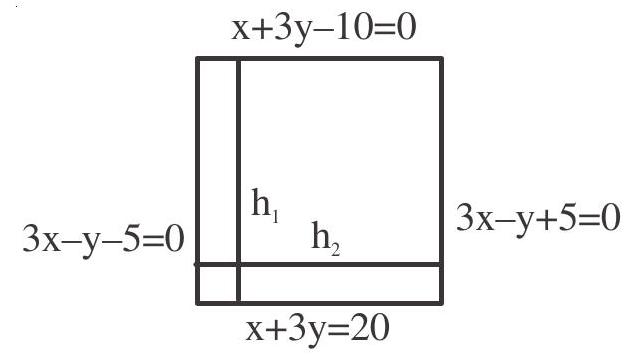
Hence the given lines form a square of side $\sqrt{10}$. Area of a square is $(\sqrt{10})^{2}=10$ sq.units
b. slop of $\mathrm{AB}=\frac{5}{-1}=-5$
slop of $\mathrm{DC}=\frac{9}{-1}=-9$
slop of $\mathrm{AD}=\frac{-2}{3}=\frac{-2}{3}$
slop of $\mathrm{BC}=\frac{2}{3}$
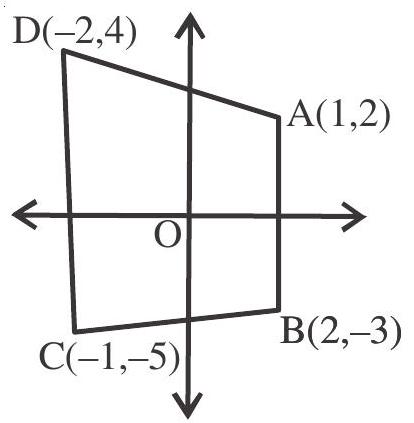
Hence the figure is neither a parallelogram nor a trapezium
c. $\mathrm{h} _{1}=\frac{29}{\sqrt{58}}=\sqrt{\frac{29}{2}}$
$\mathrm{h} _{2}=\frac{29}{\sqrt{58}}=\sqrt{\frac{29}{2}}$
Hence given lines form a square of side $\sqrt{\frac{29}{2}}$ and area $\frac{29}{2}$ sq.units
d. $4 y-3 x-21=0$ and $4 y-3 x-7=0$ are parallel and $3 y-4 x+14=0$ and $3 y-4 x+7=0$ are parallel.
But $4 y-3 x-21=0$ and $3 y-4 x+14=0$ are not perpendicular
Hcnce the given line form a parallelogram.
4. The straight lines $7 \mathrm{x}-2 \mathrm{y}+10=0$ and $7 \mathrm{x}+2 \mathrm{y}-10=0$ form an isosceles triangle with the line $\mathrm{y}=2$.
Area of this triangle is equal to
(a) $\frac{15}{7}$ sq.units
(b) $\frac{10}{7}$ sq.units
(c) $\frac{18}{7}$ sq.units
(d) None
Show Answer
Solution:
$ \mathrm{B}\left(\frac{6}{7}, 2\right) \text { and } \mathrm{C}\left(\frac{-6}{7}, 2\right) $
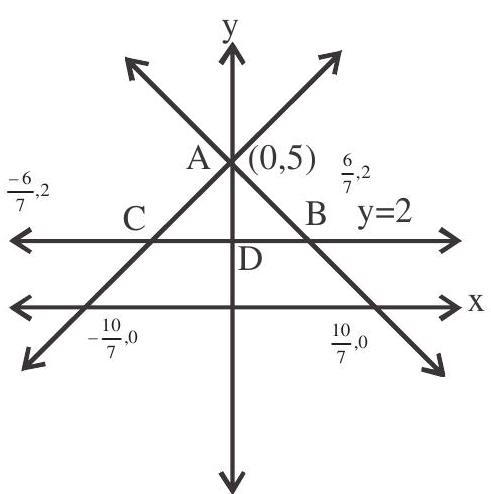 $\mathrm{BC}=\frac{12}{7}$ and $\mathrm{AD}=3$
$\mathrm{BC}=\frac{12}{7}$ and $\mathrm{AD}=3$
area of $\triangle \mathrm{ABC}=\frac{1}{2} \times \frac{12}{7} \times 3$
$ =\frac{18}{7} \text { sq.units. } $
Linked comprehension type
For problems 5 - 7
Let $\mathrm{ABCD}$ be a parallelogram whose equations for the diagonals $\mathrm{AC}$ and $\mathrm{BD}$ are $\mathrm{x}+2 \mathrm{y}=3$ and $2 x+y=3$, respectively. If length of diagonal $A C=4$ units and area of parallelogram $A B C D=8$ sq.units. then
5. The length of other diagonal $\mathrm{BD}$ is
(a) 103
(b) 2
(c) $20 / 3$
(d) None
6. The length of side $\mathrm{AB}$ is equal to
(a) $\frac{2 \sqrt{58}}{3}$
(b) $\frac{4 \sqrt{58}}{9}$
(c) $\frac{3 \sqrt{58}}{9}$
(d) $\frac{5 \sqrt{58}}{9}$
7. The length of $\mathrm{BC}$ is equal to
(a) $\frac{2 \sqrt{10}}{3}$
(B) $\frac{4 \sqrt{10}}{3}$
(C) $\frac{8 \sqrt{10}}{3}$
(d) None
Show Answer
Solution:
5. $\tan \theta=\left|\frac{\frac{-1}{2}+2}{1+1}\right|=\left|\frac{3}{4}\right|$
$\sin \theta=\frac{3}{5}, \quad \cos \theta=\frac{4}{5}$
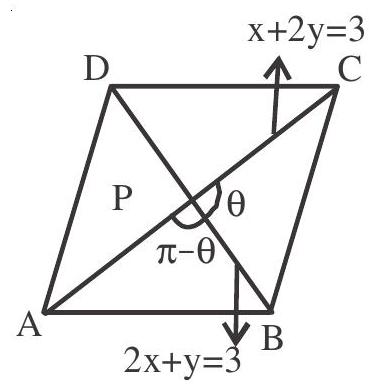
Area of $\Delta \mathrm{CPB}=\frac{1}{2} \mathrm{PC} \times \mathrm{PB} \sin \theta$
$\frac{1}{4} \times 8=\frac{1}{2} \times 2 \times \mathrm{PB} \times \frac{3}{5}$
$\mathrm{PB}=\frac{10}{3}$
$\mathrm{BD}=\frac{20}{3}$ units
6. $\cos (\pi-\theta)=\frac{\mathrm{AP}^{2}+\mathrm{PB}^{2}-\mathrm{AB}^{2}}{2 \mathrm{AP} \times \mathrm{PB}}$
$-\cos \theta=\frac{-4}{5}=\frac{4+\frac{200}{9}-\mathrm{AB}^{2}}{2 \times 2 \times \frac{10}{3}}$
$ \mathrm{AB}=\frac{2 \sqrt{58}}{3} $
7. In ${ } _{\Delta} \mathrm{CPB}, \cos \theta=\frac{P C^{2}+P B^{2}-B C^{2}}{2 \cdot P C \cdot P B}$
$\mathrm{BC}=\frac{2 \sqrt{10}}{3}$
8. Reasoning Type
Statement 1 : The area of the triangle formed by the points $\mathrm{A}(2000,2002), \mathrm{B}(2001,2004) \mathrm{C}(2002$, $2003)$ is same as the area formed by $\mathrm{A}^{1}(0,0), \mathrm{B}^{1}(1,2), \mathrm{C}^{1}(2,1)$
Statement 2 : The area of the triangle is constant with respect to translation of axes.
(a) both the statements are true but statement 2 is the correct explanation of statement 1
(b) both the statement are true but statement 2 is not the correct explanation of statement 1
(c) statement 1 is true and 2 is false
(d) statement 1 is false and 2 is true
Show Answer
Solution :
Area of triangles is unaltered by shifting origin to any point. If origin is shifted to $(2000,2002) \mathrm{A}, \mathrm{B}$, C become $\mathrm{P}(0,0), \mathrm{Q}(1,2), \mathrm{R}(2,1)$ both are true and statement 2 is correct -explanation of statement 1 .
Answer. a










