COORDINATE GEOMETRY - 2 (Straight Line)
Topics Covered
1. Intercept form
2. Normal form
3. Distance form OR Symmetric form OR Parametric form
1. Intercept form
The equation of a straight line which cuts off intercepts $a$ and $b$ on $x$-axis and $y$-axis respectively is given by
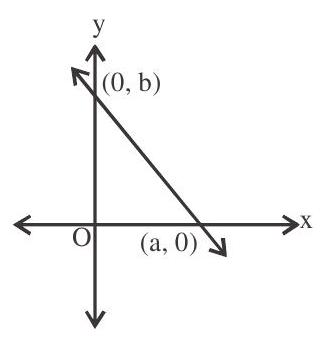
$\frac{\mathrm{x}}{\mathrm{a}}+\frac{\mathrm{y}}{\mathrm{b}}=1$
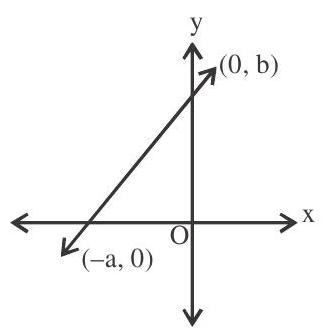
$\frac{-x}{a}+\frac{y}{b}=1$
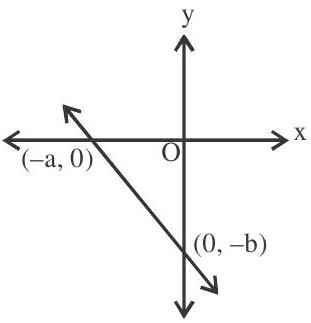
$\frac{\mathrm{x}}{\mathrm{a}}+\frac{\mathrm{y}}{\mathrm{b}}=-1$
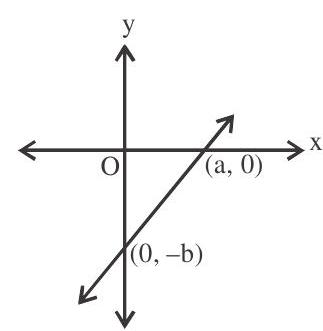
$\frac{x}{a}-\frac{y}{b}=1$
2. Normal form (perpendicular form)
The equation of a straight line upon which the length of the perpendicular from the origin is $p$ and the perpendicular makes an angle $\alpha$ with the positive direction of $\mathrm{x}$-axis is given by $\mathrm{x} \cos \alpha+\mathrm{y} \sin \alpha=\mathrm{p}$
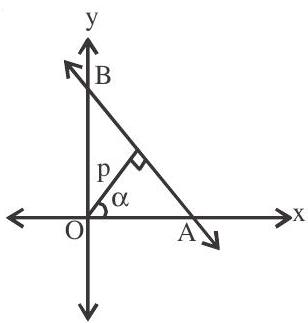
Note Here $\mathrm{p}$ is always taken as positive and $\alpha$ is measured from positive direction of $\mathrm{x}$-axis in anticlockwise direction between 0 and $2 \pi$
3. Distance form or symmetric form or parametric form
The equation of a straight line passing through the point $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ and making an angle $\theta$ with the positive direction of $\mathrm{x}$-axis is given by
$\frac{\mathrm{x}-\mathrm{x} _{1}}{\cos \theta}=\frac{\mathrm{y}-\mathrm{y} _{1}}{\sin \theta}=\mathrm{r}$
Where $r$ is the distance of the point $(x, y)$ from the point $\left(x _{1}, y _{1}\right)$
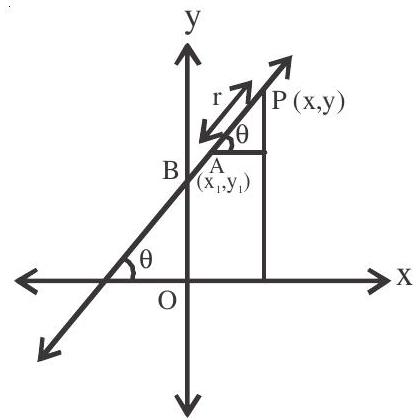
Parametric form
From the above equation we get
$x-x _{1}=r \cos \theta, \quad y-y _{1}=r \sin \theta$
$x=x _{1}+\operatorname{rcos} \theta \quad y=y _{1}+\sin \theta$
The coordinates $(\mathrm{x}, \mathrm{y})$ of any point on the line at a distance $\mathrm{r}$ from the point $\mathrm{A}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ can be taken as $\left(\mathrm{x} _{1}+\mathrm{r} \cos \theta, \mathrm{y} _{1}+\mathrm{r} \sin \theta\right)$
Where the line is inclined at an angle $\theta$ with positive direction of $\mathrm{x}$-axis.
1. If $\mathrm{P}$ is on the right side of $\mathrm{A}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ then $\mathrm{r}$ is positive and if $\mathrm{p}$ is on the left side of $\mathrm{A}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ then $r$ is negative.
2. At a given distance $r$ from the point $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ on the line $\frac{\mathrm{x}-\mathrm{x} _{1}}{\cos \theta}=\frac{\mathrm{y}-\mathrm{y} _{1}}{\sin \theta}$, there are two points viz; $\left(\mathrm{x} _{1}+\mathrm{r} \cos \theta, \mathrm{y} _{1}+\mathrm{r} \sin \theta\right)$ and $\left(\mathrm{x} _{1}-\mathrm{r} \cos \theta, \mathrm{y} _{1}-\mathrm{r} \sin \theta\right)$
Examples
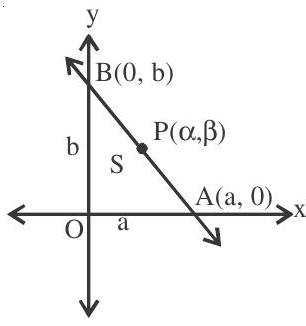
1. Through the point $\mathrm{P}\left(\alpha _{1} \beta\right)$ where $\alpha \beta>0$ the straight line $\frac{\mathrm{x}}{\mathrm{a}}+\frac{\mathrm{y}}{\mathrm{b}}=1$ is drawn so as to form with coordinate axes a triangle of area $\mathrm{S}$. If $\mathrm{ab}>0$ then the least value of $\mathrm{S}$ is
(a) $\alpha \beta$
(b) $2 \alpha \beta$
(c) $4 \alpha \beta$
(d) None.
Show Answer
Solution:
Given equation of line is $\frac{\mathrm{x}}{\mathrm{a}}+\frac{\mathrm{y}}{\mathrm{b}}=1………..(1)$
area of $\triangle \mathrm{OAB}=\mathrm{S}$
$ \left|\frac{1}{2} a b\right|=S $
Or $\mathrm{ab}=2 \mathrm{~S}$
$a b>0$
Equation (1) passes through the point $\mathrm{P}(\alpha, \beta)$
$ \frac{\alpha}{a}+\frac{\beta}{b}=1 \quad \text { or } \quad \frac{\alpha}{a}+\frac{a \beta}{a b}=1 $
$ \begin{aligned} & \frac{\alpha}{a}+\frac{a \beta}{2 S}=1 \\ & a^{2} \beta-2 a S+2 S \alpha=0 \\ & \quad \quad \text { is real } \\ & \therefore D \geq 0 \\ & 4 S^{2}-8 S \alpha \beta \geq 0 \\ & S^{2}-2 S \alpha \beta \geq 0 \\ & S \geq 2 \alpha \beta \end{aligned} $
$\therefore$ least value of $\mathrm{S}$ is $2 \alpha \beta$.
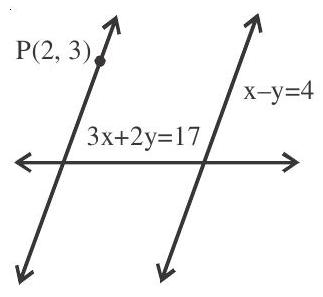
2. The distance of the point $(2,3)$ from the line $3 x+2 y=17$ measured parallel to the line $x-y=4$ is
(a) $4 \sqrt{2}$
(b) $5 \sqrt{2}$
(c) $\sqrt{2}$
(d) None.
Show Answer
Solution:
Any point of the line parallel to $x-y=4$ and passes through $P(2,3)$ at a distance $r$, are $(2+r \cos \theta, 3+r \sin \theta)$ where $\tan \theta=1=$ slope of line $x-y=4$ therefore $\theta=45^{\circ}=\frac{\pi}{4}$
This point lies on the line $3 \mathrm{x}+2 \mathrm{y}=17$
$\therefore 6+3 r \cos 45^{\circ}+6+2 r \sin 45^{\circ}=17$
$6+\frac{3 \mathrm{r}}{\sqrt{2}}+6+\frac{2 \mathrm{r}}{\sqrt{2}}=17$
$\frac{5 \mathrm{r}}{\sqrt{2}}=5$
$\frac{\mathrm{r}}{\sqrt{2}}=1$
$\mathrm{r}=\sqrt{2}$
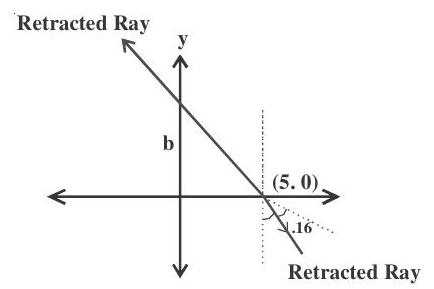
3. A ray of light travelling along the line $x+\sqrt{3} y=5$ is incident on the $x$-axis and after refraction it enters the other side of the $\mathrm{x}$-axis by turning $\pi / 6$ away from the $\mathrm{x}$-axis. The equation of the line along which the refracted ray travels is
(a) $x+\sqrt{3} y-5 \sqrt{3}=0$
(b) $x-\sqrt{3} y-5 \sqrt{3}=0$
(c) $\sqrt{3} x+y-5 \sqrt{3}=0$
(d) $\sqrt{3} x-y-5 \sqrt{3}=0$
Show Answer
Solution : The refracted ray passes through the point $(5,0)$ and makes an angle $120^{\circ}$ with positive direction of $\mathrm{x}$-axis
$\therefore$ The equation of the refracted ray is
$\mathrm{y}-0=\tan 120^{\circ}(\mathrm{x}-5)$
$\mathrm{y}=-\sqrt{3}(\mathrm{x}-5)$
$\sqrt{3} \mathrm{x}+\mathrm{y}-5 \sqrt{3}=0$
4. Column Matching (This Q. is not relevant as option the righthand coloumn are unique) easily identifide.
| Column I | Column II |
|---|---|
| 1. It a, b, c are in H.P, then the straight line $\frac{\mathrm{x}}{\mathrm{a}}+\frac{\mathrm{y}}{\mathrm{b}}+\frac{1}{\mathrm{c}}=0 \text { always passes through } \mathrm{a}\text { fixed point }$ | (a) $\frac{\pi}{2}$ |
| 2. The larger of the two angles made with the axis of a straight line drawn through $(1,2)$ so that it intersects $\mathrm{x}+\mathrm{y}=4$ at a point distant $\frac{\sqrt{6}}{3}$ from $(1,2)$ is | (b) $(1, -2)$ |
| 3. The diagonals of the parallelogram whose sides are $1 \mathrm{x}+\mathrm{my}+\mathrm{n}=0$,$1 \mathrm{x}+\mathrm{my}+\mathrm{n}^{1}=0, \mathrm{mx}+\mathrm{ly}+\mathrm{n}=0$ | (c) Rhombus |
| 4. The diagonals of a parallelogram $\mathrm{PQRS}$ are along the lines $\mathrm{x}+3 \mathrm{y}=4$ and $6 x-2 y=7$. Then PQRS must be a | (d) $\frac{5 \pi}{12}$ |
Show Answer
Solution :
1. a, b, c are in H.P so $\frac{1}{\mathrm{a}}, \frac{1}{\mathrm{~b}}, \frac{1}{\mathrm{c}}$ are in A.P
$\therefore \frac{2}{\mathrm{~b}}=\frac{1}{\mathrm{a}}+\frac{1}{\mathrm{c}}$
or $\frac{1}{\mathrm{a}}-\frac{2}{\mathrm{~b}}+\frac{1}{\mathrm{c}}=0=\frac{\mathrm{x}}{\mathrm{a}}+\frac{\mathrm{y}}{\mathrm{b}}+\frac{1}{\mathrm{c}}$
on comparing $\mathrm{x}=1, \mathrm{y}=-2 \quad$ so coordinate $\quad(1,-2)$
2. $\mathrm{AP}=\mathrm{r}=\frac{\sqrt{6}}{3}$
Equation of $\mathrm{AP} \Rightarrow \frac{\mathrm{x}-1}{\cos \theta}=\frac{\mathrm{y}-2}{\sin \theta}=\mathrm{r}$
$\therefore \mathrm{P}(1+\mathrm{r} \cos \theta, 2+\mathrm{r} \sin \theta)$
$P$ will satisfy $x+y=4$
$\therefore 1+\frac{\sqrt{6}}{3} \cos \theta+2+\frac{\sqrt{6}}{3} \sin \theta=4$
$\cos \left(\theta-\frac{\pi}{4}\right)=\frac{\sqrt{3}}{2}=\cos 30^{\circ}$
$\therefore \theta=75^{\circ}$ or $15^{\circ}$ ie, $\frac{5 \pi}{12}$ or $\frac{\pi}{12}$

3. Since the distance between parallel lines $L x+m y+n=0$ and $L x+m y+n^{\prime}=0$ is same as the distance between the parallel lines $m x+l y+n=0$ and $m x+l y+n^{1}=0$. ie, $\left|\frac{n-n^{\prime}}{\sqrt{L^{2}+m^{2}}}\right|$ there fore the parallelogram is a rhombus. Since the diagonals of a rhombus are at right angles, therefore the required angle is $\frac{\pi}{2}$.
4. Slope of line $x+3 y=4$ is $\frac{-1}{3}$
slope of line $6 x-2 y=7$ is $\frac{6}{2}=3$
product of slopes $=\frac{-1}{3} \times 3=-1$
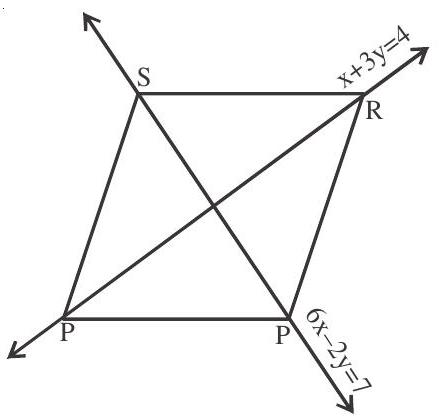
$\therefore$ diagonals are perpendicular to each other
Answers

Practice questions
1. Orthocenter of triangle with vertices $(0,0),(3,4)$ and $(4,0)$ is
(a) $\left(3, \frac{5}{4}\right)$
(b) $(3,12)$
(c) $\left(3, \frac{3}{4}\right)$
(d) $(3,9)$
Show Answer
Answer: (c)2. Area of the triangle formed by the line $x+y=3$ and angle bisectors of the pairs of straight lines $\mathrm{x}^{2}-\mathrm{y}^{2}+2 \mathrm{y}=1$ is
(a) 2 sq.units
(b) 4 sq.units
(c) 6sq.units
(d) 8 sq.units
Show Answer
Answer: (a)3. Let $\mathrm{O}(0,0), \mathrm{P}(3,4), \mathrm{Q}(6,0)$ be the vertices of the triangle $\mathrm{OPQ}$. The point $\mathrm{R}$ inside the $\Delta \mathrm{OPQ}$ is such that the triangle OPR, PQR, OQR are of equal area. The coordinates of $\mathrm{R}$ are
(a) $\left(\frac{4}{3}, 3\right)$
(b) $\quad\left(3, \frac{2}{3}\right)$
(c) $\left(3, \frac{4}{3}\right)$
(d) $\left(\frac{4}{3}, \frac{2}{3}\right)$
Show Answer
Answer: (c)4. Consider three points $\mathrm{P}(-\sin (\beta-\alpha),-\cos \beta), \mathrm{Q}(\cos (\beta-\alpha), \sin \beta)$ and $\mathrm{R}(\cos (\beta-\alpha+\theta), \sin (\beta-$ $\theta)$ ), where $0<\alpha, \beta, \theta<\frac{\pi}{4}$. Then
(a) P lies on the line segment RQ.
(b) $\mathrm{Q}$ lies on the line segment PR.
(c) $\mathrm{R}$ lies on the line segment $\mathrm{QP}$.
(d) $\mathrm{P}, \mathrm{Q}, \mathrm{R}$ are non-collinear.
Show Answer
Answer: (d)5. The locus of the orthocenter of the triangle formed by the lines $(1+p) x-p y+p(1+p)=0,(1+q) x$ $-q y+(1+q) q=0$ and $y=0$, where $p \neq q$, is
(a) ahyperbola
(b) a parabola
(c) an ellipse
(d) astraight line.
Show Answer
Answer: (d)6. Let points $\mathrm{A}(1,1)$ and $\mathrm{B}(2,3)$. Coordinates of the point $\mathrm{P}$ such that $|\mathrm{PA}-\mathrm{PB}|$ is minimum are
(a) $\left(2, \frac{3}{2}\right)$
(b) $\quad\left(0, \frac{11}{4}\right)$
(c) $(11,3)$
(d) $\left(\frac{3}{2}, 0\right)$
Show Answer
Answer: (b)7. The line $x+7 y=14$ is rotated through an angle $\frac{\pi}{4}$ in the anticlock wise direction about the point $(0$, 2). The equation of the line in its new position is
(a) $3 x-4 y+8=0$
(b) $3 x-4 y-8=0$
(c) $4 x+3 y+8=0$
(d) None of these
Show Answer
Answer: (a)8. If one diagonal of a square is the portion of the line $\frac{x}{a}+\frac{y}{b}=1$ intercepted by the axes, then one to the extremities of the other diagonal of the square are
(A) $\left(\frac{a+b}{2}, \frac{a-b}{2}\right)$
(b) $\left(\frac{a-b}{2}, \frac{a+b}{2}\right)$
(c) $\left(\frac{a-b}{2}, \frac{b-a}{2}\right)$
(d) $\left(\frac{a+b}{2}, \frac{b-a}{2}\right)$
Show Answer
Answer: (c)9. The image of $\mathrm{P}(\mathrm{a}, \mathrm{b})$ in the line $\mathrm{y}=-\mathrm{x}$ is $\mathrm{Q}$ and the image of $\mathrm{Q}$ in the line $\mathrm{y}=\mathrm{x}$ is $\mathrm{R}$, then the midpoint of PR is
(a) $(\mathrm{a}-\mathrm{b}, \mathrm{b}+\mathrm{a})$
(b) $\quad\left(\frac{a+b}{2}, \frac{b+a}{2}\right)$
(c) $\quad(\mathrm{a}-\mathrm{b}, \mathrm{b}-\mathrm{a})$
(d) $\quad(0,0)$
Show Answer
Answer: (d)10. Let $\mathrm{ABC}$ be a triangle. Let $\mathrm{A}$ be the point $(1,2), \mathrm{y}=\mathrm{x}$ is the perpendicular bisector of $\mathrm{AB}$ and $\mathrm{x}-$ $2 \mathrm{y}+1=0$ is the angle bisector of $\angle \mathrm{C}$. If equation of $\mathrm{BC}$ is given by $\mathrm{ax}+\mathrm{by}-5=0$, then $\mathrm{a}+\mathrm{b}$ is
(a) 1
(b) 2
(c) 3
(d) 4










