COORDINATE GEOMETRY - 1 (Straight Line)
Topics covered
1. Slope of a straight line
2. Angle between two lines
3. Special forms of straight lines
(i) Slope and point form
(ii) Two point form
(iii) Slope and y-intercept form
Straight Line
It is a curve such that every point on the line segment joining any two points on it lies on it.
Equation of straight line is always of first degree on $\mathrm{x}$ and $\mathrm{y}$.
General equation of straight line is $a x+b y+c=0$
Where $a, b, c \in R$. a and $b$ can be zero but not both at the same time .
Slope of a line
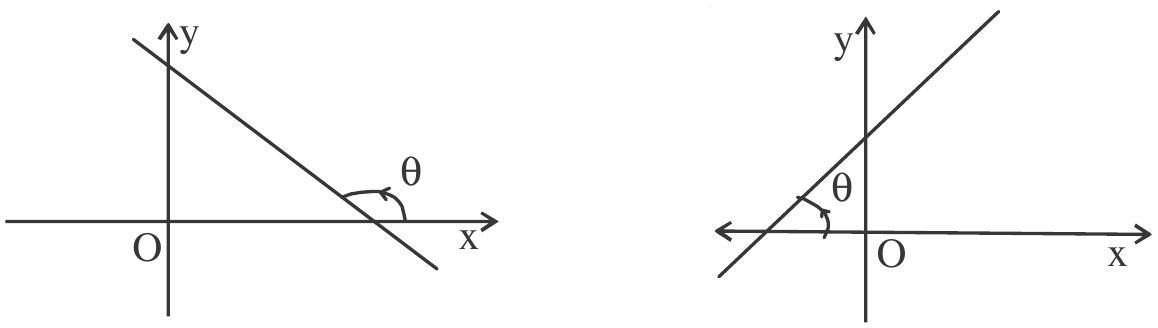
The trigonometrical tangent of an angle that a line makes with the positive direction of the $\mathrm{x}-$ axis in anticlockwise direction is called the slope or gradient of the line
Normally slope is denoted by $\mathrm{m}=\tan \theta$.
Points to remember
(i). Slope of a line parallel to $x$-axis is zero and perpendicular to $x$-a xis is undefined.
(ii). If slope is positive then it makes acute angle with positive direction of $\mathrm{x}$-axis and negative it will make obtuse angle with positive direction of $\mathrm{x}$-axis.
(iii). If a line is equally inclined to the axes, that it will make angle of $45^{\circ}$ or $135^{\circ}$, with $x-$ axis. Hence slope of line is +1 .
(iv). It three points $\mathrm{A}, \mathrm{B}, \mathrm{C}$ are collinear then slope of $\mathrm{AB}=$ slope of $\mathrm{BC}=$ slope of $\mathrm{AC}$
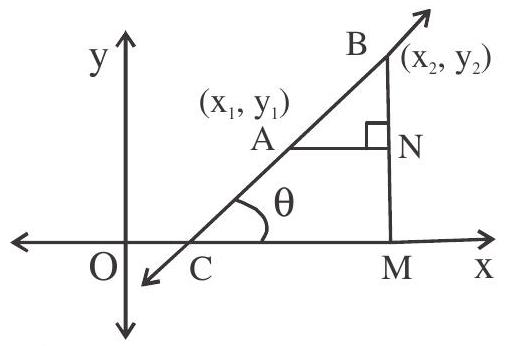
(v). Slope of the line joining two points $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ and $\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right)$ is $\mathrm{m}=\frac{y _{1}-y _{2}}{x _{1}-x _{2}}$ or $\frac{y _{2}-y _{1}}{x _{2}-x _{1}}$
(vi). Equation of $x$-axis is $y=0$
(vii). Equation of $\mathrm{y}$-axis is $\mathrm{x}=0$
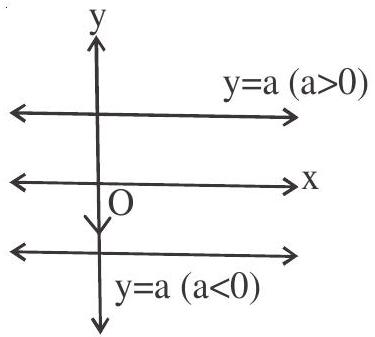
(viii). Equation of line parallel to $\mathrm{x}$-axis is $\mathrm{y}=\mathrm{a}$, where $\mathrm{a}$ is any real number
(ix). Equation of line parallel to $\mathrm{y}$-axis (perpendicular to $\mathrm{x}$-axis) is $\mathrm{x}=\mathrm{a}$, where a is any real number
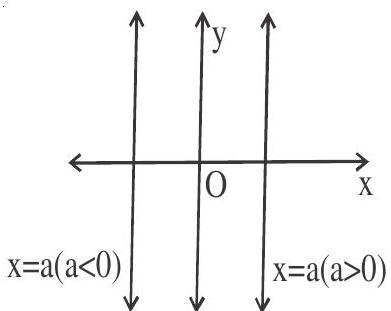
Angle between two lines
The angle $\theta$ between the lines having slopes $m _{1}$ and $m _{2}$ is given by
$ \tan \theta=\left|\frac{\mathrm{m} _{1}-\mathrm{m} _{2}}{1+\mathrm{m} _{1} \mathrm{~m} _{2}}\right|= \pm\left(\frac{\mathrm{m} _{1}-\mathrm{m} _{2}}{1+\mathrm{m} _{1} \mathrm{~m} _{2}}\right) $
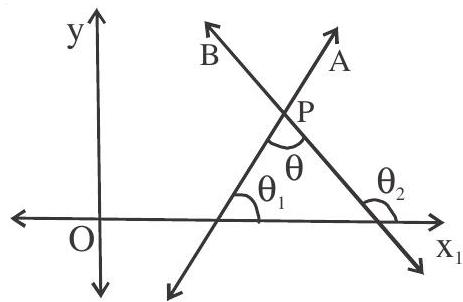
Where $\mathbf{m} _{1}=\tan \theta _{1}, \mathbf{m} _{2}=\tan \theta _{2}$
(i) When two lines are parallel then their slopes are equal ie. $\mathrm{m} _{1}=\mathrm{m} _{2}$
(ii) When two lines are perpendicnlar then the product of their slope is -1
i.e. $\mathrm{m} _{1} \mathrm{~m} _{2}=-1$ or $1+\mathrm{m} _{1} \mathrm{~m} _{2}=0$
A line equally inclined with two lines
Let the two lines with slopes $\mathrm{m} _{1}$ and $\mathrm{m} _{2}$ be equally inclined to a line with slope $\mathrm{m}$ then
$ \left(\frac{m _{1}-m}{1+m _{1} m}\right)=-\left(\frac{m _{2}-m}{1+m _{2} m}\right) $
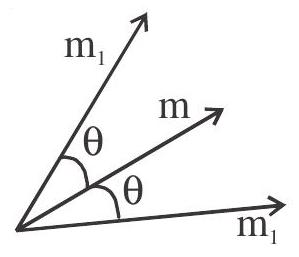
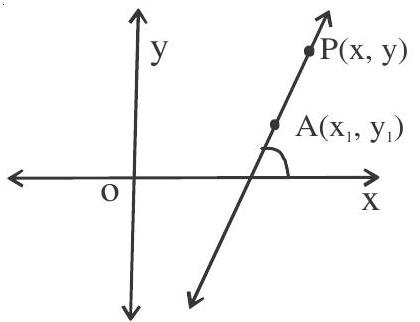
Special form of a line
1. Point slope form
The equation of a line which passes through the point $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ and has the slope $\mathrm{m}$ is $\mathrm{y}-\mathrm{y} _{1}=\mathrm{m}(\mathrm{x}-$ $\mathrm{x} _{1}$ )
2. Two point form
The equation of a line passing through two points $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ and $\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right)$ is $y-y _{1}=\frac{y _{2}-y _{1}}{x _{2}-x _{1}}\left(x-x _{1}\right)$
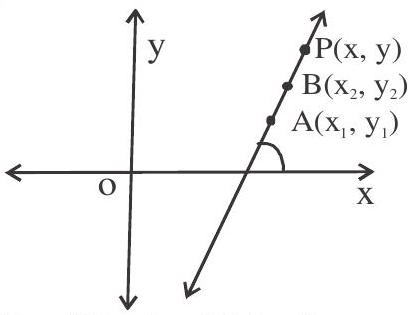
3. Slope and y intercept form [Non Vertical Line]
The equation of a line with slope $m$ that makes an intercept $c$ on $y$-axis is $y=m x+c$

Example:
1. Find the equation of a line that has $y$-intercept -3 and is perpendicular to the line joining (2,3 ) and $(4,2)$.
Show Answer
Solution:
Slope of line joining the points $(2,-3)$ and $(4,2)$ is $\frac{\mathrm{y} _{2}-\mathrm{y} _{1}}{\mathrm{x} _{2}-\mathrm{x} _{1}}=\frac{2+3}{4-2}=\frac{5}{2}$
Since the required line is perpendicular to it
$\therefore$ (slope of the required line) $\mathrm{X}(5 / 2)=-1$
$\therefore$ slope of the required line $=-2 / 5=\mathrm{m}$
$y$-intercept $=-3$
Equation of line is $y=-2 / 5 x-3$
$2 x+5 y+15=0$
Examples
1. If the centroid and circumcentre of a triangle are $(3,3)$ and $(6,2)$ respectively, then the orthocentre is
(a) $(-3,5)$
(b) $(-3,1)$
(c) $(3,-1)$
(d) $(9,5)$
Show Answer
Solution: Centroid, circumcentre and orthocenter are collinear such that centroid divides the circumcentre and orthocentre in the ratio 1:2.
Ans(-3, 5).
2. If the algebraic sum of the perpendicular distances from the point $(2,0),(0,2)$ and $(1,1)$ to a variable straight line be zero, then the line passes through the point
(a) $(3,3)$
(b) $(1,1)$
(c) $(1,-1)$
(d) $(-1,-1)$
Show Answer
Solution:: Let equation be $a x+b y+c=0$
A.T.Q. $\frac{2 a+o b+c}{\sqrt{a^{2}+b^{2}}}+\frac{0+2 b+c}{\sqrt{a^{2}+b^{2}}}+\frac{a+b+c}{\sqrt{a^{2}+b^{2}}}=0$
$\Rightarrow 3 \mathrm{a}+3 \mathrm{~b}+3 \mathrm{c}=0 \Rightarrow \mathrm{a}+\mathrm{b}+\mathrm{c}=0$
This shows that $a x+b y+c=0$ passes through
Ans.$(1,1)$.
3. The area enclosed by $2|x|+3|y| \leq 6$ is
(a) 3 Sq-units
(b) 12 Sq.units
(c) 9 Sq.units
(d) 24 Sq.units
Show Answer
Solution:: $2 x+3 y$
$\leq 6, \quad \mathrm{x} \geq 0, \mathrm{y} \geq 0$
$2 x-3 y \leq 6$,
$\mathrm{x} \geq 0, \mathrm{y} \leq 0$
$-2 x+3 y$
$\leq 6, \quad \mathrm{x} \leq 0, \mathrm{y} \geq 0$
$-2 x-3 y$
$\leq 6, \mathrm{x} \leq 0, \mathrm{y} \leq 0$
Form a rhombus with diagonals 4 & 6 .
Area $=\frac{1}{2} \times 4 \times 6=$
Ans.$12$ sq. units.