COMPLEX NUMBERS AND QUADRATIC EQUATIONS - 1 (Quadratic Equations)
Quadratic equations
The general form of a quadratic equation over real numbers is
Nature of roots : For the quadratic equation

For the quadratic equation

Note 1: If
Note 2:
Relation between roots and coefficients
If
Comparing the coefficients of like powers of
Here
Particular cases :-
Quadratic equation : If
Cubic equation: If
Biquadratic equation : If
Formation of a polynomial equation from given roots
If
Particular cases
Quadratic equation : If
Cubic equation : If
Biquadratic equation : If
ie,
Quadratic Expression : An expression of the form
Graph of a quadratic Expression
Let
Then
Let
Clearly it is the equation of a parabola having its vertex at
If
If
Sign of quadratic Expression
(1) The parabola will intersect the
(i)
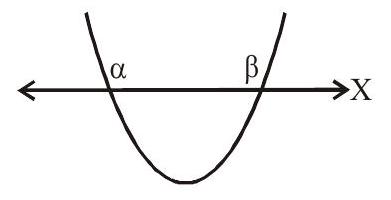
Let
(ii)
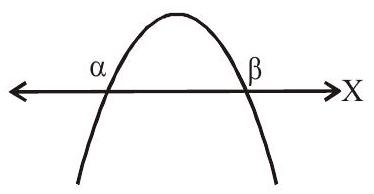
Let
(2) The parabola will touch the

(3) The parabola will not intersect

NOTE : Condition that a quadratic function
NOTE :
(i) For
(ii) For
Solved Examples
1. If
(a).
(b).
(c).
(d). None of these
Show Answer
Solution :
Answer : (a).
2. If
(a). 10, 8
(b). 12, 10
(c). 12, 8
(d). None of these
Show Answer
Solution:
Answer : (c).
3. If
(a).
(b).
(c).
(d). None of these
Show Answer
Solution:
Now
Answer: (c).
4. Let
(a).
(b).
(c).
(d).
Show Answer
Solution :
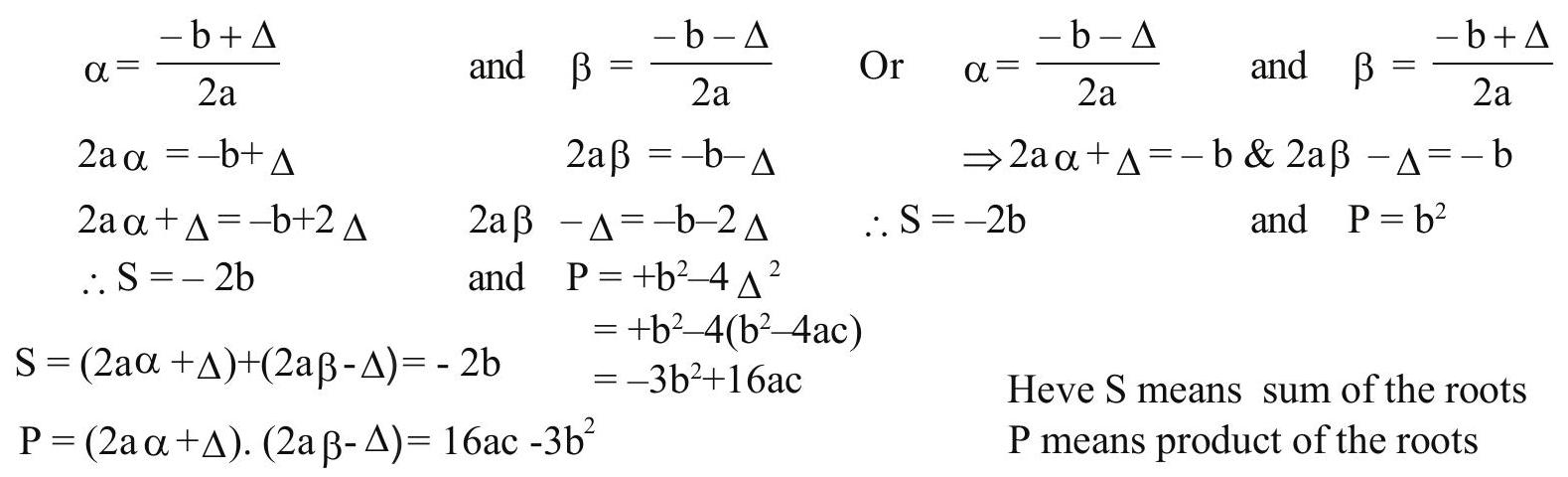
Answer : (a and d)
5. The polynomial equation
(a). four real roots
(b). atleast two real roots
(c). atmost two real roots
(d). No real roots
Show Answer
Solution :
Now
When ac
When ac
Answer: (b).
6. If
(a). 1
(b). 2
(c). 3
(d). None of these
Show Answer
Solution :
Answer: (a).
7. Let
(a). 2
(b). 3
(c). 4
(d). 5
Show Answer
Solution :
Answer : (c).
Practice questions
1. The minimum value of
(a).
(b).
(c).
(d). Non real value of b & c exist
Show Answer
Answer: (b)2. If
(a).
(b).
(c).
(d).
Show Answer
Answer: (b)3. In the quadratic equation
(a).
(b).
(c).
(d).
Show Answer
Answer: (c)4. If
(a).
(b).
(c).
(d).
Show Answer
Answer: (a)5. Let
(a). 1
(b). 2
(c). 3
(d). 4
Show Answer
Answer: (c)6. If
(a). 1210
(b). 1120
(c). 1200
(d). None of these
Show Answer
Answer: (a)7. If
(a).
(b).
(c).
(d).
Show Answer
Answer: (c)8. The curve
(a).
(b).
(c).
(d).
Show Answer
Answer: (c)9. Read the passage and answer the following questions.
Consider the equation
(i) The equation has no real roots if
(a).
(b).
(c).
(d).
Show Answer
Answer: (a, d)(ii) The equation has only two real roots if
(a).
(b).
(c).
(d).
Show Answer
Answer: (d)(iii) The equation has four real roots if
(a).
(b).
(c).
(d).
Show Answer
Answer: (c)10. If
(a).
(b).
(c).
(d). None of these
Show Answer
Answer: (d)11. If
(a).
(b).
(c). for
(d). for
Show Answer
Answer: (a, b, c, d)12. If
(a). 15
(b). 9
(c). 7
(d). 8
Show Answer
Answer: (c)13. In
(a).
(b).
(c).
(d).










