CIRCLE-9 (Co - Axial System of Circles)
Co - Axial System of Circles
A system of circles or family of circles, every pair of which have the same radical axis are called co-axial circles
1. The equation of family of co-axial circles when the equation of radical axis and one circle are given
$\mathrm{L}=\mathrm{ax}+\mathrm{by}+\mathrm{c}=0$
$\mathrm{S} \equiv \mathrm{x}^{2}+\mathrm{y}^{2}+2 \mathrm{gx}+2 \mathrm{fy}+\mathrm{c}=0$
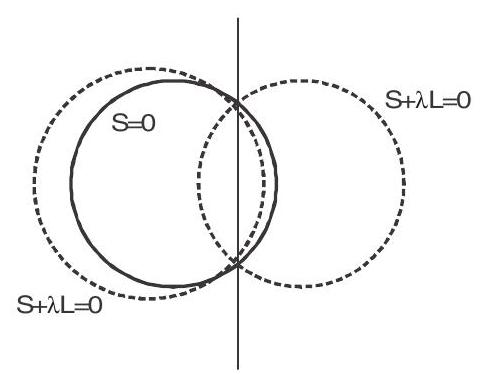
Then equation of co-axial circle is $\mathrm{S}+\lambda \mathrm{L}=0$
2. The equation of co-axial system of a circles where the equation of any two circles of the system are
$\mathrm{S} _{1}=\mathrm{x}^{2}+\mathrm{y}^{2}+2 \mathrm{gx}+2 \mathrm{fy}+\mathrm{c}=0$
$\mathrm{S} _{2}=\mathrm{x}^{2}+\mathrm{y}^{2}+2 \mathrm{~g} _{1} \mathrm{x}+2 \mathrm{f} _{1} \mathrm{y}+\mathrm{c} _{1}=0$
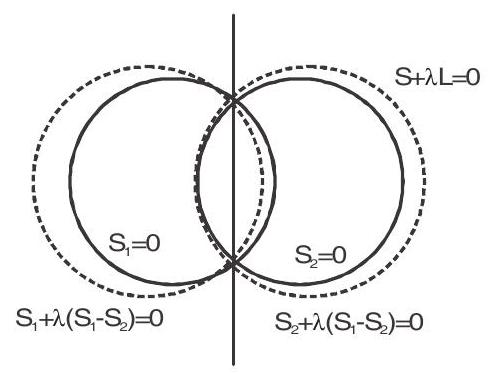
respectively is $\mathrm{S} _{1}+\lambda\left(\mathrm{S} _{1}-\mathrm{S} _{2}\right)=0$
and $\mathrm{S} _{2}+\lambda\left(\mathrm{S} _{1}-\mathrm{S} _{2}\right)=0(\lambda \neq-1)$
$S _{1}+\lambda S _{2}=0(\lambda \neq-1)$
3. The equation of a system of co-axial circles in the simplest form is $\mathrm{x}^{2}+\mathrm{y}^{2}+2 \mathrm{gx}+\mathrm{c}=0$ where $\mathrm{g}$ is variable and $\mathrm{c}$ is a constant
The common radical axis is the $\mathrm{y}$-axis (centre on $\mathrm{x}$-axis)
The equation of system of co-axial circles in the simplest form is $x^{2}+y^{2}+2 f y+c=0$ where $f$ is a variable and $\mathrm{c}$ is a constant
The common radical axis is the $\mathrm{x}$-axis (centre on $\mathrm{y}$ axis)
Examples
1. Find the equation of the system of circles co-axial with the circles $x^{2}+y^{2}+4 x+2 y+1=0$ and $x^{2}+y^{2}-$ $2 x+6 y-6=0$. Also find the equation of that particular circles whose centre lies on radical axis.
Show Answer
Solution:
Given circles are
$ \begin{aligned} & S _{1} \equiv x^{2}+y^{2}+4 x+2 y+1=0 \\ & S _{2} \equiv x^{2}+y^{2}-2 x+6 y-6=0 \\ & S _{1}-S _{2}=0 \\ & 6 x-4 y+7=0 \end{aligned} $
System of co-axial circle is $\mathrm{S} _{1}+\lambda\left(\mathrm{S} _{1}-\mathrm{S} _{2}\right)=0$
$ \begin{aligned} & x^{2}+y^{2}+4 x+2 y+1+\lambda(6 x-4 y+7)=0 \\ & x^{2}+y^{2}+2 x(2+3 \lambda)+2 y(1-2 \lambda)+1+7 \lambda=0 \end{aligned} $
Centre of this circle is $(-(2+3 \lambda),-(1-2 \lambda))$
lies on radical axis
$ \begin{aligned} & \therefore 6(-2-3 \lambda)+4(1-2 \lambda)+7=0 \\ & -12-18 \lambda+4-8 \lambda+7=0 \\ & -1-26 \lambda=0 \\ & \lambda=\frac{-1}{26} \end{aligned} $
$\therefore$ Required particular member of co-axial circle is $26\left(x^{2}+y^{2}\right)+98 x+56 y+19=0$
2. If the circumference of the circle $x^{2}+y^{2}+8 x+8 y-b=0$ is bisected by the circle
$x^{2}+y^{2}-2 x+4 y+a=0$ then $a+b$ equal to
(a) $50$
(b) $56$
(c) $-56$
(d) $-34$
Show Answer
Solution: (c)
Equation of radical axis (common chord of these circles) is $10 x+4 y-b-a=0$
Centre of first circle is $(-4,-4)$
Since second circle bisects the first circle
Therefore centre of first circle must lie on common chord.
$ \begin{array}{ll} \therefore \quad & 10(-4)+4(-4)-b-a=0 \\ & -40-16-(a+b)=0 \end{array} $
$\therefore \quad \mathrm{a}+\mathrm{b}=-56$
3. The equation of the circle passing through the point of intersection of the circles $x^{2}+y^{2}-4 x-2 y=8$ and $x^{2}+y^{2}-2 x-4 y=8$ and the point $(-1,4)$ is
(a) $x^{2}+y^{2}+4 x+4 y-8=0$
(b) $x^{2}+y^{2}-3 x+4 y+8=0$
(c) $x^{2}+y^{2}+x+y-8=0$
(d) $x^{2}+y^{2}-3 x-3 y-8=0$
Show Answer
Solution: (d)
Equation of any circle passing through the point of intersection of the circles is $x^{2}+y^{2}-4 x-2 y-8+\lambda\left(x^{2}+y^{2}-2 x-4 y-8\right)=0$
This circle passes through the point $(-1,4$
$\therefore 1+16+4-8-8+\lambda(1+16+2-16-8)=0$
$5-5 \lambda=0$
$\lambda=1$
Required circle is $x^{2}+y^{2}-3 x-3 y-8=0$
4. If the common chord of the circles $x^{2}+(y-b)^{2}=16$ and $x^{2}+y^{2}=16$ subtends a right angle at the origin then $\mathrm{b}=$
(a) $4$
(b) $4 \sqrt{2}$
(c) $-4 \sqrt{2}$
(d) $8$
Show Answer
Solution:
The equation of common chord is
$\mathrm{S}-\mathrm{S} _{1}=0$
$(\mathrm{y}-\mathrm{b})^{2}-\mathrm{y}^{2}=0$
$\mathrm{b}^{2}-2 \mathrm{by}=0$
$\mathrm{b}(\mathrm{b}-2 \mathrm{y})=0 \quad \mathrm{~b} \neq 0$, so
$\therefore \mathrm{b}=2 \mathrm{y}$ or $1=\frac{2 \mathrm{y}}{\mathrm{b}}$
The combined equation of the straight lines joining the origin to the points if intersection of $\mathrm{y}=\mathrm{b} / 2$ and $\mathrm{x}^{2}+\mathrm{y}^{2}=16\left(\frac{2 \mathrm{y}}{\mathrm{b}}\right)^{2} \Rightarrow \mathrm{b}^{2} \mathrm{x}^{2}+\left(\mathrm{b}^{2}-64\right) \mathrm{y}^{2}=0$
This equation represents a pair of perpendicular lines
$\therefore \mathrm{b}^{2}+\mathrm{b}^{2}-64=0 \Rightarrow \mathrm{b}= \pm 4 \sqrt{2}$
