CIRCLE-8 (Radical axis)
Radical axis
The radical axis of two circles is the locus of a point which moves such that the lengths of the tangents drawn from it to the two circles are equal.
$\mathrm{PT} _{1}=\mathrm{PT} _{2}$
$\mathrm{PT} _{1}=\mathrm{PT} _{2}$
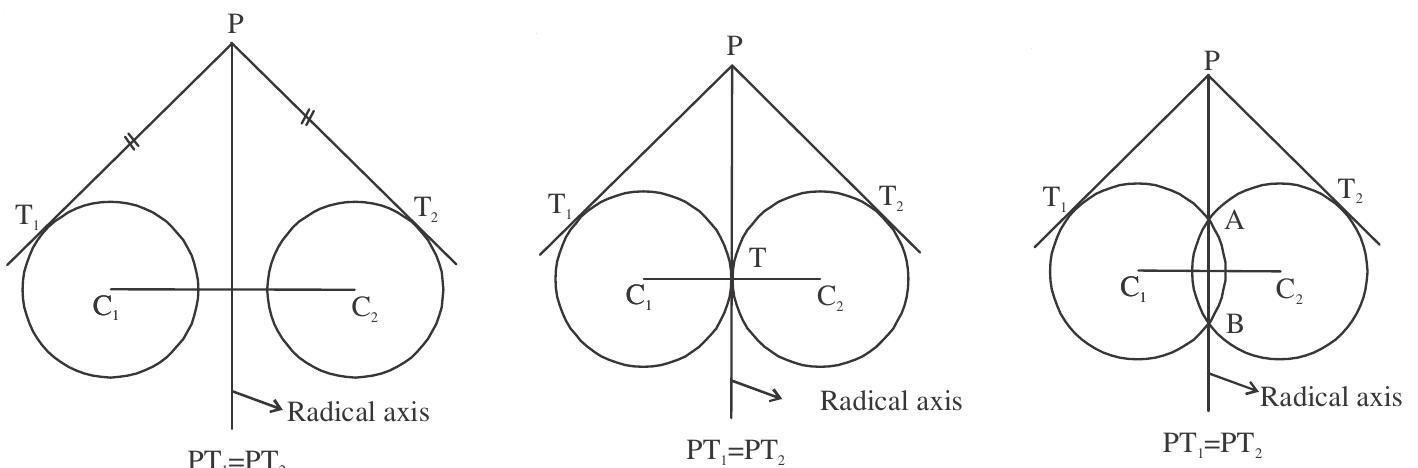
Consider $S=x^{2}+y^{2}+2 g x+2 f y+c=0$ and $S^{\prime}=x^{2}+y^{2}+2 g _{1} x+2 f _{1} y+c _{1}=0$
Let $\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ be any point such that $\left|\mathrm{PT} \mathrm{T} _{1}\right|=\left|\mathrm{PT} _{2}\right|$
or $\quad\left(\mathrm{PT} _{1}\right)^{2}=\left(\mathrm{PT} _{2}\right)^{2}$
$\mathrm{x} _{1}{ }^{2}+\mathrm{y} _{1}{ }^{2}+2 \mathrm{gx} _{1}+2 \mathrm{fy} _{1}+\mathrm{c}=\mathrm{x} _{1}{ }^{2}+\mathrm{y} _{1}{ }^{2}+2 \mathrm{~g} _{1} \mathrm{x} _{1}+2 \mathrm{f} _{1} \mathrm{y} _{1}+\mathrm{c} _{1}$
$2 \mathrm{x} _{1}\left(\mathrm{~g}-\mathrm{g} _{1}\right)+2 \mathrm{y} _{1}\left(\mathrm{f}-\mathrm{f} _{1}\right)+\mathrm{c}-\mathrm{c} _{1}=0(1)$
$\therefore$ locus of $\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ is a straight line and equation (1) represents its equation.
Equation of radical axis is $2 x\left(g-g _{1}\right)+2 y\left(f-f _{1}\right)+c-c _{1}=0$
Properties of radical axis
1. Radical axis is perpendicular to the line joining the centres of the given circles.
(Slope of radical axis) $\times$ slope of line joining centres $=-1$
$\frac{-\left(\mathrm{g}-\mathrm{g} _{1}\right)}{\left(\mathrm{f}-\mathrm{f} _{1}\right)} \times \frac{\mathrm{f}-\mathrm{f} _{1}}{\mathrm{~g}-\mathrm{g} _{1}}=-1$
2. The radical axis bisects common tangents of two circles
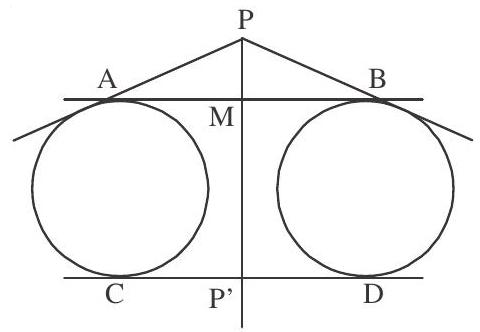
As $\mathrm{M}$ lies on radical axis and $\mathrm{AB}$ is a tangent to the circles $\therefore \mathrm{AM}=\mathrm{BM}$.
Hence radical axis bisects the common tangents
3. If two circles cut a third circle orthogonally, then the radical axis of the two circles will pass through the centre of the third circle, or the locus of the centre of a circle cutting two given circles orthogonally is the radical axis of the given two circles $\mathrm{CP}=\mathrm{CQ}$
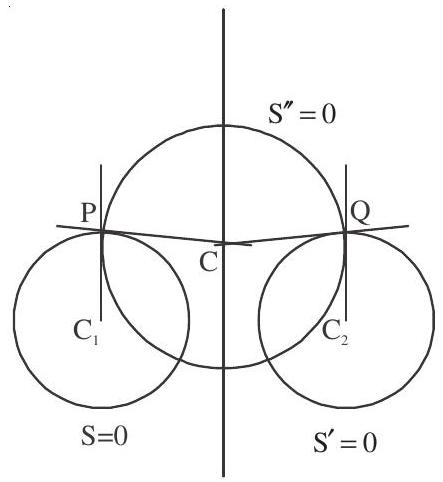
Hence $C$ lies on the radical axis of the circles $S=0$ and $S^{\prime}=0$
4. The position of the radical axis of the two circles geometrically
Radical Centre
The radical axes of three circles, taken in pairs, meet in a point, which is called their radical centre.
Let the three circles be $S _{1}=0, S _{2}=0 S _{3}=0$
OL, OM, ON be radical axes of the pair sets of circles $\left\{S _{1}=0, S _{2}=0\right\},\left\{S _{2}=0, S _{3}=0\right\}$, $\left\{\mathrm{S} _{3}=0, \mathrm{~S} _{1}=0\right\}$ respectively
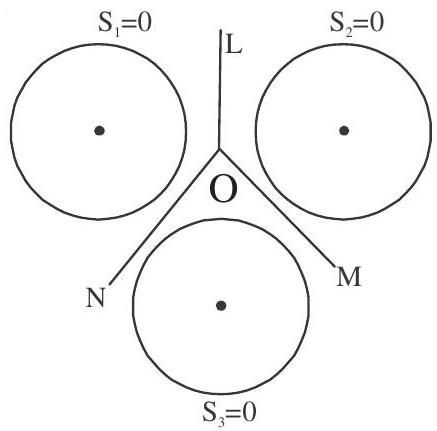
Equations of OL, OM and on are $\mathrm{S} _{1}-\mathrm{S} _{2}=0 \mathrm{~S} _{2}-\mathrm{S} _{3}=0$ and $\mathrm{S} _{3}-\mathrm{S} _{1}=0$
Family of lines passes through point of intersection of lines $S _{1}-S _{2}=0$ and $S _{2}-S _{3}=0$ is
$\mathrm{S} _{1}-\mathrm{S} _{2}+\lambda\left(\mathrm{S} _{2}-\mathrm{S} _{3}\right)=0$
If $\lambda=1$ then the line becomes $S _{3}-S _{1}=0$ $\therefore$ The three lines are concurrent at $\mathrm{O}$
$\mathrm{O}$ is called radical centre .
Properties of radical centre
1. Coordinates of radical centre can be found by solving the equations $S _{1}=S _{2}=S _{3}=0$
2. The radical centre of three circles described on the sides of a triangle as diameters is the orthocenter of the triangle.
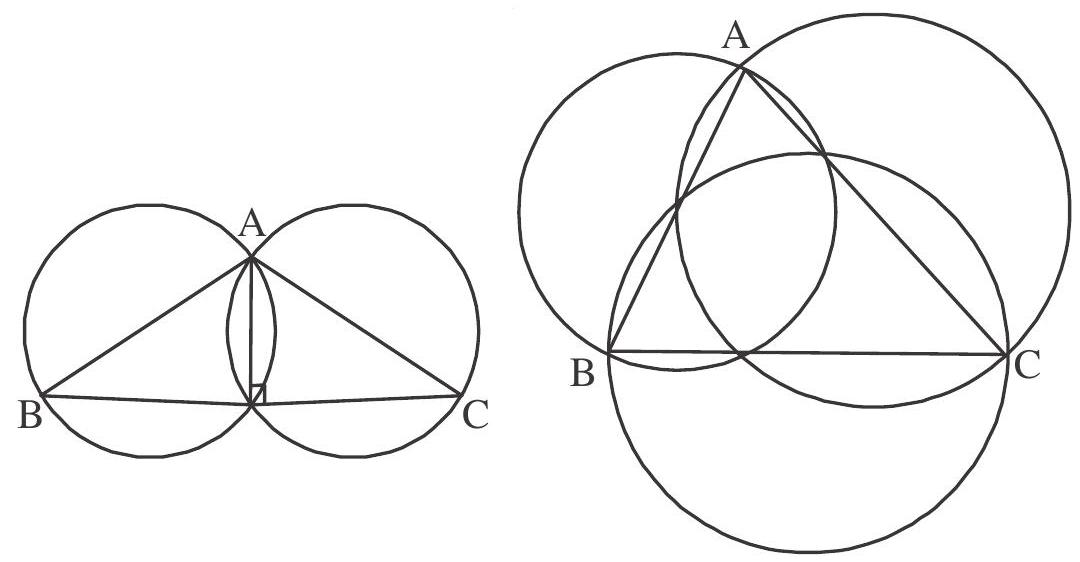
3. The radical centre of three given circles will be the centre of a fourth circle which cuts all the three circles orthogonally. and the radius of the fourth circle is the length of tangent drawn from radical centre of the three given circles to any of these circles
$(\mathrm{x}-\mathrm{y})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2}$ is the fourth circle with centre $(\mathrm{h}, \mathrm{k})$ and radius $\mathrm{r}$
Centre $(h, k)$ is the radical centre of three circles and radius $r$ is the length of tangent to one of these three circles from radical centre $(h, k)$
Examples
1. The equation of the three circles are given $x^{2}+y^{2}=1, x^{2}+y^{2}-8 x+15=0, x^{2}+y^{2}+10 y+24=0$ Determine the coordinates of the point $\mathrm{P}$ such that the tangents drawn from it to the circles are equal in length
Show Answer
Solution: We know that the point from which lengths of tangents are equal in length is radical centre of the given three circles
Radical axis of first two circles is
$\mathrm{S} _{1}-\mathrm{S} _{2}=0$
$8 \mathrm{x}-16=0$ or $\mathrm{x}-2=0$
and radical axis of second and third is
$-8 \mathrm{x}-10 \mathrm{y}-9=0$
Solving (1) and (2) equations we get
$\mathrm{x}=2, \quad-16-10 \mathrm{y}-9=0$
$10 \mathrm{y}=-25$
$\mathrm{y}=\frac{-25}{10}=\frac{-5}{2}$
$\therefore$ Radical centre $\mathrm{P}$ is $(2,-5 / 2)$
2. Find the radical centre of circles $x^{2}+y^{2}+3 x+2 y+1=0, x^{2}+y^{2}-x+6 y+5=0$ and $x^{2}+y^{2}+5 x-8 y+15$ $=0$. Also find the equation of the circle cutting them orthogonally.
Show Answer
Solution :
Let
$ \begin{aligned} & S _{1} \equiv x^{2}+y^{2}+3 x+2 y+1=0 \\ & S _{2} \equiv x^{2}+y^{2}-x+6 y+5=0 \\ & S _{3} \equiv x^{2}+y^{2}+5 x-8 y+15=0 \end{aligned} $
Equations of radical axis
$S_{1}-S_{2}=0 \Rightarrow 4 x-4 y-4=0 \text { or } x-y-1=0 ……{1}$
$S_{2}-S_{3}=0 \Rightarrow-6 x+14 y-10=0 \text { or }-3 x+7 y-5=0 ……{2}$
Solve equations (1) & (2) we get $(3,2)$ as radical centre.
(1) $\times 3-(2) \times 1$
$ \begin{gathered} -3 x+7 y-5=0 \\ -3 x+3 y+3=0 \\ +\quad-\quad- \\ \hline 4 y-8=0 \end{gathered} $
$y=2$
$\mathrm{x}-2-1=0 \Rightarrow \mathrm{x}=3$
radius of fourth circle cutting these three circles orthogonally is length of tangent from this centre to any one circle
$ \begin{aligned} \therefore \mathrm{r} & =\sqrt{\mathrm{S} _{1}} \\ & =\sqrt{3^{2}+2^{2}+3.3+2.2+1} \\ & =\sqrt{9+4+9+4+1} \\ & =\sqrt{27} \\ & =3 \sqrt{3} \end{aligned} $
$\therefore$ Equation of circle is $(\mathrm{x}-3)^{2}+(\mathrm{y}-2)^{2}=(3 \sqrt{3})^{2}$
$ x^{2}+y^{2}-6 x-4 y-14=0 $
3. Find the radical centre of three circles described on the three sides $4 x-7 y+10=0, x+y-5=0$, $7 \mathrm{x}+4 \mathrm{y}-15=0$ of a triangle as diameters.
Show Answer
Solution : We know that radical centre of 3 circles described on the three sides of a triangle as diameters is orthocenter of the triangle.
$\mathrm{L} _{1} \equiv 4 \mathrm{x}-7 \mathrm{y}+10=0$
$\mathrm{L} _{2} \equiv \mathrm{x}+\mathrm{y}-5=0$
$\mathrm{L} _{3} \equiv 7 \mathrm{x}+4 \mathrm{y}-15=0$
Slope of line $L _{1}$ is $4 / 7$ and slope of line $L _{3}=-7 / 4$ since the product of these slopes is -1
$\therefore \mathrm{L} _{1}$ and $\mathrm{L} _{3}$ are perpendicular.
We know that orthocentre of a right angled triangle is the vertex where it has right angle.
Solving (1) & (3) to get orthocentre
$(1) \times 4+(2) \times 7$
$ \begin{aligned} & 16 x-28 y+40=0 \\ & \frac{49 x+28 y-105=0}{65 x-65=0} \\ & x=1 \\ & 4-7 y+10=0 \\ & 7 y+14 \\ & y=2 \end{aligned} $
$\therefore$ Radical centre is $(1,2)$
