CIRCLE-7 (Intersection of Two Circles)
Angle of intersection of two circles
Let the two circles
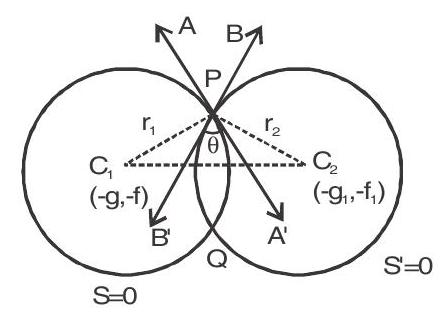
Let
Hence
Now in
If the angle between the circles is
It is a condition for two circles to be orthogonal
Examples :
1. Find the angle between the circles
Show Answer
Solution:
Here
The centre of these circles are
The radius of these circles are
and
Distance between the centres
Angle between two circle is
2. Find the equations of the two circles which intersect the circles
Show Answer
Solution:
Let the required equation of circle be
This circle intersect orthogonally with circles
Condition for orthogonality is
Equation of circle is
Centre is
Since the line
squaring
Hence equations of circles are
3. Prove that the two circles, which pass through
Show Answer
Solution:
Let the equation of the circles be
This circle passes through the points
(1) and
(1) (2)
Centre of this circle is
Since line
Squaring
It is a quadratic in
Sum of roots
Now the equations of the two circles represented are
These two circles will be orthogonal if
But
or
Which is the required condition
4. If the angle of intersection of the circles
Show Answer
Solution:
Let
Also radius these two circles are
and
5. The equation of a circle is
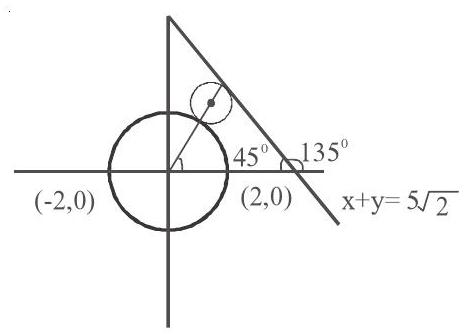
Show Answer
Solution:
Here
The distance of
and
The slope of










