CIRCLE-6 (Tangents and Normals)
1. Director circle and its equation
The locus of the point of intersection of two perpendicular tangents to a given circle is known as its director circle.
Equation of Director Circle
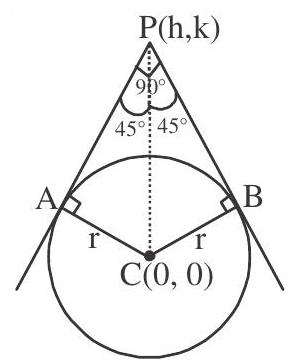
Let
Squaring we get
or
2. Intersection of two circles, common Tangents to two circles
Let the two circles be
with centres
Different cases of intersection of two circles
Case I When
ie., distance between the centre is greater than sum of the radii.
In this case there are 4 common tangents can be drawn.
Two direct common tangents (circles lies on the same side of the tangent)
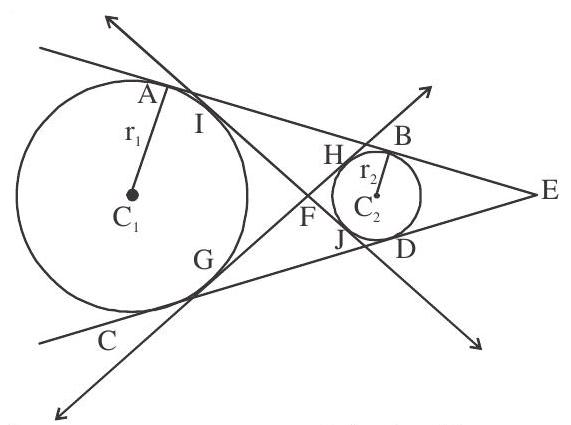
Two indirect (Transverse) common tangents (circles lies opposite side of the tangent) GFH
Note that centres of two circles and point of intersection of tangents are collinear also
To find the equations of common tangents.
Let us assume equation of tangent of any circle in slope form be
Points
Case II When
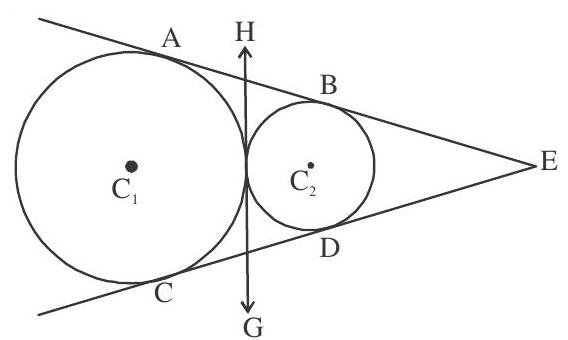
ie., distance between the centre is equal to sum of the radii.
In this case there are 3 common tangents 2 direct common tangent and one transverse common tangent
The equation of tangent at point
Coordinate of
Case III When
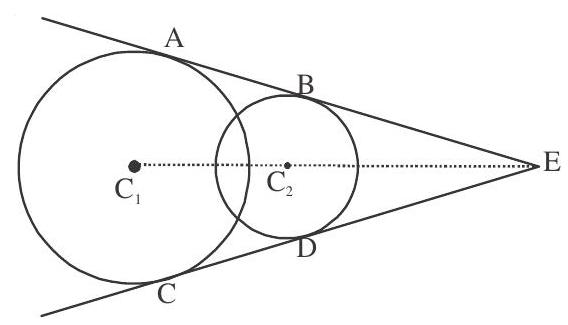
ie,. Distance between the centre is less than sum of the radii.
In this case only two direct common tangents.
Case IV When
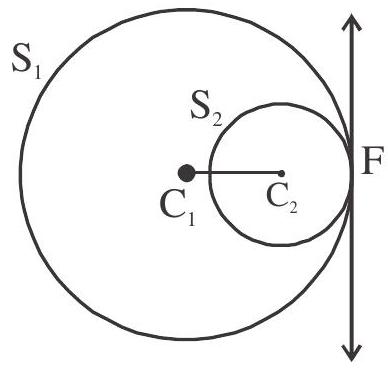 ie., distance between the centre is equal to difference of the radii.
ie., distance between the centre is equal to difference of the radii.
Then the two circles touch each other internally.
In this case only one direct common tangent.
Equation of common tangent is
F divides line joining
Case V When
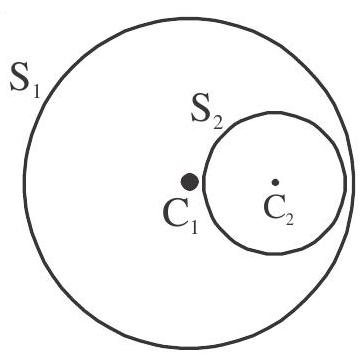
ie., distance between the centre is less than the difference of the radii. Then one circle contains the other
In this case there is no real Common tangents.
3. Length of direct common tangent if
length of direct common tangent
length of transverse common tangent
Where
4. Pole and Polar of the circle
Let
Let the equation of circle be
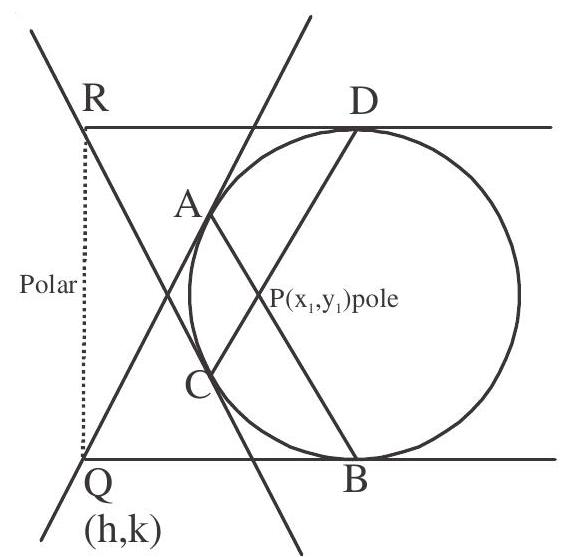
Hence locus of
Coordinates of pole of a line
Let the polar line
Let the pole be
Which is same as ax
comparing (1) and (2) we get
Properties of pole and polar
(i) The distance of any two points
(ii) If
(iii) If
(iv) If the polar of
(v) If the pole of the line
Note:
(i)
(ii) If
5. Common Chord of two circles
The common chord joining the point of intersection of two circles is called their common chord .If
Then equation of common chord
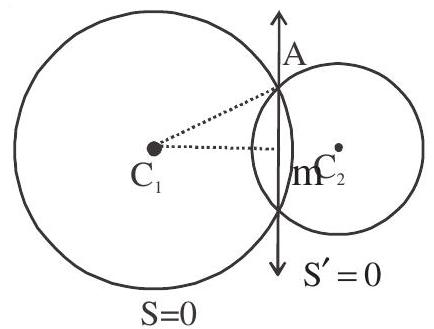
Length of common chord is
Note :
(i) Common chord
(ii) Circle on the common chord a diameter then centre of the circle passing through A and B lie on the common chord of the two circle
(iii) If the length of common chord is zero then the two circles touch each other and the common chord be comes the common tangent to the two circles at the point of contact.
Exercises
1. There are two circles whose equations are
Show Answer
Solution : For
and radius
We know that to get exactly two common tangents the circles must intersect is
or
or
2. Find all the common tangents to the circles
Show Answer
Solution : Centre and radius of circle
To find equations of direct common tangents
Since the coordinate of
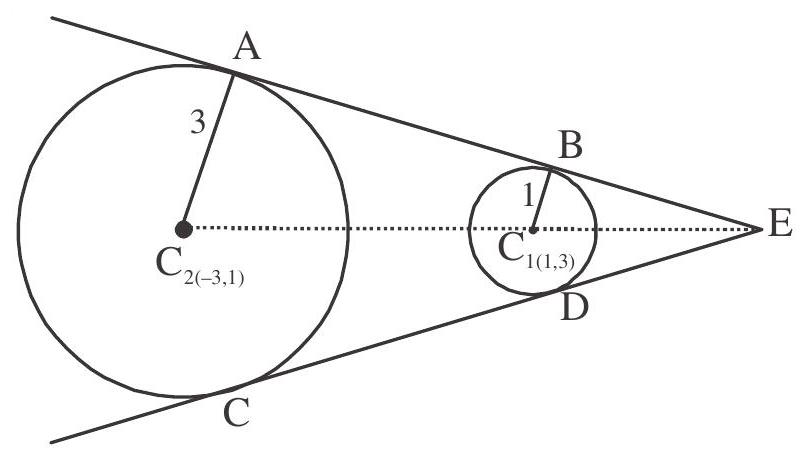
Equation of
If is a tangent to the circle so distance of the line from the centre is equal to radius
Squaring
Substitute the values of
To find the indirect or transverse common tangents
The coordinates of
Equation of line through
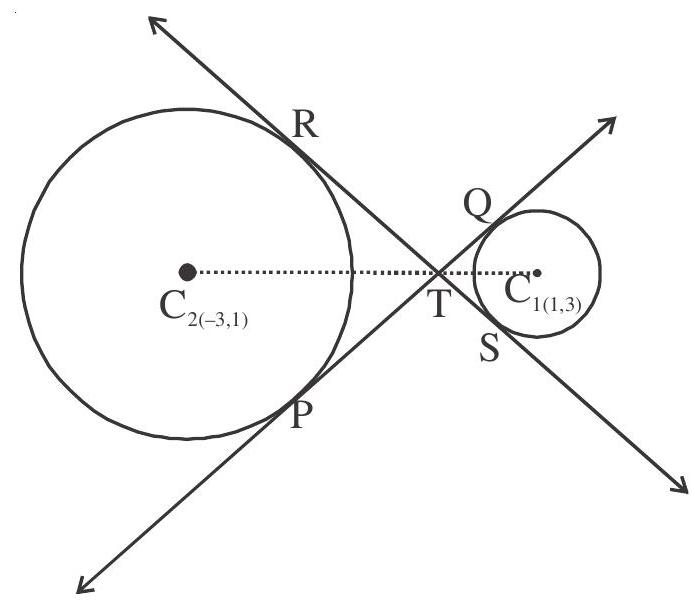
Since it is a tangent to the circles
3. If the circle
Show Answer
Solution:
When two circles intersect, the common chord of maximum length will be the diameter of smaller circle.
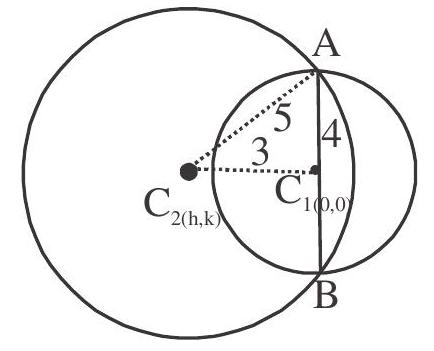
Given that slope of
and slope of
or
Substitute
4. The circle
Show Answer
Solution:
Given circle is
Equation of tangent to the circle at
slope of this line
The circles in old and new positions respectively then
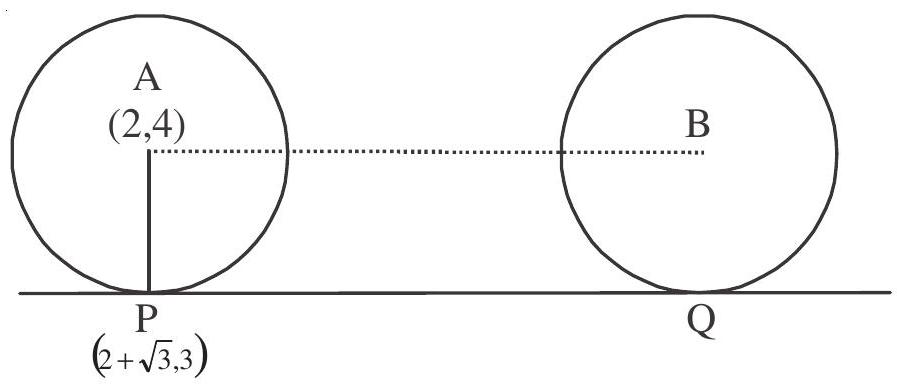
Hence equation of circle at new position is
5. The pole of a straight line with respect to the circle
Prove that the straight line touches the circle
Show Answer
Solution: Let pole be
The equation of the polar with respect to
But given that
If straight line
ie.,
Hence straight line
6. Prove that the polar of a given point with respect to any one of the circles
Show Answer
Solution:
Where
Hence equation (1) represents the family of lines passing through the point of intercection of two lines
Solving equation
Practice questions
Passage 1
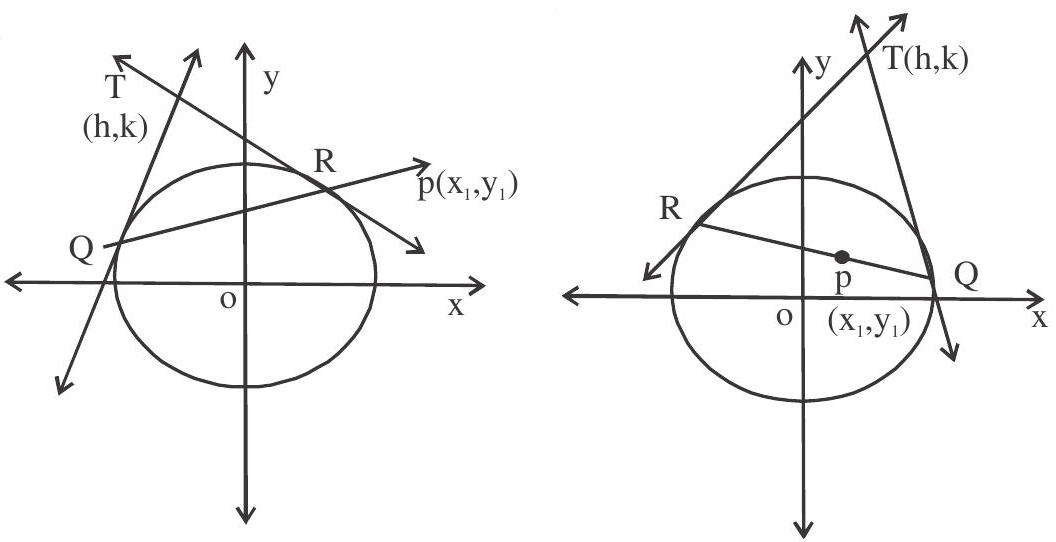
Let a straight line be drawn from a point
Let
Through P, draw a line to meet the circle in Q and R. Let the tangents to the circle at Q and R meet in
It is required to find the polar of Pie., locus of T.
Equation of
since (1) passes through
1. If the polar of
(a)
(c)
(b)
(d) None of these.
Show Answer
Answer: (b)2. The pole of the line
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)3. The pole of the chord of the circle
(a)
(b)
(c)
(d) None of these
Show Answer
Answer: (a)4. The coordinates of the poles of thre common chord of the circles
(a)
(b)
(c)
(d) None of these
Show Answer
Answer: (a)5. The matching grid
| I. The number of common tangents to the circles |
(a). 3 |
| II. The number of common tangents to the circles |
(b). 4 |
| III. The number of common tangents to the circles |
(c). 2 |
| IV. The number of tangents to the circle |
(d). 1 |
Show Answer
Answer:6. If the line
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)7. Two circles of radii
(a)
(b)
(c)
(d) None of these.
Show Answer
Answer: (a)Examples
1. If the tangent at the point
(a) 4
(b)
(c) 5
(d)
Show Answer
Solution. c
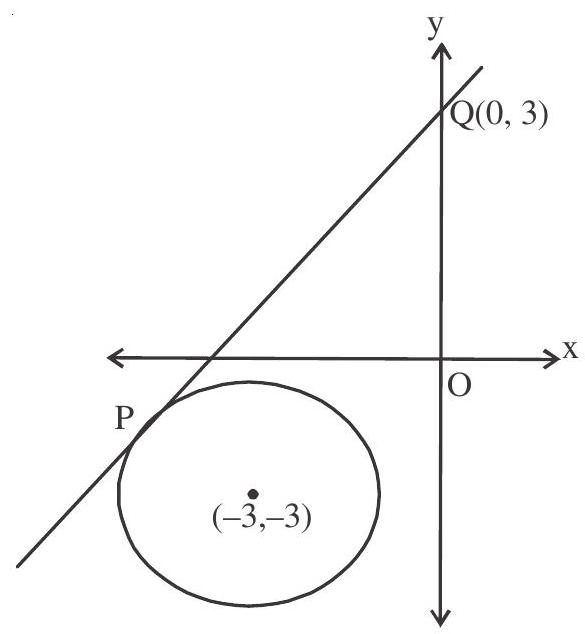
length of tangent
2. If the two circles
(a)
(b)
(c)
(d) None of these
Show Answer
Solution: (a)
Centres of the circles are
or
Squaring both sides

3. The circles
(a)
(b)
(c)
(d) None of these
Show Answer
Solution.
Distance between centres
Distance between










