CIRCLE-5 (Tangents and Normals)
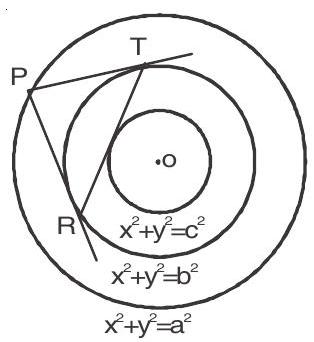
1. Chord of contact
Let the equation of circle be
If the equation of circle be
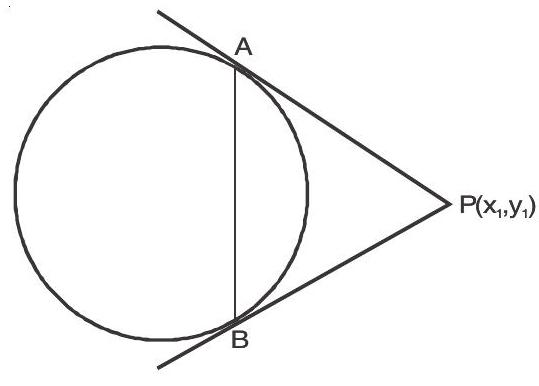
2. Equation of the chord bisected at a given point
Let the equation of circle be
Equation of chord
If the equation of circle be
Examples
1. Find the equation of tangent to the circle
Show Answer
Solution :
Equation of tangent of
2. Find the equations of the tangents to the circle
Show Answer
Solution :
Since tangents make an angle of
radius of circle
we know equation of tangent to a circle
or
3. Show that the line
Show Answer
Solution :
Since the line
Equation of tangent to a circle at
4. Find the equation of the normal to the circle
Show Answer
Solution :
Equation of normal at
Slope of this equation is
Slope of
Since given that normal is parallel to
It is the equation of normal
5. Show that the line
Show Answer
Solution :
Centre and radius of circle
is
If the distance of a line
Let point of contact be
and given line
(1) and (2) are idenfical then comparing (1) and (2) we get
Solving these two equations of
6. The angle between a pair of tangents from a point
Show Answer
Solution :
Let the coordinate of
Distance of
In
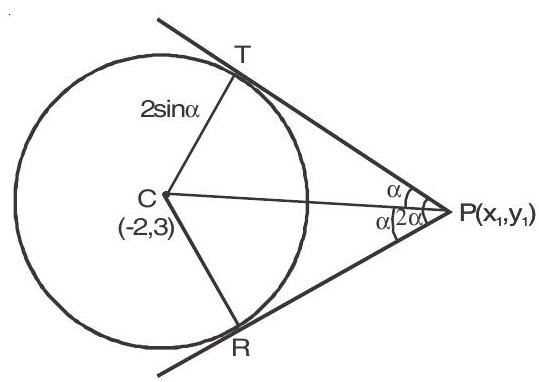
or
Squaring
7. If the length of tangent from (
Show Answer
Solution :
According to the question
Squaring both side
Divide by 3 we get
8. The chord of contact of tangents drawn from a point on the circle
Show Answer
Solution :
Let
It is a tangent to the circle