CIRCLE-4 (Tangents and Normals)
Topics covered :
-
Distance of a line from a circle
-
Different forms of the equations of tangents
-
Length of tangent from a point to a circle.
-
Normal to a circle at a given point.
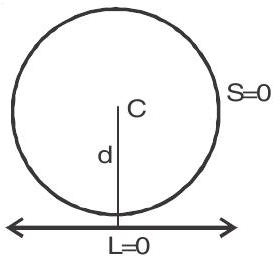
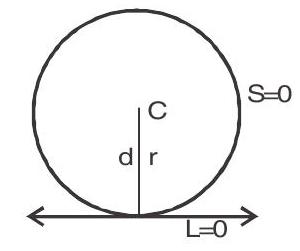
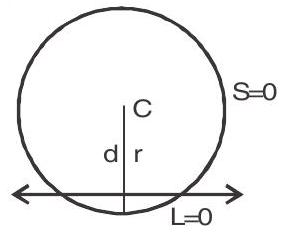
1. Line and a circle
Let
(i)
(ii)
(iii)
(iv)
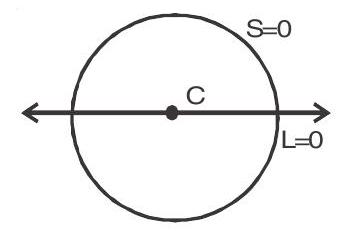
If
(i)
(ii)
(iii)
2. Equations of tangents
1. Point form : Equation of the tangent to the circle
2. Equation of the tangent to the circle
I. Parametric forms
Equation of the tangent to the circle
II. Slope form
The equation of a tangent of slope
The coordinates of the point of contact are
(i) Condition for a line
(ii) Condition that the line
(iii) Equation of tangent to the circle
(iv) The line
(v) If the line
(vi) If the line
III. Tangents from a point outside the circle
If circle is
Squaring
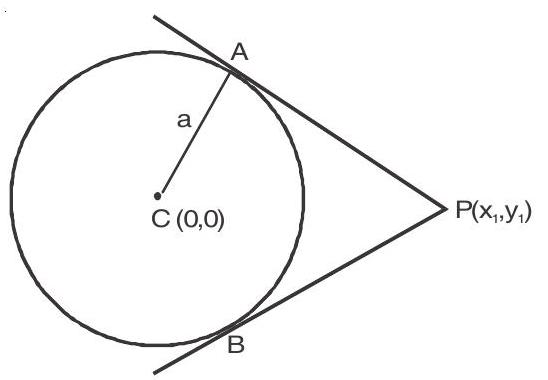
in
We get two equations of tangents.
Tangents from a point outside the circle
Let the circle be
Let the slope of the tangent is
Now find the distance of this line from the centre
IV. Length of the tangent from a point to a circle.
Let the circle be
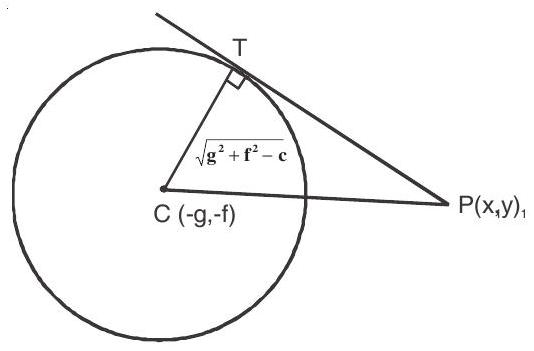
V. Power of point with respect to a circle
The power of
Note :
(i) The power of the point outside the circle is positive
(ii) The power of the point on the circle is zero
(iii) The power of the point inside the circle is negative
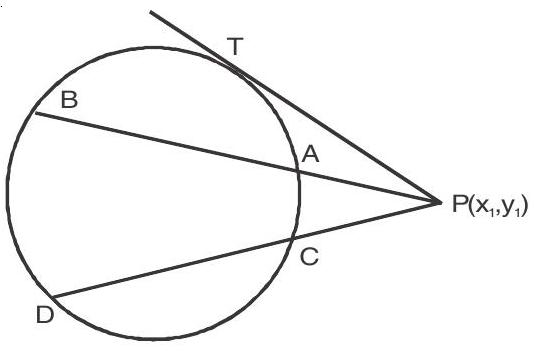
VI. Pair of tangents
The equation of the pair of tangents drawn from the point
Where
Note: The pair of tangents from
VII. Normal to a circle at a given point
The normal of a circle at any point is a straight line which is perpendicular to the tangent at the point and always passes through the centre of the circle.
(1) Point form
To find the equation of normal to the circle
Since we know that normal passes through the centre of a circle. So we get two points on normal using two point form of a line we get the equation of normal as
or
To find normal at
then according to determinant
Write first two rows as ax
Then normal at

- If equation of circle is
- If equation of circle is










