CIRCLE-3 (Problem Solving)
1. The number of points
(a) 90
(b) 81
(c) 80
(d) 69
Show Answer
Solution :
Since
Hence the number of permissible values are
2. A point
(a) Straight line
(b) circle
(c) Parabola
(d) a pair of Straight lines
Show Answer
Solution :
Let two coplanar points be
represents equation of a circle
3. The greatest distance of the point
(a) 10
(b) 15
(c) 5
(d) None of these
Show Answer
Solution :
Given equation of circle in
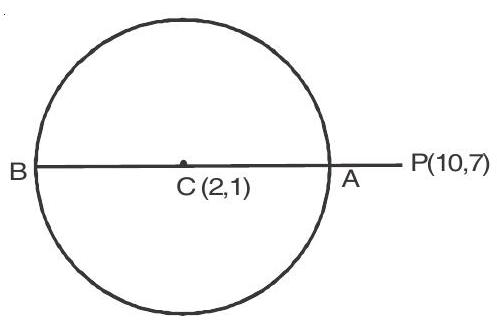
4. If one end of a diameter of the circle
(a)
(b)
(c)
(d)
Show Answer
Solution :
Centre of the circle is
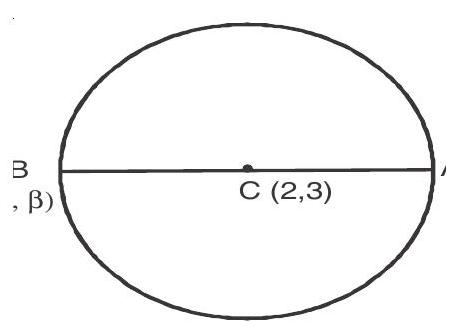
5.
(a)
(b) date are not sufficient
(c)
(d) data are inconsistent
Show Answer
Solution :
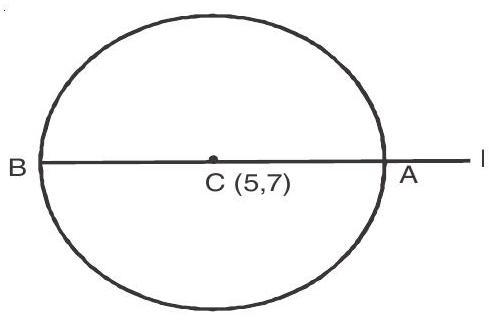
6. If
(a)
(b)
(c) 13
(d) None of these
Show Answer
Solution :
The centre
Examples
7. If
(a) 4
(b) 8
(c) 16
(d) 32 .
Show Answer
Solution :
We know that
(Secant tangent theorem)

8. If
(a)
(b)
(c)
(d)
Show Answer
Solution :
Equation of circle in diameter form
9. If
(a)
(b)
(c)
(d)
Show Answer
Solution :
Centre of the circle is
Radius of the circle is
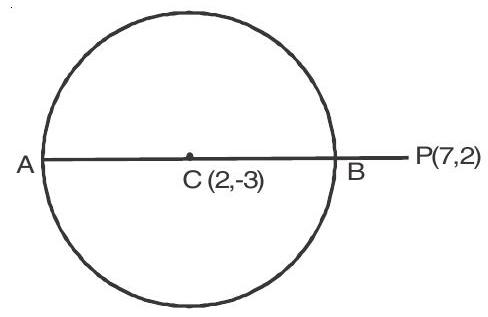
Farthest point
Nearest point
By tinding Point of pnteraction
Practice questions
1. The points
(a) 0
(b) 1
(c) 2
(d) None of these
Show Answer
Answer: (b)2. If the line
(a) a
(b)
(c)
(d)
Show Answer
Answer: (b)3. Equation of incircle of equilateral triangle
(a)
(b)
(c)
(d) None of these
Show Answer
Answer: (a)4. A variable circle having chord of radius ’
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)5. The locus of the centre of the circle which cuts a chord of length 2a from the positive
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)6. The number of circle having radius 5 and passing through the points
(a) one
(b) two
(c) four
(d) infinite
Show Answer
Answer: (b)7. The equation of the smallest circle passing through the intersection of the line
(a)
(b)
(c)
(d) None of these
Show Answer
Answer: (b)8. The number of the points on the circle
(a) 1
(b) 2
(c) 3
(d) None of these
Show Answer
Answer: (d)9. The locus of the mid-point of a chord of the circle
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)10. The area of the triangle formed by joining the origin to the points of intersection of the line
(a) 3
(b) 4
(c) 5
(d) 6
Show Answer
Answer: (c)11. If
(a)
(b)
(c)
(d) None of these
Show Answer
Answer: (b)12. A variable circle passes through the fixed point
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)13. If the lines
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)14. The lines
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)15. The equation of circle which passes through the origin and cuts off intercepts 5 and 6 from the positive parts of the axes respectively, is
(a)
(b)
(c)
(d)










