CIRCLE-2 (Position of a Point)
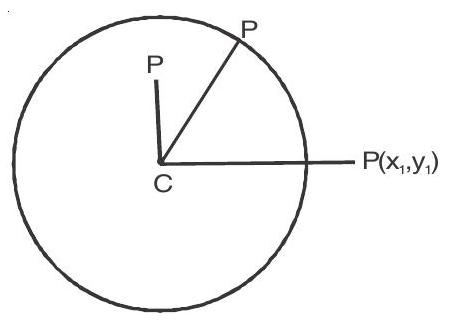
1. Position of a point with respect to a circle .
let the circle is $x^{2}+y^{2}+2 g x+2 f y+c=0$
Point $\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ lies outside, on or inside the circle accordingly $\mathrm{CP}>$, $=$, $<$ radius
(or) $\mathrm{S} _{1}=\mathrm{x} _{1}{ }^{2}+\mathrm{y} _{1}{ }^{2}+2 \mathrm{gx} _{1}+2 \mathrm{fy} _{1}+\mathrm{c}>,=,<0$
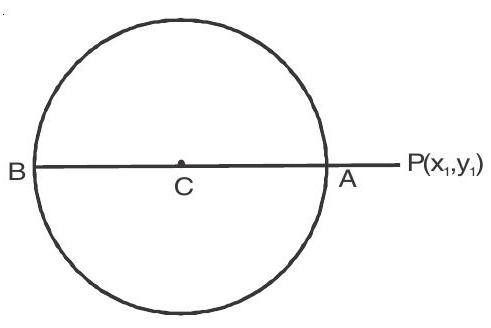
2. Maximum and minimum distance of a point from the circle
Let the circle $x^{2}+y^{2}+2 g x+2 f y+c=0$ and point $P\left(x _{1}, y _{1}\right)$
The maximum and minimum distance form $\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ to the circle are
$\mathrm{PB}=\mathrm{CB}+\mathrm{CP}$
$=\mathrm{r}+\mathrm{CP}$
$\mathrm{PA} \quad=|\mathrm{CP}-\mathrm{CA}|=|\mathrm{PC}-\mathrm{r}|$
$\mathrm{PB}$ is maximum distance and $\mathrm{PA}$ is minimum distance.
Examples
1. If the equation $p x^{2}+(3-q) x y+2 y^{2}-6 q x+30 y+6 q=0$ represents a circle, then the values of $p$ and q are
(a) 3, 1
(b) 2, 2
(c) 2, 3
(d) 3, 4
Show Answer
Solution :
$\mathrm{ax}^{2}+\mathrm{by}^{2}+2 \mathrm{hxy}+2 \mathrm{gx}+2 \mathrm{fy}+\mathrm{c} 0$
represents a circle if $\mathrm{h}=0$ and $\mathrm{a}=\mathrm{b}$
$\therefore \mathrm{p}=2$ and $3-\mathrm{q}=0 \Rightarrow \mathrm{q}=3$
Correct option is :(c)
2. The number if integral values of $\lambda$ for which $x^{2}+y^{2}+(1-\lambda) x+\lambda y+5=0$ is the equation of a circle whose radius cannot exceed 5 is
(a) 20
(b) 16
(c) 18
(d) 24
Show Answer
Solution :
radius of the equation $\sqrt{\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}}$
$g=\frac{1-\lambda}{2}, \quad f=\frac{\lambda}{2} \quad c=5$
$\sqrt{\left(\frac{1-\lambda}{2}\right)^{2}+\frac{\lambda^{2}}{4}-5} \leq 5$
$1+\lambda^{2}-2 \lambda+\lambda^{2}-20 \leq 300$
$2 \lambda^{2}-2 \lambda-119 \leq 0$
$ \begin{aligned} & D=4+8 \times 119 \\ & =4+952 \\ & =956 \\ & =4(239) \\ & \lambda=\frac{2 \pm 2 \sqrt{239}}{4} \\ & =\frac{1-\sqrt{239}}{2} \frac{1+\sqrt{239}}{2} \\ & \therefore \frac{1-\sqrt{239}}{2} \leq \lambda \leq \frac{1+\sqrt{239}}{2} \\ & -7.2 \leq \lambda \leq 8.2 \text { (approx) } \\ & \lambda=-7,-6,-5,-4, \ldots \ldots . .8 \end{aligned} $
number of values of $\lambda$ is 16
3. The equation of the circle which passes through $(1,0)$ and $(0,1)$ and has its radius as small as possible is
(a) $x^{2}+y^{2}-2 x-2 y+1=0$
(b) $x^{2}+y^{2}-x-y=0$
(c) $2 x^{2}+2 y^{2}-3 x-3 y+1=0$
(d) $x^{2}+y^{2}-3 x-3 y+2=0$
Show Answer
Solution :
The radius will be minimum, if the given points are the end points of a diameter. Then the equation of the circle is $(x-1)(x-0)+(y-0)(y-1)=0 \Rightarrow x^{2}+y^{2}-x-y=0$
4. The centre of the circle $x=-1+2 \cos \theta, y=3+2 \sin \theta$ is
(a) $(1,-3)$
(b) $(-1,3)$
(c) $(1,3)$
(d) None of these
Show Answer
Solution :
Rewrite the given equation
$\begin{array}{ll}x+1=2 \cos \theta & y-3=2 \sin \theta \\ \frac{x+1}{2}=\cos \theta & \frac{y-3}{2}=\sin \theta\end{array}$
squaring and adding
$ \begin{aligned} & \left(\frac{x+1}{2}\right)^{2}+\left(\frac{y-3}{2}\right)^{2}=\cos ^{2} \theta+\sin ^{2} \theta \\ & (x+1)^{2}+(y-3)^{2}=4 \\ & \text { centre }(-1,3) \text { radius } 2 \end{aligned} $
