CIRCLE-11 (Problem Solving)
Examples
1. Find the equation of the image of the circle
Show Answer
Solution :
The given circle and line are
(1) and
Centre and radius if the circle are
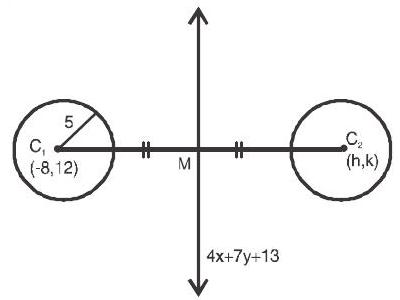
Equation of line
Equation of line
To get the coordinates of M. Solve the equation
(2) & (3)
(2)
put the value of
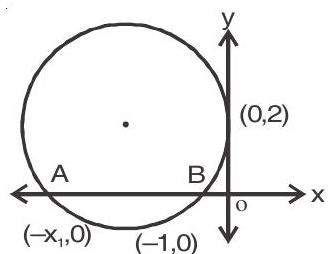
2. The circle passing through the point
(a)
(b)
(c)
(d)
Show Answer
Solution:
Family of circles passing through a point
It passes through
If also passes through
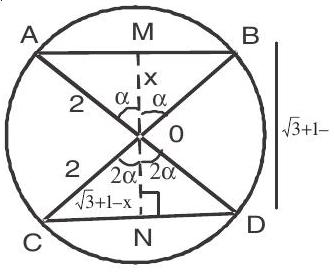
3. Two parallel chords of a circle of radius 2 are at a distance
(
Show Answer
Solution:
Let
Then
In
In
4. Let
Show Answer
Solution:
Draw circle through
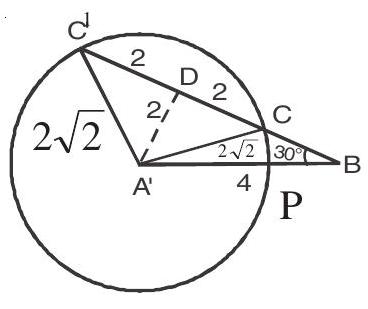
Difference of areas of
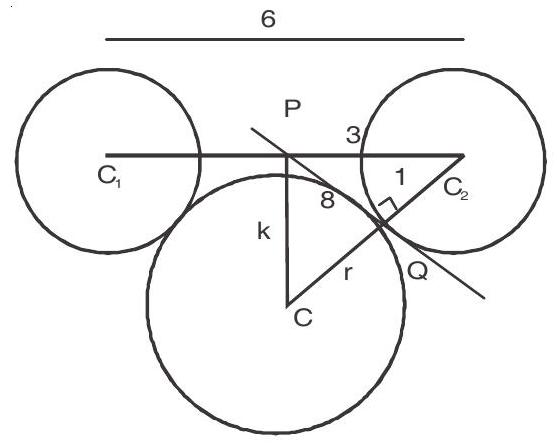
5. The centres of two circles
Show Answer
Solution :
In
In
From (1) & (2)
6. A straight line through the vertex
(a)
(b)
(c)
(d)
Show Answer
Solution :
Points P, Q, T, R are concyclic
and
Also,
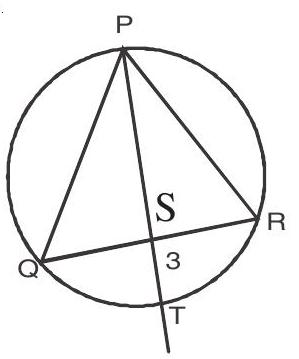
(Dividing by PS.ST)
7. Let
(a)
(b)
(c)
(d)
Show Answer
Solution :
ar
It is a tangent to the circle
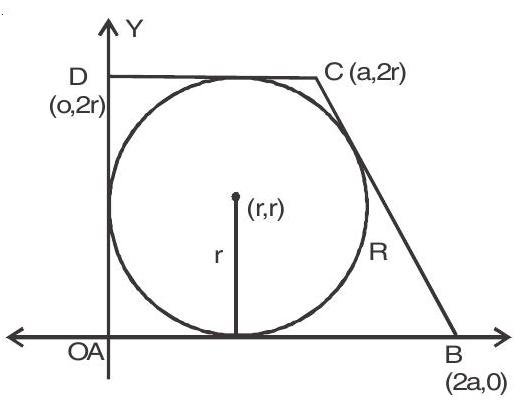
Squaring
ar
8. The radius of the least circle passing through the point
(a)
(b)
(c)
(d)
Show Answer
Solution :
Let the circle be
Given circle is
These two circles are orthogonal
(1) passes through
radius
For least circle radius must be minimum
Let
Equation of circle in
radius
9.
(a)
(b)
(c)
(d)
Show Answer
Solution :
Equation of the two circles be
These two circles passes through
It is a quadratic equation in
Condition for orthogonality is
10. A circle
(a) area of
(b) radius of director circle of
(c) Radius of director circle of
(d)
Show Answer
Solution :
passion through
(1) - (2) we get
radius
for minimum area radius must be minimum
Since
Area
Radius of director circle is
11. Area of part of circle
Show Answer
Solution :
Since line
passes through the centre
Hence

Practice questions
1. Let
(a). clockwise rotation around origin through an angle
(b). anti-clockwise rotation around origin through an angle
(c). reflection in the line through origin with slope
(d). reflection in the line through origin with slope tan
Show Answer
Answer: (d)2. If the tangent at the point
(a). 4
(b).
(c). 5
(d).
Show Answer
Answer: (c)3. The equations to the sides
(a). centroid of the triangle
(b). orthocenter
(c). circumcentre
(d). incentre
Show Answer
Answer: (b)4. The number of rational point(s) (a point
(a). at most one
(b). at least two
(c). exactly two
(d). infinite
Show Answer
Answer: (a)5. The locus of a point such that the tangents drawn from it to the circle
(a).
(b).
(c).
(d).
Show Answer
Answer: (a)6. If the two circles
(a).
(b).
(c).
(d). none of these
Show Answer
Answer: (a)7. The number of integral values of
(a). 14
(b). 18
(c). 16
(d). none of these
Show Answer
Answer: (c)8. The circle
(a). 3
(b). 4
(c). 7
(d). 1
Show Answer
Answer: (d)9. One of the diameter of the circle
(a).
(b).
(c).
(d).
Show Answer
Answer: (b)10. The coordinates of the middle point of the chord cut off by
(a).
(b).
(c).
(d).
Show Answer
Answer: (a)11. A variable chord is drawn through the origin to the circle
(a).
(b).
(c).
(d).
Show Answer
Answer: (c)12. If
(a).
(b).
(c).
(d). none of these
Show Answer
Answer: (d)13. Equation of the normal to the circle
(a).
(b).
(c).
(d).
Show Answer
Answer: (b)14. The equation of the circle touching the lines
(a).
(b).
(c).
(d). none of these
Show Answer
Answer: (a)15. The shortest distance from the point
(a). 1
(b). 2
(c). 3
(d). 4
Show Answer
Answer: (b)16. The equation of the image of the circle
(a).
(b).
(c).
(d).
Show Answer
Answer: (d)17. If
(a).
(b).
(c).
(d).
Show Answer
Answer: (b)18. A circle of the coaxial system with limiting points
(a).
(b).
(c).
(d).
Show Answer
Answer: (d)19. If a variable circle touches externally two given circles, then the locus of the centre of the variable circle is
(a). a straight line
(b). a parabola
(c). an ellipse
(d). a hyperbola
Show Answer
Answer: (d)Passage - 1
Let
On the basis of above information, answer the following questions:
20. If
(a). a straight line
(b). a circle
(c). a parabola
(d). an ellipse
Show Answer
Answer: (b)21. If
(a). a straight line
(c). a circle
(c). a parabola
(d). a hyperbola
Show Answer
Answer: (a)22. If
(a). A lies inside the circle and
(b). A lies outside the circle and
(c). both
(d). both
Show Answer
Answer: (a)23. If
(a). A lies outside the circle and
(b). A lies outside the circle and
(c). both
(d). both
Show Answer
Answer: (b)24. If focus of
(a). passes through
(b). never passes through
(c). passes through
(d). passes through B but does not pass through A
Show Answer
Answer: (b)Passage - 2
For each natural number
On the basis of above information, answer the following questions:
25. Let,
(a). 3
(b). 5
(c). 7
(d). 8
Show Answer
Answer: (c)26. If
(a).
(b).
(c).
(d).
Show Answer
Answer: (c)27. If and , the particle moves in the radial direction from circle
(a). it will cross the + ve
(b). it will cross the - ve
(c). it will cross the + ve
(d). it will cross the - ve
Show Answer
Answer: (c)28. If and , particle moves tangentially form the circle
(a). the particle will cross
(b). the particle will cross
(c). the particle will cross +ve
(d). the particle will cross +ve
Show Answer
Answer: (d)29. Let the particle starts from the point
(a).
(b).
(c).
(d).
Show Answer
Answer: (a)Match Type:
30. Observe the following columns:
| Columns I | Columns II |
|---|---|
| (a). If the shortest and largest distance from the point |
p. |
| (b). If the shortest and largest distance from the point |
q. |
| (c). If the shortest and largest distance from the point |
r. |
| s. |
|
| t. |
Show Answer
Answer: a31. Observe the following columns:
| Columns I | Columns II |
|---|---|
| (a). If the straight lines |
p. |
| (b). If the chord of contact of the tangents drawn to touches the circle |
q. |
| (c). If the circles |
r. |
| s. |
|
| t. |










