Basic concepts

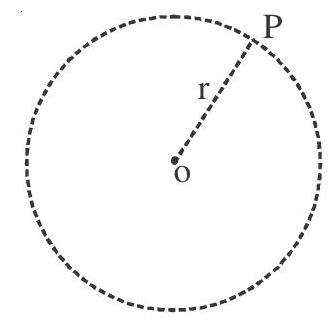
Circle : A circle is the locus of points which are equidistant from a fixed point and lies on the same plane.

Fixed point is called centre of a circle and constant distance is called radius of the circle

Standard equation of a circle

The equation of a circle with the centre at $(\mathrm{h},\mathrm{k})$ and radiaus $\mathrm{r}$ is

$(\mathrm{x}-\mathrm{h}{)}^2+(\mathrm{y}-\mathrm{k}{)}^2={\mathrm{r}}^2$

If centre is at the origin and radius is $r$ then the equation of circle is $x^2+y^2$ $={\mathrm{r}}^2$

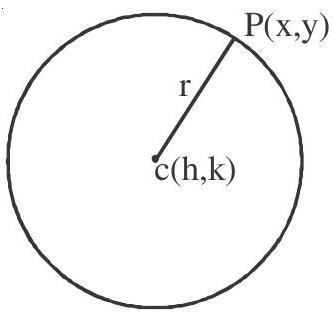
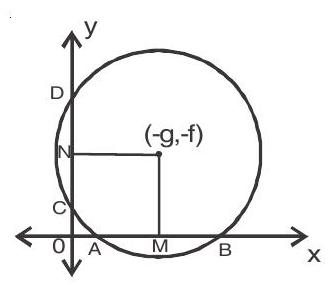
General equation of a circle

$x^2+y^2+2gx+2fy+c=0$ where $g,f$, and $c$ are constants

centre ( $-\mathrm{g},-\mathrm{f})$ and radius is $\sqrt{{\mathrm{g}}^2+{\mathrm{f}}^2-\mathrm{c}}$

Conditions for a second-degree equation to represent a circle

$a^2+2hxy+b{y}^2+2gx+2fy+c=0$ is a second degree equation

(i) coefficient of ${\mathrm{x}}^2=$ coefficient of ${\mathrm{y}}^2.$ ie., $\mathrm{a}=\mathrm{b}$

(ii) coefficient of $xy=0$ ie., $\mathrm{h}=0$

If ${\mathrm{g}}^2+{\mathrm{f}}^2-\mathrm{c}>0$ then the circle represents real circle with centre $(-\mathrm{g},-\mathrm{f})$

If ${\mathrm{g}}^2+{\mathrm{f}}^2-\mathrm{c}=0$ then the circle represents point circle since radius is zero

If ${\mathrm{g}}^2+{\mathrm{f}}^2-\mathrm{c}<0$ then the circle is imaginary circle .

Equation of circle in various forms

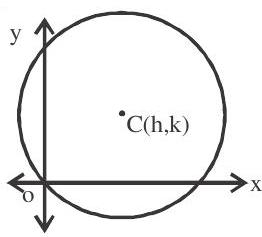
1. Equation of circle with centre (h.k) and passes through origin. is $x^2+y^2+2hx+2ky=0$

Note that when a circle passes through origin the constant term must be zero

2. If the circle touches $\mathrm{x}$-axis then its equation is $(\mathrm{x}\pm \mathrm{h}{)}^2+(\mathrm{y}\pm \mathrm{k}{)}^2={\mathrm{k}}^2(\mathrm{or}){\mathrm{x}}^2+{\mathrm{y}}^2\pm 2\mathrm{hx}\pm 2\mathrm{ky}+{\mathrm{h}}^2=0$. In this case radius is ordinate of centre of a circle. Four circles possible

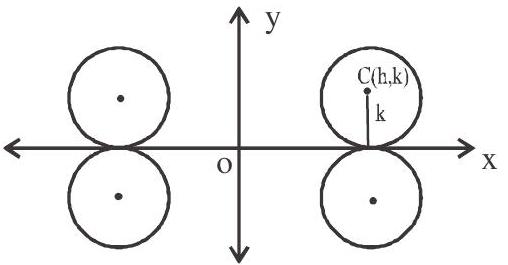
3. If the circle touches $y$-axis then its equation is $(x\pm h{)}^2+(y\pm k{)}^2=h^2($ or $)x^2+y^2\pm 2hx\pm 2ky+k^2$ $=0$. Here radius of the circle is abscissa of the centre. Four circles possible.

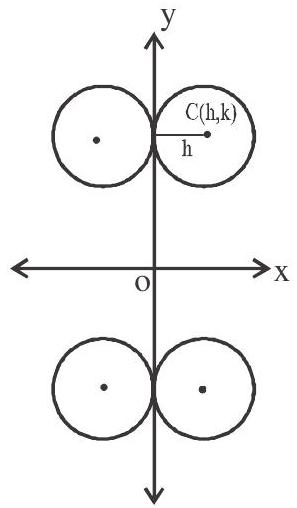
4. If the circle touches both the axes then its equation is $(x\pm r{)}^2+(y\pm r{)}^2=r^2$. Four circles possible ${\mathrm{x}}^2+{\mathrm{y}}^2\pm 2\mathrm{rx}\pm 2\mathrm{ry}+{\mathrm{r}}^2=0$

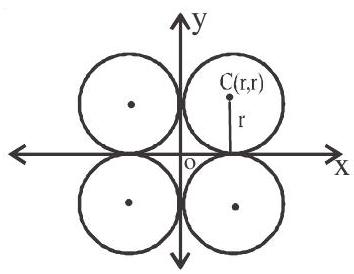
5. If the circle touches $x$-axis at origin then its equation is $x^2+(y\pm k{)}^2=k^2$

${\mathrm{x}}^2+{\mathrm{y}}^2\pm 2\mathrm{ky}=0$

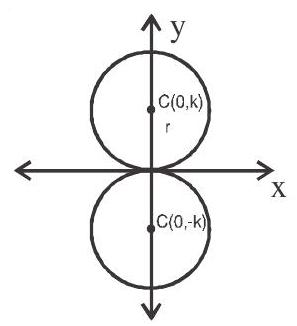
6. If the circle touches $y$-axis at origin then its equation is $(x\pm h{)}^2+y^2=h^2(or)x^2+y^2\pm 2hx=0$

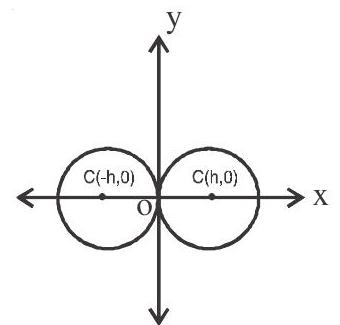
7. If the circle passes through origin and cuts intercepts $a$ and $b$ on the axes, then the equation of circle is ${\mathrm{x}}^2+{\mathrm{y}}^2-\mathrm{ax}-\mathrm{by}=0$ and centre is $\mathrm{c}(\mathrm{a}/2,\mathrm{b}/2)$ four circles possible.

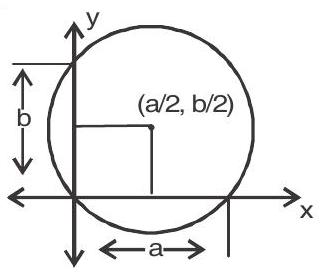
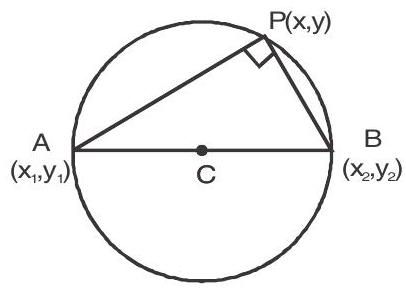
Equation of circle on a given diameter

8. If $({\mathrm{x}}_1,{\mathrm{y}}_1)$ and $({\mathrm{x}}_2,{\mathrm{y}}_2)$ are end points of the diameter then the equation of circle is $(\mathrm{x}-{\mathrm{x}}_1)(\mathrm{x}-{\mathrm{x}}_2)+(\mathrm{y}-{\mathrm{y}}_1)(\mathrm{y}-{\mathrm{y}}_2)=0$

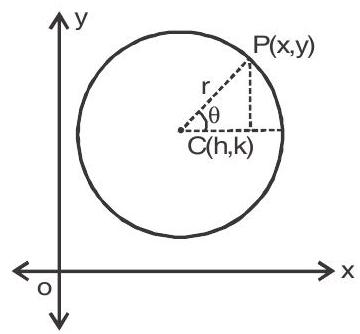
Parametric form of circle

9. $\mathrm{x}=\mathrm{h}+\mathrm{r}\cos \theta$

$\mathrm{y}=\mathrm{k}+\mathrm{r}\sin \theta$

Where $\theta$ is parameter $(0\le \theta \le 2\pi )$

In particular coordinates of any point on the circle ${\mathrm{x}}^2+{\mathrm{y}}^2={\mathrm{r}}^2$ is $(\mathrm{r}\cos \theta ,r\sin \theta )$ on the circle ${\mathrm{x}}^2+{\mathrm{y}}^2+2\mathrm{gx}+2\mathrm{fy}+\mathrm{c}=0$ is $(-\mathrm{g}+\sqrt{{\mathrm{g}}^2+{\mathrm{f}}^2-\mathrm{c}}(\cos \theta ),-f+\sqrt{{\mathrm{g}}^2+{\mathrm{f}}^2-\mathrm{c}}(\sin \theta ))$

Intercept made on the axes by a circle

10. Let the equation of circle is $x^2+y^2+2gx+2fy+c=0$

$\mathrm{AB}=\mathrm{x}-$ intercept $=2\sqrt{{\mathrm{g}}^2-\mathrm{c}}$

$\mathrm{CD}=\mathrm{y}-$ intercept $=2\sqrt{{\mathrm{f}}^2-\mathrm{c}}$