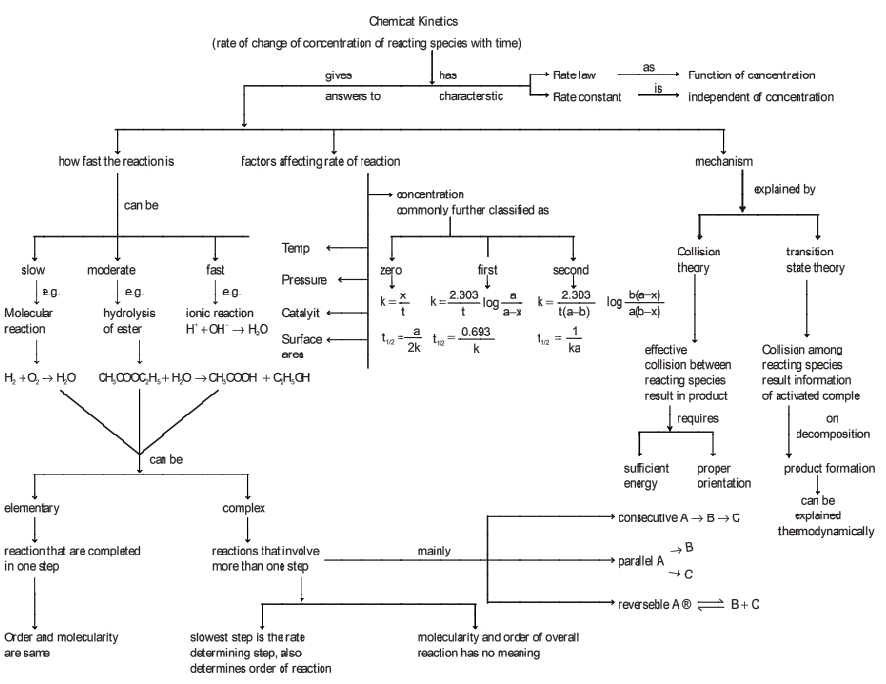
UNIT - 4 Chemical Kinetics
The feasibility of any chemical reaction can be predicted thermodynamically but this study cannot give answer to
-
how fast the reaction would be
-
what parameters can change the rate of reaction
-
what mechanism does it follow to form products
Thus, the branch of physical chemistry that deals with the study of rate of the reaction and the factors such as temperature; pressure, concentration, light that govern the rate and the mechanism by which the reaction proceeds is called Chemical Kinetics
Based on the time taken by the reaction for its completion, various reactions are divided into three categories:
The reactions can be classified as fast, slow or moderate reactions.
- Fast reaction : These reactions are so fast that they occur as soon as the reactants are brought together. Generally, such reactions involve ionic species.
- Slow reaction : These reactions may take months/years for their completion.
Carbon and oxygen are thermodynamically less stable than
- Moderate reaction : Between these two extremes there are many reactions which occur at measurable speed and are commonly studied under chemical kinetics.
Factors Influencing the Rates of Reaction
-
Nature of the Reactants: The nature of the reactants play an important role in influencing the rate of a reaction For eg: Both ferrous ions and oxalate ions can be oxidised by acidified
-
Concentration of the Reactants: As a reaction proceeds, the reactants are consumed. Greater the concentration, faster is the reaction.
-
Temperature of the system: Generally, rate of reaction almost becomes double for every
-
Presence of catalyst: It increases the speed of reaction by lowering the activation energy barrier i.e., a new path is followed with lower activation energy. However, Presence of a catalyst cannot make a non-spontaneous reaction feasible.
-
Surface area of the reactants: Greater the surface area, faster is the reaction. That is why pulverised wood or powdered coal burns faster than log of wood or a lump of coal (reactions involving solid reactants)
-
Presence of light: It provides the necessary activation energy and the reaction starts (photochemical reactions).
Effect of change of Pressure or volume of the Vessel on the Rate of Reaction
If volume of the Vessel is doubled, concentrations are halved. Then, new rate is given as
If volume of vessel is reduced to
If at constant temperature, pressure is doubled, volume is reduced to half. Hence, concentrations are doubled. Then, new rate is given as:
Rate Law and order of a Reaction
- Rate of a reaction: It is defined as the change in concentration of the reactant or product per unit time.
The change in concentration with time is graphically represented as shows in Fig (1 and 2):
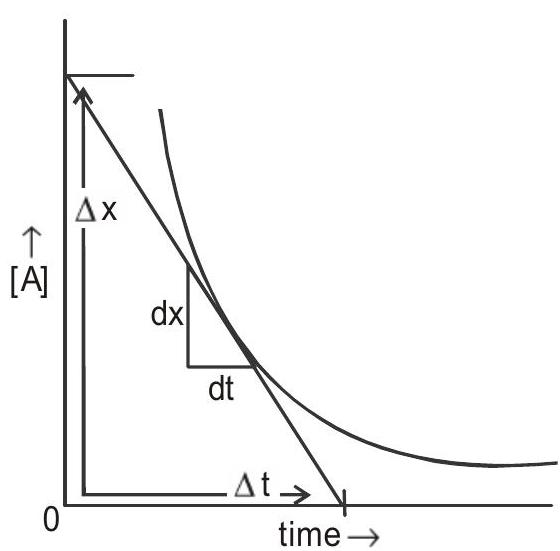
Fig 1: Plot of change in concentration of a reactant with time
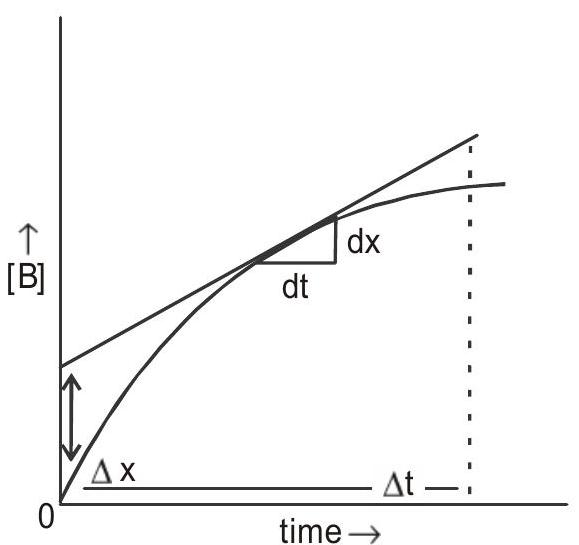
Fig 2: Plot of change in concentration of product with time
Rate of a reaction is defined in two ways
- Average rate :- Change in concentration of a reactant or a product over time interval
- Instantaneous rate : It is calculated from
Note:
For the reaction,
- Rate law : Rate law is the expression in which reaction rate is given in terms of molar concentration of reactants with each term raised to some power (which is determined experimentally) which may or may not be equal to their stoichiometric coefficient.
For a reaction,
where
Difference between rate of reaction and rate constant:
| Rate of reaction | Rate constant | |
|---|---|---|
| i) | It is a speed with which reactants are converted into product; or products are formed. | It is a proportionality constant. |
| ii) | It is a function of initial concentration of reactants | It is independent of the initial concentration of reactant(s). |
| iii) | It is measured as the rate of decrease of concentration of reactants or rate of increase of concentration of products. Each term divided by its stoichiometric cofficient. | It is equal to the rate of reaction when concentration of each reactant is unity. |
| iv) | It’s unit is |
Its unit depends upon the order of reaction. In general, unit of rate constant is |
Measurement of the Rate of reaction:
In order to measure the rate of a reaction, the progress of reaction is followed by monitoring the concentration of one of the reactant or product at different intervals of time.
There are various methods of following the same for eg. in gaseous reaction the rate of the reaction can be calculated either by collecting volumes of one of gas or by measuring change in pressure of a gas at different intervals of time.
In liquid phase, the reactions can be investigated by monitoring different physical parameters for eg. change in refractive index, change in angle of plane polarised light, change in conductance at different intervals of time. For investigating moderate reactions (neither fast nor slow) the most commonly used technique is volumetric analysis. In this method a small amount of reaction mixture
Based on the dependence of the reaction on the concentration of reacting species, various reactions can be classified as:
Reaction of Zero Order: When the rate of reaction is independent of the concentration of all the reactants.
- Consider a general reaction,
If it is of zero order, then
On Integration, we get
At
or
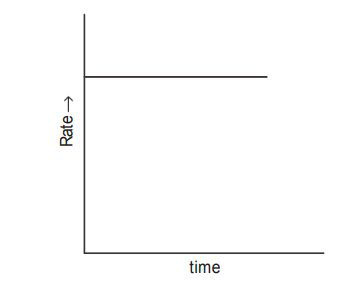
Fig 3: Variation of rate of reaction with time for zero order reaction
Zero order reaction will proceed with a constant rate and the rate will drop to zero at the end of reaction.
Examples of Zero Order Reactions
(i) Photochemical reactions: These reactions occur in the presence of light. Many such reactions are found to be of Zero order. For e.g., the combination between hydrogen and chlorine in the presence of light may be studied by enclosing these gases in a tube and inverting the tube in a trough of water.
(ii) Heterogeneous reactions: A reaction in which the reactants, product and catalyst are present in different phases. The decomposition of
Expression for Half change period
Half-change period is the time taken for half of the reaction to complete, i.e., the time in which half of the reactant is consumed in a reaction.
When
i.e.,
Thus,
When reaction is complete,
Comparision between
Reactions of First Order: A reaction is said to be of first order if rate of the reaction depends upon one concentration term only. For the reaction
Rate of reaction
For the reaction,
Rate of reaction
For the reaction,
Rate of reaction
Consider the simplest case viz
Rate
Intergrating both sides
when
Substituting the value of ’
or
where
If the initial concentration of reactant is ’
or
The exponential form of the expression for first order reaction is
Modified expression for first order rate equation
- Reaction in gaseous phase
Initial
After time
Total pressure after time
or
Pressure of
Now,
Hence,
-
Some Important Characteristics of First Order Reactions
-
Rate constant of a first order reaction can be also be calculated by measuring the concentration of the reactant at two different time when the initial concentration is not known.
Let
Subtracting equation (i) from (ii) we get:
- Half change period of a first order reaction is independent of the intial concentration of the reactant
Also, for first order reaction
Examples of the Reaction of First Order
-
Reactions taking place in the gaseous phase- e.g. decomposition of
-
Reactions taking place in the solution- e.g. conversion of
-
The Radioactive decay follows first order kinetics
Pseudo first order reaction
These are those reactions with higher order but under certain conditions become reactions of the first order
Consider a reaction
Expected rate law
When either of the reactant is taken in excess, say
The examples are :-
1) Acid catalysed hydrolysis of ester
Here, water is taken in excess and therefore its concentration may be taken as constant. Hence,
The reaction is therefore pseudo first order. The rate constant for this reaction is given as:
where
2). Inversion of cane sugar :- This is also an example of pseudo first order reaction, water being present in excess
The rate is measured by measuring the change in the angle of rotation by polarimeter. The change produced in the angle of rotation in time ’
Reactions of
Half-change Period and Fractional Change Time
General Expression for
For zero order reactions,
For 1 st order reactions,
For 2nd order reactions,
In general, for reaction of
Time for
For
For reactions of first order,
Expression for the amount left after
After one half-life, amount left
After two half-lives, amount left
After three half-lives, amount left
In general, amount left after
No. of half lives
Determination of order of reaction from half life measurement: If
Molecularity:
The number of atoms, ions or molecules that must collide with one another simultaneously so as to result into a chemical reaction is called the molecularity of the reaction. Reactions generally have molecularity of 1,2 or 3 . Reactions with molecularity more than 3 are very rare because chances for larger number of molecules to come simulaneously for collision are less.
The reactions are either elementary or complex in nature.
Elementary reactions- The reactions taking place in one step are called elementary reactions.
Complex reaction - The reactions which do not take place in one step but take place in a number of steps are called complex reactions. Each step of the complex reaction is an elementary reaction.
In complex reactions, the overall rate of the reaction is controlled by the slowest step in a reaction. It is also called as rate determining step.
- Mechanism of reactions- A series of steps proposed to account for the overall reaction is called the mechanism of reaction.
i) For the reaction,
experimentally, it is found that
This shows that the slowest step involves only one molecule of
hence, the probable mechanism is
ii) For reaction,
The order of reaction is two, Hence, the probable mechanism is
CHEMICAL KINETICS
Difference between order and molecularity of reaction
| Order of reaction | Molecularity | |
|---|---|---|
| i) | It is the sum of powers to which concentration terms are raised in final rate equation. | It is the number of atoms molecules or ions that are colloiding with each other in a single step. |
| ii) | it is an experimentally determined quantity | It is determined theoretically from balanced chemical equation. |
| iii) | Order of reaction always refers to overall reaction. | Molecularity of overall reaction has no meaning. It always refers to the species participating in a single step. |
| iv) | Knowledge of order of reaction helps in predicting the rate law of a reaction. | Knowledge of molecularity helps in predicting the mechanism of reaction. |
| v) | it is whole number, fractional or may be zero. The order of reaction w.r.t a species in reaction may be negative but overall order of reaction is always positive. | It is always a whole number. |
| vi) | order of reactions can be changed by changing physical parameters such as concentration, temperature. | Molecularity is always characteristic for each step and thus cannot be changed. |
Theories of Reaction Rates: The two well known theories to explain the rates of different reactions are:
(1) Collision theory
(2) Transition state theory or Theory of Absolute reaction rates
1) Collision theory
i) It is based upon the kinetic theory of gases according to which the molecules of a gas are continuously moving and hence colliding with each other.
ii) The number of collisions that takes place per second per unit volume of the reaction mixture is known as collision frequency (Z). The value of collision frequency is very high of the order of
iii) Every collision does not bring a chemical change. The collisions that actually produce the product are effective collisions. The effective collisions, which bring chemical change, are few in comparison to the total number of collisions. The collisions that do not form a product are ineffective elastic collisions, i.e., molecules just collide and disperse in different directions with different velocities.
iv) For a collision to be effective, the following two barriers are to be cleared,
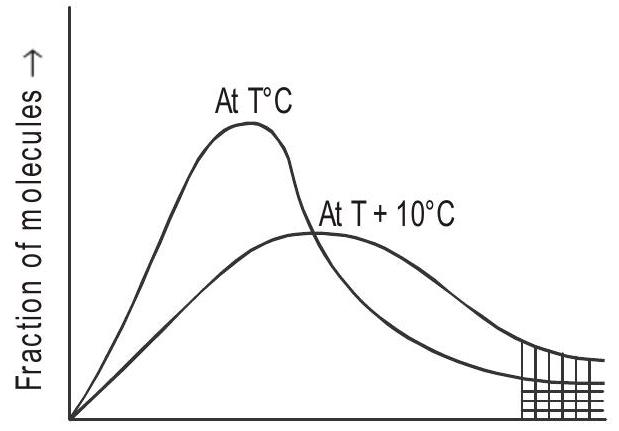
Fig 4: Energy of reactants
a) Energy barrier: “The minimum amount of energy which the colliding molecules must possess as to make the chemical reaction to occur, is known as threshold energy”.
-
In Fig. 4 ‘E’ corresponds to fraction of molecules capable of bringing effective collision.
-
There is an energy barrier for each reaction. The reacting species must be provided with sufficient energy to cross the energy barrier.
b) Orientation barrier: The colliding molecules should also have proper orientation so that the old bonds may break and new bonds are formed.
For example, 
Fig. 5: Role of orientation of molecules during collision
v) Thus, the main points of collision theory are as follows,
a) For a reaction to occur, there must be collisions between the reacting species.
b) Only a certain fraction of the total number of collisions is effective in forming the products.
c) For effective collisions, the molecules should possess sufficient energy as well as orientation.
vi) The fraction of effective collisions, under ordinary conditions may vary from nearly zero to about one for ordinary reactions. Thus, the rate of reaction is proportional to:
a) The number of collisions per unit volume per second (Collision freqeuncy, Z) between the reacting species
b) The fraction of effective collisions (Properly oriented and possessing sufficient energy). If
which is similar to Arrhenius equation, given as
on comparing these two equation
where the pre-exponential factor
- Logarithmic form of Arrhenius equation- Taking logarithm of both sides of Arrhenius equation, we get
If
Arrhenius equation can also be written in the form
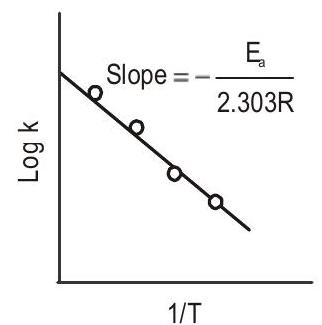
Fig 6: Plot of
- In the Arrhenius euqation,
the exponential factor is dimensionless
therefore, pre-exponential factor
- In the Arrhenius equation, when
Activation energy
The minimum extra amount of energy absorbed by the reactant molecules so that their energy becomes equal to threshold value is called activation energy . In other words, activation energy is the difference between the threshold energy and the average kinetic energy of the reactant molecules, i.e.,
Activation energy
Evidently, lesser is the activation energy, faster is the reaction or greater is the activation energy, slower is the reaction
The physical meaning of the activation energy is that it is the minimum relative kinetic energy which the reactant molecules must possess for changing into the products molecules during their collision. This means that the fraction of successful collision is equal to
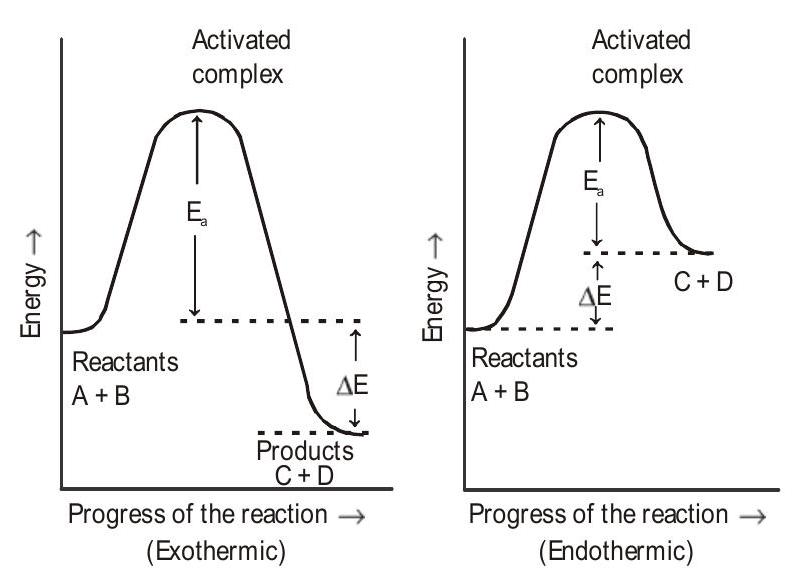
Fig. 7: Activation energy of exothermic and endothermic reactions
Limitations of Collision theory:-
(a) It is applicable to simple gaseous reactions only.
(b) It is supposed that only the kinetic energy of the colliding molecules contribute to the energy required for passing the energy barrier: There is no reason why rotational and vibrational energies of molecules should be ignored.
(c) The collision theory doesn’t talk about the manner in which old bonds are broken and new bonds are formed.
(d) There is no method for determining the number of molecules colliding with proper orientation.
Transition state theory: According to this theory, before the reacting molecules change into product, they form intermediates, called activated complex which has energy higher than both the reactants and products. The activated complex is supposed to be in equilibrium with reactant molecules i.e., it can either return to the initial reactants or proceed to form the products.
This can be represented as:
By using some fundamental properties of the reacting molecules, it was shown by Eyring that the rate constant (k) for any reaction irrespective of its order or molecularity is given by
Where
Also,
Greater is the value of free energy of activation for a reaction, the slower will be the reaction.
Advantage over collision theory
i) In collision theory, the factor ’
ii) The concept of formation of activated complex is more appropriate than assuming that the molecules collide and form products.
Solved Examples
Question 1. For the reaction
The rate of reaction
Show Answer
Solution-
Rate
Question 2.
Show Answer
Solution-
Active mass
Mass of
Molar mass of
Active mass
Mass of
Molar mass of
Active mass
Question 3. For a reaction
| Rate/(mol L-1 |
||
|---|---|---|
| i) |
0.004 | |
| ii) |
0.008 | |
| iii) |
0.008 |
Calculate the overall order of the reaction and rate constant
Show Answer
Solution-
Rate law for the reaction can be
From first and second observations
Dividing eq
Similarly from observations (i) and (iii)
Order of reaction
From observation (i)
Question 4. The decomposition of the following reaction follows first order kinetics
At the begining of the reaction, only
Show Answer
Solution-
Expression for first order rate constant is given as
Question 5. The vapour pressure of two miscible liquids ’
Show Answer
Solution-
Given
After
Mole fraction of ’
For a just order reaction
Question 6. A reaction occurs via two paths. the value of rate constants and activation energies for two paths are
Show Answer
Solution-
According to collision theory
For two paths of the given reaction
At temp
At temp,
(activation energy is independent of temperature)
similarly
On comparing eq (1) and eq (2)
Question 7. Consider a reaction
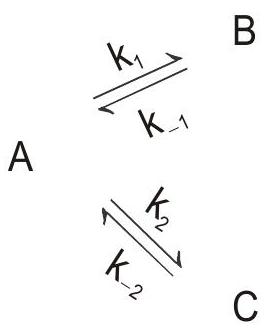
Show that concentration of ’
Show Answer
Solution-
Rate of the reaction is given as:
At equilibrium
PRACTICE QUESTIQNS
Question 1- During the kinetic study of the reaction
| S.No. | Initial rate of formation of |
||
|---|---|---|---|
| I | 0.1 | 0.1 | |
| II | 0.3 | 0.2 | |
| III | 0.3 | 0.4 | |
| IV | 0.4 | 0.1 |
Based on the above data which one of the following is correct?
(a) rate
(b) rate
(c) rate
(d) rate
Show Answer
Answer:- aQuestion 2- In the reaction
(a) The reaction is second order in
(b) The reaction is first order in NO
(c) The overall order of reaction is 2
(d) The overall order of reaction is 3
Show Answer
Answer:- cQuestion 3- Consider the reaction:
The rate equation for this reaction is rate
Which of these mechanisms is/are consistent with this rate equation?
A.
B.
(a) Neither A nor B
(b) A only
(c) B only
(d) Both
Show Answer
Answer:- bQuestion 4- The rate of a gaseous reaction is halved when the volume of the vessel is doubled. The order of reaction is
(a) 0
(b) 1
(c)
(d)
Show Answer
Answer:- bQuestion 5- For the reaction,
(a) 2
(b) 1
(c)
(d)
Show Answer
Answer:- cQuestion 6- The reaction
(a)
(b)
(c)
(d)
Show Answer
Answer:- cQuestion 7- Half-life of a reaction is found to be inversely proportional to the cube of initial concentration. The order of reaction is
(a) 4
(b) 3
(c) 5
(d) 2
Show Answer
Answer:- aQuestion 8- Consider the reaction,
(a)
(b)
(c) no unit
(d)
Show Answer
Answer:- bQuestion 9- For the reaction
(a) Second order
(b) Third order
(c) First order
(d) Zero order
Show Answer
Answer:- dQuestion 10- In the reaction,
the rate of appearance of bromine
(a)
(b)
(c)
(d)
Show Answer
Answer:- dQuestion 11-
the correct relation between
(a)
(b)
(c)
(d)
Show Answer
Answer:- bQuestion 12- The rate constant of nth order has units
(a) litre
(b)
(c)
(d)
Show Answer
Answer:- dQuestion 13- A hypothetical reaction
The order of the overall reaction is:
(a) 2
(b) 1
(c)
(d) 0
Show Answer
Answer:- cQuestion 14- For a first order reaction,
(a)
(b)
(c)
(d)
Show Answer
Answer:- aPRACTICE QUESTIONS
Question 1- The rate constants
(a)
(b)
(c)
(d)
Show Answer
Answer:- dQuestion 2- For a first order reaction
(a)
(b)
(c)
(d)
Show Answer
Answer:- dQuestion 3- For the first order gas phase decomposition reaction,
if
(a)
(b)
(c)
(d)
Show Answer
Answer:- dQuestion 4-
(a) 1.118
(b) 0.1118
(c) 18.11
(d) 11.18
Show Answer
Answer:- dQuestion 5- The following data is obtained during the first order thermal decomposition of
at constant volume and temperature
| S.No. | Time | Total pressure in pascals |
|---|---|---|
| 1 | At the end of 10 minutes | 300 |
| 2. | After completion | 200 |
The rate constant in
(a) 0.0693
(b) 6.93
(c) 0.00693
(d) 69.3
Show Answer
Answer:- aQuestion 6- The energies of activation for forward and reverse reactions for
(a) 20
(b) 300
(c) 120
(d) 280
Show Answer
Answer:- aQuestion 7- The rate constant of a reaction increases by 55 when its temperature is raised from
(a)
(b)
(c)
(d)
Show Answer
Answer:- aQuestion 8- The activation energy of a reaction is
(a)
(b)
(c)
(d)
Show Answer
Answer:- dQuestion 9- A chemical reaction was carried out at
(a)
(b)
(c)
(d)
Show Answer
Answer:- cQuestion 10- What is the time required for a first order reaction to be
(a) There is no change
(b) Time taken is double
(c) Time taken is triple
(d) Time required is half the initial value
Show Answer
Answer:- d