A solution is defined as a homogeneous mixture of two or more constituents (chemical species), whose composition can be varied within certain limits. These constituents cannot be separated by filtration, sedimentation or centrifugation. A binary solution has two constituents, ternary three, quaternary four. The solutions may be gaseous, liquid or solid. The physical state of a solution is the physical state of solvent. Generally, the constituent present in small quantity referred to as solute and the one present in large quantities is referred to as solvent.

The amount of solute dissolved in given amount of solvent/solution is referred to as the concentration of solute. This chapter focuses on solution obtained by dissolving solid/ liquid / gas as in a liquid.

In a given solution, let solute be represented by (1) and the solvent by (2)

$\mathrm{W} _{1}=$ mass of solute.

$m _{1}=$ molar mass of solute,

$\mathrm{n} _{1}=$ moles of solute.

$\mathrm{W} _{1}+\mathrm{W} _{2}=$ Mass of solution,

$\mathrm{d}=$ density in $\mathrm{g} \mathrm{cm}^{-3}$,

$E _{1}=$ equivalent mass of solute,

Methods of Expressing the Concentration of a solution

The concentration of a solution can be expressed in many ways. A few widely used terms are:

(a) Percent by volume (v/v) : The volume of solute in $\mathrm{mL}$ present in $100 \mathrm{ ~ mL}$ solution.

$ =\dfrac{\text { volume of solute }}{\text { volume of solution }} \times 100 $

(b) Percent mass by volume (w/v) : The mass of solute present in $100 \mathrm{ ~ mL}$ solution.

$ =\dfrac{\text { mass of solute }}{\text { volume of solution }} \times 100 $

(c) Strength : The amount of solute in grams present in $1000 \mathrm{ ~ mL}$ or IL solution.

$ =\dfrac{\text { mass of solute (in g) }}{\text { volume of solution (in } \mathrm{mL} \text { ) }} \times 1000 $

(d) Molarity (M) : The number of moles of solute per litre or per $\mathrm{dm}^{3}$ of the solution.

$ =\dfrac{\text { moles of solute }}{\text { volume of solution (in } \mathrm{L} \text { ) }} $

(e) Mole fraction $\left(X _{i}\right)$ : The ratio of number of moles of one component to the total number of moles of all the components present in the solution.

$ X _{1}=\dfrac{n _{1}}{n _{1}+n _{2}} ; X _{2}=\dfrac{n _{2}}{n _{1}+n _{2}} $

(f) Molality $(\mathrm{m})$ : The number of moles of solute present in $1 \mathrm{ ~ kg}$ of the solvent.

$ =\dfrac{\text { moles of solute }}{\text { mass of solvent (in } \mathrm{kg})}$

$ =\dfrac{1000 \mathrm{w} _{2}}{\mathrm{w} _{1} \mathrm{ ~ m} _{2}}$

(g) Normality (N) : The number of gram equivalents of solute present per litre of solution.

$=\dfrac{\text { gram equivalents of solute }}{\text { volume of soution (in } L \text { ) }}$

$=\dfrac{\mathrm{W} _{2} / \mathrm{E} _{2}}{\mathrm{ ~ V}}=\dfrac{\mathrm{W} _{2}}{\mathrm{VE} _{2}}$

(h) Formality (F) : The number of formula mass in gram present per litre of solution. In case, formula mass is equal to molecular mass, formality is equal to molarity.

(i) Parts per million ( $\mathrm{ppm})$ : When the solute is present in trace quantities, the concentration is often expressed in ppm. It is the amount of solute in ‘gram’ present in $10^{6} \mathrm{gram}$ of solution.

$=\dfrac{\text { mass of solute }}{\text { mass of solution }} \times 10^{6}$

Relation between various concentration terms

(i) Mole fraction and molality

$ \begin{gathered} X _{2}=\dfrac{n _{2}}{n _{1}+n _{2}} \quad X _{1}=\dfrac{n _{1}}{n _{1}+n _{2}} \\ \dfrac{X _{2}}{X _{1}}=\dfrac{n _{2}}{n _{1}}=\dfrac{w _{2} / m _{2}}{w _{1} / m _{1}}=\dfrac{w _{2} m _{1}}{w _{1} m _{2}} \\ \text { or } \dfrac{1000 X _{2}}{m _{1} X _{1}}=\dfrac{1000 w _{2}}{m _{2} w _{1}}=\text { molality }(m) \\ m=\dfrac{1000 X _{2}}{m _{1} X _{1}}=\dfrac{1000 X _{2}}{\left(1-X _{2}\right) m _{1}} \end{gathered} $

(ii) Molarity and mole fraction :

Mass of solution $=n _{1} m _{1}+n _{2} m _{2}$ volume of solution $=\dfrac{\text { mass }}{\text { density }}=\dfrac{\left(n _{1} m _{1}+n _{2} m _{2}\right)}{d}$

Molarity $=\dfrac{\text { moles of solute }}{\text { volume of solution }} \times 1000$

$ =\dfrac{1000 n _{2} d}{\left(n _{1} m _{1}+n _{2} m _{2}\right)} $

Dividing both numerator and denominator by $\left(n _{1}+n _{2}\right)$

$ \begin{gathered} M=\dfrac{1000 d\left(n _{2}\left(n _{1}+n _{2}\right) x\right.}{\left(\dfrac{n _{1}}{n _{1}+n _{2}} m _{1}+\dfrac{n _{2}}{n _{1}+n _{2}} m _{2}\right)}=\dfrac{X _{2} \times 1000 x d}{X _{1} m _{1}+X _{2} m _{2}} \\ M=\dfrac{1000 d X _{2}}{X _{1} m _{1}+X _{2} m _{2}} \end{gathered} $

(iii) Molarity of mixing : Let there be three samples of solution (containing same solvent and solute) with their molarity $M _{1}, M _{2}, M _{3}$ and volumes $V _{1}, V _{2}, V _{3}$ respectively. These solutions are mixed, molarity of mixed solution may be given as: $\mathrm{M} _{1} \mathrm{ ~ V} _{1}+\mathrm{M} _{2} \mathrm{ ~ V} _{2}+\mathrm{M} _{3} \mathrm{ ~ V} _{3}=\mathrm{M}\left(\mathrm{V} _{1}+\mathrm{V} _{2}+\mathrm{V} _{3}\right)$

where, $\mathrm{M}=$ resultant molarity

$V _{1}+V _{2}+V _{3}=$ resultant volume after mixing

(iv) Molarity (M) and Molality (m)

Molarity means M moles of solute in $1 \mathrm{ ~ L}$ of solution.

mass of solute $=m _{1} M$

mass of solution $=(1000 \times d)$

$\Rightarrow$ mass of solvent $=1000 \mathrm{ ~ d}-\mathrm{m} _{1} \mathrm{M}$

Molality $(m)=\left(\dfrac{1000 M}{1000 d-m _{1} M}\right)$

Note :

(a) Molality is the most convenient method to express concentration and is independent of temperature.

(b) Molarity is dependent on volume and hence on temperature as well.

(c) A millimolar solution is $0.001 \mathrm{M}$.

(d) Molarity can also be expressed in terms of density (d) of solution.

$\mathrm{d}=$ density of solution $(\mathrm{g} / \mathrm{mL})$

Let it contains $x \%$ solute by mass

$\Rightarrow$ mass of 1 litre solution $=1000 \mathrm{ ~ d}$

mass of solute in $1 \mathrm{ ~ L}$ solution $=\dfrac{1000 \mathrm{xd}}{100}$

Molarity $=$ number of moles of solute in $1 \mathrm{ ~ L}$

$M=\dfrac{10 x d}{m _{2}}$

Solved Examples:

Question 1. A solution is prepared by mixing equal volumes of solution $\mathrm{A}, 49 \%$ by mass of $\mathrm{H} _{2} \mathrm{SO} _{4}$ (density $=1.8 \mathrm{ ~ g} / \mathrm{mL}$ ) and solution $\mathrm{B}, 70 \%$ by mass of $\mathrm{H} _{2} \mathrm{SO} _{4}$ (density $=1.6 \mathrm{ ~ g} / \mathrm{mL}$ ). What is the molality and molarity of resulting solution?

For Calculating molarity of the resulting solution:

Let the mass of each solution taken be $100 \mathrm{ ~ g}$

Solution A

Volume of $100 \mathrm{ ~ g}$ of $49 \%$ by mass of $\mathrm{H} _{2} \mathrm{SO} _{4}$

$=\dfrac{100}{d}=\dfrac{100}{1.8} \mathrm{ ~ mL}$

$=\dfrac{100}{1.8 \times 1000} \mathrm{ ~ L}$

No. of moles of $\mathrm{H} _{2} \mathrm{SO} _{4}$ in $100 \mathrm{ ~ g}$ of solution

$=\dfrac{49}{98}$

Molarity of this solution ’ $A$ ’ $=\dfrac{49 \times 1.8 \times 10}{98 \times 1}$

$ =9 \mathrm{M} $

Solution B

Volume of $100 \mathrm{ ~ g}$ of $70 \%$ by mass of $\mathrm{H} _{2} \mathrm{SO} _{4}$

$=\dfrac{100}{1.6} \mathrm{ ~ mL}$

$=\dfrac{100}{1.6 \times 1000} \mathrm{ ~ L}$

No. of moles of $\mathrm{H} _{2} \mathrm{SO} _{4}$ in $100 \mathrm{ ~ g}$ of solution $\mathrm{B}$.

$=\dfrac{70}{98}$

Molarity of this solution $B$

$=\dfrac{70 \times 1.6 \times 10}{98 \times 1}=16.47 \mathrm{M}$.

Molarity of solution obtained by mixing equal volumes of solutions $A$ and $B$

Let $100 \mathrm{ ~ mL}$ of each solution be mixed

$M _{A} V _{A}+M _{B} V _{B}=M\left(V _{A}+V _{B}\right)$

$9 \times 100+16.47 \times 100=M \times 200$

$ M=12.74 \mathrm{M} $

The molarity of solution $=12.74 \mathrm{M}$

Question 2. A solution (density $1 \mathrm{ ~ g} \mathrm{ ~ mL}^{-1}$ ) is prepared by dissolving $2.65 \mathrm{ ~ g}$ of anhydrous sodium carbonate in $250 \mathrm{ ~ mL}$ solution. Calculate the following:

(i) mass percent of anhydrous sodium carbonate

(ii) mole fraction of anhydrous sodium carbonate

(iii) molalities of $\mathrm{Na}^{+}$and $\mathrm{CO} _{3}{ }^{2-}$ ions.

(iv) molarity of the solution

PRACTICE QUESTIONS

Question 1- A molal solution is one that contains one mole of solute in

(a) $1000 \mathrm{ ~ g}$ of solvent

(b) $1.0 \mathrm{ ~ L}$ of solvent

(c) $1.0 \mathrm{ ~ L}$ of solution

(d) $22.4 \mathrm{ ~ L}$ of solution

Question 2- In which mode of expression, the concentration of a solution remains independent of temperature?

(a) Molarity

(b) Normality

(c) Formality

(d) Molality

Question 3- Dissolving $120 \mathrm{ ~ g}$ of urea (mol. wt. 60) in $1000 \mathrm{ ~ g}$ of water gave a solution of density $1.15 \mathrm{ ~ g}$ $\mathrm{mL}^{-1}$. The molarity of the solution is

(a) $1.78 \mathrm{M}$

(b) $2.00 \mathrm{M}$

(c) $2.05 \mathrm{M}$

(d) $2.22 \mathrm{M}$

Question 4- The molarity of a solution obtained by mixing $750 \mathrm{ ~ mL}$ of $0.5 \mathrm{M} \mathrm{HCl}$ with $250 \mathrm{ ~ mL}$ of $2 \mathrm{M} \mathrm{HCl}$ will be

(a) $0.875 \mathrm{M}$

(b) $1.00 \mathrm{M}$

(c) $1.75 \mathrm{M}$

(d) $0.0975 \mathrm{M}$

Question 5- If equal volumes of $3.5 \mathrm{M} \mathrm{CaCl} _{2}$ and $3.0 \mathrm{M} \mathrm{NaCl}$ are mixed, what would be the molarity of chloride ion in the final solution?

(a) $2 \mathrm{M}$

(b) $3 \mathrm{M}$

(c) $4 \mathrm{M}$

(d) $5 \mathrm{M}$

Question 6- How many millilitres ( $\mathrm{mL}$ ) of $1 \mathrm{M} \mathrm{H} _{2} \mathrm{SO} _{4}$ solution is required to neutralise $10 \mathrm{ ~ mL}$ of $1 \mathrm{M}$ $\mathrm{NaOH}$ solution?

(a) $2.5 \mathrm{ ~ mL}$

(b) $5.0 \mathrm{ ~ mL}$

(c) $10.0 \mathrm{ ~ mL}$

(d) $20.0 \mathrm{ ~ mL}$

Question 7- The normality of $10 \%$ (weight/volume) acetic acid is

(a) $1 \mathrm{ ~ N}$

(b) $0.1 \mathrm{ ~ N}$

(c) $1.7 \mathrm{ ~ N}$

(d) $0.83 \mathrm{ ~ N}$

Question 8- Mole fraction of glucose in $18 \%$ (wt./wt.) solution of glucose is

(a) 0.18

(b) 0.1

(c) 0.017

(d) 0.021

Question 9- The molarity of pure water is

(a) 55.6

(b) 50

(c) 100

(d) 18

Question 10- A 5.2 molal aqueous solution of methyl alcohol $\left(\mathrm{CH} _{3} \mathrm{OH}\right)$ is supplied. What is the mole fraction of methyl alcohol in the solution?

(a) 0.190

(b) 0.086

(c) 0.050

(d) 0.100

TYPES OF SOLUTIONS

Out of various types of solutions, we shall focus on solutions obtained by dissolving

(i) gas in liquid

(ii) liquid in liquid

(iii) solid in liquid

Gas in liquid : A few examples are aerated drinks, natural water, house cleaner. Factors affecting the solubility of gas in liquid

(i) Nature of the gas and liquid

(ii) Temperature

(iii) Pressure

Dissolution of a gas in a liquid is an exothermic process therefore solubility of most of the gases in liquid decreases with increase of temperature, It is because of this, the Global warming is alarming for survival of aquatic life as it is decreasing the concentration of the dissolved oxygen in water. Pressure is the most important factor that influences the solubility of gas.

Effect of pressure on the solubility of a gas in a liquid (Henry’s law)

• Mass of a gas dissolved in a given volume of liquid at constant temperature is directly proportional to the pressure of the gas in equilibrium with the liquid.

$ \begin{aligned} & m \propto P \\ & m=K \cdot p \end{aligned} $

• For mixture of gases in equilibrium with a liquid, the partial pressure of each gas is directly proportional to the mole fraction of the gas in the solution.

$p _{A}=K _{H} X _{A} \quad-\quad$ (Unit of $K _{H}=$ atm or bar)

(a) $K _{\mathrm{H}}$ is a function of nature of the gas.

(b) Greater the value of $K _{\mathrm{H}}$, lower is the solubility at the same pressure.

(c) $K _{\mathrm{H}}$ increases with increase of temperature implying that solubility decreases with increase of temperature at the same pressure.

Applications of Henry’s Law

(i) In production of carbonated beverages. Under high pressure, solubility of $\mathrm{CO} _{2}$ increases. On opening the bottle to atmospheric pressure solubility decreases and the gas bubbles out.

(ii) In deep sea diving. Compressed air cylinder is used to get more oxygen in the blood but dissolved nitrogen causes a disease called decompression sickness. Hence, air diluted with helium is used.

(iii) In the function of lungs. In the lungs, partial pressure of $\mathrm{O} _{2}$ is high. It combines with haemoglobin to from oxyhaemoglobin. In the tissues, partial pressure of $\mathrm{O} _{2}$ is low. Therefore, $\mathrm{O} _{2}$ is released from oxyhaemoglobin for functions of the cell.

(iv) For climbers or people living at high altitude. Concentration of $\mathrm{O} _{2}$ in the blood and tissues is so low that they feel weak and are unable to think properly, a disease called anoxia.

Limitations

Henry’s law does not hold good if :

• Pressure is very High

• Temperature is very low

• Gas combines chemically with solvent

Exceptions

The solubility of $\mathrm{NH} _{3}$ or $\mathrm{CO} _{2}$ in water is high because of the following reaction :

$\mathrm{NH} _{3}+\mathrm{H} _{2} \mathrm{O} \rightleftharpoons \mathrm{NH} _{4} \mathrm{OH} \rightleftharpoons \mathrm{NH} _{4}{ }^{+}+\mathrm{OH}^{-}$

$\mathrm{CO} _{2}+\mathrm{H} _{2} \mathrm{O} \rightleftharpoons \mathrm{H} _{2} \mathrm{CO} _{3}$

Solubility of oxygen is blood is abnormally high because of the presence of haemoglobin in blood

$\mathrm{Hb}+4 \mathrm{O} _{2} \rightleftharpoons \mathrm{Hb}\left(\mathrm{O} _{2}\right) _{4}$

Vapour pressure of a solution

Let some pure liquid be taken in a closed vessel, The liquid at the surface vapourises and fills the available space. After sometime, an equilibrium is established between the liquid and vapour phases. The pressure exerted by the vapours in this state is referred to as the vapour pressure of liquid.

If some solute(solid/liquid) is added to this solvent two possibilities arise:

(i) solute is volatile

(ii) solute is non-volatite

(i) Solute is volatile

The solution is taken in a container and closed with a lid. The vapour phase contains vapour of both solute and solvent. The total pressure exerted by these vapours is referred to as the vapour pressure of solution. The partial vapour pressure of a component in such type of solution is given by Raoult’s Law.

(ii) Solute is non-votalile

There is no contribution from solute in the vapour phase. The vapour pressure of such solution is equal to the partial vapour pressure of solvent molecules

Raoult’s law for volatile liquids

In a solution the vapour pressure of a component at a given temperature is equal to the mole fraction of that component in the solution multiplied by the vapour pressure of that component in the pure state.

$ \begin{aligned} & p _{A}=p _{A}^{0} X _{A} \\ & p _{B}=p _{B}^{0} X _{B} \\ & p _{\text {total }}=p _{A}+p _{B}=X _{A} p _{A}^{0}+X _{B} p _{B}^{o} \\ & \quad=\left(1-X _{B}\right) p _{A}^{0}+X _{B} p _{B}^{O} \\ & \operatorname{or ~ } _{\text {total }}=\left(p _{B}^{O}-p _{A}^{O}\right) X _{B}+p _{A}^{O} \end{aligned} $

Hence, plot of $p _{\text {total }}$ vs $X _{B}$ should be a straight line. It is found to be so for ideal solution.

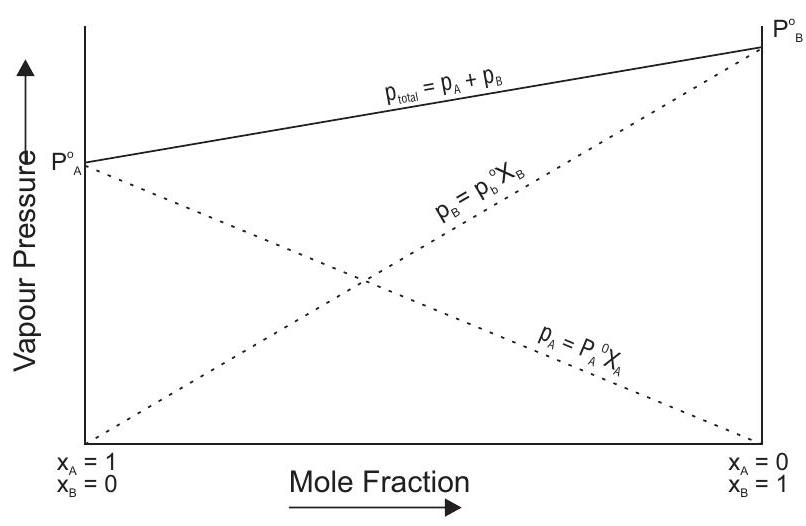
Formulation of ideal solution

Liquid pairs whose molecules are generally similar in size and structure form ideal solutions e.g. bromoethane and chloroethane

The mole fractions of the two constituents in the vapour phase are calculated as follows.

$ y _{A}=\dfrac{p _{A}}{p _{A}+p _{B}}=\dfrac{p _{A}}{p _{\text {total }}} $

$ \begin{aligned} y _{B} & =\dfrac{p _{B}}{p _{A}+p _{B}}=\dfrac{p _{B}}{p _{\text {total }}} \\ y _{B} & =1-y _{A} \end{aligned} $

• Raoult’s law is applicable only if the two components forming the solution have similar structure, e.g., benzene + toluene, hexane + heptane etc. Their solutions are called ideal solutions.

• The law is not applicable if the components are not completely miscible or if the components have widely different structures.

• Effect of adding non-volatile solute on vapour pressure of a liquid. The vapour pressure of a liquid decreases if some non-volatile solute is dissolved in it because some molecules of the solvent on the surface are replaced by the molecules of the solute.

• Vapour pressure of solutions of solids in liquid (Raoult’s law for non-volatile solutes)

As solute is non-volatile,

V.P. of solution $\left(p _{s}\right)=$ V.P. of solvent in solution

$=$ Mole fraction of solvent in solution $x$ V.P. of pure solvent

$p=p^{\circ} X _{A}$

$\dfrac{p}{p^{0}}=X _{A}=\dfrac{n _{A}}{n _{A}+n _{B}}$

$\therefore \quad 1-\dfrac{\mathrm{P}}{\mathrm{P}^{0}}=1-\mathrm{X} _{\mathrm{A}}$

or $\quad \dfrac{p^{0}-p}{p^{0}}=X _{B}$

This is Raoult’s law for non volatile solute

$ \dfrac{p^{o}-p}{p^{o}}=\dfrac{\Delta p}{p^{0}} $

is known as relative lowering of vapour pressure.

Relative lowering of vapour pressure of a solution containing a non volatile solute is equal to the mole fraction of the solute in the solution.

For a dilute solution

$ \dfrac{\mathrm{p}^{0}-\mathrm{p} _{\mathrm{s}}}{\mathrm{p}^{0}}=\dfrac{n _{B}}{n _{A}}=\dfrac{W _{B}}{M _{B}} \times \dfrac{M _{A}}{W _{A}} $

Ideal Solutions

A solution in which each component obeys Raoult’s law under all conditions of temperatures and concentrations. In such solutions, the molecules of the liquid pair one generally similar in size and structure. Also, in such solutions :

(a) $\Delta \mathrm{H} _{\text {mix }}=0$

(b) $\Delta \mathrm{V} _{\text {mix }}=0$

(c) Forces between A-B are same as between A-A and B-B.

eg. Benzene + toluene, hexane + heptane, bromoethane + chloroethane

Vapour pressure diagram for ideal solutions is shown below

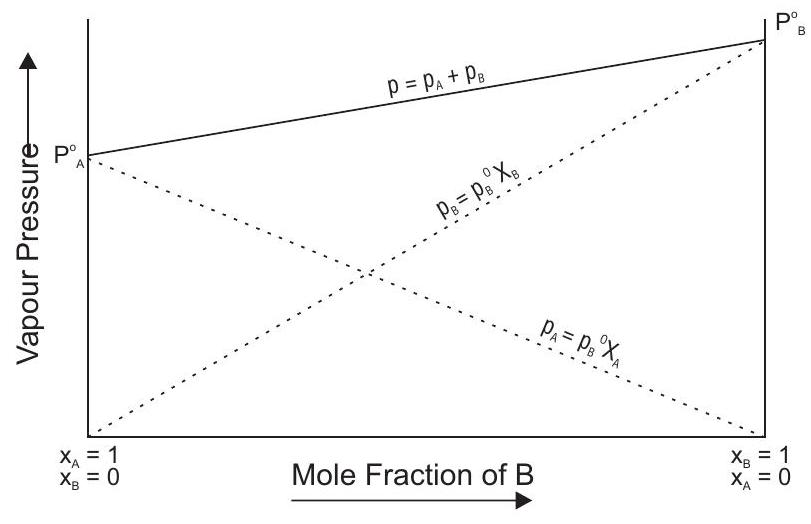
Formulation of non-ideal solution

Such solutions show either higher experimental values of vapour pressure ( $\mathrm{p} _{\text {total }}$ ) or lower experimental values of vapour pressure than those calculated from Raoult’s law. The cause for these deviations lies in the nature of interactions at the molecular level. On mixing two dissimilar substances, their molecular environment will change.

Non ideal solution

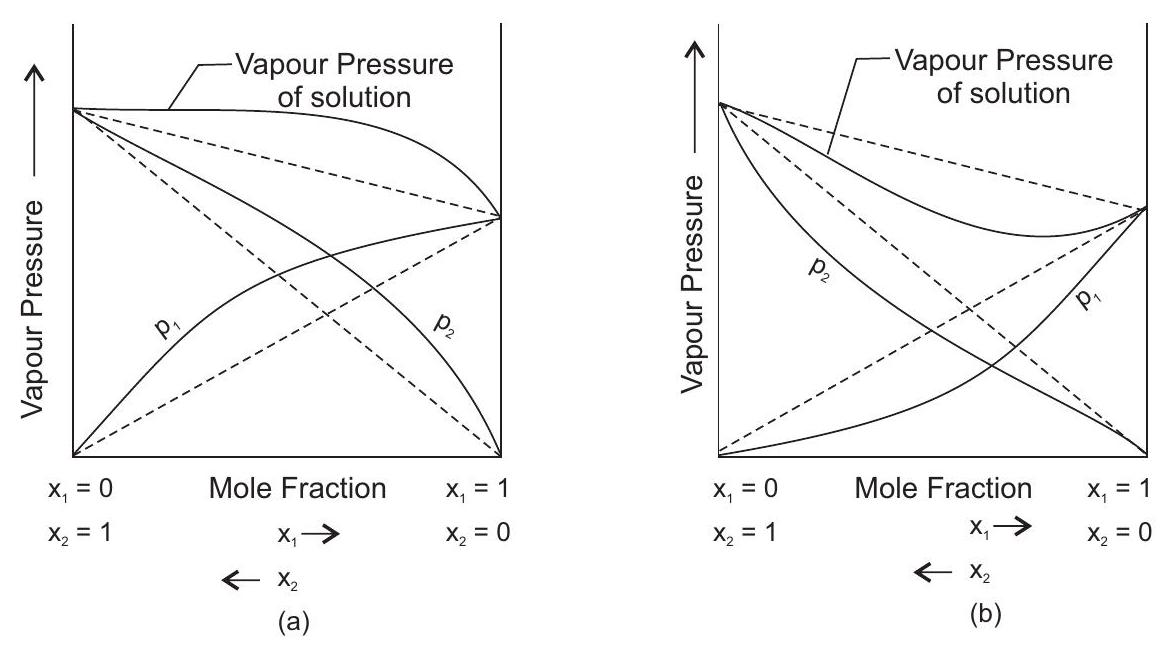
Raoult’s law is not valid when solute undergoes association or dissociation in given solvent.

Azeotropes

Liquid mixture, having the same composition, in liquid and vapour phase and boiling like a pure liquid is called a constant boiling mixture or an azeotropic mixture or an azeotrope.

Maximum Boiling Azeotropes

Solutions showing negative deviation from Raoult’s law and for which vapour pressure is minimum. The boiling point is more than either of the two components. For example, a mixture of nitric acid (b.pt. $359 \mathrm{ ~ K}$ ) and water (b. pt. $373 \mathrm{ ~ K}$ ) containing $68 \%$ nitric acid forms an azeotrope with b.pt. $393.15 \mathrm{ ~ K}$.

Minimum Boiling Azeotropes

Solutions showing positive deviation from Raoult’s law and for which vapour pressure is maximum. The boiling point is less than either of the two pure components. For example, mixture of ethanol (b. pt. $351.3 \mathrm{ ~ K}$ ) and water (b.pt. $373 \mathrm{ ~ K}$ ) containing $95.4 \%$ ethanol forms azeotrope with b.pt. $351.15 \mathrm{ ~ K}$.

Vapour pressure of liquid and temperature

Vapour pressure of liquid increases with temperature.

If vapour pressure of a liquid is known at a temperature, it can be calculated at another temperature using Clausius - Clapeyron equation

$ \log _{10}\left(\dfrac{p _{2}}{p _{1}}\right)=\dfrac{\Delta H _{v a p}}{2.303 R}\left(\dfrac{1}{T _{1}}-\dfrac{1}{T _{2}}\right) $

Colligative Properties

Properties which depend on the number of particles of solute and do not depend on the nature of solute. There are four colligative properties :

i) Relative lowering of vapour pressure

ii) Elevation in boiling point

iii) Depression in freezing point

iv) Osmotic pressure

RELATIVE LOWERING OF VAPOUR PRESSURE

Formula used (Raoult’s law for non-volatile solutes) for solid (non-volatile) solute dissolved in liquid,

$ \begin{aligned} & \dfrac{p^{0}-p}{p^{0}}=\dfrac{n _{B}}{n _{A}+n _{B}}=\dfrac{W _{B} / M _{B}}{W _{A} / M _{A}+W _{B} / \mathrm{M} _{B}} \\ = & \dfrac{n _{B}}{n _{A}}=\dfrac{w _{B} / M _{B}}{W _{A} / M _{A}} \text { for dilute solutions } \end{aligned} $

Since relative lowering of vapour pressure depends on the number of moles, so it is a colligative property.

ELEVATION IN BOILING POINT

Boiling point of a liquid is the temperature at which vapour pressure of liquid becomes equal to atmospheric pressure. As the vapour pressure of solution is lower than that of solvent, its boiling point is higher.

$\Delta T _{b}=K _{b} \cdot m$

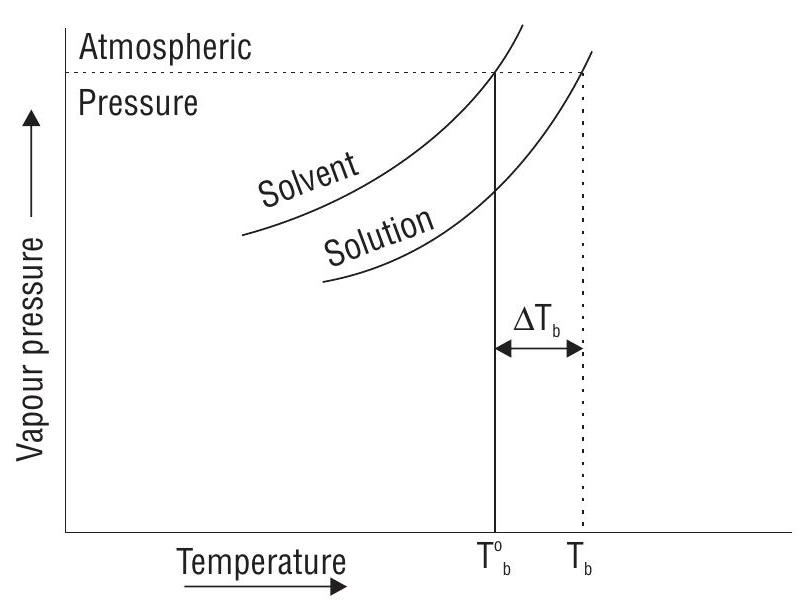
If $\quad m=1, \Delta T _{b}=K _{b}$

$K _{b}=$ Molal elevation constant / ebullioscopic constant

Ebullioscopic Constant

It is the elevation in boiling point when the molality of solution is unity.

SI unit : $\mathrm{K ~ kg} \mathrm{ ~ mol}^{-1}$

$\Delta T _{\mathrm{b}}=K _{\mathrm{b}} . m$

$T _{\mathrm{b}}-T _{\mathrm{b}}^{0}=K _{\mathrm{b}} \times \dfrac{\mathrm{W} _{\mathrm{B}}}{\mathrm{M} _{\mathrm{B}}} \times \dfrac{1000}{\mathrm{ ~ W} _{\mathrm{A}}}$

$T _{\mathrm{b}}=$ boiling point of solution

$T _{b}^{0}=$ boiling point of pure solvent

$W _{\mathrm{A}}=$ given mass of solvent

$W _{\mathrm{B}}=$ given mass of solute

$M _{\mathrm{B}}=$ molecular mass of solute

Relationship between $K _{b}$ and enthalpy of vaporisation $\left(\Delta _{\mathrm{vap}} \mathrm{H}\right)$

$ K _{\mathrm{b}}=\dfrac{M _{\mathrm{A}} R\left(T _{\mathrm{B}}^{\mathrm{b}}\right)^{2}}{1000 \times \Delta _{\text {vap }} H} $

Relationship between $\mathrm{K} _{\mathrm{b}}$ and latent heat of vaporisation $\left(\mathrm{I} _{\mathrm{v}}\right)$

$ K _{\mathrm{b}}=\dfrac{R\left(T _{\mathrm{B}}\right)^{2}}{1000 I _{\mathrm{V}}} $

DEPRESSION IN FREEZING POINT

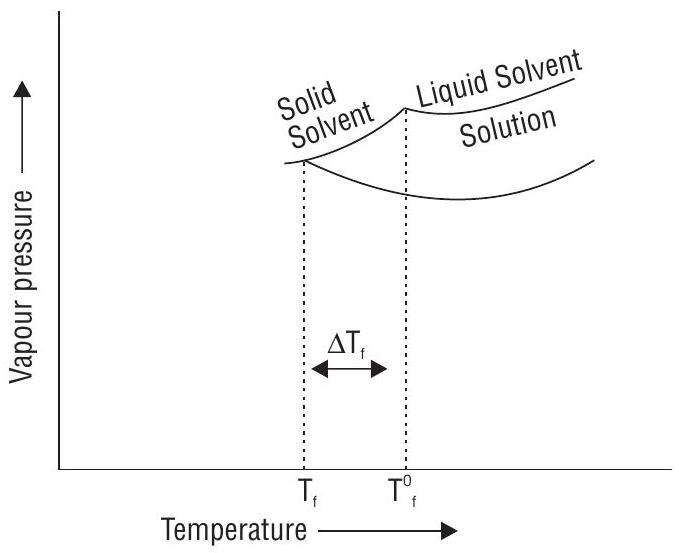
Freezing point of a substance is the temperature at which the solid and liquid forms of the substance are in equilibrium and their vapour pressures are equal. Freezing point of solution is always lower than that of the pure solvent.

Due to lower vapour pressure of the solution, solid from a solution separates out at lower temperature. The decrease is called the depression in freezing point.

$\Delta T _{\mathrm{f}}=T _{\mathrm{f}}^{0}-T _{\mathrm{f}}$

$T _{\mathrm{f}}^{0}=$ freezing point of pure solvent

$T _{\mathrm{f}}=$ freezing point of solution

Depression in freezing point is given by equation :

$\Delta T _{\mathrm{f}}=K _{\mathrm{f}} \cdot \mathrm{m}$

$\mathrm{K} _{\mathrm{f}}=$ molal depression contant / cryoscopic constant

If

$\mathrm{m}=1, \Delta T _{\mathrm{f}}=K _{\mathrm{f}}$

Molal Depression Constant

Depression in freezing point when molality of solution is unity. SI unit $=\mathrm{K} \mathrm{kg} \mathrm{mol}^{-1}$

Relationship between molal depression constant and enthalpy of fusion

$ K _{\mathrm{f}}=\dfrac{M _{\mathrm{A}} R\left(T _{\mathrm{f}}^{0}\right)^{2}}{1000 \Delta _{\mathrm{fus}} H} $

Relationship between molal depression constant and latent heat of fusion

$K _{\mathrm{f}}=\dfrac{R\left(T _{\mathrm{f}}\right)^{2}}{1000 I _{\mathrm{f}}}$

Applications of depression in freezing point

1. Ethylene glycol is used as antifreeze (causes depression in freezing point) in automobiles.

2. $\mathrm{NaCl}$ or $\mathrm{CaCl} _{2}$ is sprinkled on roads to melt ice because salt-ice mixture has very low freezing point.

OSMOSIS

Net spontaneous flow of solvent molecules from solvent to the solution or from less concentrated solution to a more concentrated solution through semipermeable menbrane.

Osmotic Pressure - Minimum excess pressure that must be applied on the solution to prevent the entry of solvent into the solution through the semipermeable membrance

Reverse 0smosis - If a pressure higher than osmotic pressure is applied on the solution the solvent will flow from the solution into the pure solvent through the semi permeable membrane. It is used in the desalination of sea water.

$ \begin{aligned} & \pi=c R T \\ & \\ & \pi=\dfrac{n _{\mathrm{B}}}{V} R T \\ & \\ & \pi=\dfrac{\mathrm{W} _{\mathrm{B}}}{\mathrm{M} _{\mathrm{B}}, \mathrm{V}} \mathrm{RT} \end{aligned} $

Isotonic solutions. Solution having the same osmotic pressure are called isotonic (or isosmotic) solutions: This is so only when they have the same molar concentration, $\left(\pi _{1}=\pi _{2}\right.$ when $\left.c _{1}=c _{2}\right)$, Thus, if a solution containing $w _{1} \mathrm{ ~ g}$ of solute 1 of molar mass $M _{1}$ in $V _{1}$ litre of the solution is isotonic with a solution containing $w _{2} g$ of solute 2 of molar mass $M _{2}$ in $V _{2}$ litre of the solution,

$\dfrac{\mathrm{W} _{1}}{\mathrm{M} _{1} \mathrm{ ~ V} _{1}}=\dfrac{\mathrm{W} _{2}}{\mathrm{M} _{2} \mathrm{ ~ V} _{2}}$

Knowing $M _{1}, M _{2}$ can be calculated.

• Hypotonic and hypertonic solutions : A solution having lesser osmotic pressure (lower concentration) than the other is called hypotonic. A solution having higher osmotic pressure (higher concentration) than the other is called hypertonic.

  • Example: A $0.91 \%$ solution of pure $\mathrm{NaCl}$ is Isotonic with human red blood corpuscles (RBC). A NaCl solution with concentration $<0.91 \%$ is called hypotonic and RBC will swell and even burst in this solution. A NaCl solution with concentration $>0.91 \%$ is called hypertonic. RBC shrink in this solution.

• Advantage of osmotic pressure method for polymers. Osmotic pressure method is the best method for determination of molar masses of polymers because for polymer solutions, observed value of any other colligative property is too low to be measured accurately. Moreover, it can be carried out at room temperature. No heating or cooling is required. Some polymers, e.g., proteins undergo a change on heating.

ASSOCIATION OR DISSOCIATION OF SOLUTE AND ABNORMAL MOLAR MASSES

• Abnormal molar mass. When the molar mass of a substance as determined by using colligative properties, does not come out to be same as expected theoretically, it is said to show abnormal molar mass.

• Abnormal molar mass is obtained when the substance in the solution undergoes dissociation, i.e., case of electrolytes (e.g., NaCl in water) or association (e.g., organic acids in benzene). Dissociation results in the increase in the number of particles and hence increase in the magnitude of colligative property and decrease in the molar mass (as in each formula, molar mass is inversely proportional to colligative property, e.g., $\mathrm{M} _{\mathrm{B}} \propto \dfrac{1}{\Delta \mathrm{T} _{\mathrm{b}}}$ or $\dfrac{1}{\Delta \mathrm{T} _{\mathrm{f}}}$ ). Association results in the reverse.

• Van’t Hoff factor. This factor was introduced to calculate the extent of association or dissociation

It is the ratio of the experimental value of the colligative property to the calculated value of the colligative property. It is represented by ’ $l$ ‘, i.e.,

$ \mathrm{i}=\dfrac{\text { Experimental value of the colligative property }}{\text { Calculated value of the colligative property }} $

As molar mass $\propto \dfrac{1}{\text{Colligative property}}$

hence, $I=\dfrac{\text { Calculated molar mass }}{\text { Observed molar mass }}=\dfrac{M _{\mathrm{c}}}{M _{0}}$

$I=\dfrac{\text { number of solute particles after association or dissociattion }}{\text { number of solute particles before association or dissociation }}$

Modified formulae for substances under going dissociation or association in the solution

$\pi=\mathrm{i} \dfrac{\mathrm{n}}{\mathrm{V}} R T$

$\dfrac{p^{0}-p}{p^{0}}=i X _{B}$

$\Delta T _{\mathrm{b}}=\mathrm{i} K _{\mathrm{b}} \mathrm{m}$

$\Delta T _{\mathrm{f}}=\mathrm{i} K _{\mathrm{f}} \mathrm{m}$

• Calculation of degree of dissociation. If one molecule of a substance $A$ dissociates to form $n$ particles, (molecules or ions) and $\alpha$ is the degree of dissociation, then starting with one mole of $A$.

$ \begin{array}{cccc} & \mathrm{A} & \rightarrow & \mathrm{nP} \\ \text{Initial} & 1 \mathrm{mol} & & 0 \\ \text{At eqm.} & 1-\alpha & & n \alpha \\ \end{array} $

Total no. of moles at equilibrium

$=1-\alpha+n \alpha$

$i=\dfrac{1-\alpha+n \alpha}{1}$

or

$\alpha=\dfrac{i-1}{n-1}$

e.g., in case of $\mathrm{BaCl} _{2}$,

$\mathrm{BaCl} _{2} \longrightarrow \mathrm{Ba}^{2+}+2 \mathrm{Cl}^{-}, \mathrm{n}=3$

• Calculation of degree of association. If $n$ molecules of a substance $A$ associate to from $A _{n}$ and $\alpha$ is the degree of association, then starting with one mole of $A$.

$ \begin{array}{cccc} & \mathrm{nA} & \longrightarrow & \mathrm{A}_{n} \\ \text{Initial} & 1 , \mathrm{mol} & & 0 \\ \text{At eqm.} & 1-\alpha & & \dfrac{\alpha}{\mathrm{n}} \\ \end{array} $

Total no. of moles at equilibrium

$=1-\alpha+\dfrac{\alpha}{n}$

$i=1-\alpha+\dfrac{\alpha}{n}$

or $\alpha=\dfrac{1-i}{\mid-i / n}$

e.g., in case of benzoic acid in benzene

$2 \mathrm{C} _{6} \mathrm{H} _{5} \mathrm{COOH} \longrightarrow\left(\mathrm{C} _{6} \mathrm{H} _{5} \mathrm{COOH}\right) _{2}, \mathrm{n}=2$

$\alpha$ is sometimes called apparent degree of dissociation or association.

Comparison of Osmotic Pressure, Freezing point, Boiling point of solutions of non electrolytes and Different Electrolytes

For comparison, the value of a colligative property or molar concentrations of particles (ions or molecules) are considered. Thus,

• As electrolytes dissociate to give ions. Solution of an electrolyte will show greater value of a colligative property than that of a non-electrolyte of same molar concentration.

• For solutions of different electrolytes ( $\mathrm{NaCl}, \mathrm{BaCl} _{2}$ etc.) of the same molar concentration, greater the number of ions produced, greater is the value of colligative property.

• Solutions of different non-electrolytes (urea, glucose etc,) of the same molar concentration will show the same value of the colligative property.

• Comparing solutions of the same or different non-electrolytes, greater the molar concentration, greater is the value of the colligative property.

• In case of polymers, elevation in boiling point and depression in freezing point values are very small and difficult to be measured experimentally.

• Osmotic pressure of mixture of two solutions of same substance having different osmotic pressure $\pi _{1}$ and $\pi _{2}$ is given as

$\qquad \pi _{1} \mathrm{ ~ V} _{1}+\pi _{2} \mathrm{ ~ V} _{2}=\pi\left(\mathrm{V} _{1}+\mathrm{V} _{2}\right)$

• Osmotic pressure of mixture of two solutions when $\mathrm{n} _{1}$ and $\mathrm{n} _{2}$ moles of two different solutes present in $V _{1}$ and $V _{2}$ volumes of the same solvent, respectively are mixed

$ \begin{aligned} & \qquad \pi=\pi _{1}+\pi _{2} \\ & \\ & \qquad =\dfrac{n _{1} I _{1} R T}{\left(V _{1}+V _{2}\right)}+\dfrac{n _{2} I _{2} R T}{\left(V _{1}+V _{2}\right)} \\ & \\ & \qquad \pi=\dfrac{\left(n _{1} I _{1}+n _{2} I _{2}\right)}{\left(V _{1}+V _{2}\right)} R T \end{aligned} $

Solved Examples

Question 3. Calculate the molar mass of the solute, $2.175 \mathrm{ ~ g}$ of which when added to $39 \mathrm{ ~ g}$ of benzene, decrease the vapour pressure of the benzene by $40 \mathrm{ ~ mm} \mathrm{ ~ Hg}$.

(Vapour pressure of pure benzene $=640 \mathrm{ ~ mm} \mathrm{ ~ Hg}$ ).

Question 4. The vapour pressure of water at $37^{\circ} \mathrm{C}$ is $150 \mathrm{ ~ mm} \mathrm{ ~ Hg}$. An aqueous solution containing $28 \%$ by mass of a liquid $B\left(M _{B}=140 \mathrm{ ~ g} \mathrm{ ~ mol}^{-1}\right)$ has a vapour pressure of $160 \mathrm{ ~ mm} \mathrm{ ~ Hg}$, calculate

(i) vapour pressure of pure liquid $B$;

(ii) composition of two components in the vapour phase;

(iii) vapour pressure of a solution containing equal mass of the two liquids;

(iv) vapour pressure of a solution containing equal number of moles of the two liquids.

Question 5. Calculate osmotic pressure of blood at $298 \mathrm{ ~ K}$ given that blood freezes at $272.44 \mathrm{ ~ K}$ and a solution of $3 \mathrm{ ~ g}$ of urea in $250 \mathrm{ ~ g}$ water freezes at $272.63 \mathrm{ ~ K}$. Take freezing point of water as 273 K.

Question 6. (a) A $10 \%(\mathrm{w} / \mathrm{w})$ solution of cane sugar (mol wt. $=342$ ) is isotonic with a $1 \%$ solution of substance $X^{0}$. What is the molecular weight of $X$ ? (b) What mass of cane sugar must be dissolved in $2 \mathrm{ ~ kg}$ of $\mathrm{H} _ {2} \mathrm{O}$ to yield a solution that will freeze at $-5.58^{\circ} \mathrm{C}$ ? $\left(\mathrm{K} _{\text {twater }}=1.86^{\circ} \mathrm{C} / \mathrm{m}\right)$

Question 7. A compound $\mathrm{C} _{38} \mathrm{H} _{30}$, when dissolved in benzene, partially dissociates as represented below: $\mathrm{C} _{38} \mathrm{H} _{30} \quad \leftrightarrows 2 \mathrm{C} _{19} \mathrm{H} _{15}$

The freezing point of the solution is lowered by $0.7^{\circ} \mathrm{C}$ when $20 \mathrm{ ~ g}$ of this compound is dissolved in $300 \mathrm{ ~ g}$ of benzene. What percentage of $\mathrm{C} _{38} \mathrm{H} _{30}$ molecules have dissociated $\left(\mathrm{K} _{\mathrm{f}}=\right.$ 4.9) 1 mol of substance be taken and

Question 8. Arrange the following solutions in the order of increasing boiling point and freezing point, osmotic pressure.

(a) $1 \mathrm{ ~ m}$ Urea

(b) $1 \mathrm{ ~ m} \mathrm{NaCl}$

(c) $1 \mathrm{ ~ m} \mathrm{Na} _{2} \mathrm{CO} _{3}$

(d) $1 \mathrm{ ~ m} \mathrm{Na} _{3} \mathrm{PO} _{4}$

Question 9. What are the structures of benzoic acid when $12.2 \mathrm{ ~ g}$ of it is dissolved in $1 \mathrm{ ~ kg}$ of benzene $\left(\mathrm{K} _{\mathrm{b}}\right.$ $\left.=2.6 \mathrm{ ~ K} \mathrm{ ~ kg} \mathrm{ ~ mol}^{-1}\right)$ and $1 \mathrm{ ~ kg}^{2}$ of acetone $\left(\mathrm{K} _{\mathrm{b}}=1.7 \mathrm{ ~ K} \mathrm{ ~ kg} \mathrm{ ~ mol}^{-1}\right)$. The elevation in boiling points are $0.13^{\circ} \mathrm{C}$ and $0.26^{\circ} \mathrm{C}$, respectively.

PRACTICE QUESTIONS

Question 1- For an ideal solution with $p _{A}{ }^{0}>p _{B}{ }^{0}$ Which of the following is true?

a). $\left(X _{A}\right) _{\text {liquid }}=\left(X _{A}\right) _{\text {vapour }}$

b). $\left(X _{A}\right) _{\text {liquid }}>\left(X _{A}\right) _{\text {vapour }}$

c). $\left(X _{A}\right) _{\text {liquid }}<\left(X _{A}\right) _{\text {vapour }}$

d). There is no relationship between $\left(X _{A}\right) _{\text {liquid }}$ and $\left(X _{A}\right) _{\text {vapour }}$

Question 2- The millimoles of $\mathrm{N} _{2}$ gas that will dissolve in $1 \mathrm{ ~ L}$ of water of $298 \mathrm{ ~ K}$ when it is bubbled through water and has a partial pressure of 0.96 bar. $K _{H}=76.8 \mathrm{k}$ bar)

a) $0.59$

b) $0.69$

c) $0.79$

d) $0.89$

Question 3- If two substances $A$ and $B$ have $p _{A}{ }^{\circ}: p _{B}{ }^{\circ}=1: 2$ and have mole fraction in solution $1: 2$, then mole fraction of $A$ in vapour is

a) $0.33$

b) $0.25$

c) $0.52$

d) $0.2$

Question 4- The mass of solute (molar mass $60 \mathrm{ ~ g} \mathrm{ ~ mol}^{-1}$ ) that must be added to $180 \mathrm{ ~ g}$ of water so that the vapour pressure of water is lowered by $10 \%$ is

a) $30 \mathrm{ ~ g}$

b) $60 \mathrm{ ~ g}$

c) $24 \mathrm{ ~ g}$

d) $120 \mathrm{ ~ g}$

Question 5- A solution has 1:4 mole ratio of pentane to hexane. Vapour pressures of pure hydrocarbons at $20^{\circ} \mathrm{C}$ are $440 \mathrm{ ~ mm} \mathrm{ ~ Hg}$ for pentane and $120 \mathrm{ ~ mm} \mathrm{ ~ Hg}$ for hexane. Mole fraction of pentane in the vapour phase is

a) $0.2$

b) $0.478$

c) $0.549$

d) $0.786$

Question 6- The elevation in boiling point, when $13.44 \mathrm{ ~ g}$ of freshly prepared $\mathrm{CuCl} _{2}$ are added to one kilogram of water, is ( $K _{b}=0.52 \mathrm{ ~ kg} \mathrm{ ~ K} \mathrm{ ~ mol}^{-1}$, molar mass of $\mathrm{CuCl} _{2}=134.4 \mathrm{ ~ g} \mathrm{ ~ mol}^{-1}$ )

a) $0.05$

b) $0.1$

c) $0.16$

d) $0.21$

Question 7- The Henry’s law constant for the solubility of $N _{2}$ gas in water at $298 \mathrm{ ~ K}$ is $1.0 \times 10^{5}$ atm. The mole fraction of $\mathrm{N} _{2}$ in air is 0.8 . The number of moles of $\mathrm{N} _{2}$ from air dissolved in 10 moles of water at $298 \mathrm{ ~ K}$ and $5 \mathrm{ ~ atm}$ pressure is.

a) $4.0 \times 10^{-4}$

b) $4.0 \times 10^{-5}$

c) $5.0 \times 10^{-4}$

d) $4.0 \times 10^{-6}$

Question 8- For a dilute solution containing $2.5 \mathrm{ ~ g}$ of a non-volatile non-electrolyte solute in $100 \mathrm{ ~ g}$ of water, the elevation in boiling point at $1 \mathrm{ ~ atm}$ pressure is $2^{\circ} \mathrm{C}$. Assuming concentration of solute is much lower than the concentration of solvent, the vapour pressure $[\mathrm{mm}-\mathrm{ ~ Hg}]$ of the solution is $\left(\mathrm{K} _{\mathrm{b}}=0.76 \mathrm{ ~ K} \mathrm{ ~ kg} \mathrm{ ~ mol}^{-1}\right)$.

a) $724$

b) $740$

c) $736$

d) $718$

Question 9- An azeotropic solution of two liquids has boiling point lower than either of them when it

a) shows negative deviation from Raoult’s Law

b) shows no deviation from Raoult’s Law

c) shows positive deviation from Raoult’s Law

d) is saturated

Question 10- On mixing, heptane and octane form an ideal solution. At $373 \mathrm{ ~ K}$, the vapour pressures of the two liquid components (Heptane and Octane) are $105 \mathrm{kPa}$ and $45 \mathrm{kPa}$ respectively. Vapour pressure of the solution obtained by mixing $25.0 \mathrm{ ~ g}$ of heptane and $35.0 \mathrm{ ~ g}$ of octane will be (molar mass of heptane $=100 \mathrm{ ~ g} \mathrm{ ~ mol}^{-1}$ and of octane $=114 \mathrm{ ~ g} \mathrm{ ~ mol}^{-1}$ )

a) $96.2 \mathrm{kPa}$

b) $144.5 \mathrm{kPa}$

c) $72.0 \mathrm{kPa}$

d) $36.1 \mathrm{kPa}$

Question 11- An aqueous solution containing $1 \mathrm{ ~ g}$ of urea boils at $100.25{ }^{\circ} \mathrm{C}$. The aqueous solution containing $3 \mathrm{ ~ g}$ of glucose in the same volume will boil at

a) $100.75^{\circ} \mathrm{C}$

b) $100.5^{\circ} \mathrm{C}$

c) $100.0^{\circ} \mathrm{C}$

d) $100.25^{\circ} \mathrm{C}$

Question 12- An aqueous solution of glucose boils at $100.01^{\circ} \mathrm{C}$. The molal elevation constant of water is $0.5 \mathrm{ ~ K} \mathrm{ ~ kg} \mathrm{ ~ mol}^{-1}$. The number of glucose molecules in the solution containing $100 \mathrm{ ~ g}$ of water is

a) $0.02 \times 10^{21}$ molecules

b) $3.01 \times 10^{21}$ molecules

c) $1.50 \times 10^{21}$ molecules

d) $1.204 \times 10^{21}$ molecules

Question 13- The solubility of a gas in water at $300 \mathrm{ ~ K}$ under a pressure of 100 atmospheres is $4 \times 10^{-3} \mathrm{ ~ kg}$ $\mathrm{L}^{-1}$. Therefore, the mass of the gas dissolved in IL solution under pressure of 250 atmospheres at $300 \mathrm{ ~ K}$ is

a) $2.5 \times 10^{-3} \mathrm{ ~ kg}$

b) $2.0 \times 10^{-3} \mathrm{ ~ kg}$

c) $1.25 \times 10^{-3} \mathrm{ ~ kg}$

d) $5.0 \times 10^{-3} \mathrm{ ~ kg}$

Question 14- Benzene and toluene form nearly ideal solution. At $20^{\circ} \mathrm{C}$, the vapour pressure of benzene is 75 torr and that of toluene is 22 torr. The partial vapour pressure of benzene at $20^{\circ} \mathrm{C}$ in a solution containing $78 \mathrm{ ~ g}$ of benzene and $46 \mathrm{ ~ g}$ of toluene in torr is

a) $50.0$

b) $25.0$

c) $37.5$

d) $53.5$

Question 15- The mass of glucose that should be dissolved in $50 \mathrm{ ~ g}$ of water in order to produce the same lowering of vapour pressure as produced by dissolving $1 \mathrm{ ~ g}$ of urea in the same quantity of water is

a) $1 \mathrm{ ~ g}$

b) $3 \mathrm{ ~ g}$

c) $6 \mathrm{ ~ g}$

d) $8 \mathrm{ ~ g}$

Question 16- The relative lowering of vapour pressure of an aqueous solution containing non-volatile solute is 0.0125 . The molality of the solution is

a) $0.70$

b) $0.50$

c) $0.60$

d) $0.80$

Question 17- Two aqueous solutions $S _{1}$ and $S _{2}$ are separated by a semi-permeable membrane. $S _{2}$ has lower vapour pressure than $S _{1}$ of a non-volatile solute, Then

a) more solvent will flow from $S _{1}$ to $S _{2}$

b) more solvent will flow from $S _{2}$ to $S _{1}$

c) solvent from $S _{1}$ and $S _{2}$ will flow at equal rates

d) no flow will take place

Question 18- When $3 \mathrm{ ~ g}$ of a non-volatile hydrocarbon containing $94.4 \%$ carbon is dissolved in $100 \mathrm{ ~ g}$ benzene, the vapour pressure of benzene is lowered from $9.953 \mathrm{kPa}$ to $0.823 \mathrm{kPa}$. The molecular formula of the hydrocabon is

a) $\mathrm{C} _{7} \mathrm{H} _{5}$

b) $\mathrm{C} _{14} \mathrm{H} _{10}$

c) $\mathrm{C} _{5} \mathrm{H} _{7}$

d) $\mathrm{C} _{10} \mathrm{H} _{14}$

Question 19- A solution has 1:4 mole ratio of pentane to hexane. The vapour pressure of the pure hydrocarbons at $20^{\circ} \mathrm{C}$ are $440 \mathrm{ ~ mm} \mathrm{ ~ Hg}$ for pentane and $120 \mathrm{ ~ mm} \mathrm{ ~ Hg}$ for hexane. The mole fraction of pentane in the vapour phase is

a) 0.200

b) $0.478$

c) 0.549

d) $0.786$

PRACTICE QUESTIONS

Question 1- $200 \mathrm{ ~ mL}$ of an aqueous solution of a protein contains $1.26 \mathrm{ ~ g}$. The osmotic pressure of this solution at $300 \mathrm{ ~ K}$ is found to be $2.57 \times 10^{-3}$ bar. Molar mass of protein will be

a) $51022 \mathrm{ ~ g} \mathrm{ ~ mol}^{-1}$

b) $122044 \mathrm{ ~ g} \mathrm{ ~ mol}^{-1}$

c) $31011 \mathrm{ ~ g} \mathrm{ ~ mol}^{-1}$

d) $61038 \mathrm{ ~ g} \mathrm{ ~ mol}^{-1}$

Question 2- $100 \mathrm{cc}$ of $1.5 \%$ solution of urea is found to have an osmotic pressure of 6 atm and $100 \mathrm{cc}$ of $3.42 \%$ solution of cane sugar is found to have an osmotic pressure of $2.4 \mathrm{ ~ atm}$. If the two solution are mixed, osmotic pressure of resulting solution will be

a) $8.4 \mathrm{ ~ atm}$

b) $4.2 \mathrm{ ~ atm}$

c) $16.8 \mathrm{ ~ atm}$

d) $2.1 \mathrm{ ~ atm}$

Question 3- Which of the following $0.1 \mathrm{M}$ aqueous solution will have lowest freezing point?

a) Potassium Sulphate

b) Sodium chloride

c) Urea

d) Glucose

Question 4- $0.004 \mathrm{M} \mathrm{Na} _{2} \mathrm{SO} _{4}$ is isotonic with $0.01 \mathrm{M}$ glucose. Degree of dissociation of $\mathrm{Na} _{2} \mathrm{SO} _{4}$ is

a) $75 \%$

b) $50 \%$

c) $25 \%$

d) $85 \%$

Question 5- Freezing point of a solution containing $0.1 \mathrm{ ~ g}$ of $\mathrm{K} _{3}\left[\mathrm{Fe}(\mathrm{CN}) _{6}\right]$ (mol. wt. 239) in $100 \mathrm{ ~ g}$ of water $\left(\mathrm{K} _{\mathrm{r}}=1.86 \mathrm{ ~ K} \mathrm{ ~ kg} \mathrm{ ~ mol}^{-1}\right)$ is

a) $-2.3 \times 10^{-2}{ }^{0} \mathrm{C}$

b) $\quad 4 \times 10^{-5} \mathrm{C}$

c) $-5.7 \times 10^{-3}{ }^{0} \mathrm{C}$

d) $\quad 4 \times 10^{-6}{ }^{\circ} \mathrm{C}$

Question 6- A decimolar solution of potassium ferrocyanide is $50 \%$ dissociated at $300 \mathrm{ ~ K}$. Calculate the osmotic pressure of the solution.

a) $7.48 \mathrm{ ~ atm}$

b) $8.24 \mathrm{ ~ atm}$

c) $6.29 \mathrm{ ~ atm}$

d) $5.46 \mathrm{ ~ atm}$

Question 7- A motor vehicle radiator was filled with 8 litre of water in which 2 litre of a non-volatile solute (molar mass $32 \mathrm{ ~ g} \mathrm{ ~ mol}^{-1}$ ) was added. What is the lowest temperature at which the vehicle can be parked without a danger of freezing of water? $\left(\mathrm{K} _{\mathrm{f}}\right.$ of water $=1.86 \mathrm{ ~ K} \mathrm{ ~ kg} \mathrm{ ~ mol}^{-1}$ and density of methanol $=0.8 \mathrm{ ~ g} \mathrm{ ~ mL}^{-1}$ )

a) $\quad 11.625^{\circ} \mathrm{C}$

b) $-11.625^{\circ} \mathrm{C}$

c) $\quad 14.531^{\circ} \mathrm{C}$

d) $-14.531^{\circ} \mathrm{C}$

Question 8- The solutions $A, B, C$ and $D$ are respectively $0.1 \mathrm{M}$ glucose, $0.05 \mathrm{M} \mathrm{NaCl}, 0.05 \mathrm{M} \mathrm{BaCl} _{2}$ and $0.1 \mathrm{M} \mathrm{AICl} _{3}$. which one of the following pairs is isotonic?

a) $A \& C$

b) $B \& C$

c) $C \& D$

d) $A \& B$

Question 9- A solution containing $0.10 \mathrm{ ~ g}$ of non-volatile solute $X$ (molar mass $=100$ ) in $200 \mathrm{ ~ g}$ of benzene depresses the freezing point of benzene by $0.25^{\circ} \mathrm{C}$ while $0.50 \mathrm{ ~ g}$ of another non-volatile solute $\mathrm{Y}$ in $100 \mathrm{ ~ g}$ of benzene by $0.25^{\circ} \mathrm{C}$. What is the molar mass of $\mathrm{Y}$ ?

a) $50$

b) $100$

c) $150$

d) $1000$

Question 10- A solution containing $1.8 \mathrm{ ~ g}$ of a compound (empirical formula $\mathrm{CH} _{2} \mathrm{O}$ ) in $40 \mathrm{ ~ g}$ of water is observed to freeze at $-0.645^{\circ} \mathrm{C}$. The molecular formula of the compound is $\left(K _{\mathrm{f}}=1.86 \mathrm{ ~ kg} \mathrm{ ~ K}\right.$ $\mathrm{mol}^{-1}$ )

a) $\mathrm{C} _{2} \mathrm{H} _{4} \mathrm{O} _{2}$

b) $\mathrm{C} _{4} \mathrm{H} _{5} \mathrm{O} _{4}$

c) $\mathrm{C} _{5} \mathrm{H} _{10} \mathrm{O} _{5}$

d) $\mathrm{C} _{6} \mathrm{H} _{12} \mathrm{O} _{6}$

Question 11- $K _{\mathrm{f}}$ for water is $1.86 \mathrm{ ~ K} \mathrm{ ~ kg} \mathrm{ ~ mol}^{-1}$. If your automobile radiator holds $1.0 \mathrm{ ~ kg}$ of water, how many grams of ethylene glycol $\left(\mathrm{C} _{2} \mathrm{H} _{6} \mathrm{O} _{2}\right)$ must you add to get the freezing point of the solution lowered by $2.8^{\circ} \mathrm{C}$ ?

a) $27 \mathrm{ ~ g}$

b) $72 \mathrm{ ~ g}$

c) $93 \mathrm{ ~ g}$

d) $39 \mathrm{ ~ g}$

Question 12- Calculate the molal depression constant of a solvent which has freezing point $16.6^{\circ} \mathrm{C}$ and latent heat of fusion $180.75 \mathrm{ ~ J} \mathrm{ ~ g}^{-1}$.

a) $2.68$

b) $3.86$

c) $4.68$

d) $2.86$

Question 13- The freezing point of water is depressed by $0.37^{\circ} \mathrm{C}$ in a 0.01 molal NaCl solution. The freezing point of 0.02 molal solution of urea is depressed by.

a) $0.37^{\circ} \mathrm{C}$

b) $0.74^{\circ} \mathrm{C}$

c) $0.185^{\circ} \mathrm{C}$

d) $0^{\circ} \mathrm{C}$

Question 14- $0.004 \mathrm{M}$ solution of $\mathrm{Na} _{2} \mathrm{SO} _{4}$ is isotonic with $0.010 \mathrm{M}$ solution of glucose at the same temperature. The apparent degree of dissociation of $\mathrm{Na} _{2} \mathrm{SO} _{4}$ is.

a) $25 \%$

b) $50 \%$

c) $75 \%$

d) $85 \%$

Question 15- The freezing point depression constant of water is $1.86^{\circ} \mathrm{C} \mathrm{m}{ }^{-1}$. If $5.00 \mathrm{ ~ g}$ of $\mathrm{Na} _{2} \mathrm{SO} _{4}$ is dissolved in $45.0 \mathrm{ ~ g}$ of $\mathrm{H} _{2} \mathrm{O}$, the freezing point is found to be $-3.82^{\circ} \mathrm{C}$. Calculate the van’t Hoff factor for $\mathrm{Na} _{2} \mathrm{SO} _{4}$.

a) $0.381$

b) $2.05$

c) $2.63$

d) $3.11$

Question 16- $0.01 \mathrm{M}$ solution of $\mathrm{KCl}$ and $\mathrm{BaCl} _{2}$ are prepared in water. The freezing point of $\mathrm{KCl}$ solution is fount to be $-2^{\circ} \mathrm{C}$. What is the freezing point of $\mathrm{BaCl} _{2}$ solution, assuming complete lonization?

a) $-3^{0} \mathrm{C}$

b) $+3^{0} \mathrm{C}$

c) $-2^{0} \mathrm{C}$

d) $-4^{0} \mathrm{C}$

Question 17- Van’t Hoff factors of aqueous solution of $X, Y$ and $Z$ are $1.8,0.8$ and 2.5 respectively. Hence, correct order of the colligative property will be?

a) F.pt: $Y<X<Z$

b) V.P: $Y<X<Z$

c) B.pt: $Y<X<Z$

d) Osmotic pressure : $X=Y=Z$

Question 18- If osmotic pressure of $1 \mathrm{M}$ urea is $\pi$, what will be the osmotic pressure for $0.1 \mathrm{M} \mathrm{NaCl}$ ?

a) $\pi$

b) $0.1 \pi$

c) $2 \pi$

d) $0.2 \pi$

Question 19- Phenol associates in benzene to certain extent to form dimer. A solution containing $2.0 \mathrm{x}$ $10^{-2} \mathrm{ ~ kg}$ of phenol in $1.0 \mathrm{ ~ kg}$ of benzene has its freezing point decreased by $0.69 \mathrm{ ~ K}$. Calculate the degree of association of phenol ( $K _{\mathrm{f}}$ for benzene $\left.=5.12 \mathrm{ ~ K} \mathrm{ ~ kg} \mathrm{ ~ mol}^{-1}\right)$

a) $0.82$

b) $0.64$

c) $0.73$

d) $0.98$

Question 20- An aqueous solution containing $1.248 \mathrm{ ~ g}$ of barium chloride (molar mass $=208.34 \mathrm{ ~ g} \mathrm{ ~ mol}^{-1}$ ) in $100 \mathrm{ ~ g}$ of water boils at $100.0832^{\circ} \mathrm{C}$. Calculate the degree of dissociation of $\mathrm{BaCl} _{2}\left(K _{\mathrm{f}}\right.$ for water $=0.52 \mathrm{ ~ K} \mathrm{ ~ kg} \mathrm{ ~ mol}^{-1}$ )

a) $0.735$

b) $0.645$

c) 0.835

d) $0.555$