UNIT - 1 Solid State
Learning Objectives
After studying this unit, you will be able to
-
Differentiate between amorphous and crystalline solids
-
Explain the different types of crystalline solids based on the attractive forces between the particles
-
Differentiate between unit cell, crystal lattice and Bravais Lattices
-
Explain the close packing pattern in the solid state
-
Describe different types of voids present in the close packed structures
-
Calculate the packing efficiency of different types of cubic unit cells
-
Find the relation between the density of the substance and characteristics of its unit cell
-
Describe the imperfections present in the solids and explain their effect on some properties
-
Explain the range of electrical and magnetic properties exhibited by the solids
-
Explain the types of doping and their effect on the electrical properties
Solid State
-
One of the state of matter characterized by the rigidity of the constituent particles
-
Constituent particles have fixed positions and they can only oscillate about their mean position.
-
Constituent particles arranged in a regular pattern, the spatial arrangement is completely ordered (crystalline solid) unlike gaseous or liquid state.
-
Because of the highly ordered arrangement, solids have lower potential energy, so energy is required to convert solid to a liquid
-
Properties of the solids can be changed by adding some impurities or due to some structural imperfections or defects.
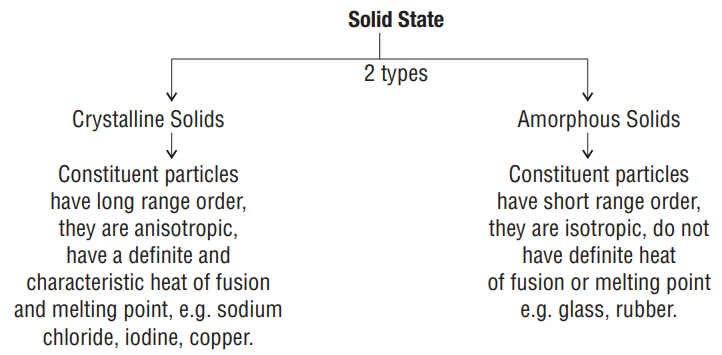
Classification of Crystalline solids
On the basis of nature of intermolecular forces
a) Ionic solids : - constituent particles are ions
-
coulombic or electrostatic forces exist between the ions
-
Insulators in solid state but conductors in molten state and in aqueous solutions
-
e.g. NaCl,
b) Metallic Solids : - Constituent particles are positive ions immersed in a sea of delocalized electrons.
-
Operative bonding between the ions is metallic
-
Conductors in solid state as well as in molten state
-
e.g.
c) Covalent Solids or Network Solids :
-
Constituent particles are atoms.
-
Covalent bonding between the atoms
-
Insulators, graphite is an exception
-
e.g. quartz, diamond
d) Molecular Solids: - Constituent particles are molecules
(3 types)
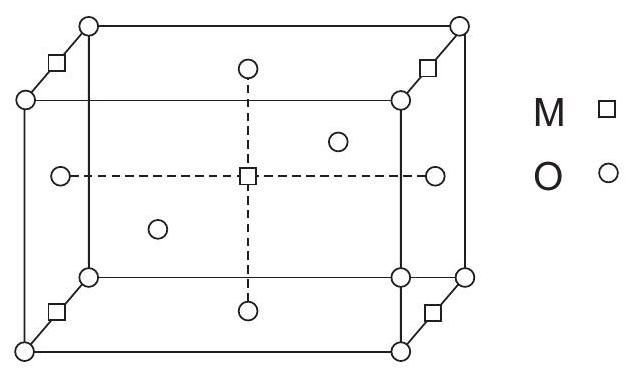
Regular arrangement of constituent particles of a crystal in a three dimensional space.
smallest portion of a crystal lattice which, when repeated in different directions, generates the entire lattice.
Six Parameters of unit cell:
3 - Edge lengths
3 - Angles between the edges -
Primitive simple unit cells (constituent particles are present only at corners)
Non-Primitive/centred unit cells
i). Body-centred - particles are present at the corners and body centre
ii). Face - Centred - particles are present at the corners and centre of each face.
iii). End centred - particles are present at the corners and centre of any two opposite faces.
Note: constituent particle may be an atom, a molecule (group of atoms) or an ion.
There are seven crystal systems and fourteen Bravais Lattice (Unit cells) corresponding to these seven crystal systems.
| Crystal System | Possible Variations | Axial/edge Lengths | Axial angles |
|---|---|---|---|
| Cubic | Primitive Body - centred Face - centred |
||
| Tetragonal | Primitive Body-centred |
||
| Orthorhombic | Primitive Body - centred Face - centred End - centred |
||
| Hexagonal | Primitive | ||
| Rhombohedral or Trigonal | Primitive | ||
| Monoclimic | End - centred |
||
| Triclinic | Primitive | ||
| Total |
Total |
Number of atoms in different unit cells:
Contribution of particles at
Corner
Edge Centre
| Cubic Unit cell | Total No. of atoms per unit cell |
|---|---|
| Simple cubic | |
| Body - centred Cubic | |
| Face - centred Cubic |
Coordination Number (C.No.): Number of nearest neighbours of a particle with which it is in contact with.
Packing of constituents in a crystal:
a). Close packing in 1-D - One type of arrangement is possible i.e. in a row C. No.
b). Close packing in 2-D
i). Square close packing
-
AAA type of arrangement
-
-
C.No.
ii). Hexagonal close packing
-
ABAB type of arrangement
-
-
C.No.
c). Close packing in 3-D
i) Hexagonal Close packed (hcp) - ABAB……. type of arrangement
ii) Cubic Close Packed (сcp) or face-centred cubic (fcc):
- ABCABC type of arrangement
- In both of these packings (hcp and ccp/fcc),
- C.No.
Note : In bcc, C. No. = 8
Empty spaces left in the close packed structures.
a) In 2-D Packing : Trigonal voids are present
b) In 3-D packing : Two types of voids
i) Tetrahedral void - Simple triangular void surrounded by 4 spheres.
C.No.
ii) Octahedral void - Double triangular void surrounded by six spheres
C.No.
In close packing the number of spheres
Number of octahedral voids
Number of tetrahedral voids
Tetrahedral void :
Octahedral void :
- Packing Fraction
-
Fraction of total space filled by the constituent particles.
Packing fraction
| Structure | Volume of the atom |
Packing density | ||
|---|---|---|---|---|
| Simple cubic | ||||
| hcp and ccp | ||||
| Body-centred cubic |
For lonic crystals, the formula used is the same.
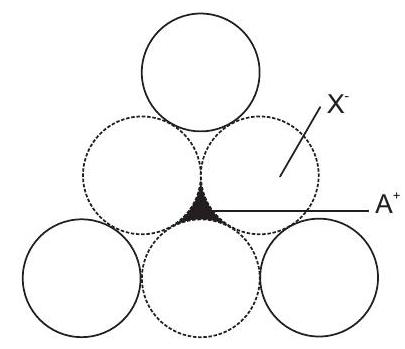
Radius Ratio
| Radius ratio | C.No. | Structural arrangement | Structure type | |
|---|---|---|---|---|
| 1. | 3 | Planar triangular | Boron oxide | |
| 2. | 4 | Tetrahedral | ||
| 3. | 6 | Octahedral | ||
| 4. | 8 | Body centred cubic |
| Crystal Structure | Arrangement of ions | Coordination number |
Formula units/ Unit cell |
|---|---|---|---|
| AB Type Rock Salt |
Clions = fcc arrangement centres and body centres |
4 | |
| Caesium Chloride (CsCl) type |
bcc arrangement |
1 | |
| Zinc Blende (ZnS) Type |
ccp arrangement tetrahedral voids |
4 | |
Flourite |
ccp arrangement |
4 | |
Antiflourite Type |
voids |
4 |
Effect of temperature and pressure on crystal structure
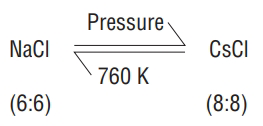
-
In
-
In ZnS, there are 8 tetrahedral voids, half of which are occupied by
-
In
- Irregularities in the arrangement of constituent particles
(a) Line defects / crystal defects: deviations from the ideal arrangement in entire rows of lattice points.
(b) Point defects : deviation from ideal arrangement around a point or an atom in a crystalline substance.
(a) Stoichiometric Defects
-
These defects are also known as Intrinsic or thermodynamic defects.
-
In this defect ratio between the cations and anions (stoichiometry) remain the same
i) Vacancy defect - When some of the lattice sites are vacant; density decreases in this defect.
ii) Interstitial defect - When some constituent particles occupy an interstitial site.
-
Density increases in this defect
-
Electrical Neutrality should be maintained
For Ionic Solids
iii) Frenkel defect / Dislocation defect:
-
Cations are missing from lattice site and occupy interstitial sites.
-
Occurs in compounds with low coordination number and large difference in size of cation and anions.
-
Density remains the same
-
e.g. Agl,
-
iv) Schottky defect -
-
Equal number of cations and anions are missing
-
Occurs in compounds having high coordination number and small difference in size of cations and anions.
-
Density decreases e.g. NaCl,
(b) Non stoichiometric defect: In this defect stoichiometriy does not remain the same
Two types
i) Metal Excess Defect
- Due to anionic vacancies - When crystals of alkali halides are heated in the vapour of alkali metal, some anions leave lattice sites in which electrons get trapped forming
LiCI Crystals - Pink Colour
KCI Crystals-Violet/Lilac Colour
(Due to the excess of alkali (Na, Li & K) metal)
- Due to the presence of extra cations at interstitial Sites:
White Yellow
ii) Metal Deficiency Defect - occurs when metal shows variable valency.
Few metal ions with lower valency are missing from their site but metal ions with higher valency are present at some sites thus balancing the charge. However, this leaves some vacancies at the sites of metal ions.
e.g.
(c) Impurity defect:
When foreign atoms are present at the lattice site in place of host atoms or at the vacant interstitial sites e.g.
- In this case cationic vacancies are produced which are equal to the number of
Electrical Properties - Solids shows a large range of electrical conductivities,
- Conductors - Valence band is partially filled or it overlaps with the conduction band, movement of electrons is easy. Conductivity is between
Conductivity decreases with the rise in temperature e.g. metals.
-
Semiconductors -
-
There is small enery gap between the valence and conduction band, some electrons may jump to the conduction band. Conductivity range
-
Conductivity increases with rise in temperature e.g.
-
-
Insulators
-
There is large energy gap between the valence and conduction band, electrons cannot jump to the conduction band.
-
Conductivity range
-
Doping
- Process of adding impurities to a crystalline substance to change its properties.
(a) n-types semiconductor - doping of group 14 elements (Si, Ge) with group 15 elements like P or As. Free electrons are present, responsible for increased conductivity.
(b) p-type semiconductor - Doping of group 14 elements with group 13 elements like B, Al & Ga.
Electron holes are created which are responsible for increased conductivity.
-
Act like semiconductors
-
These are formed by combination of group 13 and 15 elements.
-
e.g. InSb, AIP and GaAs
-
Act like semiconductors.
-
These are formed by combination of group 12 and 16 elements.
-
e.g. ZnS, CdS, CdSe and
(Show marked differences in electrical properties).
Magnetic Properties
1. Diamagnetic substances - Weakly repelled by magnetic field. They do not have unpaired electrons e.g.
2. Paramagnetic Substances - Attracted by magnetic field. They contain unpaired electrons e.g.
3. Ferromagnetic substances - show permanent magnetism even in the absence of magnetic field. All domains are aligned in one direction eg.
4. Anti-ferromagnetic substances - Domains are aligned in parallel and anti parallel directions in equal numbers. Net magnetic moment is zero e.g. MnO.
5. Ferrimagnetic substances - Domains are aligned in parallel and antiparallel directions in unequal numbers. These are weakly attracted by magnetic field. So, small net magnetic moment. e.g.
Solved Examples
Question 1. Experimentally it was found that a metal oxide has formula
(a)
(b)
(c)
(d)
Show Answer
Solution : (b)
Ratio of the numbers of
M:
Total
Because, oxide is neutral
Let, number of
so, number of
On equating the charge, we get
Hence, percentage of
Question 2. If
(a)
(b)
(c)
(d)
Show Answer
Solution : (d)
Number of cation vacancies produced by each
(a)
(b)
(c)
(d)
Show Answer
Solution (d).
Mass of the unit cell = Number of formula units in unit cell
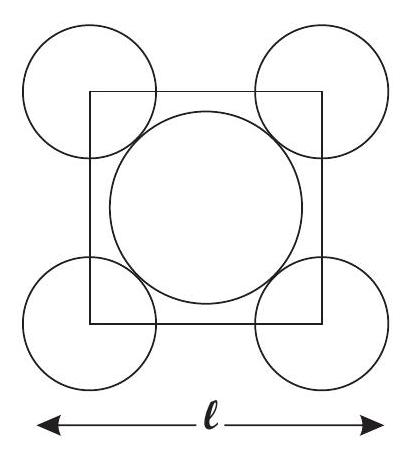
(a)
(b)
(c)
(d)
Show Answer
Solution (d).
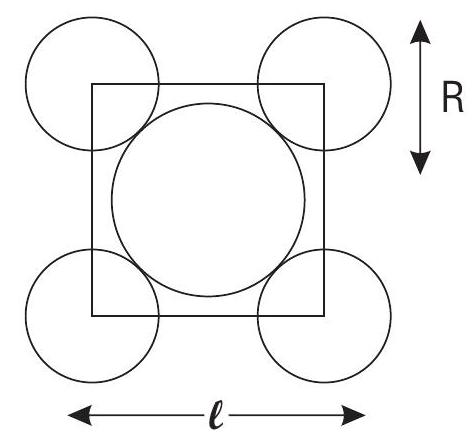
Contact between the spheres is along the diagonal.
Area of Square
Area of atoms present in 1 unit cell
Note : There are 2 atoms or effectively 2 circle in one unit cell.
PRACTICE QUESTIONS
Question 1. Structure of a mixed oxide is ccp. Cubic unit cell of mixed oxide is composed of oxide ions.
One Fourth of tetrahedral voids are occupied by divalent metal A and all the octahedral voids are occupied by monovalent metal
(a)
(b)
(c)
(d)
Show Answer
Answer:- bQuestion 2. In face centred cubic lattice, A occupies corners and B occupies face centres. If one atoms of
(a)
(b)
(c)
(d)
Show Answer
Answer:- cQuestion 3. No. of tetrahedral voids in the unit cell of a face centred cubic lattice of similar atoms is
(a) 4
(b) 6
(c) 8
(d) 12
Show Answer
Answer:- cQuestion 4. In a solid ’
(a)
(b)
(c)
(d)
Show Answer
Answer:- dQuestion 5. A substance
(a)
(b)
(c)
(d) composition cannot be specified
Show Answer
Answer:- aQuestion 6. An ionic crystalline solid
(a)
(b)
(c)
(d)
Show Answer
Answer:- aQuestion 7. Which of the following fcc structure contains cations in alternate tetrahedral voids?
(a)
(b) ZnS
(c)
(d)
Show Answer
Answer:- bQuestion 8. A compound
(a)
(b)
(c)
(d)
Show Answer
Answer:- bQuestion 9. If the positions of
(a)
(b)
(c) Number of
(d) The crystal structure of
Show Answer
Answer:- cQuestion 10. A compound consisting of the monovalent ions
(a)
(b)
(c)
(d)
Show Answer
Answer:- aQuestion 11.
Column I
(Distribution of particles
(a)
(b)
(c)
(d)
(a) A-r B-q, C-p, D-s
(b) A-s, B-p, C-r, D-q
(c) A-q, B-r, C-p, D-s
(d) A-r, B-q, C-s, D-p
Show Answer
Answer:- dQuestion 12.
Column I
(Position of particles
(a)
(b)
(c)
(d)
(a)
(b)
(c)
(d)
Show Answer
Answer:- dQuestion 13. If an atom is placed on each lattice point, the number of atoms per unit cell for primitive, body -centered cubic and face-centred cubic lattice, respectively, are ?
(a) 1,1 and 4
(b) 1,2 and 4
(c) 1,4 and 2
(d) 1,1 and 1
Show Answer
Answer:- bQuestion 14. A solid has a structure in which platinum ions are located at the corners of unit cell; oxide ions are located at the cube edges and sodium ions at the cube centres. The chemical composition of this solid is
(a)
(b)
(c)
(d)
Show Answer
Answer:- aQuestion 15. A compound of ’
(a)
(b)
(c)
(d)
Show Answer
Answer:- dQuestion 16. Arrangement of
(a)
(b)
(c)
(d)
Show Answer
Answer:- dQuestion 17. The arrangement of
(a)
(b)
(c)
(d)
Show Answer
Answer:- aQuestion 18. If spheres of radius ’
(a)
(b)
(c)
(d)
Show Answer
Answer:- aQuestion 19. The number of atoms in
(a)
(b)
(c)
(d)
Show Answer
Answer:- aQuestion 20. Ice crystallises in a hexagonal lattice having a volume of the unit cell as
(a) 1
(b) 2
(c) 3
(d) 4
Show Answer
Answer:- dQuestion 21. The edge length of a face centered cubic cell of an ionic substance is
(a)
(b)
(c)
(d)
Show Answer
Answer:- aQuestion 22. Percentages of free space in cubic close packed structure and in body centred packed structure are respectively
(a)
(b)
(c)
(d)
Show Answer
Answer:- cQuestion 23. Copper crystallizes in fcc with a unit cell length of
(a)
(b)
(c)
(d)
Show Answer
Answer:- cQuestion 24. Number of unit cells in
(a)
(b)
(c)
(d)
Show Answer
Answer:- cQuestion 25. In an ionic compound
(a)
(b)
(c)
(d)
Show Answer
Answer:- dQuestion 26. Schottky defect in crystals is observed
(a) when unequal number of cations and anions are missing from the lattice
(b) when equal number of cations and anions are missing from the lattice
(c) when the density of the crystal is increased
(d) when an ion leaves its normal site and occupies an interstitial site.
Show Answer
Answer:- bQuestion 27. The colours of some otherwise colourless compounds are due to
(a) Frenkel defect
(b) Metal deficiency defect
(c) Schottky defect
(d) Metal excess defect (F-Centres)
Show Answer
Answer:- dQuestion 28. Crystal with metal deficiency defect is
(a)
(b)
(c)
(d)










