Unit 08 Redox Reactions
Any reaction in which electrons are exchanged between atoms or ions, represents simultaneous process of oxidation and reduction and is called a Redox reaction.
Oxidation is
(i) the gain of oxygen
or (ii) the loss of hydrogen
or (iii) the loss of electrons (de-electronation)
or (iv) the increase in oxidation number
Reduction is (the reverse of oxidation)
(i) the loss of oxygen
or (ii) the gain of hydrogen
or (iii) the gain of electron (electronation)
or (iv) the decrease in oxidation number
Electronic concept of Oxidation and Reduction:
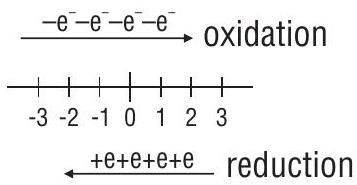
Loss of electrons is called Oxidation
Gain of electrons is called Reduction
Redox Reaction
A reaction in which oxidation and reduction are carried out simultaneously is called redox reaction. One substance undergoes oxidation and other substance undergoes reduction i.e. reaction between a reducing agent and oxidising agent is termed as redox reaction.
Reducing agent
Redox Reactions are divided into two main types :
(i) Intermolecular redox reaction: In such a redox reaction, molecule of one reactant is oxidised whereas the molecule of other reactant gets reduced.
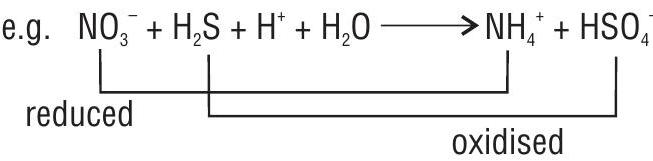 (ii) Intramolecular redox reaction : In this case one atom of a molecule is oxidised and the other atom of the same molecule gets reduced.
(ii) Intramolecular redox reaction : In this case one atom of a molecule is oxidised and the other atom of the same molecule gets reduced.
Oxidation Number of Elements in Covalent Compound and in Ions:
Rules for Assigning Oxidation Number (O.N.)
Oxidation Number of one particular element in a covalent compound or ion is determined by taking the Oxidation Number of other elements according to certain rules which are summarised below
Wherever there is doubt, the more electro-negative atom takes the lower oxidation number.
In neutral molecules, sum of oxidation numbers is zero.
In ions, sum of oxidation numbers is equal to charge.
While naming the ion or compound, it is desirable to put oxidation number per atom (i.e. oxidation state) in roman figures within brackets. (anion ends with ate)
Oxidation number of an atom is also called its oxidation state
If central atom is in the highest oxidation state in a compound it behaves as an oxidising agent (eg.
Note: In an organic compound containing carbon, hydrogen and oxygen, the oxidation number of carbon can be calculated as,
Oxidation number of carbon
Where,
Examples:
(I).
Here two 0 -atoms form peroxide linkage, i.e.,
(ii)
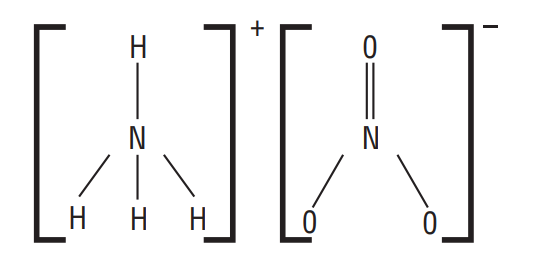
No doubt there are two
Oxidation Number of
(iii)
The above oxidation number of I in
Average 0.N.
(iv)
This is the average oxidation number:
The structure of
The O.N. of
(v)
Exceptional cases of calculation of oxidation numbers
The rules described earlier are usually helpful in determination of the oxidation number of a specific atom in simple molecules but these rules fail in following cases. In these cases, the oxidation numbers are evaluated using the concepts of chemical bonding involved.
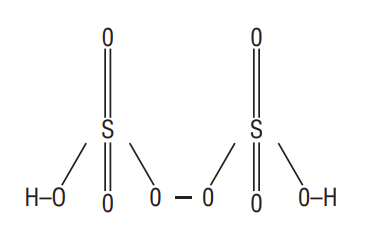
Type I. In molecules containing peroxide linkage in addition to element-oxygen bonds. For example,
(i) Oxidation number of
(Permonosulphuric acid or Caro’s acid)
By usual method;
But this cannot be true as maximum oxidation number for
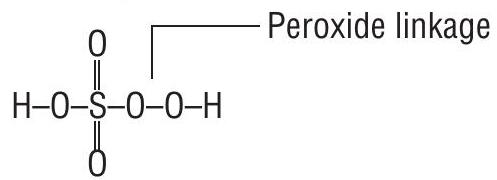
Therefore the evaluation of
(for
or
(ii) Oxidation number of
(Peroxidisulphuric acid or Marshall’s acid)
By usual method:
Similar to Caro’s acid, Marshall’s acid also has a peroxide linkage and

Therefore the evaluation of oxidation state of sulphur should be made as follows,
or
(iii) Oxidation number of
(Blue perchromate)
By usual method
This cannot be true as maximum O.N. of Cr cannot be more than +6 , since
The chemical structure of
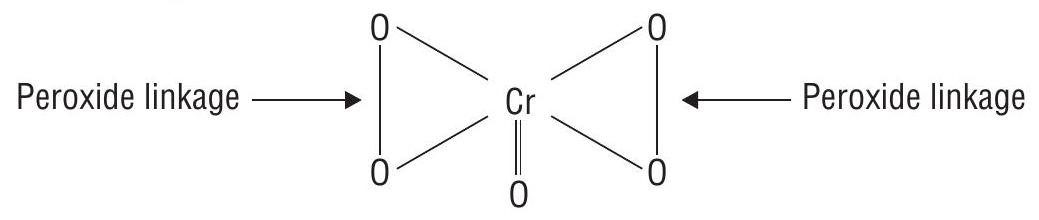
Therefore, the evaluation of
(for Cr) (for 0) (for 0-0)
or
Type II. In molecules containing covalent and coordinate bonds, following rules are used for evaluating the oxidation numbers of atoms.
(i) For each covalent bond between dissimilar atoms the less electronegative element is assigned the oxidation number of +1 while the atom of the more electronegative element is assigned the oxidation number of -1 .
(ii) In case of a coordinate-covalent bond between similar or dissimilar atoms but the donor atom is less electronegative than the acceptor atom, an oxidation number of +2 is assigned to the donor atom and an oxidation number of -2 is assigned to the acceptor atom.
Conversely, if the donor atom is more electronegative than the acceptor atom, the contribution of the coordinate bond is neglected. Examples.
(a) Oxidation number of
The evaluation of oxidation number of
In such cases, evaluation of oxidation number should be made using indirect concept or by the original concepts of chemical bonding.
(i) Oxidation number of carbon in
The contribution of coordinate bond is neglected since the bond is directed from a more electronegative
Therefore the oxidation number of
(for
or
(ii) Oxidation number of carbon in
In
Now
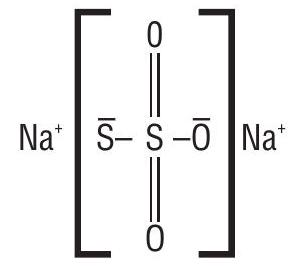
Type III. In a molecule containing two or more atoms of same or different elements in different oxidation states.
(i) Oxidation number of
By usual method
or
But this is unacceptable as the two sulphur atoms in
In this case, the oxidation number of sulphur is revaluated, from concepts of chemical bonding. The chemical structure of
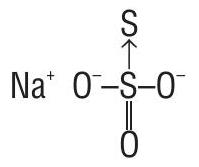
Due to the presence of a co-ordinate bond between two sulphur atoms, the acceptor sulphur atom has oxidation number of -2 whereas the other
or
Thus two sulphur atoms in
(ii) Oxidation number of chlorine in
In bleaching powder
(iii) Oxidation number of
By usual method
No doubt
(iv) Oxidation number of
In
(v) Oxidation number of
Its structure can be represented as follows,
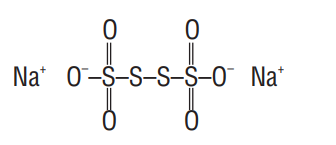
The two S-atoms which are linked to each other have oxidation number zero. The oxidation number of other
Let oxidation number of
(for S) (for S-S) (for 0 )
APPLICATIONS OF OXIDATION STATE
If an element is in its highest possible oxidation state in a compound, it can act only as an oxidising agent, for example,
If element is in its lowest oxidation state in a compound, it can act only as a reducing agent. For example,
The strength of oxyacids of chlorine decrease in the order.
If an element is in intermediate oxidation state in a compound, it can act both as an oxidising as well as a reducing agent. For example,
Difference between Valency and Oxidation Number :
| Valency | Oxidation number | ||
|---|---|---|---|
| 1. | Combining capacity of the element | i. | Charge (real or imaginary) present on the atom in a compound |
| 2. | Usually fixed | ii. | Has different values |
| 3. | Always a whole number | iii. | May be fractional also |
| 4. | Never zero | iv. | May be zero also |
Types of redox reactions:
1. Combination reactions:
2. Decomposition Reactions : (Reverse of combination reaction)
3. Displacement reactions
Metal displacement:
Non-metal displacement
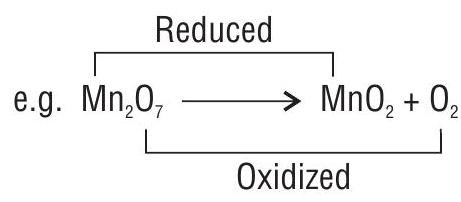
4. Disproportionation:
It is a special type of redox reaction in which an element in a particular oxidation state gets simultaneously oxidised and reduced.
oxidation state of 0 changes from -1 to 0 and -2 state.
5. Auto-oxidation
Certain materials such as terpentine, olefinic compounds, phosphorus, metals like zinc and lead etc. can absorb oxygen from the air in the presence of water and water gets converted to hydrogen peroxide refers to the phenomenon of auto-oxidation. The material which absorbs oxygen and activates this is called the activator. The addition compound of activator and oxygen is termed as auto-oxidator. This reacts with water or some other acceptor so as to oxidise the latter.
BALANCING OXIDATION-REDUCTION REACTIONS BY OXIDATION NUMBER METHOD :
The steps involved are:
(i) The skeleton equation of the chemical change is written.
(ii) Oxidation numbers are assigned to atoms in the equation. The atoms in which change in oxidation number has taken place are selected and two half reactions involving oxidation and reduction are selected.
(iii) Change in oxidation numbers in both the equations is made equal by multiplying with suitable integers and then both the equations are added.
(iv) First of all, those substances are balanced which have undergone change in oxidation number and then other atoms except hydrogen and oxygen. Finally hydrogen and oxygen are balanced. In ionic equations, the net charges on both sides are made equal.
ION-ELECTRON METHOD FOR BALANCING REDOX REACTIONS
The method for balancing redox reactions by ion electron method was developed by Jette and LaMev in 1927. It involves the following steps:
(i) Write down the redox reaction in ionic form.
(ii) Split the redox reaction into two half reactions, one for oxidation and the other for reduction.
(iii) Balance each half reaction for the number of atoms of each element. For this purpose:
(a) Balance the atoms other than
(b) Add water molecules to the side deficient in oxygen and
(c) In alkaline solution, for each excess of oxygen, add one water molecule to the same side and
(iv) Add electrons to the side deficient in electrons as to equalise the charge on both sides.
(v) Multiply one or both the half reactions by a suitable number so that the numbers of electrons become equal in both the equations.
(vi) Add the two balanced half reactions and cancel any term common to both sides.
The following solved problems illustrate the various steps in oxidation number method.
1. Balance the given reaction by using oxidation number method.
The balancing is done in the following steps:
Write the Oxidation Number of each atoms in the skeleton equation.
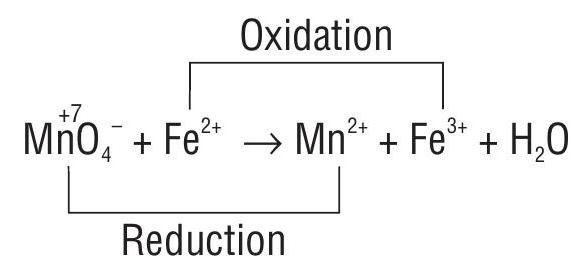
Identify the atoms which undergo change in oxidation number.
Calculate the increase and decrease in oxidation number w.r.t. reactant atoms.
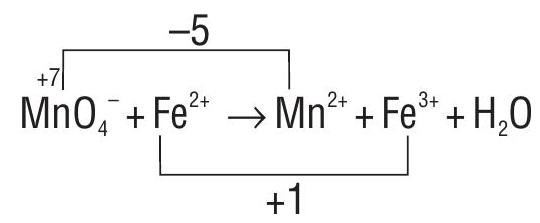
Equate the increase and decrease in oxidation number on the reactant side.
Balance Mn and Fe atoms on both sides of the equation.
As the reaction is carried in the acidic medium, to balance 0 atoms, add three
2. Balance the given reaction in basic medium.
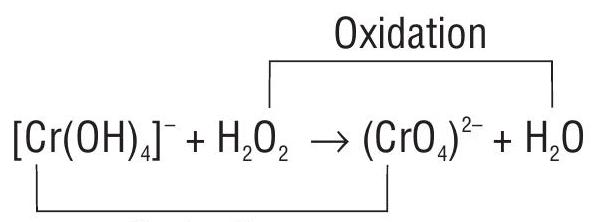
Reduction
- Write the Oxidation number of each atom
Calculate the increase and decrease in oxidation number.
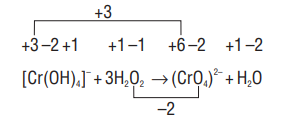
Equate the increase and decrease in oxidation number on the reactant side
Balance the number of
In order to balance the number of oxygen atoms, add five
As the reaction is carried in the basic medium, in order to balance the number of negative charges add two
or
Example for balancing using lon electron method
Oxidation half reaction.
Reduction half reaction
Equate electrons lost and gained and add
PRACTICE QUESTIONS
1. Balance the following equations:
(i)
Show Answer
Answer:(ii)
Show Answer
Answer:(iii)
Show Answer
Answer:(iv)
Show Answer
Answer:(v)
Show Answer
Answer:(vi)
Show Answer
Answer:(vii)
Show Answer
Answer:(viii)
Show Answer
Answer:(ix)
Show Answer
Answer:(x)
Show Answer
Answer:PRACTICE QUESTIONS
1. In the reaction,
(a) It is a redox reaction.
(b) Metallic iron is a reducing agent.
(c)
(d) Metallic iron is reduced to
Show Answer
Answer: (d)2. The oxidation number of chlorine in
(a) -1
(b) zero
(c) +1
(d) +2
Show Answer
Answer: (c)3. For the redox reaction,
the correct coefficients of the reactants for the balanced equation are :
Show Answer
Answer: (a)4. Which one of the following is not a redox reaction?
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)5. The oxidation state of iodine in
(a) +7
(b) -1
(c) +5
(d) +1
Show Answer
Answer: (a)6. The oxide which cannot act as a reducing agent is :
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)7. In a chemical reaction,
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)8. When copper is treated with a certain concentration of nitric acid, nitric oxide and nitrogen dioxide are liberated in equal volumes according to the equation,
The coefficients
(a) 2,3
(b) 2,6
(c) 1,3
(d) 3,8
Show Answer
Answer: (b)9. Amongst the following, identify the species with an atom in +6 oxidation state :
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)10. The reaction,
is an example of
(a) oxidation reaction
(b) reduction reaction
(c) disproportionation reaction
(d) decomposition reaction
Show Answer
Answer: (c)11. The oxidation state of iodine in
(a) +1
(b) +3
(c) +5
(d) +7
Show Answer
Answer: (b)12. In alkaline medium,
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)13. Which of the following chemical reactions depict the oxidising behaviour of
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)14. Oxidation state of oxygen in
(a) 3,2
(b) 1,0
(c) 0,1
(d)
Show Answer
Answer: (d)15. The reaction,
(a) disproportionation reaction
(b) neutralisation reaction
(c) double decomposition reaction
(d) pyrolytic reaction
Show Answer
Answer: (a)16. Match the items in list ’
| List A | List B | ||
|---|---|---|---|
| a. | p. | Redox reaction | |
| b. | q. | Zero oxidation number | |
| c. | r. | Simple neutralisation reaction | |
| d. | s. | Natural redox reaction | |
| e. | t. | Fractional oxidation number | |
| f. | Photosynthesis | u. | Disproportionation reaction |
Show Answer
Answer: a-u, b-p, c-t, d-q, e-r, f-sREDOX TITRATIONS
There are two approaches to analyse a redox reaction
(I) mole-concept
(ii) gram or milli equivalents (meq)
Mole Concept
First balance a given redox reaction then simply apply mole-concept.
from stoichiometry of reaction
n mole of
millimoles
or Moles
Question. 1
Show Answer
Solution:
millimoles of
Mass of
GRAM EQUIVALENTS
In this method there is no need to balance a redox reaction
Reducing
agent
meq of
meq
Eq. mass
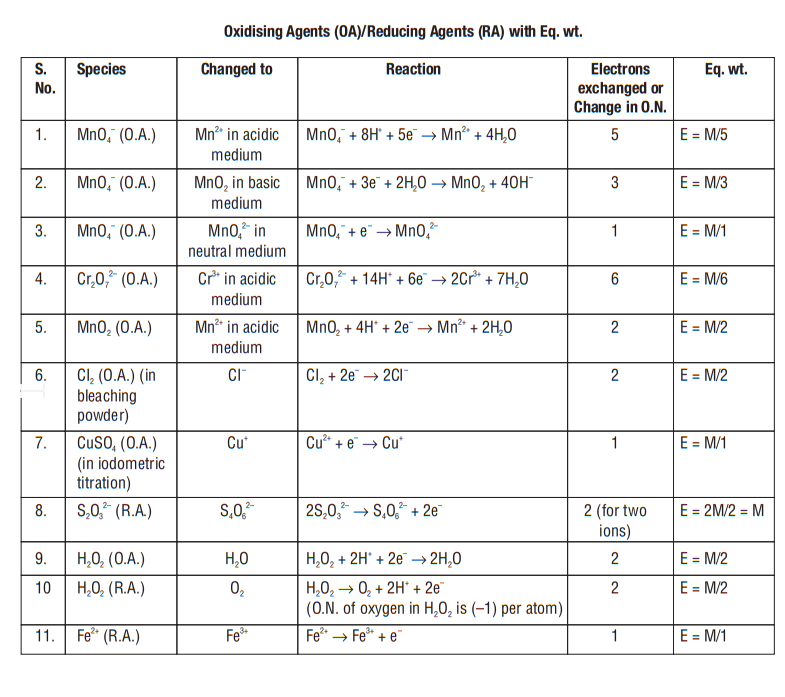

EXAMPLES
1.
As a reducing agent
2.
As a reducing agent (Acidic medium)
for one mole
As a reducing agent (Basic medium)
3.
As an oxidant (conc.
As an oxidant (dil
Note: Equivalent mass depends on dilution
Question.2
Show Answer
Solution:
only
Therefore weight of
Moles of
Question.3 An element
Show Answer
Solution:
meg of
Question.4
(a) Purity of
(b) Volume of dry
Show Answer
Solution:
meq of
(b) Now eq. of
(applying PV=nRT)
therefore
Question. 5
Show Answer
Solution: The calculations involve the following steps
(i)
(ii) Excess
(iii) To determine molarity of
(iv) To determine percentage of
Firstly we have to balance eq(ii)
The overall balanced equation is
milli moles of
Here,
Let ’
or
Question. 6 A solution of
Show Answer
Solution
Also
The mole ratio is
PRACTICE QUESTIONS
1. What volume of
(a)
(b)
(c) 0.56 litre
(d) 1.12 litre
Show Answer
Answer: (b)2. What volume of
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)3. What is the normality of
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)4. What volume of
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)5. For the reaction,
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)6. In alkaline condition
The equivalant weight of
(a) 52.7
(b) 158
(c) 31.6
(d) 79
Show Answer
Answer: (b)7. A solution of
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)8. Number of
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)9. A solution containing
(a) 1
(b) 2
(c) 3
(d) 4
Show Answer
Answer: (b)10.
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)11. Column I lists equivalent masses and column II lists some of the typical titrations. Match each entry of column I with those given in Column II.
Show Answer
Answer: a-q, b-t, c-s, d-r12.
(a)
(b)
(c)
(d)
Passage
Orange
In alkaline solution, orange colour of
Orange
When
A deep blue violet coloured peroxo compound,
Show Answer
Answer: (c)13. Number of moles of
(a)
(b) 3
(c)
(d) 6
Show Answer
Answer: (a)14. The equivalent weight of
(a) 137.34
(b) 84.44
(c) 114.45
(d) 68.67
Show Answer
Answer: (b)15. The equivalent mass of
(a)
(b)
(c)
(d)










