It is the study of equilibrium in the reactions where formation of ions takes place in aqueous solutions. The compounds which gives ions either in molten state or in solution are called electrolytes. The compound can be ionic (e.g. NaCl, ${\mathrm{KNO}}_3,\mathrm{NaOH}$ etc) or polar covalent (e.g. $\mathrm{HCl},\mathrm{HCN},{\mathrm{NH}}_3,{\mathrm{CH}}_3\mathrm{COOH}$ etc).

These electrolytes can be classified as

(i) Strong electrolytes

These electrolytes are almost completely ionised i.e. extent of dissociation is high $(\alpha \to 1)$. Therefore, the concept of equilibrium doesnot arise in such cases. These solutions behave as very good conductors of electricity.

(ii) Weak electrolytes

These electrolytes dissociate in a solution to a small extent. The extent of dissociation is much less than one. These solution are poor conductors of electricity.

Note: This classification of electrolytes is based on their behaviour only in water as solvent.

The weak electrolytes can be categorized into three types

(a) Weak acids : ${\mathrm{CH}}_3\mathrm{COOH},\mathrm{HCN}$ (and all organic acids)

(b) Weak bases : ${\mathrm{NH}}_4\mathrm{OH}$ and all organic bases

(c) Sparingly soluble salts: ${\mathrm{AgCl}}_2{\mathrm{PbCl}}_2,{\mathrm{Ag}}_2{\mathrm{CrO}}_4$ etc.

Weak acids and weak bases

Consider ionisation of a weak electrolyte say a monoprotic acid, HA

$\begin{array}{llllll}& \mathrm{HA}(\mathrm{aq})+{\mathrm{H}}_2\mathrm{O}(\mathrm{l})& \rightleftharpoons & {\mathrm{H}}_3\mathrm{O}& (\mathrm{aq})& +{\mathrm{A}}^{-}(\mathrm{aq})\\ \text{or}& \mathrm{HA}& \rightleftharpoons & {\mathrm{H}}^{+}& +& {\mathrm{A}}^{-}\\ \text{Moles before dissociation}& 1& & 0& & 0\\ \text{Moles after dissociation}& 1-\alpha & & \alpha & & \alpha \end{array}$

where, $\alpha$ is degree of dissociation of weak acid HA. Let ’ $c$ ’ mol litre ${}^{-1}$ be concentration of acid $\mathrm{HA}$, then

$[HA]=c(1-\alpha );\left[H^{+}\right]=c\alpha ;\left[A^{-}\right]=c\alpha$

According to the law of equilibrium

$K_a=\frac{\left[H^{+}\right]\left[A^{-}\right]}{[HA]}=\frac{c\alpha \cdot c\alpha }{c(1-\alpha )}$

${\mathrm{K}}_{\mathrm{a}}=\frac{c{\alpha }^2}{(1-\alpha )}$

where, ${\mathrm{K}}_{\mathrm{a}}$ is dissociation constant of the acid. Since for weak electrolytes ’ $\alpha$ ’ is small and thus,

$1-\alpha =1$

${\mathrm{K}}_{\mathrm{a}}=\mathrm{C}{\alpha }^2\text{ or }\alpha =\sqrt{\frac{{\mathrm{K}}_{\mathrm{a}}}{\mathrm{c}}}=\sqrt{{\mathrm{K}}_{\mathrm{a}}\mathrm{V}}$

where, $\mathrm{V}$ is the volume in litre containing 1 mole of electrolyte.

Thus, degree of dissociation increases on dilution and this is known as Ostwald dilution law Similar expression can also be derived for a weak base $\mathrm{BOH}$ as,

$\begin{array}{rl}& \mathrm{BOH}\rightleftharpoons {\mathrm{B}}^{+}+{\mathrm{OH}}^{-}\\ & {\mathrm{K}}_{\mathrm{b}}=\frac{\mathrm{c}{\alpha }^2}{1-\alpha }\end{array}$

If $1-\alpha =1,{\mathrm{K}}_{\mathrm{b}}=\mathrm{c}{\alpha }^2$

$\text{ or }\alpha =\sqrt{\frac{{\mathrm{K}}_{\mathrm{b}}}{\mathrm{c}}}$

where, ${\mathrm{K}}_b$ is dissociation constant of the base.

The ion ${\mathrm{A}}^{-}$formed during ionisation of $\mathrm{HA}$ is termed as its conjugate base and the ion ${\mathrm{B}}^{+}$ formed during ionisation of $\mathrm{BOH}$ is termed as its conjugate acid.

${\mathrm{H}}_2{\mathrm{PO}}_4^{-}$: Its conjugate acid is ${\mathrm{H}}_3{\mathrm{PO}}_4$ and its conjugate base is ${\mathrm{HPO}}_4{}^{2-}$

At a given temperature ${\mathrm{K}}_{\mathrm{a}}$ and ${\mathrm{K}}_b$ are directly proportional to degree of dissociation ( $\alpha$ ) therefore by comparing $K_a$ (or $K_b$ ) of different acids (or bases) their strengths can be compared

$$ i.e. $\frac{{\alpha }_1}{{\alpha }_2}=\sqrt{\frac{K_a}{K_a}}$

ACIDS AND BASES

Arrhenius Concept (1880 - 1890)

i. An Arrhenius acid is a substance which furnishes hydrogen ions ( ${\mathrm{H}}^{+}$ions) in aqueous solution,

$\mathrm{HCl}\to {\mathrm{H}}^{+}+{\mathrm{Cl}}^{-}(\text{ strong acid })$

${\mathrm{CH}}_3\mathrm{COOH}\rightleftharpoons {\mathrm{CH}}_3{\mathrm{COO}}^{-}+{\mathrm{H}}^{+}(\text{weak acid })$

ii. An Arrhenius base is a substance which furnishes hydroxyl $\left({\mathrm{OH}}^{-}\right)$ions in aqueous solution, e.g.,

$\begin{array}{lr}\mathrm{NaOH}\to {\mathrm{Na}}^{+}+{\mathrm{OH}}^{-}& \text{(strong base) }\\ {\mathrm{NH}}_4\mathrm{OH}\rightleftharpoons {\mathrm{NH}}_4^{+}+{\mathrm{OH}}^{-}& \text{(weak base) }\end{array}$

iii. The strength of an acid or base depends upon its tendency to furnish ${\mathrm{H}}^{+}$or ${\mathrm{OH}}^{-}$ions in solution, respectively.

iv. Water is amphoteric because it furnishes both ${\mathrm{H}}^{+}$and ${\mathrm{OH}}^{-}$ions in solution

${\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{H}}^{+}+{\mathrm{OH}}^{-}$

Limitations of Arrhenius concept

i. If fails to explain the behaviour of acids and bases in non-aqueous solvents.

ii. If fails to explain the neutralisation reactions giving rise to salt formation in absence of solvent.

e.g., ${\mathrm{CO}}_2+\mathrm{CaO}\to {\mathrm{CaCO}}_3$;

${\mathrm{NH}}_3(\mathrm{g})+\mathrm{HCl}(\mathrm{g})\to {\mathrm{NH}}_4\mathrm{Cl}(\mathrm{g})\text{ or }(\mathrm{s})$

Bronsted-Lowry Concept (1923)

i. A Bronsted acid is proton donor whereas, a Bronsted base is proton acceptor.

ii. The strength of the acids / bases depends upon the tendency to donate / accept the proton.

iii. Water is amphoteric because it donates as well as accepts proton.

iv. A pair of Bronsted acid-base which differ by a proton is known as conjugate pair of Bronsted acid and Bronsted base

Substance $+{\mathrm{H}}^{+}$ion $=$Conjugate acid

Substance $-{\mathrm{H}}^{+}$ion $=$Conjugate base

$\begin{array}{lll}\text{Conjugate base}& \text{Substance}& \text{Conjugate acid}\\ {\mathrm{OH}}^{-}& {\mathrm{H}}_2\mathrm{O}& {\mathrm{H}}_3{\mathrm{O}}^{+}\\ {\mathrm{C}}_2{\mathrm{H}}_5{\mathrm{O}}^{-}& {\mathrm{C}}_2{\mathrm{H}}_5\mathrm{OH}& {\mathrm{C}}_2{\mathrm{H}}_5\stackrel{+}{\mathrm{O}}{\mathrm{H}}_2\\ {\mathrm{NH}}_2^{-}& {\mathrm{NH}}_3& {\mathrm{Nh}}_4^{+}\end{array}$

Limitations

It does not explain the reactions between acidic oxides and basic oxides.

$$\mathrm{CaO}+{\mathrm{CO}}_2\to {\mathrm{CaCO}}_3$$

basic oxide acidic oxide

There is neither loss nor gain of a proton.

It could not explain the acidic nature of ${\mathrm{BF}}_3,{\mathrm{AICl}}_3$ etc.

Dissociation constant of conjugate acid-base pair

Let us consider, dissociation of weak acid HA in aqueous medium

$\mathrm{HA}\rightleftharpoons {\mathrm{H}}^{+}+{\mathrm{A}}^{-}$

Acid $$ Conjugate base

$K_a=\frac{\left[H^{+}\right]\left[A^{-}\right]}{[HA]}$ (i)

Dissociation constant of conjugate base ${\mathrm{A}}^{-}$may be calculated as

$$\begin{array}{rl}& {\mathrm{A}}^{-}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons \mathrm{HA}+{\mathrm{OH}}^{-}\\ \text{(ii)}& & {\mathrm{K}}_{\mathrm{b}}=\frac{[\mathrm{HA}]\left[{\mathrm{OH}}^{-}\right]}{\left[{\mathrm{A}}^{-}\right]}\end{array}$$

From eqns. (i) and (ii)

$$\begin{array}{rl}& {\mathrm{K}}_{\mathrm{a}}{\mathrm{K}}_{\mathrm{b}}=\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{OH}}^{-}\right]\\ \text{(iii)}& & {\mathrm{K}}_{\mathrm{a}}{\mathrm{K}}_{\mathrm{b}}={\mathrm{K}}_{\mathrm{w}}\end{array}$$

where ${\mathrm{K}}_{\mathrm{w}}={10}^{-14}$ at ${25}^{\circ }\mathrm{C}$

Taking logarithm of Eqn. (iii)

$$\begin{array}{rl}& {\log }_{10}{\mathrm{K}}_{\mathrm{a}}+{\log }_{10}{\mathrm{K}}_{\mathrm{b}}={\log }_{10}{\mathrm{K}}_{\mathrm{w}}\\ & -{\log }_{10}{\mathrm{K}}_{\mathrm{a}}-{\log }_{10}{\mathrm{K}}_{\mathrm{b}}=-{\log }_{10}{\mathrm{K}}_{\mathrm{w}}\\ & {\mathrm{pK}}_{\mathrm{a}}+{\mathrm{pK}}_{\mathrm{b}}={\mathrm{pK}}_{\mathrm{w}}\\ & {\mathrm{pK}}_{\mathrm{w}}=14\mathrm{at}{25}^{\circ }\mathrm{C}\end{array}$$

$\text{ or }{\mathrm{pK}}_{\mathrm{a}}+{\mathrm{pK}}_{\mathrm{b}}=14$

Lewis concept (1939)

A base is defined as a substance which can furnish a pair of electrons to form a coordinate bond whereas an acid is a substance which can accept a pair of electrons.

i) ${\mathrm{H}}_3\mathrm{N}:+{\mathrm{BF}}_3={\mathrm{H}}_3\mathrm{N}\to {\mathrm{BF}}_3$ base acid

ii) ${\mathrm{H}}^{+}+:{\mathrm{NH}}_3={[\mathrm{H}\to {\mathrm{NH}}_3]}^{+}$ acid base

iii) ${\mathrm{BF}}_3+[\mathrm{F}{]}^{-}={[\mathrm{F}\to {\mathrm{BF}}_3]}^{-}$

acid base

Lewis acids are

i. Molecules in which the central atom has incomplete octet:

${\mathrm{BF}}_3,{\mathrm{BCl}}_3,{\mathrm{AlCl}}_3,{\mathrm{MgCl}}_2,{\mathrm{BeCl}}_2$ etc.

ii. Simple cations:

${\mathrm{Na}}^{+},{\mathrm{K}}^{+},{\mathrm{Ca}}^{2+},{\mathrm{H}}^{+},{\mathrm{Ag}}^{+}$etc.

iii. Molecules in which the central atom has empty d-orbitals :

The central atom of the halides such as ${\mathrm{SiX}}_4,{\mathrm{GeX}}_4,{\mathrm{TiCl}}_4,{\mathrm{SnX}}_4,{\mathrm{PX}}_3,{\mathrm{PF}}_5,{\mathrm{SF}}_4,{\mathrm{SeF}}_4,{\mathrm{TeCl}}_4$ etc. have vacant d-orbitals.

iv. Molecules having a multiple bond between atoms of dissimilar electronegativity:

Typical examples of molecules

$$\bigcap _{\text{ Lewis acid }}=0+\underset{\text{ Lewis base }}{{\mathrm{OH}}^{-}}\mathrm{O}-{\mathrm{CH}}^{\mathrm{OH}}=0\text{ or }{\mathrm{HCO}}_3^{-}$$

Lewis Bases are

i. Neutral species having at least one lone pair of electrons :

For example, ammonia, amines, alcohols, etc. act as Lewis bases because they contain a pair of electrons.

$:{\mathrm{NH}}_3-\ddot{\mathrm{N}}{\mathrm{H}}_2\mathrm{R}-\ddot{0}-\mathrm{O}-\mathrm{H}$

ii. Negatively charged species or anions:

For example, chloride, cyanide, hydroxide ions, etc. act as Lewis bases.

${\mathrm{CN}}^{-},{\mathrm{Cl}}^{-},{\mathrm{OH}}^{-}$

It may be noted that all Bronsted bases are also Lewis bases but all Bronsted acids are not Lewis acids.

Limitations of Lewis concept

i. The important requirement of Lewis concept is the formation of a coordinate bond when a base reacts with an acid. However, well known acids such as $\mathrm{HCl},{\mathrm{H}}_2{\mathrm{SO}}_4$, etc., do not form coordinate bonds.

ii. The neutralisation process is usually fast but the formation of coordinate bond is slow.

Acid strength of simple cations increases with

i. Increase in +ve charge on the ion, i.e., ${\mathrm{Fe}}^{2+}<{\mathrm{Fe}}^{3+}$

ii. Adecrease in ionic radius ${\mathrm{K}}^{+}<{\mathrm{Na}}^{+}<{\mathrm{Li}}^{+}$

iii. An increase in effective nuclear charge for atoms ${\mathrm{Li}}^{+}<{\mathrm{Be}}^{2+}<{\mathrm{B}}^{3+}$

Note: The strength of cations as acids can alternatively be expressed in terms of effective nuclear charge. More is the effective nuclear charge more is the tendency to attract Ione pair of electron and thus, more is acidic nature, i.e.,

Acidic nature order : ${\mathrm{Li}}^{+}>{\mathrm{Na}}^{+}>{\mathrm{K}}^{+}$

iv. An increase in the number and relative electronegativity of the atom attached to central atom ${\mathrm{SO}}_2<{\mathrm{SO}}_3$.

v. Adecrase in atomic radius of the central atom.

However, these rules show some anomalies, e.g., acidic strength of boron trihalides is ${\mathrm{BF}}_3<{\mathrm{BCl}}_3<{\mathrm{BBr}}_3<{\mathrm{BI}}_3$.

Relative strength of acids and bases

The ratio of strengths of acids is known as relative strength, i.e.,

$\text{ Relative strength }=\frac{\text{ Strength of acid I }}{\text{ Strength of acid II }}$

For weak acids

Relative strength for weak acids can be derived as follows :

Say acid ${\mathrm{HA}}_1$ and ${\mathrm{HA}}_2$ are taken, then for,

${\mathrm{HA}}_1\rightleftharpoons {\mathrm{H}}^{+}+{\mathrm{A}}_1$

${\mathrm{K}}_{{\mathrm{a}}_1}={\mathrm{C}}_1{\alpha }_1^2$

${\mathrm{HA}}_2\rightleftharpoons {\mathrm{H}}^{+}+{\mathrm{A}}_2$

${\mathrm{K}}_{{\mathrm{a}}_2}={\mathrm{C}}_2{\alpha }_2{}^2$

If concentrations are same, then

$\text{ Relative strength }=\sqrt{\frac{{\mathrm{K}}_{\mathrm{a}1}}{{\mathrm{K}}_{\mathrm{a}2}}}$

Self Ionisation of Water

Pure water is a weak electrolyte and dissociates as :

${\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{H}}^{+}+{\mathrm{OH}}^{-}$

or $2{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{H}}_3{\mathrm{O}}^{+}+{\mathrm{OH}}^{-}$

Before dissociation $100$

After dissociation $1-\alpha \alpha \alpha$

Applying the law of equilibrium to dissociation equilibrium of water

$${\mathrm{K}}_{\mathrm{eq}}=\frac{[{\mathrm{H}}^{+}\mid {\mathrm{OH}}^{-}]}{\left[{\mathrm{H}}_2\mathrm{O}\right]}$$

where, ${\mathrm{K}}_{\mathrm{eq}}$ is dissociation constant or equilibrium constant of water.

Since, dissociation of water is too less and thus, $[{\mathrm{H}}_2\mathrm{O}$ ], i.e., the concentration of undissociated ${\mathrm{H}}_2\mathrm{O}$ can be taken as constant, therefore

$\mathrm{K}\left[{\mathrm{H}}_2\mathrm{O}\right]\rightleftharpoons \left[{\mathrm{H}}^{+}\right]+\left[{\mathrm{OH}}^{-}\right]$

or${\mathrm{K}}_{\mathrm{w}}=\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{OH}}^{-}\right]$

The new constant $K_w$ is known as ionic product constant of water. The numerical value of $K_w$ increases considerbly with temperature.

$\begin{array}{cc}\text{Temperature }\left({}^{\circ }\mathrm{C}\right)& \text{Value of }{K}_{\mathrm{w}}\\ 0& 0.11\times {10}^{-14}\\ 10& 0.31\times {10}^{-14}\\ 25& 1.00\times {10}^{-14}\\ 100& 7.50\times {10}^{-14}\end{array}$

The value of ${\mathrm{K}}_{\mathrm{w}}$ at ${25}^{\circ }\mathrm{C}$ is $1\times {10}^{-14}$. Since, pure water is neutral in nature, ${\mathrm{H}}^{+}$ion concentration must be equal to ${\mathrm{OH}}^{-}$ion concentration.

$$\begin{array}{ll}& \left[{\mathrm{H}}^{+}\right]=\left[{\mathrm{OH}}^{-}\right]=\mathrm{x}\\ \text{ or }& \left[{\mathrm{H}}^{+}\right]\left[{\mathrm{OH}}^{-}\right]={\mathrm{x}}^2=1\times {10}^{-14}\\ \text{ or }& \mathrm{x}=1\times {10}^{-7}\mathrm{M}\\ \text{ or }& \left[{\mathrm{H}}^{+}\right]=\left[{\mathrm{OH}}^{-}\right]=1\times {10}^{-7}{\mathrm{mollitre}}^{-1}\end{array}$$

pH scale

This concept was given by Sorensen in 1909.

$\mathrm{pH}$ of a solution is the negative logarithm to the base 10 of the concentration of ${\mathrm{H}}^{+}$ions which it contains

$$\begin{array}{rl}& \left[{\mathrm{H}}^{+}\right]={10}^{-\mathrm{pH}}\\ & \mathrm{pH}=-\log \left[{\mathrm{H}}^{+}\right]\\ & \mathrm{pH}=\log \frac{1}{\left[{\mathrm{H}}^{+}\right]}\end{array}$$

Just as $\mathrm{pH}$ indicates the hydrogen ion concentration, $\mathrm{pOH}$ represents the hydroxyl ion concentration $\mathrm{pOH}=-\log \left[{\mathrm{OH}}^{-}\right]$

Considering the relationship

$\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{OH}}^{-}\right]={\mathrm{K}}_w=1\times {10}^{-14}$

Taking log on both sides

$\begin{array}{rl}& \log \left[{\mathrm{H}}^{+}\right]+\log \left[{\mathrm{OH}}^{-}\right]=\log {\mathrm{K}}_{\mathrm{w}}\\ & -\log \left[{\mathrm{H}}^{+}\right]-\log \left[{\mathrm{OH}}^{-}\right]=-\log {10}^{-14}\end{array}$

or $\mathrm{pH}+\mathrm{pOH}=14$

pH scale

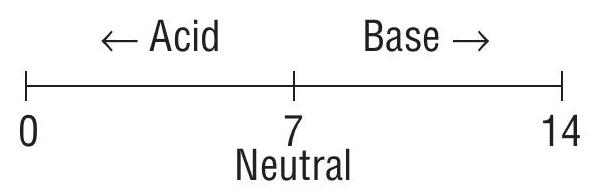
As temperature increases both $\mathrm{pH}$ and $\mathrm{pOH}$ of pure water will decrease since there will be an increase in $\left[{\mathrm{H}}^{+}\right]$and $\left[{\mathrm{OH}}^{-}\right]$due to increased dissociation.

Calculation of $\mathrm{pH}$ of weak acids

Let us consider ionization of weak monobasic acid HA; its degree of ionization is ’ $\alpha$ '

$\alpha =\frac{\mathrm{\%}\text{ ionization }}{100}$

$\mathrm{HA}\rightleftharpoons {\mathrm{H}}^{+}+{\mathrm{A}}^{-}$

Initial moles $$ C $$ 0 $$ 0

Equilibrium moles $c-c\alpha$ $c\alpha$ $c\alpha$

$\left[{\mathrm{H}}^{+}\right]=\mathrm{C}\alpha$

$\mathrm{pH}=-{\log }_{10}\left[{\mathrm{H}}^{+}\right]$

$\mathrm{pH}=-{\log }_{10}[\mathrm{c}\alpha ]$

Dissociation constant of the acid may be calculated as ;

$$\begin{array}{rl}& {\mathrm{K}}_{\mathrm{a}}=\frac{\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{A}}^{-}\right]}{[\mathrm{HA}]}=\frac{{\mathrm{C}}^2{\alpha }^2}{\mathrm{c}(1-\alpha )}\\ & =\frac{c{\alpha }^2}{(1-\alpha )}\end{array}$$

When $\alpha «<1$, it can be neglected from denominator.

${\mathrm{K}}_{\mathrm{a}}=\mathrm{c}\alpha {\alpha }^2$

$\alpha =\sqrt{\frac{K_a}{c}}$

$\left[{\mathrm{H}}^{+}\right]=\mathrm{C}\alpha =\sqrt{{\mathrm{K}}_{\alpha }\cdot \mathrm{C}}$

$\mathrm{pH}=\frac{-1}{2}\log ({\mathrm{K}}_{\alpha }\cdot \mathrm{c})$

$\mathrm{pH}=\frac{1}{2}({\mathrm{pK}}_{\mathrm{a}}-{\log }_{10}\mathrm{c})$

Calulation of $\mathrm{pH}$ of weak bases

Let us consider, the ionization of weak base in aqueous medium

$${\mathrm{NH}}_4\mathrm{OH}(\mathrm{aq})\rightleftharpoons {\mathrm{NH}}_4^{+}(\mathrm{aq})+{\mathrm{OH}}^{-}(\mathrm{aq})$$

$$ Initial moles $$ c $$ 0 $$ 0

$$ Equilibrium moles $$ $c-c\alpha c\alpha$ $c\alpha$

$\left[{\mathrm{OH}}^{-}\right]=\mathrm{c}\alpha$

$\mathrm{pOH}=-\log \left[{\mathrm{OH}}^{-}\right]$

$\mathrm{pOH}=-\log [\mathrm{c}\alpha ]$

Dissociation constant of the base may be calculated as :

$$\begin{array}{rl}& {\mathrm{K}}_{\mathrm{b}}=\frac{\left[{\mathrm{NH}}_4^{+}\right]\left[{\mathrm{OH}}^{-}\right]}{\left[{\mathrm{NH}}_4\mathrm{OH}\right]}\\ & =\frac{\mathrm{C}{\alpha }^2}{(1-\alpha )}\end{array}$$

When $\alpha «<1$, it can be neglected from denominator.

$$\begin{array}{rl}& {\mathrm{K}}_{\mathrm{b}}=\mathrm{c}{\alpha }^2\\ & \alpha =\sqrt{\frac{{\mathrm{K}}_b}{\mathrm{c}}}\end{array}$$

$$\begin{array}{rl}& \left[{\mathrm{OH}}^{-}\right]=\sqrt{{\mathrm{K}}_{\mathrm{b}}\cdot \mathrm{C}}\\ & \mathrm{pOH}=-\log {({\mathrm{K}}_{\mathrm{b}}\times \mathrm{c})}^{1/2}\\ & \mathrm{pOH}=+\frac{1}{2}\log ({\mathrm{pK}}_{\mathrm{b}}-{\log }_{10}\mathrm{C})\\ & \mathrm{pH}=14-\mathrm{pOH}\\ & \mathrm{pH}=14-\frac{1}{2}({\mathrm{pK}}_{\mathrm{b}}-{\log }_{10}\mathrm{c})\end{array}$$

Question . 1 What is the $\mathrm{pH}$ of a $0.1\mathrm{M}$ solution of acetic acid? To what volume must $500\mathrm{mL}$ of this solution be diluted so that the $\mathrm{pH}$ of the resulting solution will have twice the original value. Given ${\mathrm{K}}_{\alpha }=2.0$ $\times {10}^{-5}$

Show Answer

Answer . ${\mathrm{CH}}_3\mathrm{COOH}(\mathrm{aq})\rightleftharpoons {\mathrm{CH}}_3{\mathrm{COO}}^{-}(\mathrm{aq})+{\mathrm{H}}^{+}(\mathrm{aq})$

c

$\mathrm{c}-\mathrm{c}\alpha$

$K_a=\frac{{\left[{\mathrm{H}}^{+}\right]}^2}{\mathrm{C}-\left[{\mathrm{H}}^{+}\right]}=\frac{{\left[{\mathrm{H}}^{+}\right]}^2}{\mathrm{C}}(\because \alpha$ is small $)$

$\left[{\mathrm{H}}^{+}\right]=\sqrt{{\mathrm{K}}_{\mathrm{a}}\mathrm{C}}=1.14\times {10}^{-3}\mathrm{M}\Rightarrow \mathrm{pH}=2.85$

Also,

$c\alpha =\left[{\mathrm{H}}^{+}\right]\Rightarrow \alpha =\frac{\left[{\mathrm{H}}^{+}\right]}{\mathrm{c}}=\frac{1.14\times {10}^{-3}}{0.1}=0.014$

$\Rightarrow \mathrm{c}-\left[{\mathrm{H}}^{+}\right]\approx \mathrm{C}$

This solution is to be diluted to make $\mathrm{pH}=5.70$ (twice the original)

$\mathrm{pH}=5.7\Rightarrow \left[{\mathrm{H}}^{+}\right]=1.99\times {10}^{-6}\mathrm{M}$

Using ${\mathrm{K}}_{\alpha }=\frac{{\left[{\mathrm{H}}^{+}\right]}^2}{\mathrm{C}-\left[{\mathrm{H}}^{+}\right]}(\because \alpha$ is not small in very dilute solutions)

$\Rightarrow \mathrm{C}=\left[{\mathrm{H}}^{+}\right]+\frac{{\left[{\mathrm{H}}^{+}\right]}^2}{{\mathrm{K}}_{\alpha }}$

$=2.19\times {10}^{-6}\mathrm{M}$

Originally, the solution was $500\mathrm{mL}$ of $0.1\mathrm{M}$ solution and the concentration of new solution obtained from this solution is $2.19\times {10}^{-6}\mathrm{M}$

Using ${\mathrm{M}}_1{\mathrm{V}}_1={\mathrm{M}}_2{\mathrm{V}}_2$

$0.1\times 500=2.19\times {10}^{-6}\times V_2$

${\mathrm{V}}_2=22.83\times {10}^6\mathrm{mL}$

$=2.28\times {10}^4\mathrm{L}$

i.e. the given solution to be diluted to $2.28\times {10}^4\mathrm{L}$ so as to have $\mathrm{pH}=5.7$

Question . 2 Calculate $\mathrm{pH}$ of a solution of mixture of $10\mathrm{mL}0.1\mathrm{M}\mathrm{HCl}$ and $90\mathrm{mL}0.2\mathrm{M}\mathrm{HBr}$

Show Answer

Answer . Both $\mathrm{HCl}$ and $\mathrm{HBr}$ are strong acids and therefore we can assume complete dissociation

$\Rightarrow$ millimoles of ${\mathrm{H}}^{+}$from $\mathrm{HCl}=10\times 0.1=1$

millimoles of ${\mathrm{H}}^{+}$from $\mathrm{HBr}=90\times 0.2=18$

Total moles of ${\mathrm{H}}^{+}$in solution $=1+18=19$

Total volume of solution $=10+90=100\mathrm{mL}$

$\left[{\mathrm{H}}^{+}\right]=\frac{19}{100}=0.19\mathrm{M}$

$\mathrm{pH}=0.72$

Question . 3 Calculate the $\mathrm{pH}$ of ${10}^{-8}\mathrm{M}\mathrm{HCl}$

Show Answer

Answer . As the solution is dilute (concentration $<{10}^{-5}\mathrm{M}$ ), we will consider dissociation of water as well.

${\left[{\mathrm{H}}^{+}\right]}_{\text{coal }}={\left[{\mathrm{H}}^{+}\right]}_{\text{acid }}+{\left[{\mathrm{H}}^{+}\right]}_{\text{vater }}$

$={10}^{-8}+\mathrm{x}$

${\left[{\mathrm{OH}}^{-}\right]}_{\text{water }}={\left[{\mathrm{H}}^{+}\right]}_{\text{water }}=\mathrm{X}$

${\mathrm{K}}_w=\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{OH}}^{-}\right]$

${10}^{-14}=(\mathrm{x}+{10}^{-8})\mathrm{x}$

$\Rightarrow {\mathrm{x}}^2+{10}^{-8}\mathrm{x}-{10}^{-14}=0$

On solving the above quadratic equation

$\mathrm{x}=9.52\times {10}^{-8}\mathrm{M}$

Now

${\left[{\mathrm{H}}^{+}\right]}_{\text{ocal }}={10}^{-8}+9.52\times {10}^{-8}$

$\Rightarrow 10.05\times {10}^{-8}\Rightarrow 1.05\times {10}^{-7}$

$\mathrm{pH}=6.979$

However dilute the solution of an acid may be, it’s pH will always be less then 7 .

PRACTICE QUESTIONS

1. The conjugate acid of ${\mathrm{NH}}_2{}^{-}$is

(a) ${\mathrm{NH}}_4^{+}$

(b) ${\mathrm{NH}}_3$

(c) ${\mathrm{N}}_2{\mathrm{H}}_4$

(d) ${\mathrm{NH}}_2\mathrm{OH}$

Show Answer

Answer: (b)

2. The conjugate acid of ${\mathrm{HPO}}_4^{2-}$ is

(a) ${\mathrm{H}}_3{\mathrm{PO}}_4$

(b) ${\mathrm{PO}}_4^{3-}$

(c) ${\mathrm{H}}_2{\mathrm{PO}}_4^{-}$

(d) ${\mathrm{H}}_3{\mathrm{O}}^{+}$

Show Answer

Answer: (c)

3. Conjugate base of Hydrazoic acid $\left({\mathrm{HN}}_3\right)$ is

(a) ${\mathrm{HN}}_3^{-}$

(b) ${\mathrm{N}}^{2-}$

(c) ${\mathrm{N}}_3^{-1}$

(d) ${\mathrm{N}}^{-3}$

Show Answer

Answer: (c)

4. Which of the following can act both as a Bronsted acid and a Bronsted base?

(a) $\mathrm{HCl}$

(b)${\mathrm{H}}_3{\mathrm{PO}}_4$

(c) ${\mathrm{HCO}}_3^{-}$

(d) ${\mathrm{O}}^{2-}$

Show Answer

Answer: (c)

5. The $\mathrm{pH}$ of a solution is 5 . Its hydrogen ion concentration is increased 100 times. Its $\mathrm{pH}$ will be

(a) 7

(b) 3

(c) nearly 7

(d) does not change

Show Answer

Answer: (b)

6. An acid solution of $\mathrm{pH}=6$ is diluted 1000 times, the $\mathrm{pH}$ of the final solution becomes

(a) 6.95

(b) 6

(c) 3

(d) 9

Show Answer

Answer: (a)

7. Which of the following solution will have $\mathrm{pH}$ close to 1.0?

(a) $100\mathrm{mL}$ of M/100 HCI + $100\mathrm{mL}$ of M/10 NaOH

(b) $55\mathrm{mL}$ of $\mathrm{M}/10\mathrm{HCl}+45\mathrm{mL}$ of $\mathrm{M}/10\mathrm{NaOH}$

(c) $10\mathrm{mL}$ of $\mathrm{M}/10\mathrm{HCl}+90\mathrm{mL}$ of $\mathrm{M}/10\mathrm{NaOH}$

(d) $75\mathrm{mL}$ of $\mathrm{M}/5\mathrm{HCl}+25\mathrm{mL}$ of $\mathrm{M}/5\mathrm{NaOH}$

Show Answer

Answer: (d)

8. The $\mathrm{pH}$ of the solution produced when an aqueous solution of $\mathrm{pH}=5$ is mixed with equal volume of an aqueous solution of $\mathrm{pH}=3$ is

(a) $3.3$

(b) $4.5$

(c) $3.5$

(d) $4.0$

Show Answer

Answer: (a)

9. A monoprotic acid ( $\mathrm{HA})$ is $1$ ionised in its aqueous solution of $0.1\mathrm{M}$ strength. Its $\mathrm{pOH}$ will be

(a) 11

(b)3

(c) 10

(d) 2

Show Answer

Answer: (a)

10. The number of ${\mathrm{H}}^{+}$ions present in $1\mathrm{mL}$ of a solution having $\mathrm{pH}=13$ is

(a) ${10}^{13}$

(b)$6.022\times {10}^{13}$

(c) $6.022\times {10}^7$

(d) $6.022\times {10}^{10}$

Show Answer

Answer: (c)

11. The ${\mathrm{pK}}_{\mathrm{a}}$ of $0.1\mathrm{M}$ acetic acid solution is 4.78. The $\mathrm{pH}$ of the solution will be

(a) 1.89

(b) 2.89

(c) 4.89

(d) 2.19

Show Answer

Answer: (b)

12. $1{\mathrm{cm}}^3$ of $0.01\mathrm{N}\mathrm{HCl}$ is added to one litre of sodium chloride solution. The $\mathrm{pH}$ of the resulting solution will be

(a) 2

(b) 7

(c) 5

(d) 12

Show Answer

Answer: (c)

13. A $50\mathrm{mL}$ solution of $\mathrm{pH}=1$ is mixed with a $50\mathrm{mL}$ solution of $\mathrm{pH}=2$. The $\mathrm{pH}$ of the mixture will be nearly

(a) 0.76

(b)1.26

(c) 1.76

(d) 2.26

Show Answer

Answer: (b)

14. The $\mathrm{pH}$ of a solution obtained by mixing $50\mathrm{mL}$ of $0.4\mathrm{N}\mathrm{HCl}$ and $50\mathrm{mL}$ of $0.2\mathrm{N}\mathrm{NaOH}$ is

(a) $-\log 2$

(b) $-\log 0.2$

(c) $1.0$

(d) $2.0$

Show Answer

Answer: (c)

15. By adding $20\mathrm{mL}$ of $0.1\mathrm{N}\mathrm{HCl}$ to $20\mathrm{mL}$ of $0.001\mathrm{N}\mathrm{KOH}$, the $\mathrm{pH}$ of the solution obtained will be

(a) 2

(b)1.3

(c) 0

(d)7

Show Answer

Answer: (b)

16. The $\mathrm{pH}$ of $1.0\mathrm{M}$ aqueous solution of a weak acid $\mathrm{HA}$ is 6.0 . Its dissociation constant is

(a) $1.0\times {10}^{-12}$

(b) $1.0\times {10}^{-6}$

(c) $1.0$

(d) $6.0$

Show Answer

Answer: (a)

HYDROLYSIS OF SALTS

Determination of pH due to Hydrolysis of Salts

The phenomenon of interaction of cations and / or anions of the salt with ${\mathrm{H}}^{+}$and ${\mathrm{OH}}^{-}$ions furnished by water is called hydrolysis of a salt.

There are four categories of salts

(i) Salt of a strong acid and a strong base.

Examples

$\mathrm{NaCl},{\mathrm{K}}_2{\mathrm{SO}}_4,{\mathrm{NaNO}}_3$, $\mathrm{NaBr}$ etc.

(ii) Salt of a strong base and a weak acid.

Examples

${\mathrm{CH}}_3\mathrm{COONa},\mathrm{NaCN},{\mathrm{NaHCO}}_3,{\mathrm{Na}}_2{\mathrm{CO}}_3$ etc.

(iii) Salt of a strong acid and a weak base.

Examples

${\mathrm{FeCl}}_3,{\mathrm{CuCl}}_2,{\mathrm{AlCl}}_3,{\mathrm{NH}}_4\mathrm{Cl},{\mathrm{CuSO}}_4$ etc.

(iv) Salt of a weak acid and a weak base.

Examples

${\mathrm{CH}}_3{\mathrm{COONH}}_4,{\left({\mathrm{NH}}_4\right)}_2{\mathrm{CO}}_3,{\mathrm{NH}}_4{\mathrm{HCO}}_3$ etc.

Salts of strong acid and strong base do not undergo hydrolysis. They simply ionise and fail to change the ${\mathrm{H}}^{+}$ion concentration of solution and hence the $\mathrm{pH}$ of the solution remains 7 at ${25}^{\circ }\mathrm{C}$.

Salts of weak acid and strong base

Such salts give alkaline solution in water.

(i) Hydrolysis constant

Representing the salt by BA, the hydrolysis may be represented as follows :

or ${\mathrm{B}}^{+}+{\mathrm{A}}^{-}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{B}}^{+}+{\mathrm{OH}}^{-}+\mathrm{HA}$ ( ${\mathrm{B}}^{+}$remains in ionic state in water)

or ${\mathrm{A}}^{-}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{OH}}^{-}+\mathrm{HA}$

i.e. it is a case of anion hydrolysis.

The hydrolysis constant ${\mathrm{K}}_{\mathrm{h}}$ for the above reaction will be given by

$$\begin{array}{}\text{(i)}& {\mathrm{K}}_{\mathrm{h}}=\frac{\left[{\mathrm{OH}}^{-}\right][\mathrm{HA}]}{\left[{\mathrm{A}}^{-}\right]}\end{array}$$

For the weak acid $\mathrm{HA}$, the dissociation equilibrium is

$$\mathrm{HA}\rightleftharpoons {\mathrm{H}}^{+}+{\mathrm{A}}^{-}$$

The dissociation constant ${\mathrm{K}}_{\mathrm{a}}$ of the acid $\mathrm{HA}$ will be given by

$$\begin{array}{}\text{(ii)}& {\mathrm{K}}_{\mathrm{a}}=\frac{\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{A}}^{-}\right]}{[\mathrm{HA}]}\end{array}$$

Further the ionic product of water ${\mathrm{K}}_{\mathrm{w}}$ is given by

$$\begin{array}{}\text{(iii)}& {\mathrm{K}}_{\mathrm{w}}=\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{OH}}^{-}\right]\end{array}$$

Multiplying equation (i) with (ii) and dividing by (iii), we get

$$\frac{{\mathrm{K}}_{\mathrm{n}}{\mathrm{K}}_{\mathrm{a}}}{{\mathrm{K}}_w}=\frac{\left[{\mathrm{OH}}^{-}\right][\mathrm{HA}]}{\left[{\mathrm{A}}^{-}\right]}\times \frac{\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{A}}^{-}\right]}{[\mathrm{HA}]}\times \frac{1}{\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{OH}}^{-}\right]}$$

$$\frac{{\mathrm{K}}_{\mathrm{h}}{\mathrm{K}}_{\mathrm{a}}}{{\mathrm{K}}_{\mathrm{w}}}=1$$

or

$$\begin{array}{}\text{(iv)}& {\mathrm{K}}_{\mathrm{h}}=\frac{{\mathrm{K}}_{\mathrm{w}}}{{\mathrm{K}}_{\mathrm{a}}}\end{array}$$

(ii) Degree of Hydrolysis

Suppose the original concentration of the salt in the solution is $\mathrm{c}$ moles/litre and $\mathrm{h}$ is its degree of hydrolysis at this concentration. Then we have

Original molar conc.

$${\mathrm{A}}^{-}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{OH}}^{-}+\mathrm{HA}$$

Molar conc. at equilibrium

c $00$

The hydrolysis constant $\left({\mathrm{K}}_{\mathrm{h}}\right)$ will, therefore, be given by

${\mathrm{K}}_{\mathrm{h}}=\frac{\left[{\mathrm{OH}}^{-}\right][\mathrm{HA}]}{\left[{\mathrm{A}}^{-}\right]}=\frac{\mathrm{ch}.\mathrm{ch}}{\mathrm{c}(1-\mathrm{h})}=\frac{{\mathrm{ch}}^2}{1-\mathrm{h}}$

If $h$ is very small as compared to 1 , we can take $1-h=1$ so that the above expression becomes

${\mathrm{ch}}^2={\mathrm{K}}_{\mathrm{h}}$ or ${\mathrm{h}}^2=\frac{{\mathrm{K}}_{\mathrm{h}}}{\mathrm{c}}$ or $\mathrm{h}=\sqrt{\frac{{\mathrm{K}}_{\mathrm{h}}}{\mathrm{c}}}$

Substituting the value of ${\mathrm{K}}_{\mathrm{a}}$ from equation (iv), we get

$$\begin{array}{}\text{(v)}& h=\sqrt{\frac{{\mathrm{K}}_{\mathrm{w}}}{{\mathrm{K}}_{\mathrm{a}}\mathrm{C}}}\end{array}$$

(iii) $\mathbf{p}\mathbf{H}$

(In the present case, we have)

Original conc.

$${\mathrm{A}}^{-}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{OH}}^{-}+\mathrm{HA}$$

conc. at equilibrium

C

$00$

i.e., $\left[{\mathrm{OH}}^{-}\right]=\mathrm{ch}$

$\left[{\mathrm{H}}^{+}\right]=\frac{{\mathrm{K}}_{\mathrm{w}}}{\left[{\mathrm{OH}}^{-}\right]}=\frac{{\mathrm{K}}_{\mathrm{w}}}{\mathrm{ch}}$

Substituting the value of ’ $h$ ’ from equation ( $v$ ), we get

$\left[{\mathrm{H}}^{+}\right]=\frac{{\mathrm{K}}_{\mathrm{w}}}{\mathrm{C}}=\sqrt{\frac{{\mathrm{K}}_{\mathrm{a}}\mathrm{C}}{{\mathrm{K}}_{\mathrm{w}}}}$

or $\begin{array}{rl}& \left[{\mathrm{H}}^{+}\right]=\sqrt{\frac{K_w{K}_a}{c}}\\ & pH=-\log \left[H^{+}\right]=-\log \sqrt{\frac{K_w{K}_a}{C}}=-\log {\left(\frac{K_w{K}_a}{C}\right)}^{1/2}\end{array}$

or $\mathrm{pH}=-\frac{1}{2}[\log {\mathrm{K}}_w+\log {\mathrm{K}}_{\mathrm{a}}-\log \mathrm{c}]=\frac{1}{2}[{\mathrm{pK}}_w+{\mathrm{pK}}_{\mathrm{a}}-\log \mathrm{c}]$

Thus knowing the molar concentration ’ $c$ ’ of the solution and the dissociation constant ’ ${\mathrm{K}}_{\mathrm{a}}$ ’ of the weak acid involved, the $\mathrm{pH}$ of the solution can be calculated.

2. Salts of strong acid and weak base

(I). Hydrolysis constant

For the salt BA, the hydrolysis may be represented as :

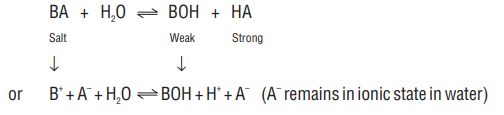
or ${\mathrm{B}}^{+}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons \mathrm{BOH}+{\mathrm{H}}^{+}$

i.e. it is a case of cation hydrolysis.

The hydrolysis constant ${\mathrm{K}}_{\mathrm{h}}$ will be given by

$$\begin{array}{}\text{(vii)}& {\mathrm{K}}_{\mathrm{h}}=\frac{[\mathrm{BOH}]\left[{\mathrm{H}}^{+}\right]}{\left[{\mathrm{B}}^{+}\right]}\end{array}$$

For the weak base $\mathrm{BOH}$, the dissociation equilibrium is

$$\mathrm{BOH}\rightleftharpoons {\mathrm{B}}^{+}+{\mathrm{OH}}^{-}$$

The dissociation constant ${\mathrm{K}}_b$ of the weak base $\mathrm{BOH}$ will be given by

$$\begin{array}{}\text{(viii)}& {\mathrm{K}}_{\mathrm{b}}=\frac{\left[{\mathrm{B}}^{+}\right]\left[{\mathrm{OH}}^{-}\right]}{[\mathrm{BOH}]}\end{array}$$

The ionic product of water ${\mathrm{K}}_w$ is given by

$$\begin{array}{}\text{(ix)}& {\mathrm{K}}_{\mathrm{w}}=\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{OH}}^{-}\right]\end{array}$$

Multiplying equation (vii) with (viii) and dividing by (ix), we get

$$\begin{array}{}\text{(x)}& \frac{{\mathrm{K}}_{\mathrm{h}}{\mathrm{K}}_{\mathrm{b}}}{{\mathrm{K}}_{\mathrm{w}}}=1\text{ or }{\mathrm{K}}_{\mathrm{h}}=\frac{{\mathrm{K}}_{\mathrm{w}}}{{\mathrm{K}}_{\mathrm{b}}}\end{array}$$

(ii) Degree of Hydrolysis

Proceeding as in the earlier case, we get the same relationship viz.

$$\mathrm{h}=\sqrt{\frac{{\mathrm{K}}_{\mathrm{h}}}{\mathrm{c}}}$$

Substituting the value of ${\mathrm{K}}_{\mathrm{h}}$ from equation ( $\mathrm{x}$ ), we get

$$\begin{array}{}\text{(xi)}& h=\sqrt{\frac{{\mathrm{K}}_{\mathrm{w}}}{{\mathrm{K}}_{\mathrm{b}}\mathrm{C}}}\end{array}$$

(iii) $\mathrm{pH}$

(In this case, we have)

$\begin{array}{llll}& {\mathrm{B}}^{+}+{\mathrm{H}}_2\mathrm{O}& \rightleftharpoons & \mathrm{BOH}+{\mathrm{H}}^{+}\\ \text{Original conc. }& \mathrm{c}& & 0& 0\\ \text{ conc. at equilibrium }& \mathrm{c}(1-\mathrm{h})& & \text{ ch }\text{ ch }\\ \Rightarrow \left[{\mathrm{H}}^{+}\right]=\mathrm{ch}& & & & \end{array}$

Substituting the value of ’ $h$ ’ from equation (xi), we get

$$\begin{array}{rl}& \left[H^{+}\right]=c\cdot \sqrt{\frac{K_w}{K_b\cdot C}}=\sqrt{\frac{K_w\cdot C}{K_b}}={\left(\frac{K_w\cdot C}{K_b}\right)}^{1/2}\\ & pH=-\log \left[H^{+}\right]=-\log {\left(\frac{K_w\cdot C}{K_b}\right)}^{1/2}\end{array}$$

or $\mathrm{pH}=-\frac{1}{2}[\log {\mathrm{K}}_w-\log {\mathrm{K}}_{\mathrm{b}}+\log \mathrm{c}]=\frac{1}{2}[{\mathrm{pK}}_w-{\mathrm{pK}}_{\mathrm{b}}-\log \mathrm{c}]$

3. Salts of weak acid and weak base

(i) Hydrolysis constant

Representing the salt by $BA$ we have

$$\begin{array}{rl}& \mathrm{BA}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons \mathrm{BOH}+\mathrm{HA}\\ & \text{ Salt }\text{ Weak Weak }\end{array}$$

or ${\mathrm{B}}^{+}+{\mathrm{A}}^{-}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons \mathrm{BOH}+\mathrm{HA}$

i.e. it involves both anion hydrolysis as well as cation hydrolysis. Writing the various equation as before, we have

$$\begin{array}{}\text{(xiii)}& {\mathrm{K}}_{\mathrm{n}}=\frac{[\mathrm{BOH}][\mathrm{HA}]}{\left[{\mathrm{B}}^{+}\right]\left[{\mathrm{A}}^{-}\right]}\end{array}$$

For the weak acid, $HA\rightleftharpoons H^{+}+A^{-}$, so that $K_a=\frac{\left[H^{+}\right]\left[A^{-}\right]}{[HA]}$

For the weak base, $\mathrm{BOH}\rightleftharpoons {\mathrm{B}}^{+}+{\mathrm{OH}}^{-}$, so that ${\mathrm{K}}_{\mathrm{b}}=\frac{\left[{\mathrm{B}}^{+}\right]\left[{\mathrm{OH}}^{-}\right]}{[\mathrm{BOH}]}$

Also, we know that ${\mathrm{K}}_{\mathrm{w}}=\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{OH}}^{-}\right]$

Multiplying equation (iii), (xiv), (xv) and dividing by equation (xvi), we get

$$\begin{array}{}\text{(xvii)}& \frac{K_h\cdot K_a\cdot K_b}{K_w}=1\text{ or }{K}_n=\frac{K_w}{K_a{K}_b}\end{array}$$

(ii) Degree of hydrolysis.

In this case, we have

${\mathrm{B}}^{+}+{\mathrm{A}}^{-}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons \mathrm{BOH}+\mathrm{HA}$

Original conc. $CC00$

Molar conc. at equilibrium $C(1-h)C(1-h)ChCh$

$$\begin{array}{}\text{(xviii)}& K_h=\frac{[BOH][HA]}{\left[B^{+}\right]\left[A^{-}\right]}=\frac{ch\cdot ch}{c(1-h)c(1-h)}=\frac{h^2}{(1-h{)}^2}\end{array}$$

Here, the relationship between ’ $K_h$ ’ and ’ $h$ ’ does not involve ’ $c$ ‘. Thus the degree of hydrolysis of such a salt is independent of the concentration of the solution.

If ’ $h$ ’ is very small in comparison to 1 , we can take $1-h\cong 1$ so that equation (xviii) becomes

$$\begin{array}{}\text{(xix)}& K_h=h^2\text{ or }h=\sqrt{K_h}\text{ or }{K}_h=\sqrt{\frac{K_w}{K_a{K}_b}}\end{array}$$

(iii) $\mathrm{pH}$

for the weak acid $\mathrm{HA}$.

$$\begin{array}{rl}& \mathrm{HA}\rightleftharpoons {\mathrm{H}}^{+}+{\mathrm{A}}^{-}\\ & {\mathrm{K}}_{\mathrm{a}}=\frac{\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{A}}^{-}\right]}{[\mathrm{HA}]}\\ & \left[{\mathrm{H}}^{+}\right]=\frac{{\mathrm{K}}_{\mathrm{a}}[\mathrm{HA}]}{\left[{\mathrm{A}}^{-}\right]}={\mathrm{K}}_{\mathrm{a}}\frac{\mathrm{ch}}{\mathrm{c}(1-\mathrm{h})}={\mathrm{K}}_{\mathrm{a}}\frac{\mathrm{h}}{1-\mathrm{h}}\end{array}$$

Butfrom equation (xviii), $\frac{\mathrm{h}}{1-\mathrm{h}}=\sqrt{{\mathrm{K}}_{\mathrm{h}}}$ so that we have

$$\begin{array}{rlr}& \left[H^{+}\right]=K_a\sqrt{K_h}=K_a\sqrt{\frac{K_w}{K_a{K}_b}}=\sqrt{\frac{K_a{K}_w}{K_b}}& pH=-\log \left[H^{+}\right]=-\log \sqrt{\frac{K_a{K}_w}{K_b}}=-\log {\left(\frac{K_a{K}_w}{K_b}\right)}^{1/2}\end{array}$$

or $\mathrm{pH}=-\frac{1}{2}[\log {\mathrm{K}}_{\mathrm{a}}+\log {\mathrm{K}}_{\mathrm{w}}-\log {\mathrm{K}}_b]=\frac{1}{2}[{\mathrm{pK}}_{\mathrm{w}}+{\mathrm{pK}}_{\mathrm{a}}-{\mathrm{pK}}_b]$

The degree of hydrolysis and $\mathrm{pH}$ of salts made up of weak acid and weak base is independent of concentration of salt. The above equation is applicable even when ’ $h$ ’ is large as no approximation of ‘h’ comparison with unity has been taken in the derivation.

Note:

Degree of hydrolysis always increases with increase in temperature as because at elevated temperature the increase in ${\mathrm{K}}_w$ is greater as compared to ${\mathrm{K}}_a$ & ${\mathrm{K}}_b$.

Weaker is the acid or base, greater is the hydrolysis constant.

Degree of hydrolysis increases when ’ $c$ ’ decreases i.e. with dilution.

For any acid and its conjugate base or vice-versa ${\mathrm{pK}}_{\mathrm{a}}+{\mathrm{pk}}_{\mathrm{b}}={\mathrm{pK}}_{\mathrm{w}}$.

Question . 4 At ${25}^{\circ }\mathrm{C},5\mathrm{mL}$ of $0.4\mathrm{M}$ weak mono acidic base is titrated with $0.2\mathrm{M}\mathrm{HCl}$ solution. What is the concentration of ${\mathrm{H}}^{+}$ions at equivalence point. Given ${\mathrm{K}}_{\mathrm{b}}=1.0\times {10}^{-12},{\mathrm{K}}_{\mathrm{w}}=1\times {10}^{-14}$.

Show Answer

Answer . Volume of acid required to reach the equivalence point.

$\begin{array}{rl}& \text{ meq of Base }=\text{ meq of }\mathrm{HCl}\\ \Rightarrow & 5\times (0.4\times 1)=(0.2\times 1)V_{\mathrm{HCl}}\\ & V_{\mathrm{HCl}}=\frac{5\times 0.4}{0.2}=10\mathrm{mL}\end{array}$

$\Rightarrow$ The net volume of solution at equivalence point is $5\mathrm{mL}+10\mathrm{mL}=15\mathrm{mL}$

Concentration of salt $=\frac{5\times 0.4}{15}=0.13\mathrm{M}$

The salt so formed is a combination of weak base and strong acid

$\therefore$ Cation will undergo hydrolysis

$\begin{array}{rl}& {\mathrm{B}}^{+}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons \mathrm{BOH}+{\mathrm{H}}^{+}\\ & \mathrm{c}-\mathrm{ch}\text{ ch }\mathrm{ch}\end{array}$

${\mathrm{K}}_{\mathrm{h}}=\frac{[\mathrm{BOH}]\left[{\mathrm{H}}^{+}\right]}{\left[{\mathrm{B}}^{+}\right]}=\frac{{\mathrm{C}}^2{\mathrm{h}}^2}{\mathrm{c}(1-\mathrm{h})}$

Also $K_b=\frac{K_w}{K_h}={10}^{-2}=\frac{{\left[{\mathrm{H}}^{+}\right]}^2}{c-\left[{\mathrm{H}}^{+}\right]}$

${\left[{\mathrm{H}}^{+}\right]}^2={10}^{-12}\mathrm{C}-{10}^{-2}\left[{\mathrm{H}}^{+}\right]$

or ${\left[{\mathrm{H}}^{+}\right]}^2+{10}^{-2}\left[{\mathrm{H}}^{+}\right]-{10}^{-2}\mathrm{C}=0$

$\left[{\mathrm{H}}^{+}\right]=\frac{-{10}^{-2}\pm \sqrt{{10}^{-4}+4\times 0.13\times {10}^{-2}}}{2}$

$=3.64\times {10}^{-2}\mathrm{M}$

Question . 5 Equal volume of two solution having $\mathrm{pH}=2$ and $\mathrm{pH}=10$ are mixed together at ${90}^{\circ }\mathrm{C}$. What is the $\mathrm{pH}$ of the resulting solution $({\mathrm{K}}_{\mathrm{w}}={10}^{-12})$ at ${90}^{\circ }\mathrm{C}$.

Show Answer

Answer . Given

$$\begin{array}{rl}& {\mathrm{K}}_{\mathrm{w}}={10}^{-12}\text{ at }{90}^{\circ }\mathrm{C}\\ & {\mathrm{K}}_{\mathrm{w}}=\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{OH}}^{-}\right]={10}^{-12}\\ & \Rightarrow \left[{\mathrm{H}}^{+}\right]=\left[{\mathrm{OH}}^{-}\right]={10}^{-6}\\ & \mathrm{pH}=2\Rightarrow \left[{\mathrm{H}}^{+}\right]={10}^{-2}\mathrm{M}\\ & \text{ pH }=10\Rightarrow \mathrm{p}\left[{\mathrm{OH}}^{-}\right]=12-10=2\\ & \text{ or }\left[{\mathrm{OH}}^{-}\right]={10}^{-2}\mathrm{M}\end{array}$$

Addition of equal volumes of acid and base results in the formation of neutral solution. The $\mathrm{pH}$ of this neutral solution is 6 at ${90}^{\circ }\mathrm{C}$.

PRACTICE QUESTIONS

1. The dissociation constant of ${\mathrm{CH}}_3\mathrm{COOH}$ is $1.8\times {10}^{-5}$. The hydrolysis constant for $0.1\mathrm{M}$ sodium acetate is

(a) $5.56\times {10}^4$

(b) $5.56\times {10}^{-10}$

(c) $1.8\times {10}^{-5}$

(d) $1.8\times {10}^9$

Show Answer

Answer: (b)

2. $\mathrm{pH}$ of $2\mathrm{M}\mathrm{NaCl}$ will be

(a) 3

(b)6.5

(c) 7

(d) 10

Show Answer

Answer: (c)

3. Dissociation constant of ${\mathrm{NH}}_4\mathrm{OH}$ is $1.8\times {10}^{-5}$. The hydrolysis constant of ${\mathrm{NH}}_4\mathrm{Cl}$ would be

(a) $1.80\times {10}^{-19}$

(b) $5.55\times {10}^{-10}$

(c) $5.55\times {10}^{-5}$

(d) $1.80\times {10}^{-5}$

Show Answer

Answer: (b)

4. If ${\mathrm{pK}}_b$ for fluoride ion at ${25}^{\circ }\mathrm{C}$ is 10.83 , the ionization constant of $\mathrm{HF}$ in water at this temperature is

(a) $1.74\times {10}^{-5}$

(b) $3.52\times {10}^{-3}$

(c) $6.75\times {10}^{-4}$

(d) $5.38\times {10}^{-2}$

Show Answer

Answer: (c)

5. An aqueous solution of carbonic acid $\left({\mathrm{H}}_2{\mathrm{CO}}_3\right)$ contains

(a) ${\mathrm{H}}_2{\mathrm{CO}}_3$ only

(b) ${\mathrm{H}}_2{\mathrm{CO}}_3,{\mathrm{H}}^{+},{\mathrm{HCO}}_3^{-}$

(c) ${\mathrm{H}}_2{\mathrm{CO}}_3,{\mathrm{H}}^{+},{\mathrm{HCO}}_3^{-},{\mathrm{CO}}_3^{2-}$

(d) ${\mathrm{H}}_2{\mathrm{CO}}_3,{\mathrm{CO}}_2,{\mathrm{H}}^{+},{\mathrm{HCO}}_3^{-},{\mathrm{CO}}_3{}^{2-}$

Show Answer

Answer: (d)

6. The $\mathrm{pH}$ of $0.1\mathrm{M}$ solution of the following salts increases in the order

(a) $\mathrm{NaCl}<{\mathrm{NH}}_4\mathrm{Cl}<\mathrm{NaCN}<\mathrm{HCl}$

(b) $\mathrm{HCl}<{\mathrm{NH}}_4\mathrm{Cl}<\mathrm{NaCl}<\mathrm{NaCN}$

(c) $\mathrm{NaCN}<{\mathrm{NH}}_4\mathrm{Cl}<\mathrm{NaCl}<\mathrm{HCl}$

(d) $\mathrm{HCl}<\mathrm{NaCl}<\mathrm{NaCN}<{\mathrm{NH}}_4\mathrm{Cl}$

Show Answer

Answer: (b)

7. Which of the following salt solutions ( $0.1\mathrm{M}$ each) will have the lowest $\mathrm{pH}$ values?

(a) ${\mathrm{CaCO}}_3$

(b) ${\mathrm{CaCl}}_2$

(c) $\mathrm{Ca}(\mathrm{OH}{)}_2$

(d) ${\mathrm{CH}}_3\mathrm{COONa}$

Show Answer

Answer: (b)

8. A weak acid ${\mathrm{HX}}^2$ has ${\mathrm{pK}}_{\mathrm{a}}=5$. The percent degree of hydrolysis of $0.1\mathrm{M}$ solution of salt $\mathrm{NaX}$ is

(a) $0.001$

(b)$0.01$

(c) $0.1$

(d)$0.15$

Show Answer

Answer: (b)

9. $2.5\mathrm{mL}$ of $(2/5)\mathrm{M}$ weak monoacidic base $({\mathrm{K}}_{\mathrm{b}}=1\times {10}^{-12}$ at ${25}^{\circ }\mathrm{C})$ is titrated with $(2/15)\mathrm{M}\mathrm{HCl}$ in water at ${25}^{\circ }\mathrm{C}$. The concentration of ${\mathrm{H}}^{+}$at equivalence point is $({\mathrm{K}}_w=1\times {10}^{-14}$ at ${25}^{\circ }\mathrm{C})$

(a) $3.7\times {10}^{-13}\mathrm{M}$

(b)$3.2\times {10}^{-7}\mathrm{M}$

(c) $3.2\times {10}^{-2}\mathrm{M}$

(d)$2.7\times {10}^{-2}\mathrm{M}$

Show Answer

Answer: (d)

10. What is the percentage hydrolysis of $\mathrm{NaCN}$ in $\mathrm{N}/80$ solution when the dissociation constant for HCN is $1.3\times {10}^{-9}$ and ${\mathrm{K}}_w=1.0\times {10}^{-14}$.

(a) 2.48

(b)5.26

(c) 8.2

(d)9.6

Show Answer

Answer: (a)

11. The $\mathrm{pH}$ of a $1{\mathrm{MCH}}_3\mathrm{COONa}$ solution in water will be nearly

(a) 2.4

(b)5.4

(c) 7.4

(d)9.4

Show Answer

Answer: (d)

12. Ammonium cyanide is a salt of ${\mathrm{NH}}_4\mathrm{OH}({\mathrm{K}}_b=1.8\times {10}^{-5})$ and $\mathrm{HCN}({\mathrm{K}}_{\mathrm{a}}=4.0\times {10}^{-10})$. The hydrolysis constant of $0.1\mathrm{M}{\mathrm{NH}}_4\mathrm{CN}$ at ${25}^{\circ }\mathrm{C}$ is

(a) $1.4$

(b)$7.2\times {10}^{-15}$

(c) $7.2\times {10}^{-1}$

(d) $1.4\times {10}^{-6}$

Show Answer

Answer: (a)

13. It is found that $0.1\mathrm{M}$ solution of three salts $\mathrm{NaX},\mathrm{NaY}$ and $\mathrm{NaZ}$ have $\mathrm{pH}$ values $7.0,9.0$ and 11.0 respectively. Which of the following order regarding acid strength is correct?

(a) $\mathrm{HX}>\mathrm{HY}>\mathrm{HZ}$

(b) $\mathrm{HX}>\mathrm{HZ}>\mathrm{HY}$

(c) $\mathrm{HY}>\mathrm{HX}>\mathrm{HZ}$

(d) $\mathrm{HZ}>\mathrm{HY}>\mathrm{HX}$

Show Answer

Answer: (a)

14. The degree of hydrolysis of ammonium acetate is related to its hydrolysis constant by the expression

(a) $\alpha =\frac{{\mathrm{K}}_{\mathrm{h}}}{1+{\mathrm{K}}_{\mathrm{h}}}$

(b) $\alpha =\frac{K_n}{1+K_n^2}$

(c) $\alpha =\frac{\sqrt{{\mathrm{K}}_{\mathrm{h}}}}{1+\sqrt{{\mathrm{K}}_{\mathrm{h}}}}$

(d) $\alpha =\frac{\sqrt{K_h}}{1-\sqrt{K_h}}$

Show Answer

Answer: (c)

15. The hydrolysis constant of anilinium acetate at ${25}^{\circ }\mathrm{C}$ is $({\mathrm{K}}_{\mathrm{a}}\left({\mathrm{CH}}_3\mathrm{COOH}\right)=1.8\times {10}^{-5}\mathrm{M}$ and ${\mathrm{K}}_{\mathrm{b}}$ (aniline) $=4.6\times {10}^{-10}\mathrm{M}$ )

(a) 1.0

(b)1.21

(c) 1.35

(d) $2.6\times {10}^{-2}$

Show Answer

Answer: (b)

16. The expression to compute pH of a solution containing a salt formed from a weak acid and a weak base is

(a) $\mathrm{pH}=\frac{1}{2}({\mathrm{pK}}_{\mathrm{w}}+{\mathrm{pK}}_{\mathrm{b}}-{\mathrm{pK}}_{\mathrm{a}})$

(b) $\mathrm{pH}=\frac{1}{2}({\mathrm{pK}}_{\mathrm{w}}+{\mathrm{pK}}_{\mathrm{a}}-{\mathrm{pK}}_{\mathrm{b}})$

(c) $\mathrm{pH}=\frac{1}{2}({\mathrm{pK}}_{\mathrm{a}}-{\mathrm{pK}}_{\mathrm{b}})+\log ([$ salt $]/\mathrm{c})$

(d) $\mathrm{pH}=\frac{1}{2}({\mathrm{pK}}_{\mathrm{a}}+{\mathrm{pK}}_{\mathrm{b}})-\log ([$ salt $]/\mathrm{c})$

Show Answer

Answer: (b)

17. The $\mathrm{pH}$ of $0.1\mathrm{M}$ solution of ${\mathrm{NaHCO}}_3$ is (Given: ${\mathrm{pK}}_{\mathrm{a}}\left({\mathrm{H}}_2{\mathrm{CO}}_3\right)=6.38$ and ${\mathrm{pK}}_{\mathrm{a}2}\left({\mathrm{HCO}}_3^{-}\right)=10.32$ )

(a) $8.35$

(b)6.5

(c) 4.3

(d) 3.94

Show Answer

Answer: (a)

BUFFER SOULTIONS

A solution whose $\mathrm{pH}$ is not altered to any great extent by the addition of small quantities, of either an acid ( ${\mathrm{H}}^{+}$ions) or a base $({\mathrm{OH}}^{-}$ions) is called a buffer solution.

General Characteristics of a Buffer Solution

(i) It has a definite $\mathrm{pH}$, i.e. it has reserve acidity or alkalinity.

(ii) Its $\mathrm{pH}$ does not change on standing for long.

(iii) Its pH does not change on dilution.

Buffer solutions can be obtained

(i) by mixing a weak acid with its salt with a strong base, e.g.,

(a) ${\mathrm{CH}}_3\mathrm{COOH}+{\mathrm{CH}}_3\mathrm{COONa}$

(b) Boric acid + Borax

(c) Phthalic acid + Potassium phthalate

(ii) by mixing a weak base with its salt with strong acid, e.g.,

(a) ${\mathrm{NH}}_4\mathrm{OH}+{\mathrm{NH}}_4\mathrm{Cl}$

(b) Glycine + Glycine hydrochloride

(iii) by a solution of ampholyte. The ampholytes or amphoteric electrolytes are the substances which show properties of both an acid and a base. Proteins and amino acids are the examples of such electrolytes.

(iv) by a mixture of an acid salt and a normal salt of a polybasic acid, e.g., ${\mathrm{Na}}_2{\mathrm{HPO}}_4+{\mathrm{Na}}_3{\mathrm{PO}}_4$, or a salt of a weak acid and a weak base, such as ${\mathrm{CH}}_3{\mathrm{COONH}}_4$.

Types of Buffers

(i) Acidic buffer : A weak acid with its conjugate base :

${\mathrm{NaHCO}}_3+{\mathrm{H}}_2{\mathrm{CO}}_3({\mathrm{H}}_2{\mathrm{CO}}_3$ : is weak acid and ${\mathrm{HCO}}_3^{-}$is its conjugate base;

${\mathrm{CH}}_3\mathrm{COOH}+{\mathrm{CH}}_3\mathrm{COONa}$;

Boric acid + Borax;

${\mathrm{CH}}_3\mathrm{COOH}+{\mathrm{CH}}_3{\mathrm{COONH}}_4$;

Phthalic acid + Potassium phthalate;

${\mathrm{NaH}}_2{\mathrm{PO}}_4+{\mathrm{H}}_3{\mathrm{PO}}_4$ and a mixture of an acid salt and normal salt of a polybasic acid, e.g., ${\mathrm{Na}}_2{\mathrm{HPO}}_4+{\mathrm{Na}}_3{\mathrm{PO}}_4$.

Explanation of Buffer Action

Acidic buffer : Consider the case of the solution of acetic acid containing sodium acetate. Acetic acid is feebly ionised while sodium acetate is almost completely ionised. The mixture thus contains ${\mathrm{CH}}_3\mathrm{COOH}$ molecules, ${\mathrm{CH}}_3{\mathrm{COO}}^{-}$ions, ${\mathrm{Na}}^{+}$ions, ${\mathrm{H}}^{+}$ions and ${\mathrm{OH}}^{-}$ions. Thus we have the following equilibria in solution :

$$\begin{array}{rl}& {\mathrm{CH}}_3\mathrm{COOH}\rightleftharpoons {\mathrm{H}}^{+}+{\mathrm{CH}}_3{\mathrm{COO}}^{-}(\text{Feebly ionised })\\ & {\mathrm{CH}}_3\mathrm{COONa}\rightleftharpoons {\mathrm{Na}}^{+}+{\mathrm{CH}}_3{\mathrm{COO}}^{-}\text{(Completely ionised })\end{array}$$

When a drop of strong acid, say $\mathrm{HCl}$, is added, the ${\mathrm{H}}^{+}$ions furnished by $\mathrm{HCl}$ combine with ${\mathrm{CH}}_3{\mathrm{COO}}^{-}$ions to form feebly ionised ${\mathrm{CH}}_3\mathrm{COOH}$ whose ionisation is further suppressed due to common ion effect. Thus, there will be a very slight effect in the overall ${\mathrm{H}}^{+}$ion concentration or $\mathrm{pH}$ value.

When a drop of $\mathrm{NaOH}$ is added, it will react with free acid to form undissociated water molecules.

$${\mathrm{CH}}_3\mathrm{COOH}+{\mathrm{OH}}^{-}\rightleftharpoons {\mathrm{CH}}_3{\mathrm{COO}}^{-}+{\mathrm{H}}_2\mathrm{O}$$

Thus, ${\mathrm{OH}}^{-}$ions furnished by a base are removed and $\mathrm{pH}$ of the solution is practically unaltered.

pH of a Buffer mixture solution (Henderson equation)

Consider a buffer mixture say an acidic buffer e.g. HA + NaA

$$\begin{array}{rl}& \mathrm{HA}\rightleftharpoons {\mathrm{H}}^{+}+{\mathrm{A}}^{-}\\ & \mathrm{NaA}\rightleftharpoons {\mathrm{Na}}^{+}+{\mathrm{A}}^{-}\end{array}$$

Applying law of equilibrium to dissociation of $\mathrm{HA}$.

$$\begin{array}{rl}& {\mathrm{K}}_{\mathrm{a}}=\frac{\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{A}}^{-}\right]}{[\mathrm{HA}]}\text{ or }\left[{\mathrm{H}}^{+}\right]=\frac{{\mathrm{K}}_{\mathrm{a}}[\mathrm{HA}]}{\left[{\mathrm{A}}^{-}\right]}\\ & \log \left[{\mathrm{H}}^{+}\right]=\log {\mathrm{K}}_{\mathrm{a}}+\log \frac{[\mathrm{HA}]}{\left[{\mathrm{A}}^{-}\right]}\end{array}$$

$$\begin{array}{rl}& -\log \left[{\mathrm{H}}^{+}\right]=-\log {\mathrm{K}}_{\mathrm{a}}+\log \frac{\left[{\mathrm{A}}^{-}\right]}{[\mathrm{HA}]}\\ & \mathrm{pH}=-{\mathrm{pK}}_{\mathrm{a}}+\log \frac{\left[{\mathrm{A}}^{-}\right]}{[\mathrm{HA}]}\\ & \mathrm{pH}={\mathrm{pK}}_{\mathrm{a}}+\log \frac{[\mathrm{Salt}]}{[\text{ Acid }]}\end{array}$$

Where, $\left[{\mathrm{A}}^{-}\right]=[$Salt $]$or [conjugate base of $\mathrm{HA}]=$ Initial concentration of the salt which is $100$ ionised. All the $\left[{\mathrm{A}}^{-}\right]$come from salt since dissociation of $\mathrm{HA}$ in presence of $\mathrm{NaA}$ is appreciably suppressed.

$[\mathrm{HA}]=[$ Acid $]=$ Intial concentration of acid since it is almost unionised in presence of $\mathrm{NaA}$.

(ii) Basic buffer

A weak base with its conjugate acid :

${\mathrm{NH}}_4\mathrm{OH}+{\mathrm{NH}}_4\mathrm{Cl}$; ( ${\mathrm{NH}}_4\mathrm{OH}$ is weak base and ${\mathrm{NH}}_4{}^{+}$is its conjugate acid).

Glycine + Glycine hydrochloride .

Blood buffer contain ${\mathrm{HCO}}_3^{-}+{\mathrm{H}}_2{\mathrm{CO}}_3$ solution to control the $\mathrm{pH}$ of blood to 7.4.

Explanation of Buffer Action

Basic buffer : Consider the case of the solution containing ${\mathrm{NH}}_4\mathrm{OH}$ and its salt ${\mathrm{NH}}_4\mathrm{Cl}$. The solution will have ${\mathrm{NH}}_4\mathrm{OH}$ molecule, ${\mathrm{NH}}_4^{+}$ions, ${\mathrm{Cl}}^{-}$ions, ${\mathrm{OH}}^{-}$ions and ${\mathrm{H}}^{+}$ions.

$$\begin{array}{rl}& {\mathrm{NH}}_4\mathrm{OH}\rightleftharpoons {\mathrm{NH}}_4^{+}+{\mathrm{OH}}^{-}(\text{Feebly ionised })\\ & {\mathrm{NH}}_4\mathrm{Cl}\rightleftharpoons {\mathrm{NH}}_4^{+}+{\mathrm{Cl}}^{-}(\text{Completely ionised })\end{array}$$

When a drop of $\mathrm{NaOH}$ is added, the added ${\mathrm{OH}}^{-}$ions combine with ${\mathrm{NH}}_4^{+}$ions to form feebly ionised ${\mathrm{NH}}_4\mathrm{OH}$ whose ionisation is further suppressed due to common ion effect. Thus, $\mathrm{pH}$ is not disturbed considerably.

${\mathrm{NH}}_4^{+}+{\mathrm{OH}}^{-}\iff {\mathrm{NH}}_4\mathrm{OH}$

(From strong base)

When a drop of $\mathrm{HCl}$ is added, the added ${\mathrm{H}}^{+}$ions combine with ${\mathrm{NH}}_4\mathrm{OH}$ to form undissociated water molecules:

$$\begin{array}{c}{\mathrm{NH}}_4\mathrm{OH}+\underset{\text{ (from strong acid)}}{{\mathrm{H}}^{+}}\rightleftharpoons {\mathrm{NH}}_4^{+}+{\mathrm{H}}_2\mathrm{O}\\ \end{array}$$

Thus, pH of the buffer is practically unaffected.

pH of a Buffer-Mixture solution (Henderson Equation)

It consists of a mixture of weak base and its salt (strong electrolyte). The ionisation of weak base $\mathrm{BOH}$ can be shown by the equation.

$$\mathrm{BOH}\rightleftharpoons {\mathrm{B}}^{+}+{\mathrm{OH}}^{-}$$

Applying law of equilibrium to dissociation of $\mathrm{BOH}$.

$$\begin{array}{rl}& {\mathrm{K}}_b=\frac{\left[{\mathrm{B}}^{+}\right]\left[{\mathrm{OH}}^{-}\right]}{[\mathrm{BOH}]}\text{ or }\left[{\mathrm{OH}}^{-}\right]=\frac{{\mathrm{K}}_b[\mathrm{BOH}]}{\left[{\mathrm{B}}^{+}\right]}\\ & \log \left[{\mathrm{OH}}^{-}\right]=\log {\mathrm{K}}_{\mathrm{b}}+\log \frac{[\mathrm{BOH}]}{\left[{\mathrm{B}}^{+}\right]}\\ & -\log \left[{\mathrm{OH}}^{-}\right]=-\log {\mathrm{K}}_{\mathrm{b}}+\log \frac{\left[{\mathrm{B}}^{+}\right]}{[\mathrm{BOH}]}\\ & \mathrm{pOH}=(+{\mathrm{pK}}_b)+\log \frac{\left[{\mathrm{B}}^{+}\right]}{[\mathrm{BOH}]}\\ & \mathrm{pOH}={\mathrm{pK}}_{\mathrm{b}}+\log \frac{[\text{ Salt }]}{[\text{ Base }]}\\ & \Rightarrow \mathrm{pH}=14-{\mathrm{pK}}_{\mathrm{b}}-\log \frac{[\text{ Salt }]}{[\text{ Base }]}\end{array}$$

Where, $\left[{\mathrm{B}}^{+}\right]=[$Salt] or [conjugate acid of $\mathrm{BOH}]=$ Initial concentration of the salt which is $100$ ionised. All the $\left[B^{†}\right]$ come from salt.

$[\mathrm{BOH}]=[$ Base $]=$ Intial concentration of base.

Utility of Buffer solutions in analytical chemistry

Buffers are used:

(i) To determine the $\mathrm{pH}$ with the help of indicators.

(ii) For the removal of phosphate ion in the qualitative inorganic analysis after second group using ${\mathrm{CH}}_3\mathrm{COOH}+{\mathrm{CH}}_3\mathrm{COONa}$ buffer.

(iii) For the precipitation of lead chromate quantitatively in gravimetric analysis, the buffer, ${\mathrm{CH}}_3\mathrm{COOH}+{\mathrm{CH}}_3\mathrm{COONa}$ is used.

(iv) For precipitation of hydroxides of third group of qualitative analysis, a buffer, ${\mathrm{NH}}_4\mathrm{Cl}+$ ${\mathrm{NH}}_4\mathrm{OH}$, is used.

(v) A buffer solution of ${\mathrm{NH}}_4\mathrm{Cl},{\mathrm{NH}}_4\mathrm{OH}$ and ${\left({\mathrm{NH}}_4\right)}_2{\mathrm{CO}}_3$ is used for precipitation of carbonates of fifth group in qualitative inorganic analysis.

Buffers are used in industrial processes such as manufacture of paper, dyes, inks. paints, drugs, etc. Buffers are also employed in agriculture, dairy products and preservation of various types of foods and fruits.

Buffer capacity and Condition for maximum buffer capacity

Buffer capacity

The property of a buffer solution to resist alteration in its $\mathrm{pH}$ value is known as buffer capacity. Buffer capacity is defined quantitatively as the number of moles of strong acid or base added in one litre of solution to change the $\mathrm{pH}$ by unity, i.e.,

Buffer capacity $(\varnothing )=\frac{\text{ Number of moles of acid or base added to }1\text{ litre }}{\text{ Change in }\mathrm{pH}}$

Thus greater the buffer capacity, the greater is the capacity of the buffer to resist change in $\mathrm{pH}$ value. Buffer capacity is greatest when the concentration of salt and weak acid/base are equal, or when $\mathrm{pH}=$ ${\mathrm{pK}}_{\mathrm{a}}$ or $\mathrm{pOH}={\mathrm{pK}}_b$.

Question . 7 How many grams of sodium acetate are required to prepare buffer solution of $\mathrm{pH}=4$ using $1\mathrm{L}$ of $\mathrm{N}/10$ acetic acid. How will the $\mathrm{pH}$ be affected when $1.5\mathrm{L}{\mathrm{H}}_2\mathrm{O}$ is added to this buffer solution (Given $K_a=2.0\times {10}^{-5}$ ).

Show Answer

Answer . A mixture of acetic acid and sodium acetate is an acidic buffer

Using Henderson equation

$$\begin{array}{rl}& \mathrm{pH}={\mathrm{pK}}_{\mathrm{a}}+\log \frac{[\text{ salt }]}{[\text{ acid }]}\\ & =-\log {\mathrm{K}}_{\mathrm{a}}+\log \frac{[\text{ salt }]}{[\text{ acid }]}\\ & \log [\text{ salt }]=\mathrm{pH}+\log {\mathrm{K}}_{\mathrm{a}}+\log [\text{ acid }]\\ & =4+\log (2.0\times {10}^{-5})+\log (0.1)\\ & =4-5+0.3010-1\\ & =-2+0.3010\end{array}$$ $[\text{ Salt }]=2\times {10}^{-2}\mathrm{M}$

$=0.02$

It is difficult to take anti log of negative number, rather than above equation we may use the same relation in the form.

$$\left[{\mathrm{H}}^{+}\right]={\mathrm{K}}_{\mathrm{a}}\frac{\text{ [acid }]}{[\text{ salt }]}$$

or $[$ salt $]=K_a\frac{[\text{ acid }]}{\left[{\mathrm{H}}^{+}\right]}=\frac{2\times {10}^{-5}\times 0.1}{{10}^{-4}}$

$=0.02$ moles of ${\mathrm{CH}}_3\mathrm{COONa}$ per litre

mass of salt $=0.02\times 82=1.64\mathrm{g}$

The addition of water ( $1.5\mathrm{L}$ ) decreases the concentration of both acid and salt, the ratio ${\log }_{10}[$ salt] / [acid] remains constant, Hence, the $\mathrm{pH}$ is unaltered.

Question . 8 $0.2\mathrm{M}$ each of $\mathrm{HCl}$ and ${\mathrm{CH}}_3\mathrm{COOH}$ are mixed in equal volumes. $20\mathrm{mL}$ of this solution is titrated against $0.1\mathrm{M}\mathrm{NaOH}$. What is the change in $\mathrm{pH}$ when $\mathrm{HCl}$ is almost completely neutralised. (given ${\mathrm{K}}_{\mathrm{a}}\left({\mathrm{CH}}_3\mathrm{COOH}\right)=2.0\times {10}^{-5})$.

Show Answer

Answer . Since the two solution are mixed in equal volumes therefore, the concentration of $\mathrm{HCl}$ and ${\mathrm{CH}}_3\mathrm{COOH}$ in the resulting solution is $0.1\mathrm{M}$ each.

The presence of strong acid in a mixture suppresses the ionization of weak acid therefore, before the start of the titration, $\mathrm{pH}$ of the solution depends only on the ${\mathrm{H}}^{+}$ions furnished by $\mathrm{HCl}$.

$$\therefore pH=1$$

After neutralization of ${\mathrm{H}}^{+}$ions furnished by $\mathrm{HCl}$ with $\mathrm{NaOH}$, volume of the solution doubles.

$\therefore$ Concentration of acetic acid is calculated as

$$\begin{array}{rl}& \underset{\text{ (before neutralization) }}{{\mathrm{M}}_1{\mathrm{V}}_1}=\begin{array}{c}{\mathrm{M}}_2{\mathrm{V}}_2\\ \text{ (after neutralization) }\end{array}\\ & {\mathrm{M}}_2=\frac{0.1\times 20}{40}=0.05\mathrm{M}\end{array}$$

For a weak acid

$$\begin{array}{rl}& \left[{\mathrm{H}}^{+}\right]=\sqrt{{\mathrm{K}}_{\mathrm{a}}\mathrm{C}}\\ & =\sqrt{2\times {10}^{-5}\times 0.05}\\ & ={10}^{-3}\\ & \mathrm{pH}=3\end{array}$$

Change in $\mathrm{pH}=3-1=2$

The $\mathrm{pH}$ of the solution changes by 2 units.

PRACTICE QUESTIONS

1. One litre of a buffer solution containing $0.01\mathrm{M}{\mathrm{NH}}_4\mathrm{Cl}$ and $0.1\mathrm{M}{\mathrm{NH}}_4\mathrm{OH}$ having ${\mathrm{pK}}_b$ of 5 has $\mathrm{pH}$ of

(a) 9

(b) 10

(c) 4

(d) 6

Show Answer

Answer: (b)

2. The approximate $\mathrm{pH}$ of a solution formed by mixing equal volumes of solutions of $0.1\mathrm{M}$ sodium propanoate and $0.1\mathrm{M}$ propanoic acid (the dissociation constant of propanoic acid is $1.3\times {10}^{-5}$ mol ${\mathrm{dm}}^{-3}$ ) will be

(a) $1.52$

(b) $3.62$

(c) $4.89$

(d) $5.52$

Show Answer

Answer: (c)

3. A certain buffer solution contains equal concentration of ${\mathrm{X}}^{-}$and $\mathrm{HX}$. The ${\mathrm{K}}_{\mathrm{a}}$ for $\mathrm{HX}$ is ${10}^{-8}$. The $\mathrm{pH}$ of the buffer is

(a) 3

(b) 8

(c) 11

(d) 14

Show Answer

Answer: (b)

4. The ${\mathrm{pK}}_{\mathrm{a}}$ of $\mathrm{HCN}$ is 9.30 . The $\mathrm{pH}$ of a solution prepared by mixing 2.5 moles of $\mathrm{KCN}$ and 2.5 moles of $\mathrm{HCN}$ in water and making up the total volume of $500\mathrm{mL}$ is

(a) $9.30$

(b) $7.30$

(c) $10.30$

(d) $8.30$

Show Answer

Answer: (a)

5. A certain buffer solution contains equal concentrations of ${\mathrm{X}}^{-}$and $\mathrm{HX}$. ${\mathrm{K}}_{\mathrm{b}}$ for ${\mathrm{X}}^{-}$is ${10}^{-10}$. The $\mathrm{pH}$ of the buffer solution is

(a) 4

(b) 10

(c) 7

(d) 14

Show Answer

Answer: (a)

6. In a mixture of a weak acid and its salt, the ratio of the concentration of acid to salt is increased tenfold. The pH of the solution

(a) decreases by one

(b) decreases by one tenth

(c) increases by one

(d) increases ten-fold

Show Answer

Answer: (a)

7. How much sodium acetate should be added to $0.1\mathrm{M}$ solution of ${\mathrm{CH}}_3\mathrm{COOH}$ to give a solution of pH5.5 $({\mathrm{pK}}_{\mathrm{a}}$ of ${\mathrm{CH}}_3\mathrm{COOH}=4.5)$

(a)$0.1\mathrm{M}$

(b) $0.2\mathrm{M}$

(c) $1.0\mathrm{M}$

(d) $10.0\mathrm{M}$

Show Answer

Answer: (c)

8. For preparing a buffer solution of $\mathrm{pH}=6$ by mixing sodium acetate and acetic acid, the concentration of salt and acid should be $(K_a={10}^{-5})$

(a) $1:10$

(b) $10:1$

(c) $100:1$

(d) $1:100$

Show Answer

Answer: (b)

9. A buffer solution is prepared by mixing $10\mathrm{mL}$ of $1.0\mathrm{M}$ acetic and $20\mathrm{mL}$ of $0.5\mathrm{M}$ sodium acetate and then diluted to $100\mathrm{ml}$ with distilled water. If the ${\mathrm{pK}}_{\mathrm{a}}$ of ${\mathrm{CH}}_3\mathrm{COOH}$ is 4.76 , what is the $\mathrm{pH}$ of the buffor solution prepared?

(a) $5.21$

(b) $4.76$

(c) $4.34$

(d) $5.21$

Show Answer

Answer: (b)

10. What is $\left[{\mathrm{H}}^{+}\right]$of a solution that is $0.1\mathrm{M}\mathrm{HCN}$ and $0.2\mathrm{M}\mathrm{NaCN}$ ? $({\mathrm{K}}_{\mathrm{a}}$ for $\mathrm{HCN}=6.2\times {10}^{-10}$ )

(a) $3.1\times {10}^{10}$

(b) $6.2\times {10}^5$

(c) $6.2\times {10}^{-10}$

(d) $3.1\times {10}^{-10}$

Show Answer

Answer: (d)

11. The $\mathrm{pH}$ of a buffer containing equal molar concentrations of a weak base and its chloride ( ${\mathrm{K}}_{\mathrm{b}}$ for weak base $=2\times {10}^{-5},\log 2=0.3$ ) is

(a) $5$

(b) $9$

(c) $4.7$

(d) $9.3$

Show Answer

Answer: (d)

12. Solution of $0.1{\mathrm{NNH}}_4\mathrm{OH}$ and $0.1{\mathrm{NNH}}_4\mathrm{Cl}$ has $\mathrm{pH}$ 9.25. Then ${\mathrm{pK}}_6$ of ${\mathrm{NH}}_4\mathrm{OH}$ is

(a) $9.25$

(b) $4.75$

(c) $3.75$

(d) $8.25$

Show Answer

Answer: (b)

13. The most important buffer in the blood consists of:

(a) ${\mathrm{HCl}}^{-}$and ${\mathrm{Cl}}^{-}$

(b) ${\mathrm{H}}_2{\mathrm{CO}}_3$ and ${\mathrm{HCO}}_3^{-}$

(c) ${\mathrm{H}}_2{\mathrm{CO}}_3$ and ${\mathrm{Cl}}^{-}$

(d) $\mathrm{HCl}$ and ${\mathrm{HCO}}_3^{-}$

Show Answer

Answer: (b)

14. The pH of blood is maintained by the balance between ${\mathrm{H}}_2{\mathrm{CO}}_3$ and ${\mathrm{NaHCO}}_3$. If the amount of ${\mathrm{CO}}_2$ in the blood is increased, how will it effect the pH of blood

(a) $\mathrm{pH}$ will increase

(b) $\mathrm{pH}$ will decrease

(c) $\mathrm{pH}$ will be 7

(d) $\mathrm{pH}$ will remain same

Show Answer

Answer: (b)

SOLUBILITY PRODUCT

Solution which remains in equilibrium with undissolved solute (salt) is said to be saturated. At saturation stage, the quantity of the salt dissolved is always constant, for the given amount of a particular solvent at a definite temperature. This is referred to as the solubility of the given salt at the given temperature.

In a saturated solution of a salt the following equilibrium exists :

$$\mathrm{AB}(\mathrm{s})\rightleftharpoons {\mathrm{A}}^{+}+{\mathrm{B}}^{-}$$

Applying the law of equilibrium to the ionic equilibrium,

$$\frac{\left[A^{+}\right]\left[B^{-}\right]}{[AB]}=K$$

Since, the concentration of the solid salt is constant at a particular temperature, i.e., $[AB]=$ constant.

Hence, $\left[{\mathrm{A}}^{+}\right]\left[{\mathrm{B}}^{-}\right]={\mathrm{K}}_{\mathrm{sp}}$ (constant)

${\mathrm{K}}_{\mathrm{sp}}$ is termed as the solubility product, It is defined as the product of the concentration of ions in a saturated solution of an electrolyte at a given temperature.

Relationship between Solubility and Solubility Product

The equilibrium for a saturated solution of any sparingly soluble salt may be expressed as :

$A_x{B}_y(s)\rightleftharpoons x{A}^{y+}+y{B}^{x-}$

Thus, solubility product, ${\mathrm{K}}_{\mathrm{sp}}={\left[{\mathrm{A}}^{\mathrm{y}+}\right]}^{\mathrm{x}}{\left[{\mathrm{B}}^{\mathrm{x}}\right]}^{\mathrm{y}}$

Let ’ $s$ ’ mol per litre be the solubility of the salt; then

$\begin{array}{rl}& {\mathrm{A}}_{\mathrm{x}}{\mathrm{B}}_{\mathrm{y}}(\mathrm{s})\rightleftharpoons \mathrm{x}{\mathrm{A}}^{\mathrm{y}+}+\mathrm{y}{\mathrm{B}}^{\mathrm{x}}\\ & \text{ xs qquad ys }\end{array}$

So, ${\mathrm{K}}_{\mathrm{sp}}=[\mathrm{xs}{]}^{\mathrm{x}}[\mathrm{ys}{]}^{\mathrm{y}}$

$=x^x\cdot y^y(s{)}^{x+y}$

(i) 1:1 (AB) type salts:

Examples: $\mathrm{AgCl},\mathrm{Agl},{\mathrm{BaSO}}_4,{\mathrm{PbSO}}_4$, etc.

Binary electrolyte : $\mathrm{AB}(\mathrm{s})\rightleftharpoons {\mathrm{A}}^{+}+{\mathrm{B}}^{-}$

$\mathrm{S}\mathrm{S}$

Let solubility of $AB$ be ’ $s$ ’ $\mathrm{mol}{\mathrm{L}}^{-1}$.

So, $K_{sp}=\left[A^{+}\right]\left[B^{-}\right]=sxS=s^2$

or $\mathrm{S}=\sqrt{{\mathrm{K}}_{\mathrm{sp}}}$

(ii) $1:2\left({\mathrm{AB}}_2\right)$ or $2:1\left({\mathrm{A}}_2\mathrm{B}\right)$ type salts:

Examples: ${\mathrm{Ag}}_2{\mathrm{CO}}_3,{\mathrm{Ag}}_2{\mathrm{CrO}}_4,{\mathrm{PbCl}}_2,{\mathrm{CaF}}_2$, etc.

Ternary electrolyte: ${\mathrm{AB}}_2(\mathrm{s})\rightleftharpoons {\mathrm{A}}^{2+}+2{\mathrm{B}}^{-}$

$S2s$

Let solubility of $A{B}_2$ be ’ $s$ ’ $\mathrm{mol}{\mathrm{L}}^{-1}$

So, $K_{sp}=\left[A^{2+}\right]{\left[B^{-}\right]}^2=s\times (2s{)}^2=4s^3$

or $\mathrm{S}=3\sqrt{{\mathrm{K}}_{\mathrm{sp}}/4}$

${\mathrm{A}}_2\mathrm{B}(\mathrm{s})\rightleftharpoons 2{\mathrm{A}}^{+}+{\mathrm{B}}^{2-}$

$2\mathrm{s}s$

Let ’ $s$ ’ be the solubility of $A_{2}B$.

${\mathrm{K}}_{\mathrm{sp}}={\left[{\mathrm{A}}^{+}\right]}^2\left[{\mathrm{B}}^{2-}\right]$

$=(2\mathrm{s}{)}^2(\mathrm{s})=4{\mathrm{s}}^3$

or $\mathrm{S}=\sqrt[3]{{\mathrm{K}}_{\mathrm{sp}}/4}$

(iii) 1:3 (AB) type salts:

Examples: ${\mathrm{All}}_3,\mathrm{Fe}(\mathrm{OH}{)}_3,\mathrm{Cr}(\mathrm{OH}{)}_3,\mathrm{Al}(\mathrm{OH}{)}_3$, etc.

Quaternary electrolyte: ${\mathrm{AB}}_3(\mathrm{s})\rightleftharpoons {\mathrm{A}}^{3+}+3{\mathrm{B}}^{-}$

$s3\mathrm{s}$

Let ’ $s$ ’ mol litre ${}^{-1}$ be the solubility of $A{b}_3$.

$$K_{sp}=\left[A^{3+}\right]{\left[B^{-}\right]}^3=s\times (3s{)}^3=27s^4\text{ or }s=\sqrt[4]{K_{sp}/27}$$

The presence of a common ion affects the solubility of a salt. Let $AB$ be a sparingly soluble salt in solution and $A^{\prime }B$ be added to it. Let $s$ and $s^{\prime }$ be the solubilities of the salt $AB$ before and after addition of the electrolyte $A^{\prime }B$. Let $c$ be the concentration of $A^{\prime }B$.

Before addition of $A^{\prime }B,K_{sp}=s^2$ …..(i)

After addition of $A^{\prime }B$, the concentration of $A^{+}$and $B^{-}$ions becomes’ and $(s^{\prime }+c)$, respectively.

So, $K_{sp}=s^{\prime }(s^{\prime }+c)$…..(ii)

Equating Eqns. (i) and (ii)

$\begin{array}{rl}& {\mathrm{s}}^2={\mathrm{s}}^{\prime }({\mathrm{s}}^{\prime }+\mathrm{c})\\ \therefore & {\mathrm{s}}^{\prime }<\mathrm{s}\end{array}$

Thus, the solubility of the salt decreases due to common ion effect

Important Cases of Calculating Solubility of a Salt

(i) Solubility of a salt of strong acid and strong base $(\mathrm{AgCl})$ in pure water

(a) in the absence of common ion

$\mathrm{AgCl}(\mathrm{s})\rightleftharpoons {\mathrm{Ag}}^{+}(\mathrm{aq})+{\mathrm{Cl}}^{-}(\mathrm{aq})$

${\mathrm{K}}_{\mathrm{sp}}=\mathrm{s}$. $\mathrm{S}$ or $\mathrm{S}=\sqrt{{\mathrm{K}}_{\mathrm{sp}}}$

(b) In the presence of common ion say $\left[{\mathrm{Ag}}^{+}\right]=$’ $\mathrm{a}$ ’ moles $/\mathrm{L}$

${\mathrm{K}}_{\mathrm{sp}}=({\mathrm{s}}^{\prime }+\mathrm{a})\left({\mathrm{s}}^{\prime }\right)$

$s^{\prime }$ will be less than $s$.

(ii) Solubility of a salt of weak acid and strong base $\left({\mathrm{CH}}_3\mathrm{COOAg}\right)$.

(a) In pure water

${\mathrm{CH}}_3\mathrm{COOAg}\rightleftharpoons {\mathrm{CH}}_3{\mathrm{COO}}^{-}(\mathrm{aq})+{\mathrm{Ag}}^{+}(\mathrm{aq})$

since it is a salt of weak acid and strong base, it will undergo anionic hydrolysis

${\mathrm{CH}}_3\mathrm{COOAg}(\mathrm{s})\rightleftharpoons {\mathrm{CH}}_3{\mathrm{COO}}^{-}(\mathrm{aq})+{\mathrm{Ag}}^{+}(\mathrm{aq})$

${\mathrm{CH}}_3{\mathrm{COO}}^{-}(\mathrm{aq})+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{CH}}_3\mathrm{COOH}+{\mathrm{OH}}^{-}(\mathrm{aq})$

Since the concentration of ${\mathrm{CH}}_3{\mathrm{COO}}^{-}$ion decreases due to hydrolysis, the solubility equilibrium would shift in the forward direction and the solubility of the salt ${\mathrm{CH}}_3\mathrm{COOAg}$ would increase.

(b) In the presence of an acid

The following equilibrium is also quickly established

${\mathrm{CH}}_3{\mathrm{COO}}^{-}(\mathrm{aq})+{\mathrm{H}}^{+}(\mathrm{aq})\rightleftharpoons {\mathrm{CH}}_3\mathrm{COOH}(\mathrm{aq})+{\mathrm{H}}_2\mathrm{O}(\mathrm{aq})$

Since ${\mathrm{CH}}_3{\mathrm{COO}}^{-}$ions combine with ${\mathrm{H}}^{+}$ions of the acid, its concentration decreases. According to the Le Chatelier’s principle, the solubility equilibrium of ${\mathrm{CH}}_3\mathrm{COOAg}$ would shift in the forward direction there by increasing its solubility.

(c) in the presence of basic buffer

Here, hydrolysis of ${\mathrm{CH}}_3{\mathrm{COO}}^{-}$is in the presence of basic medium is suppressed

Thus, solubility of such salts is maximum in acidic solution, then in pure water and then in basic solution.

(iii) Solubility of a salt of strong acid and weak base $({\mathrm{C}}_6{\mathrm{H}}_5{\mathrm{NH}}_3{}^{+}\mathrm{C}-{}^{-})$

Such salts have maximum solubility in a basic solution then in pure water and then in an acidic solution.

(iv) Solubility of a salt of weak acid and weak base $\left({\mathrm{CH}}_3{\mathrm{COONH}}_4\right)$

in pure water

${\mathrm{CH}}_3{\mathrm{COONH}}_4(\mathrm{s})\rightleftharpoons {\mathrm{CH}}_3{\mathrm{COO}}^{-}(\mathrm{aq})+{\mathrm{NH}}_4^{+}(\mathrm{aq})$

on hydrolysis

${\mathrm{NH}}_4^{+}(\mathrm{aq})+{\mathrm{CH}}_3{\mathrm{COO}}^{-}(\mathrm{aq})+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{NH}}_3\mathrm{OH}(\mathrm{aq})+{\mathrm{CH}}_3\mathrm{COOH}$

Solubility of such salts would increase in presence of both, an acid or a base.

Criteria of precipitation of an electrolyte

A very useful conclusion is derived from the solubility product concept. No precipitation of the electrolyte occurs if the ionic product $\left(K_{\mathrm{ip}}\right)$ refers to $Q_{sp}$ (reaction quotient) of a sparingly soluble salt at any specified concentration at a given temperature is less than the solubility product, i.e., the solution has not reached the saturation stage.

Case I: When ${\mathrm{K}}_{\mathrm{ip}}<{\mathrm{K}}_{\mathrm{sp}}$, then solution is unsaturated in which more solute can be dissolved.

Case II: When ${\mathrm{K}}_{\mathrm{ip}}={\mathrm{K}}_{\mathrm{sp}}$, then solution is saturated in which no more solute can be dissolved.

Case III: When ${\mathrm{K}}_{\mathrm{ip}}>{\mathrm{K}}_{\mathrm{sp}}$, then solution is super-saturated and precipitation takes place.

When the ionic product exceeds the solubility product, the equilibrium shifts towards left hand side resulting in precipitation of the salt.

Thus, for the precipitation of an electrolyte, it is necessary that the ionic product must exceed its solubility product. For example, if equal volumes of $0.02\mathrm{M}{\mathrm{AgNO}}_3$ solution and $0.02\mathrm{M}{\mathrm{K}}_2{\mathrm{CrO}}_4$ solution are mixed, the precipitation of ${\mathrm{Ag}}_2{\mathrm{CrO}}_4$ occurs as the ionic product exceeds the solubility product of ${\mathrm{Ag}}_2{\mathrm{CrO}}_4$ which is $2\times {10}^{-12}$

In the resulting solution,

$\left[{\mathrm{Ag}}^{+}\right]=\frac{0.02}{2}=0.01=1\times {10}^{-2}\mathrm{M}$

and $\left[{\mathrm{CrO}}_4{}^{2-}\right]=\frac{0.02}{2}=0.01=1\times {10}^{-2}\mathrm{M}$

lonic product of ${\mathrm{Ag}}_2{\mathrm{CrO}}_4={\left[{\mathrm{Ag}}^{+}\right]}^2\left[{\mathrm{CrO}}_4{}_4^{2-}\right]$

$$\begin{array}{rl}& ={(1\times {10}_{-2})}^2(1\times {10}^{-2})\\ & =1\times {10}^{-6}\end{array}$$

$1\times {10}^{-6}$ is higher than $2\times {10}^{-12}$ and thus precipitation of ${\mathrm{Ag}}_2{\mathrm{CrO}}_4$ occurs.

Applications of solubility product

(i) Salting out of soap:

Soap is a sodium salt of higher fatty acids. From the solution, soap is precipitated by the addition of concentrated solution of sodium chloride. Soap and sodium chloride are present in the form of ions.

$$\begin{array}{rl}& {\mathrm{C}}_n{\mathrm{H}}_{2n+1}\mathrm{COONa}\rightleftharpoons {\mathrm{C}}_n{\mathrm{H}}_{2n+1}{\mathrm{COO}}^{-}+{\mathrm{Na}}^{+}\\ & \text{Soap }\\ & \mathrm{NaCl}\rightleftharpoons {\mathrm{Na}}^{+}+{\mathrm{Cl}}^{-}\end{array}$$

Thus, the concentration of ${\mathrm{Na}}^{+}$ions increases considerably on addition of $\mathrm{NaCl}$ solution. Hence, the ionic product $\left[{\mathrm{C}}_n{\mathrm{H}}_{2n+1}{\mathrm{COO}}^{-}\right]\left[{\mathrm{Na}}^{+}\right]$exceeds the solubility product of soap and therefore, soap precipitates out from the solution.

(ii) Precipitation of the sulphides of group II and IV:

Hydrogen sulphide is a weak electrolyte and is used for the precipitation of various sulphides of group II and IV in qualitative analysis.

Passing ${\mathrm{H}}_2\mathrm{S}(\mathrm{g})$ in an aqueous solution:

${\mathrm{H}}_2\mathrm{S}$ is a dibasic acid. We have to visualize two stage ionisation for it as follows:

$$\begin{array}{ll}{\mathrm{H}}_2\mathrm{S}(\mathrm{aq})\rightleftharpoons {\mathrm{H}}^{+}(\mathrm{aq})+{\mathrm{HS}}^{-}(\mathrm{aq});& {\mathrm{K}}_1\dots \dots ..(i)\\ {\mathrm{HS}}^{-}(\mathrm{aq})\rightleftharpoons {\mathrm{H}}^{+}(\mathrm{aq})+{\mathrm{S}}^{2-}(\mathrm{aq});& {\mathrm{K}}_2\dots \dots ..(ii)\end{array}$$

${\mathrm{K}}_1$ and ${\mathrm{K}}_2$ are two ionisation constants respectively for ${\mathrm{H}}_2\mathrm{S}(\mathrm{aq}$ ). Since ${\mathrm{K}}_2«{\mathrm{K}}_1$ (due to common ion effect), we usually neglect the concentration of ${\mathrm{H}}^{+}$ions from second equilibrium.

${\left[{\mathrm{H}}^{+}\right]}_{\mathrm{in}\mathrm{Solution}}={\left[{\mathrm{H}}^{+}\right]}_{\mathrm{from}\mathrm{H}{\mathrm{H}}_2\mathrm{S}}+{\left[{\mathrm{H}}^{+}\right]}_{\text{from Hs }}={\left[{\mathrm{H}}^{+}\right]}_{\text{from }{\mathrm{H}}_2\mathrm{S}}$

Now $K_1=\frac{\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{HS}}^{-}\right]}{\left[{\mathrm{H}}_2\mathrm{S}\right]}$ and ${\mathrm{K}}_2=\frac{\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{S}}^{2-}\right]}{\left[{\mathrm{HS}}^{-}\right]}$

From (i), $\left[{\mathrm{H}}^{+}\right]=\left[{\mathrm{HS}}^{-}\right]$and neglecting $\left[{\mathrm{H}}^{+}\right]$from (ii) we have from second ionisation constant:

${\mathrm{K}}_2=\frac{\left[{\mathrm{H}}^{-}\right]\left[{\mathrm{HS}}^{2-}\right]}{\left[{\mathrm{HS}}^{-}\right]}=\left[{\mathrm{S}}^{2-}\right]\text{ or }\left[{\mathrm{S}}^{2-}\right]={\mathrm{K}}_2$

So if we pass ${\mathrm{H}}_2\mathrm{S}$ in an aqueous solution, sulphide ion concentration is simply equal to the value of second ionisation constant. We can determine whether precipitation of metal sulphide will occur or not by comparing ionic product (I.P.) with solubility constant $\left({\mathrm{K}}_{\mathrm{sp}}\right)$.

Passing ${\mathrm{H}}_2\mathrm{O}(\mathrm{g})$ in an acidic or a basic solution :

Now if we pass ${\mathrm{H}}_2\mathrm{S}$ in an acidic solution of a metal ion till saturation, we simply neglect the concentration of ${\mathrm{H}}^{+}$ion from ${\mathrm{H}}_2\mathrm{S}$ (both from first and second ionisations) totally as the concentration of ${\mathrm{H}}^{+}$from acid (Strong acid added externally) is very high. In that case we can simply add two equilibriums (i) and (ii) to get :

$$\begin{array}{rl}& {\mathrm{H}}_2\mathrm{S}(\mathrm{aq})\rightleftharpoons 2{\mathrm{H}}^{+}(\mathrm{aq})+{\mathrm{S}}_2^{-}(\mathrm{aq});{\mathrm{K}}_{\mathrm{a}\left({\mathrm{H}}_2\mathrm{S}\right)}\\ & {\mathrm{K}}_{\mathrm{a}}={\mathrm{K}}_1\times {\mathrm{K}}_2=\frac{{\left[{\mathrm{H}}^{+}\right]}^2\left[{\mathrm{S}}^{2-}\right]}{\left[{\mathrm{H}}_2\mathrm{S}\right]}\end{array}$$

Note that in a saturated solution of ${\mathrm{H}}_2\mathrm{S}$ at ${25}^{\circ }\mathrm{C},\left[{\mathrm{H}}_2\mathrm{S}\right]$ is constant at $0.1\mathrm{M}$.

$$\begin{array}{rl}& {\mathrm{K}}_{\mathrm{a}}\mathrm{X}(0.1\mathrm{M})={\left[{\mathrm{H}}^{+}\right]}^2\left[{\mathrm{S}}^{2-}\right]\\ & {\left[{\mathrm{H}}^{+}\right]}^2\left[{\mathrm{S}}^{2-}\right]={\mathrm{K}}_{\mathrm{sp}}\left({\mathrm{of}}_2\mathrm{S}\right)\\ & \left[{\mathrm{S}}^{2-}\right]=\frac{{\mathrm{K}}_{\mathrm{a}}\times (0.1\mathrm{M})}{{\left[{\mathrm{H}}^{+}\right]}^2}=\frac{{\mathrm{K}}_1\times {\mathrm{K}}_2\times (0.1\mathrm{M})}{{\left[{\mathrm{H}}^{+}\right]}^2}\end{array}$$

In this way, we now know the concentration of sulphide ions in an acidic solution, so accordingly we can plan precipitation of metal ions. The important aspect of this method is that we can always increase or decrease the concentration of sulphide ion by controlling the amount of acid. In acidic medium (II group), $\left[{\mathrm{H}}^{+}\right]$is high and $\left[{\mathrm{S}}^{2-}\right]$ is low. It is enough to precipitate group II cations, where sulphides have very small solubility products. In basic medium (IV group), $\left[{\mathrm{H}}^{+}\right]$is very low and $\left[{\mathrm{S}}^{2-}\right]$ is relatively high. Now it is sufficient to precipitate the cations of group IV as sulphides which have relatively high values of solubility product.

(iii) Precipitation of hydroxides of Group III:

Ammonium hydroxide is a precipitating agent in Group III of the qualitative analysis. It is a weak electrolyte and ionises in water as

$${\mathrm{NH}}_4\mathrm{OH}\rightleftharpoons {\mathrm{NH}}_4^{+}+{\mathrm{OH}}^{-}$$

The concentration of ${\mathrm{OH}}^{-}$ions is so large that not only the hydroxides of group III $[\mathrm{Fe}(\mathrm{OH}{)}_3,\mathrm{Cr}(\mathrm{OH}{)}_3$ and $\mathrm{Al}(\mathrm{OH}{)}_3]$ but the hydroxides of higher groups also get precipitated. The solubility products of various hydroxides are given below:

$\begin{array}{ll}\mathrm{Fe}(\mathrm{OH}{)}_3& 11\times {10}^{-36}\\ \mathrm{Cr}(\mathrm{OH}{)}_3& 3\times {10}^{-29}\\ \mathrm{Al}(\mathrm{OH}{)}_3& 8.5\times {10}^{-23}\end{array}]$ Group III, low values

$\begin{array}{ll}\mathrm{Zn}(\mathrm{OH}{)}_2& 1.8\times {10}^{-17}\\ \mathrm{Mn}(\mathrm{OH}{)}_2& 4\times {10}^{-14}\\ \mathrm{Mg}(\mathrm{OH}{)}_2& 3.4\times {10}^{-11}\end{array}]$ high values

In order to precipitate only the hydroxides of group III, the ${\mathrm{OH}}^{-}$ions concentration must be lowered. This is achieved by the use of ammonium chloride before the addition of ammonium hydroxide. The increased concentration of ${\mathrm{NH}}_4{}^{+}$ions suppresses the ionisation of ${\mathrm{NH}}_4\mathrm{OH}$ due to common ion effect. Under this condition, the ionic products of hydroxides of group III alone exceed their solubility products and therefore, get precipitated.

(v) Using excess of precipitating agent in gravimetric analysis:

So as to ensure complete precipitation in gravimetric analysis, an excess of precipitating agent is always used. In gravimetric analysis, barium is precipitated as barium sulphate. No doubt, ${\mathrm{BaSO}}_4$ is a sparingly soluble substance but it possesses a measurable solubility. To decrease its solubility, the concentration of ${\mathrm{SO}}_4{}^{2-}$ ions is increased by use of little excess of ${\mathrm{H}}_2{\mathrm{SO}}_4$. The ionic product $\left[{\mathrm{Ba}}^{2+}\right]\left[{\mathrm{SO}}_4^2\right]$ exceeds the solubility product of ${\mathrm{BaSO}}_4$ and it is precipitated more completely.

Question. 9 The solubility of ${\mathrm{BaSO}}_4$ in water is $2.33\times {10}^{-4}\mathrm{g}/100\mathrm{mL}$. Calculate the percentage loss in weight when $0.3\mathrm{g}$ of ${\mathrm{BaSO}}_4$ is washed with $1.5\mathrm{L}$ of $0.01{\mathrm{NH}}_2{\mathrm{SO}}_4$. (Molar mass $\left({\mathrm{BaSO}}_4\right)=233\mathrm{g}/\mathrm{mole})$.

Show Answer

Answer . Loss in weight of ${\mathrm{BaSO}}_4=$ amount of ${\mathrm{BaSO}}_4$ soluble

$$\begin{array}{rl}& 0.01\mathrm{N}{\mathrm{NH}}_2{\mathrm{SO}}_4=0.01\mathrm{N}{\mathrm{SO}}_4^{2-}\text{ ions }\\ & =0.005\mathrm{M}{\mathrm{SO}}_4^{2-}\text{ ions }\end{array}$$

The presence of ${\mathrm{SO}}_4{}^{2-}$ ions in the solution will suppress the solubility of ${\mathrm{BaSO}}_4$ (due to common ion effect). The extent of suppression is governed by solubility product of salt.

$${\mathrm{K}}_{\mathrm{sp}}=\left[{\mathrm{Ba}}^{2+}\right]\left[{\mathrm{SO}}_4^{2-}\right]$$

Given solubility $=2.33\times {10}^{-4}\mathrm{g}/100\mathrm{mL}$

$$\begin{array}{rl}& =2.33\times {10}^{-3}\mathrm{g}/\mathrm{L}\\ & =\frac{2.33}{233}\times {10}^{-3}={10}^{-5}\mathrm{M}\\ & \therefore {\mathrm{K}}_{\mathrm{sp}}=\left[{\mathrm{Ba}}^{2+}\right]\left[{\mathrm{SO}}_4^{2-}\right]\\ & ={\left({10}^{-5}\right)}^2={10}^{-10}\end{array}$$

Let ’ $x$ ’ be the solubility in $\mathrm{mol}/{\mathrm{Lin}}^2{\mathrm{H}}_2{\mathrm{SO}}_4$

$\left[{\mathrm{Ba}}^{2+}\right]$ in solution $=\mathrm{x}$

$\left[{\mathrm{SO}}_4^{2-2}\right]$ in solution $=(x+0.005)$

lonic product $=\left[{\mathrm{Ba}}^{2+}\right]\left[{\mathrm{SO}}_4^{2-}\right]$

$=(x)(x+0.005)$

At equilibrium

$\begin{array}{rl}& \text{ lonic product }={\mathrm{K}}_{\mathrm{sp}}\\ \Rightarrow & 1.0\times {10}^{-10}=(\mathrm{x})(\mathrm{x}+0.005)\approx 0.005\mathrm{x}\\ \Rightarrow & \mathrm{x}=\frac{1.0\times {10}^{-10}}{0.005}=2\times {10}^{-8}\mathrm{M}\\ \Rightarrow & \mathrm{x}=2\times {10}^{-8}\times 233=4.66\times {10}^{-6}\mathrm{g}/\mathrm{L}\end{array}$

$$\begin{array}{rl}& 4.66\times {10}^{-6}\mathrm{g}\text{ of }{\mathrm{BaSO}}_4\text{ is washed away with }1\mathrm{L}\text{ of given solution }\\ & \Rightarrow 6.99\times {10}^{-6}\mathrm{g}{\mathrm{BaSO}}_4\text{ is washed away with }1.5\mathrm{L}\text{ of given solution }\\ & \Rightarrow \text{ percentage loss }=\frac{6.99\times {10}^{-6}\times 100}{0.3}\\ & =2.33\times {10}^{-3}\mathrm{\%}\end{array}$$

Question. 10 The solubility product ${\mathrm{K}}_{\mathrm{sp}}$ of $\mathrm{Ca}(\mathrm{OH}{)}_2$ at ${25}^{\circ }\mathrm{C}$ is $4.0\times {10}^{-6}$. A $200\mathrm{mL}$ of saturated solution of $\mathrm{Ca}(\mathrm{OH}{)}_2$ is mixed with equal volume of $0.5\mathrm{M}\mathrm{NaOH}$. How many moles of $\mathrm{Ca}(\mathrm{OH}{)}_2$ are precipitated?

Show Answer

Answer . The first step is to determine the concentration of ${\mathrm{Ca}}^{2+}$ at saturation using ${\mathrm{K}}_{\mathrm{sp}}$

$$\begin{array}{rl}& \mathrm{Ca}(\mathrm{OH}{)}_2\rightleftharpoons {\mathrm{Ca}}^{2+}+2{\mathrm{OH}}^{-}\\ & K_{sp}=(x)(2x{)}^2\\ & {\mathrm{K}}_{\mathrm{sp}}=4{\mathrm{x}}^3\\ & \Rightarrow x=\sqrt[3]{\frac{K_{sp}}{4}}=\sqrt[3]{\frac{4\times {10}^{-6}}{4}}=0.01\mathrm{M}\\ & \Rightarrow \left[{\mathrm{Ca}}^{2+}\right]=0.01\mathrm{M};\left[{\mathrm{OH}}^{-}\right]=0.02\mathrm{M}\\ & \left[{\mathrm{Ca}}^{2+}\right]=\frac{0.01}{2}=0.005\mathrm{M}\\ & \left[{\mathrm{OH}}^{-}\right]=\frac{0.02}{2}+\frac{0.5}{2}\text{ (due to common ion) }\\ & =0.26\mathrm{M}\end{array}$$

Ionic product of salt in the solution

$\begin{array}{rl}& =(0.005)(0.26{)}^2\\ & =3.38\times {10}^{-4}>{\mathrm{K}}_{\mathrm{sp}}(4.0\times {10}^{-6})\end{array}$

${\mathrm{Ca}}^{2+}$ will be precipitated till a new saturation stage is reached where

$\left[{\mathrm{OH}}^{-}\right]=0.26\mathrm{M}$ (as present in excess, its concentration remains unchanged)

At this stage

$$\begin{array}{rl}\left[{\mathrm{Ca}}^{2+}\right]& =\frac{{\mathrm{K}}_{\mathrm{sp}}}{{\left[{\mathrm{OH}}^{-}\right]}^2}=\frac{4\times {10}^{-6}}{(0.26{)}^2}\\ & =5.917\times {10}^{-5}\mathrm{M}\\ \Rightarrow \left[{\mathrm{Ca}}^{2+}\right]& \text{ precipitated }=5\times {10}^{-3}-5.917\times {10}^{-5}\\ & =4.94\times {10}^{-3}\mathrm{M}\end{array}$$

i.e. $4.94\times {10}^{-3}{\mathrm{mole}}^2$ of ${\mathrm{Ca}}^{2+}$ is precipitated.

Question. 11 What is the solubility of $\mathrm{AgCN}$ in a buffer solution of $\mathrm{pH}=2$.

Given ${\mathrm{K}}_{\mathrm{sp}}(\mathrm{AgCN})=2\times {10}^{-6};{\mathrm{K}}_{\mathrm{a}}(\mathrm{HCN})=6.0\times {10}^{-10}$

Show Answer

Answer . $\mathrm{AgCN}(\mathrm{s})\rightleftharpoons {\mathrm{Ag}}^{+}(\mathrm{aq})+{\mathrm{CN}}^{-}(\mathrm{aq})$

Let the solubility of the salt be $x\mathrm{M}$.

The ${\mathrm{CN}}^{-}$ions will undergo hydrolysis to form weak undissociated acid $\mathrm{HCN}$. The system involves simultaneous equilibria.

$$\begin{array}{rl}& \mathrm{AgCN}\rightleftharpoons {\mathrm{Ag}}^{+}+{\mathrm{CN}}^{-}\\ & xx\\ & {\mathrm{H}}^{+}+{\mathrm{CN}}^{-}\to \mathrm{HCN}\\ & {10}^{-2}x-\\ & {10}^{-2}-x-x\\ & \mathrm{HCN}\iff {\mathrm{H}}^{+}+{\mathrm{CN}}^{-}\\ & x{10}^{-2}\\ & x-y{10}^{-2}+yy\end{array}$$

Here,

$$\begin{array}{}\text{(i)}& \begin{array}{ll}& {\mathrm{K}}_{\mathrm{sp}}(\mathrm{AgCN})=\left[{\mathrm{Ag}}^{+}\right]\left[{\mathrm{CN}}^{-}\right]\\ \text{or }& 2.0\times {10}^{-16}=\mathrm{xy}\end{array}\end{array}$$

Also,

$$\begin{array}{rl}{\mathrm{K}}_{\mathrm{a}}(\mathrm{HCN})& =\frac{\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{CN}}^{-}\right]}{[\mathrm{HCN}]}\\ =& \frac{({10}^{-2}+\mathrm{y})\mathrm{y}}{\mathrm{x}-\mathrm{y}}\end{array}$$

Assuming ${10}^{-2}+\mathrm{y}={10}^{-2}$

$6.0\times {10}^{-10}=\frac{{10}^{-2}y}{x-y}$………(ii)

On solving (i) and (ii) we get

$x=5.78\times {10}^{-5}\mathrm{M}$

PRACTICE QUESTIONS

1. If equal volumes of ${\mathrm{BaCl}}_2$ and $\mathrm{NaF}$ solutions are mixed, which of these combination will not give a precipitate?

${\mathrm{K}}_{\mathrm{sp}}$ of ${\mathrm{BaF}}_2=1.7\times {10}^{-7}$

(a) $0.0010\mathrm{M}{\mathrm{BaCl}}_2$ and $0.020\mathrm{M}\mathrm{NaF}$

(b) $0.0010\mathrm{M}{\mathrm{BaCl}}_2$ and $0.015\mathrm{M}\mathrm{NaF}$

(c) $0.0015\mathrm{M}{\mathrm{BaCl}}_2$ and $0.010\mathrm{M}\mathrm{NaF}$

(d) $0.0020\mathrm{M}{\mathrm{BaCl}}_2$ and $0.020\mathrm{M}\mathrm{NaF}$

Show Answer

Answer: (a)

2. The solubility of solid silver chromate, ${\mathrm{Ag}}_2{\mathrm{CrO}}_4$ is determined in three solvents.

${\mathrm{K}}_{\mathrm{sp}}$ of ${\mathrm{Ag}}_2{\mathrm{CrO}}_4=9\times {10}^{-12}$

I. pure water

II. $0.1\mathrm{M}{\mathrm{AgNO}}_3$

III. $0.1\mathrm{M}{\mathrm{Na}}_2{\mathrm{CrO}}_4$

Predict the relative solubility of ${\mathrm{Ag}}_2{\mathrm{CrO}}_4$ in the three solvents :

(a) $\mathrm{I}=\mathrm{II}=\mathrm{III}$

(b) $|<|l\mid$ II

(c) $|=|I|<1$

(d) $\mid l<$ II $<$ l

Show Answer

Answer: (d)

3. The solubility products of $\mathrm{Al}(\mathrm{OH}{)}_3$ and $\mathrm{Zn}(\mathrm{OH}{)}_2$ are $8.5\times {10}^{-23}$ and $1.8\times {10}^{-14}$, respectively. If ${\mathrm{NH}}_4\mathrm{OH}$ is added to a solution containing ${\mathrm{Al}}^{+3}$ and ${\mathrm{Zn}}^{+2}$ ions, then substance precipitated first is :

(a) $\mathrm{Al}(\mathrm{OH}{)}_3$

(b) $\mathrm{Zn}(\mathrm{OH}{)}_2$

(c) Both together

(d) None of these

Show Answer

Answer: (a)

4. If ${\mathrm{K}}_{\mathrm{sp}}\left({\mathrm{PbSO}}_4\right)=1.8\times {10}^{-8}$ and ${\mathrm{K}}_{\mathrm{a}}\left({\mathrm{HSO}}_4^{-}\right)=1.0\times {10}^{-2}$ the equilibrium constant for the reaction : ${\mathrm{PbSO}}_4(\mathrm{s})+{\mathrm{H}}^{+}(\mathrm{aq})\rightleftharpoons {\mathrm{HSO}}_4^{-}(\mathrm{aq})+{\mathrm{Pb}}^{2+}(\mathrm{aq})$ is :

(a) $1.8\times {10}^{-6}$

(b) $1.8\times {10}^{-10}$

(c) $2.8\times {10}^{-10}$

(d) $1.8\times {10}^{-2}$

Show Answer

Answer: (a)

5. ${\mathrm{Ca}}_3{\left({\mathrm{PO}}_4\right)}_2$ is insoluble in water. On adding a few drops of $\mathrm{HCl}$ to solid ${\mathrm{Ca}}_3{\left({\mathrm{PO}}_4\right)}_2$ in contact with water, the solid dissolves. What is the reason?

(a) The solvent becomes more polar on adding $\mathrm{HCl}$

(b) ${\mathrm{Ca}}^{2+}$ ions combine with ${\mathrm{Cl}}^2$ ions

(c) $\mathrm{Ca}{\left({\mathrm{H}}_2{\mathrm{PO}}_4\right)}_2$ is formed, which dissolves

(d) ${\mathrm{H}}_3{\mathrm{PO}}_4$ a weak acid is formed and the ionic product of calcium phosphate drops

Show Answer

Answer: (d)

6. Why does only ${\mathrm{As}}^{3+}$ get precipitated as ${\mathrm{As}}_2{\mathrm{S}}_3$ and not ${\mathrm{Zn}}^{2+}$ as $\mathrm{ZnS}$ when ${\mathrm{H}}_2\mathrm{S}$ is passed through an acidic solution containing ${\mathrm{As}}^{3+}$ and ${\mathrm{Zn}}^{2+}$ ?

(a) The solubility product of ${\mathrm{As}}_2{\mathrm{S}}_3$ less than that of $\mathrm{ZnS}$

(b) Enough ${\mathrm{As}}^{3+}$ ions are present in an acidic medium

(c) Azinc salt does notionize in an acidic medium

(d) The solubility product changes

Show Answer

Answer: (a)

7. When $\mathrm{HCl}(\mathrm{s})$ is passed through a saturated solution of common salt, pure $\mathrm{NaCl}$ is precipitated because:

(a) $\mathrm{HCl}$ is highly soluble in water

(b) The ionic product $\left[{\mathrm{Na}}^{+}\right]\left[{\mathrm{Cl}}^{-}\right]$exceeds its solubility product $\left({\mathrm{K}}_{\mathrm{sp}}\right)$

(c) The ${\mathrm{K}}_{\mathrm{sp}}$ of $\mathrm{NaCl}$ is lowered by the presence of ${\mathrm{Cl}}^{-}$ions

(d) The ionic product $\left({\mathrm{K}}_{\mathrm{p}}\right)\left[{\mathrm{Na}}^{+}\right][\mathrm{Cl}]$ is less than its solubility product $\left({\mathrm{K}}_{\mathrm{sp}}\right)$

Show Answer

Answer: (b)

8. Excess ${\mathrm{Ag}}_2{\mathrm{SO}}_4(\mathrm{s})$. ${\mathrm{BaSO}}_4(\mathrm{s})$ and ${\mathrm{Ba}}_3{\left({\mathrm{PO}}_4\right)}_2(\mathrm{s})$ are simultaneously in equilibrium with distilled water. Which of the following is (are) true? Assume no hydrolysis of dissolved ions.

(a) $\left[{\mathrm{Ag}}^{+}\right]+2\left[{\mathrm{Ba}}^{2+}\right]=2\left[{\mathrm{SO}}_4^{2-}\right]+3\left[{\mathrm{PO}}_4^{3-}\right]$

(b) $2\left[{\mathrm{Ag}}^{+}\right]+4\left[{\mathrm{Ba}}^{2+}\right]=2\left[{\mathrm{SO}}_4^{2-}\right]+2\left[{\mathrm{PO}}_4^{3-}\right]$

(c) $2\left[{\mathrm{Ag}}^{+}\right]+3\left[{\mathrm{Ba}}^{2+}\right]=2\left[{\mathrm{SO}}_4^2\right]+2\left[{\mathrm{PO}}_4^{3-}\right]$

(d) $\left[{\mathrm{Ag}}^{+}\right]+\left[{\mathrm{Ba}}^{2+}\right]=\left[{\mathrm{SO}}_4^{2-}\right]+\left[{\mathrm{PO}}_4^3\right]$

Show Answer

Answer: (b)

9. A solution is found to contain $\left[{\mathrm{Cl}}^{-}\right]=1.5\times {10}^{-1}\mathrm{M};\left[{\mathrm{Br}}^{-}\right]=5.0\times {10}^{-4}\mathrm{M};\left[{\mathrm{CrO}}_4{}^{2-}\right]=1.9\times {10}^{-2}\mathrm{M}$. A solution of ${\mathrm{AgNO}}_3$ ( $100$ dissociated) is added to the above solution drop by drop. Which silver salt will precipitate first?

Given: ${\mathrm{K}}_{\mathrm{sp}}(\mathrm{AgCl})={1.510}^{-10},{\mathrm{K}}_{\mathrm{sp}}(\mathrm{AgBr})=5.0\times {10}^{-13},{\mathrm{K}}_{\mathrm{sp}}\left({\mathrm{Ag}}_2{\mathrm{CrO}}_4\right)=1.9\times {10}^{-12}$

(a) $\mathrm{AgCl}$

(b) $\mathrm{AgBr}$

(c) ${\mathrm{Ag}}_2{\mathrm{CrO}}_4$

(d) $\mathrm{AgCl}$ and $\mathrm{AgBr}$ together

Show Answer

Answer: (b)

10. A saturated solution of ${\mathrm{Ag}}_2{\mathrm{SO}}_4$ has solubility $2.5\times {10}^{-2}\mathrm{M}$. The value of its solubility product is

(a) $62.5\times {10}^{-6}$

(b) $6.25\times {10}^{-4}$

(c) $15.625\times {10}^{-10}$

(d) $3.125\times {10}^{-6}$

Show Answer

Answer: (c)

11. The solubility of ${\mathrm{CaF}}_2$ is $2\times {10}^{-4}\mathrm{mol}/$ litre. Its solubility product is

(a) $2.0\times {10}^{-4}$

(b) $4.0\times {10}^{-8}$

(c) $4\times 8.0\times {10}^{-12}$

(d) $3.2\times {10}^{-4}$

Read the passage and answer the questions given below :

In qualitative analysis, cations of group II as well as group IV both are precipitated in the form of sulphides. Due to low value of ${\mathrm{K}}_{\mathrm{sp}}$ of group II sulphides, group reagent is ${\mathrm{H}}_2\mathrm{S}$ in the presence of dil. $\mathrm{HCl}$ and due to high value of ${\mathrm{K}}_{\mathrm{sp}}$ of group IV sulphides, group reagent is ${\mathrm{H}}_2\mathrm{S}$ in the presence of ${\mathrm{NH}}_4\mathrm{OH}$ and ${\mathrm{NH}}_4\mathrm{Cl}$.

In the solution containing $0.1\mathrm{M}$ each of ${\mathrm{Sn}}^{2+},{\mathrm{Cd}}^{2+}$ and ${\mathrm{Ni}}^{2+}$ ions, ${\mathrm{H}}_2\mathrm{S}$ gas is passed…..

${\mathrm{K}}_{\mathrm{sp}}$ of $\mathrm{SnS}=8\times {10}^{-29}{\mathrm{K}}_{\mathrm{sp}}$ of $\mathrm{CdS}=1\times {10}^{-28},{\mathrm{K}}_{\mathrm{sp}}$ of $\mathrm{NiS}=3\times {10}^{-21}$

${\mathrm{K}}_1$ of ${\mathrm{H}}_2\mathrm{S}=1\times {10}^{-7},{\mathrm{K}}_2$ of ${\mathrm{H}}_2\mathrm{S}=1\times {10}^{-14}$

Show Answer

Answer: (c)

12. If ${\mathrm{H}}_2\mathrm{S}$ is passed into the above mixture in the presence of $\mathrm{HCl}$, which ion will be precipitated first?

(a) $\mathrm{SnS}$

(b) CdS

(c) $\mathrm{NiS}$

(d) SnS & CdS (both together)

Show Answer

Answer: (a)

13. At what value of $\mathrm{pH}$, NiS will start to precipitate?

(a) $12.76$

(b) 7

(c) $1.24$

(d) 4

Show Answer

Answer: (c)

14. Which of the following sulphide is more soluble in pure water?

(a) $\mathrm{CdS}$

(b) NiS

(c) $\mathrm{SnS}$

(d) Equal solubility for all

Show Answer

Answer: (b)

15. If $0.1\mathrm{M}\mathrm{HCl}$ is mixed in the solution containing only $0.1\mathrm{M}{\mathrm{Cd}}^{2+}$ ios and saturated with ${\mathrm{H}}_2\mathrm{S}$. Then $\left[{\mathrm{Cd}}^{24}\right]$ remaining in the solution after CdS stops to precipitate is:

(a) $8.2\times {10}^{-8}$

(b) $8.2\times {10}^{-9}$

(c) $5.6\times {10}^{-7}$

(d) $5.6\times {10}^{-8}$

Show Answer

Answer: (a)