Chemical reactions can be classified as reversible and irreversible reactions. The reactions which occur in one direction i.e. forward direction such that reactants are completely converted into products are called irreversible reactions.

e.g. (i) reaction between equimolar amounts of barium chloride and sodium sulphate resulting in the formation of barium sulphate.

$$ \mathrm{BaCl} _{2}+\mathrm{Na} _{2} \mathrm{SO} _{4} \rightarrow \mathrm{BaSO} _{4}+2 \mathrm{NaCl} $$

(ii) neutralization reaction

$$ \mathrm{H} _{2} \mathrm{SO} _{4}+2 \mathrm{NaOH} \rightarrow \mathrm{Na} _{2} \mathrm{SO} _{4}+2 \mathrm{H} _{2} \mathrm{O} $$

The reactions which can occur in both the directions i.e. forward and backward directions, under similar conditions are called reversible reactions.

e.g. (i) when hydrogen gas is passed over heated iron oxide, iron and water are produced.

$$ \mathrm{Fe} _{3} \mathrm{O} _{4}+4 \mathrm{H} _{2} \rightarrow 3 \mathrm{Fe}+4 \mathrm{H} _{2} \mathrm{O} $$

On the other hand if steam is passed over powdered iron at the same temperature, oxide of iron and hydrogen are formed.

$$ 3 \mathrm{Fe}+4 \mathrm{H} _{2} \mathrm{O} \rightarrow \mathrm{Fe} _{3} \mathrm{O} _{4}+4 \mathrm{H} _{2} $$

When the reaction is carried out in a closed vessel, both reactions can take place in the vessel.

Thus, reactions which proceed in both the directions and donot reach to completion stage are called reversible reactions.

$$ 3 \mathrm{Fe}+4 \mathrm{H} _{2} \mathrm{O} \rightleftharpoons \mathrm{Fe} _{3} \mathrm{O} _{4}+4 \mathrm{H} _{2} $$

The characteristic property of a reversible reaction is that it always attains a state of chemical equilibrium. It is defined as “The state in which the measurable properties of the system such as pressure, density, colour, concentration do not undergo any change with time under given set of conditions”.

At equilibrium, the rate of the forward reaction is exactly equal to the rate of the backward reaction. In this state, the concentrations of reactants and products attain a constant value. This state will continue indefinitely if the conditions such as temperature and concentration are not changed.

The study of chemical equilibrium helps in the elucidation of the optimum conditions for greater yields of the product.

Characteristics of Equilibrium State

(i) It is achieved in a closed system only.

(ii) It is dynamic, can be attained from either side i.e. from the side of reactants or products. (Fig. 1)

$$ \mathrm{R} \rightleftharpoons \mathrm{P} $$

$\qquad$ Fig. 1 : Dynamic Equilibrium

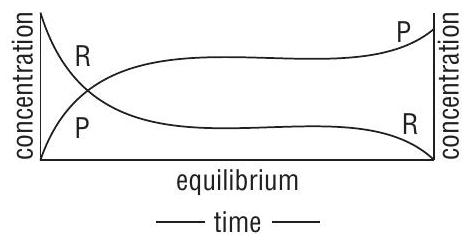
(iii) A catalyst cannot alter the state of equilibrium. It simply helps to attain equilibrium quickly.

Types of chemical equilibria

1. Homogeneous equilibria, i.e., when all the reactants and products are present in the same phase (all gaseous or all liquids). Gaseous reactions are of two types :

$\quad$ i. In which $\mathrm{n} _{\mathrm{p}}=\mathrm{n} _{\mathrm{r}}$, e.g., $\mathrm{N} _{2}(\mathrm{~g})+\mathrm{O} _{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g})$

$\quad$ ii. In which $\mathrm{n} _{\mathrm{p}} \neq \mathrm{n} _{\mathrm{r}}$, e.g., $\mathrm{N} _{2}(\mathrm{~g})+3 \mathrm{H} _{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH} _{3}(\mathrm{~g})$

2. Heterogeneous equilibria, i.e., when all the reactants and products are not in the same phase, e.g.,

$\quad \mathrm{CaCO} _{3}(\mathrm{~s}) \rightleftharpoons \mathrm{CaO}(\mathrm{s})+\mathrm{CO} _{2}(\mathrm{~g})$

The Law of Chemical equilibrium

Application of Law of Mass Action

Consider a reversible homogeneous reaction at equilibrium state.

$\quad a A+b B \rightleftharpoons c C+d D$

Let the active masses of $A, B, C, D$ be $[A],[B],[C]$ and [D] respectively.

Active Mass

(i) For solution and gases active mass is the molar concentration.

(ii) For solids and pure liquids, active mass is unity.

$$ K _{c}=\frac{[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}} $$

$\mathrm{K} _{\mathrm{c}}$ is known as equilibrium constant. It has a definite value for every chemical reaction at a given temperature regardless of concentration of reactants.

Equilibrium constant can also be expressed in terms of partial pressure $\left(\mathrm{K} _{\mathrm{p}}\right)$ or mole fraction $\left(\mathrm{K} _{\mathrm{x}}\right)$

For gas phase reactions

$$ K _{p}=\frac{p _{c}{ }^{c} p _{D}{ }^{d}}{p _{A}{ }^{a} p _{B}^{b}} $$

Relation between $\mathrm{K} _{\mathrm{p}}$ and $\mathrm{K} _{\mathrm{c}}$

$$ \begin{gathered} K _{p}=K _{c}(R T)^{\Delta n} \text { where } \Delta n=\left(n _{p}-n _{r}\right) \text { for gaseous species } \\ \text { If } \Delta n=0, K _{p}=K _{c} \\ \text { If } \Delta n=+v e, K _{p}>K _{c} \\ \text { If } \Delta n=-v e, K _{p}<K _{c} \end{gathered} $$

Equilibrium constant can also be expressed in terms of mole fraction, $x$

$$ K _{x}=\frac{x _{C}^{c} \cdot x _{D}^{d}}{X _{A}^{a} \cdot x _{B}^{b}} $$

Relation between $\mathrm{K} _{\mathrm{p}}$ and $\mathrm{K} _{\mathrm{x}}$

When concentration are expressed in terms of mole fractions

We know that partial pressure $(p)=$ Mole fraction $\times$ Total pressure $(P)$

For the gas phase reaction, $a A+b B \rightleftharpoons c C+d D$

$$ \begin{aligned} p _{A} & =x _{A} P ; p _{B}=x _{B} P \\ p _{c} & =x _{C} P ; p _{D}=x _{D} P \\ K _{p} & =\frac{P _{C}^{c} \cdot P _{D}^{d}}{P _{A}{ }^{a} P _{B}^{b}}=\frac{\left(x _{C} P\right)^{c}\left(x _{D} P\right)^{d}}{\left(x _{A} P\right)^{a}\left(x _{B} P\right)^{b}}=\frac{x _{C}^{c} x _{D}^{d}}{x _{A}{ }^{a} x _{B}^{b}} \times \frac{P^{(c+d)}}{P^{(a+b)}} \\ & =K _{x} P^{(c+d)-(a+b)}=K _{x} P^{\Delta n} \end{aligned} $$

Characteristics of equilibrium constant.

$\quad$ i. Equilibrium constant of a reaction is constant at constant temperature and does not depend upon the concentrations of reactants.

$\quad$ ii. If reaction is reversed, equilibrium constant is inversed, e.g., if it is $\mathrm{K}$ for $\mathrm{A}+\mathrm{B} \rightleftharpoons \mathrm{C}+\mathrm{D}$, then for $\mathrm{C}+\mathrm{D} \rightleftharpoons \mathrm{A}+\mathrm{B}$, $\qquad$ it is $1 / \mathrm{K}$.

$\quad$ iii. If equation with equilibrium constant $\mathrm{K}$ is divided by 2 , the new equilibrium constant is $\sqrt{\mathrm{K}}$.

$\quad$ iv. If equation with equilibrium constant $\mathrm{K}$ is multiplied by 2 , equilibrium constant for the new equation will be $\mathrm{K}^{2}$.

$\quad$ v. If the reaction with equilibrium constant $\mathrm{K}$ takes place in two steps having equilibrium constants $\mathrm{K} _{1}$ and $\mathrm{K} _{2}$, then $\qquad \mathrm{K}=\mathrm{K} _{1} \times \mathrm{K} _{2}$.

$\qquad$ vi. Value of equilibrium constant is not affected by presence of catalyst.

Units of equilibrium constant

$\quad \mathrm{K} _{\mathrm{c}}=\left(\mathrm{molL} \mathrm{L}^{-1}\right)^{\mathrm{an}}$

$\quad \mathrm{K} _{\mathrm{p}}=(\mathrm{atm})^{\Delta n}$ or $(\mathrm{bar})^{\Delta n}$

$\quad \Delta \mathrm{n}=\left(\mathrm{n} _{\mathrm{p}}-\mathrm{n} _{\mathrm{r}}\right)$ gaseous

Effect of temperature

$\quad \log \frac{K _{2}}{K _{1}}=\frac{\Delta H}{2.303 R}\left[\frac{1}{T _{1}}-\frac{1}{T _{2}}\right]$

where $\mathrm{K} _{1}$ and $\mathrm{K} _{2}$ are the equilibrium constants at temperatures $\mathrm{T} _{1}$ and $\mathrm{T} _{2}$ respectively, $\Delta \mathrm{H}$ is the enthalpy of the reaction and $R$ is the gas constant.

For

$\quad \Delta \mathrm{H}=0$, equilibrium constant remains same at all temperatures.

$\quad \Delta \mathrm{H}=(+) v e$, the value of equilibrium constant is higher at higher temperatures.

$\quad \Delta \mathrm{H}=(-)$ ve, the value of equilibrium constant is lower at higher temperatures.

Reaction Quotient-Predicting the direction of the Reaction

Reaction Quotient may be defined as :

The ratio of molar concentrations or the partial pressures of the product species to that of the reacting species at any stage in the reaction, each term being raised to the power equal to its stoichiometric coefficient.

If molar concentration of the species are considered, the reaction quotient is called concentration quotient $\left(Q _{c}\right)$. It is known as partial pressure quotient $\left(Q _{p}\right)$ in case the partial pressures of the different species are considered.

For a reversible reaction, $\mathrm{aA}+\mathrm{bB} \rightleftharpoons \mathrm{cC}+\mathrm{dD}$

Normally reaction quotient is indicated as $Q$ and equilibrium constant as $K$. Predicting the direction of the reaction based on relative values of $Q$ and $K$.

It may be noted that if $Q=K$, the reaction is in a state of equilibrium and in case $Q \neq K$, the reaction is not in a state of equilibrium. Depending upon the conditions, $Q$ and $K$ may be related to each other as:

(i) If $Q=K$, then the reaction is in a state of equilibrium.

(ii) If $Q>K$, then the products are present in large amount as compared to their equilibrium concentrations therefore, the net reaction will proceed in the backward direction to attain equilibrium.

(iii) If $\mathrm{Q}<\mathrm{K}$, then the products are present in smaller amount as compared to their equilibrium concentrations. The net reaction will proceed in the forward direction to attain equilibrium.

Question:1 Consider a reaction

$\mathrm{A}(\mathrm{g})+2 \mathrm{~B}(\mathrm{~g}) \rightarrow \mathrm{C}(\mathrm{g})$

At what pressure, $50 %$ of $\mathrm{A}$ is converted into product when 1 mole of $\mathrm{A}$ is mixed with 2 moles of

B. Given that the temperature of the system is $400 \mathrm{~K}$ and the value of $\mathrm{K} _{\mathrm{c}}=0.35$.

Question:2 Consider the equilibrium $\mathrm{A}(\mathrm{g})+2 \mathrm{~B}(\mathrm{~g}) \rightarrow \mathrm{C}(\mathrm{g})$

At a certain temperature, the equilibrium concentrations of $A$ and $B$ are $2 M$ and $3 M$ respectively. When the volume of the vessel is doubled, the equilibrium is reestablished, the concentration of $B$ is found to be $2 \mathrm{M}$. Calculate $\mathrm{K} _{\mathrm{c}}$ and concentration of ’ $\mathrm{C}$ ’ at two equilibrium stages.

Activation Energies for forward and Backward reactions

In a reversible reaction, both reactions follow the same path and form the same activated complex but their activation energies are different.

$\Delta H=E _{a}(f)-E _{a}(b)$

For exothermic reactions, $\Delta \mathrm{E}$ is negative

For endothermic reaction, $\Delta \mathrm{E}$ is positive

Standard Gibbs energy change of a reaction and its equilibrium constant

Let $\Delta G^{0}$ be the change in Gibbs energy during the reaction when all the reactants and products are in the standard state ( 1 bar) and $\mathrm{K} _{\mathrm{p}}$ be the thermodynamic equilibrium constant of the reaction. Both are related to each other at temperature $T$ by the following relation:

$\Delta G^{0}=-2.303 R T \log K _{p}$

This equation represents one of the most important results of thermodynamics and relates the equilibrium constant of a reaction to a thermochemical property. It is sometimes easier to calculate the Gibbs energy in a reaction rather than to measure the equilibrium constant.

Standard Gibbs energy change can be thermodynamically calculated as :

$$ \Delta \mathrm{G}^{0}=\Delta \mathrm{H}^{0}-\mathrm{T} \Delta \mathrm{S}^{0} $$

Here $\Delta \mathrm{H}^{\circ}=$ standard enthalpy change

$\Delta \mathrm{S}^{0}=$ standard entropy change

(i) When $\Delta G^{0}=0$, then $K _{p}=1$

(ii) When $\Delta G^{0}>0$, i.e., $+v e$, then $K _{p}<1$. In this case, reverse reaction is feasible, i.e., less concentration of products at equilibrium state.

(iii) When $\Delta G^{0}<0$, i.e., $-v e$, then $K _{p}>1$. In this case forward reaction is feasible thereby producing thereby a large concentrations of products till the equilibrium is reached.

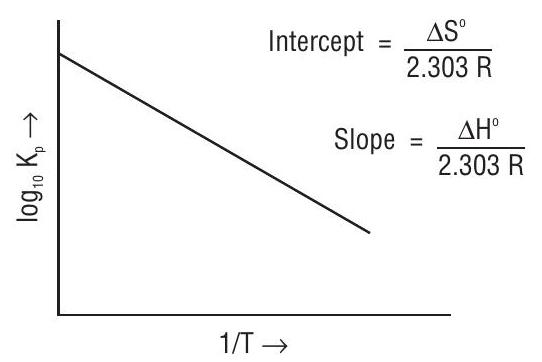
Fig : Variation of Equilibrium constant with inverse of temperature

Question:3 Calculate $\mathrm{K} _{\mathrm{p}}$ and $\mathrm{K} _{\mathrm{c}}$ for the reaction

$\mathrm{CO}(\mathrm{g})+2 \mathrm{H} _{2}(\mathrm{~g}) \rightleftharpoons \mathrm{CH} _{3} \mathrm{OH}(\mathrm{g})$

When hydrogen gas is introduced in a $10 \mathrm{~L}$ flask at $300^{\circ} \mathrm{C}$ containing 0.2 mole of $\mathrm{CO}(\mathrm{g})$ and a catalyst until a pressure of $5 \mathrm{~atm}$ is attained and when equilibrium is reached 0.1 mole of $\mathrm{CH} _{3} \mathrm{OH}(\mathrm{g})$ is formed.

Question:4 At $55^{\circ} \mathrm{C}$ and $1 \mathrm{~atm}, 50.3 %$ of $\mathrm{N} _{2} \mathrm{O} _{4}$ decomposes as per the following reaction

$\mathrm{N} _{2} \mathrm{O} _{4}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO} _{2}(\mathrm{~g})$

At what pressure, the equilibrium mixture has the amounts of $\mathrm{NO} _{2}$ and $\mathrm{N} _{2} \mathrm{O} _{4}$ in the ratio $1: 10$

LE CHATELIER’SPRINCIPLE

If a system, at equilibrium, is subjected to a change of concentration, pressure or temperature, the equilibrium shifts in the direction that tends to undo the effect of the change.

This leads to the following important results:

(i) An increase in concentration of reactants always favours forward reaction so as to reduce the amount of reactants.

(ii) An increase in concentration of products always favours backward reaction so as to reduce the amount of products.

(iii) An increase in pressure always favours the reaction where the number of gaseous molecules is reduced.

(iv) A rise in temperature favours the endothermic reaction

Effect of addition of inert gas

Applications of Le Chatelier’s Principle

1. Physical equilibrium

(a) Ice-water system (Melting of ice):

The change can be represented as

Ice + Heat $\rightleftharpoons$ Water

In this change, heat is absorbed (endothermic) and there is decrease in volume. According to Le Chatelier’s principle, the favourable conditions for the melting of ice are :

(i) High pressure and

(ii) Hightemperature

(b) Water-water vapour system (Vaporisation of water)

The change can be represented as:

Water + Heat $\rightleftharpoons$ Water vapour

This change is endothermic (heat is absorbed) and there is increase in volume. Thus, favourable conditions for the conversion of water into water vapour are:

(i) High temperature and

(ii) Low pressure

(c) Effect of pressure on solubility of gases

Gas + Solvent $\rightleftharpoons$ Solution (and $\mathrm{V} _{\mathrm{f}}>\mathrm{V} _{\mathrm{b}}$ )

where $V _{t}$ is volume of left hand side components and $V _{b}$ is volume of right hand side components. An increase in pressure will favour forward reaction and thus solubility of gas increases with increase in pressure.

(d) Effect of temperature on solubility of solids

Solute + Solvent $\rightleftharpoons$ Solution, $\Delta \mathrm{H}=+v \mathrm{e}$

An increase in temperature always favours endothermic process and thus, solute having endothermic dissolution (e.g., urea, glucose) show an increase in their solubility with temperature

Solute + Solvent $\rightleftharpoons$ Solution, $\Delta \mathrm{H}=-\mathrm{ve}$

Accordingly, solute having exothermic dissolution (e.g., lime, acids) show a decrease in their solubility with temperature.

Note: (i) Hydrated salts like $\mathrm{CuSO} _{4} \bullet 5 \mathrm{H} _{2} \mathrm{O}, \mathrm{CaCl} _{2} \bullet 6 \mathrm{H} _{2} \mathrm{O}$ etc. dissolve in water generally with absorption of heat.

$\qquad$ (ii) Solubility of $\mathrm{NaOH}$ increases with temperature although dissolution is exothermic.

2. For chemical equilibrium

(a) Formation of ammonia

$\mathrm{N} _{2}+3 \mathrm{H} _{2} \rightleftharpoons 2 \mathrm{NH} _{3} \Delta \mathrm{H}=-\mathrm{ve}$

The increase in pressure favours forward reaction,

The increase in temperature favours backward reaction.

The increase in concentration of reactant(s) favours forward reaction.

The increase in concentration of product favours backward reaction. Thus, to get better yield of $\mathrm{NH} _{3}$, one must keep :

(a) High pressure

(b) Low temperature

(c) High concentration of reactants

(d) $\mathrm{NH} _{3}$, formed should be taken out as soon as it is formed in order to have low concentration of $\mathrm{NH} _{3}$, in equilibrium. This can be done by passing a stream of water through equilibrium mixture.

(b) Formation of $\mathrm{HI}$

$\mathrm{H} _{2}(\mathrm{~g})+\mathrm{I} _{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{H}(\mathrm{g})+3000$ cal

Effect of concentration

When concentration of $\mathrm{H} _{2}$ or $\mathrm{I} _{2}$ is increased at equilibrium, the system moves in a direction which decreases the concentration, i.e. the rate of forward reaction increases thereby increasing the concentration of $\mathrm{HI}$.

Effect of pressure

As there is no change in the number of moles in the reaction, the equilibrium state remains unaffected by change of pressure.

Effect of temperature

By increasing temperature the equilibrium state shift towards the reaction which moves with absorption of heat. The formation of $\mathrm{HI}$ is an exothermic reaction. Thus, the backward reaction moves faster when temperature is increased.

In short, we can say that the favourable conditions for greater yield of $\mathrm{HI}$ are:

(i) High concentrations of $\mathrm{H} _{2}$ and $\mathrm{I} _{2}$ and

(ii) Lowtemperature

Relation between vapour density and degree of dissociation

In case of reversible reactions, degree of dissociation is determined by measuring density of reaction mixture at equilibrium. Consider a general reaction

$A \rightleftharpoons n B$

Initial no of moles $\qquad \qquad \qquad 1 \qquad 0 $

No. of moles at equilibrium $\qquad 1-x \quad n x $

Total no. of moles $\quad \qquad \qquad = 1-x + n x$

$\therefore$ Volume at equilibrium $\qquad = 1+x(n-1)] \text { V litres }$

Let the initial volume be $\mathrm{V}$ litres. Let ’ $\mathrm{D}$ ’ be the vapour density when there is no dissociation and ’ $d$ ’ be the vapour density when degree of dissociation is ’ $x$ ‘.

$$ \begin{aligned} & \Rightarrow \quad D \propto \frac{1}{V} \quad \text { and } \quad d \propto \frac{1}{[1+(n-1) x] V} \\ & \qquad \frac{D}{d}=[1+(n-1) x] \\ & \Rightarrow \quad x=\frac{D-d}{(n-1) d} \\ & \text { or } \quad x=\frac{M-m}{(n-1) m} \end{aligned} $$

where $\mathrm{n}=$ number of gas molecules produced by 1 molecule of the reactant.

$\mathrm{M}=$ molar mass of the reactant

and $m=$ apparent molar mass of the reactant after dissociation.

Question. 5 What is the percentage dissociation of $\mathrm{N} _{2} \mathrm{O} _{4}$ at $350^{\circ} \mathrm{C}$ if the observed molar mass of $\mathrm{N} _{2} \mathrm{O} _{4}$ at $350^{\circ} \mathrm{C}$ is $80 \mathrm{~g} / \mathrm{mol}$.

Question. 6 $1 \mathrm{~mol}$ of $\mathrm{N} _{2}$ and 2 moles of $\mathrm{PCl} _{5}$ are heated to $100^{\circ} \mathrm{C}$ in a $100 \mathrm{~L}$ container. The pressure at equilibrium is found to be $1.5 \mathrm{~atm}$. Calculate the degree of dissociation of $\mathrm{PCI} _{5}$.

PRACTICE QUESTIONS

1. For the reaction:

$\quad \mathrm{CO}(\mathrm{g})+1 / 2 \mathrm{O} _{2}(\mathrm{~g}) \rightarrow \mathrm{CO} _{2}(\mathrm{~g}) ; \mathrm{K} _{\mathrm{p}} / \mathrm{K} _{\mathrm{c}} \text { is }$

(a) $\quad R T$

(b) $\quad(\mathrm{RT})^{-1}$

(c) $\quad(\mathrm{RT})^{-1 / 2}$

(d) $\quad(\mathrm{RT})^{1 / 2}$

2. For the equilibrium reaction:

$\mathrm{N} _{2} \mathrm{O} _{4}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO} _{2}(\mathrm{~g})$

the concentration of $\mathrm{N} _{2} \mathrm{O} _{4}$ and $\mathrm{NO} _{2}$ at equilibrium are : $4.8 \times 10^{-2}$ and $1.2 \times 10^{-2} \mathrm{~mol} \mathrm{~L}^{-1}$ respectively. The value of $\mathrm{K} _{\mathrm{c}}$ for the reaction is :

(a) $\quad 3 \times 10^{-1} \mathrm{~mol} \mathrm{~L}^{-1}$

(b) $\quad 3 \times 10^{-3} \mathrm{~mol} \mathrm{~L}^{-1}$

(c) $\quad 3 \times 10^{3} \mathrm{~mol} \mathrm{~L}^{-1}$

(d) $\quad 3.3 \times 10^{3} \mathrm{molL}^{-1}$

3. What is the equilibrium expression for the following reaction?

$\mathrm{P} _{4}(\mathrm{~s})+5 \mathrm{O} _{2}(\mathrm{~g}) \rightleftharpoons \mathrm{P} _{4} \mathrm{O} _{10}(\mathrm{~s})$

(a) $\quad \mathrm{K} _{\mathrm{c}}=\left[\mathrm{O} _{2}\right]^{5}$

(b) $\quad \mathrm{K} _{\mathrm{c}}=\left[\mathrm{P} _{4} \mathrm{O} _{10}\right] /\left[\mathrm{P} _{4}\right]\left[\mathrm{O} _{2}\right]^{5}$

(c) $\quad \mathrm{K} _{\mathrm{c}}=\left[\mathrm{P} _{4} \mathrm{O} _{10}\right] / 4\left[\mathrm{P} _{4}\right]\left[\mathrm{O} _{2}\right]$

(d) $\quad \mathrm{K} _{\mathrm{c}}=\frac{1}{\left[\mathrm{O} _{2}\right]^{5}}$

4. The equilibrium constant $\left(\mathrm{K} _{\mathrm{c}}\right)$ for the reaction is $4.9 \times 10^{-2}$

$ \mathrm{SO} _{3}(\mathrm{~g}) \rightleftharpoons \mathrm{SO} _{2}(\mathrm{~g})+1 / 2 \mathrm{O} _{2}(\mathrm{~g})$

The value of $\mathrm{K} _{\mathrm{c}}$ for the reaction

$ 2 \mathrm{SO} _{2}(\mathrm{~g})+\mathrm{O} _{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{SO} _{3}(\mathrm{~g}) \text { is : }$

(a) $\quad $ 416

(b) $\quad 2.4 \times 10^{-3}$

(c) $\quad 9.8 \times 10^{-2}$

(d) $\quad 4.9 \times 10^{-2}$

5. The equilibrium constant $\left(\mathrm{K} _{\mathrm{c}}\right)$ for the reaction $\mathrm{N} _{2}(\mathrm{~g})+\mathrm{O} _{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g})$ at temperature $\mathrm{T}$ is $4 \times 10^{-4}$. The value of $\mathrm{K} _{\mathrm{c}}$ for the reaction, $\mathrm{NO}(\mathrm{g}) \rightleftharpoons \frac{1}{2} \mathrm{~N} _{2}(\mathrm{~g})+\frac{1}{2} \mathrm{O} _{2}(\mathrm{~g})$ at the same temperature is

(a) $\quad 2.5 \times 10^{2}$

(b) $\quad 4 \times 10^{-4}$

(c) $\quad$ 50.0

(d) $\quad$ 0.02

6. For which of the following reaction, $\mathrm{K} _{\mathrm{p}}=\mathrm{K} _{\mathrm{c}}$ ?

(a) $\quad 2 \mathrm{NOCl}(\mathrm{g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g})+\mathrm{Cl} _{2}(\mathrm{~g})$

(b) $\quad \mathrm{N} _{2}(\mathrm{~g})+3 \mathrm{H} _{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH} _{3}(\mathrm{~g})$

(c) $\quad \mathrm{H} _{2}(\mathrm{~g})+\mathrm{Cl} _{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HCl}(\mathrm{g})$

(d) $\quad \mathrm{PCl} _{3}(\mathrm{~g})+\mathrm{Cl} _{2}(\mathrm{~g}) \rightleftharpoons \mathrm{PCl} _{5}(\mathrm{~g})$

7. An equilibrium mixture for the reaction

$\quad 2 \mathrm{H} _{2} \mathrm{~S}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{H} _{2}(\mathrm{~g})+\mathrm{S} _{2}(\mathrm{~g})$

had 1 mole of $\mathrm{H} _{2} \mathrm{~S}, 0.2$ mole of $ _{2}$ and 0.08 mole of $\mathrm{S} _{2}$ in a 2 litre flask. The value of $\mathrm{K} _{\mathrm{c}}$ in mol L $^{-1}$ is

(a) $\quad 0.004$

(b) $\quad 0.08$

(c) $\quad 0.016$

(d) $\quad$ 0.160

8. For the reversible reaction

$ \mathrm{N} _{2}(\mathrm{~g})+3 \mathrm{H} _{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH} _{3}(\mathrm{~g})$

at $500^{\circ} \mathrm{C}$, the value of $\mathrm{K} _{\mathrm{p}}$ is $1.44 \times 10^{-5}$ when partial pressure is measured in atmospheres. The corresponding value of $\mathrm{K} _{\mathrm{c}}$, with concentration in mole litre ${ }^{-1}$ is

(a) $\quad 1.44 \times 10^{-5} /(0.0832 \times 500)^{-2}$

(b) $\quad 1.44 \times 10^{-5} /(8.314 \times 773)^{-2}$

(c) $\quad 1.44 \times 10^{-5} /(0.082 \times 773)^{2}$

(d) $\quad 1.44 \times 10^{-5} /(0.0832 \times 773)^{-2}$

9. At constant temperature, the equilibrium constant $\left(K _{p}\right)$ for the decomposition reaction $\mathrm{N} _{2} \mathrm{O} _{4} \rightleftharpoons 2 \mathrm{NO} _{2}$ is expressed by $K _{p}=\left(4 x^{2} P\right) /\left(1-x^{2}\right)$, where $P=$ pressure, $x=$ extent of decomposition. Which one of the following statements is true?

(a) $K _{p}$ increases with increase of $P$

(b) $K _{p}$ increases with increase of $x$

(c) $K _{p}$ increases with decrease of $x$

(d) $K _{p}$ remains constant with change in $P$ and $x$.

10. A mixture of $\mathrm{N} _{2}$ and $\mathrm{H} _{2}$ in the molar ratio $1: 3$ attains equilibrium when $50 %$ of the mixture has reacted. If $\mathrm{P}$ is the total pressure of the mixture, then partial pressure of $\mathrm{NH} _{3}$ formed is

(a) $\quad \mathrm{P} / 2$

(b) $\quad P / 3$

(c) $\quad \mathrm{P} / 4$

(d) $\quad P / 6$

11. For the reaction:

$\mathrm{H} _{2}(\mathrm{~g})+\mathrm{CO} _{2}(\mathrm{~g}) \rightleftharpoons \mathrm{CO}(\mathrm{g})+\mathrm{H} _{2} \mathrm{O}(\mathrm{g})$, if the intial pressure of $\left[\mathrm{H} _{2}\right]=\left[\mathrm{CO} _{2}\right]$ and $\mathrm{x}$ moles / litre of hydrogen is consumed at equilibrium, the correct expression of $\mathrm{K} _{\mathrm{p}}$ is

(a) $\quad\frac{x^{2}}{(1-x)^{2}}$

(b) $\quad \frac{(1+x)^{2}}{(1-x)^{2}}$

(c) $\quad\frac{x^{2}}{(2+x)^{2}}$

(d) $\quad\frac{x^{2}}{1-x^{2}}$

12. Consider the following gaseous equilibrium with equilibrium constants $\mathrm{K} _{1}$ and $\mathrm{K} _{2}$ respectively

$ \begin{aligned} & \mathrm{SO} _{2}(\mathrm{~g})+\frac{1}{2} \mathrm{O} _{2}(\mathrm{~g}) \rightleftharpoons \mathrm{SO} _{3}(\mathrm{~g}) \\ & 2 \mathrm{SO} _{3}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{SO} _{2}(\mathrm{~g})+\mathrm{O} _{2}(\mathrm{~g}) \end{aligned}$

The equilibrium constants are related as

(a) $\quad \mathrm{K} _{1}^{2}=\frac{1}{\mathrm{~K} _{2}}$

(b) $\quad 2 \mathrm{~K} _{1}=\mathrm{K} _{2}{ }^{2}$

(c) $\quad \mathrm{K} _{2}=\frac{2}{\mathrm{~K} _{1}{ }^{2}}$

(d) $\quad \mathrm{K} _{2}^{2}=\frac{1}{\mathrm{~K} _{1}}$

13. Consider the following equilibrium in a closed container:

$\mathrm{N} _{2} \mathrm{O} _{4}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO} _{2}(\mathrm{~g})$. At a fixed temperature, the volume of the reaction container is halved. For this change, which of the following statements holds true regarding the equilibrium constant $\left(\mathrm{K} _{\mathrm{p}}\right)$ and degree of dissociation $(\alpha)$ ?

(a) $\quad$ Neither $\mathrm{K} _{\mathrm{p}}$ nor $\alpha$ changes

(b) $\quad$ Both $\mathrm{K} _{\mathrm{p}}$ and $\alpha$ change

(c) $\quad \mathrm{K} _{\mathrm{p}}$ changes but $\alpha$ does not change

(d) $\quad K _{p}$ does not change but $\alpha$ changes

14. Chemical equilibrium is attained in a reversible reaction carried in a close container and is of dynamic nature. The value of equilibrium constant may be expressed either as $\mathrm{K} _{\mathrm{p}}$ and $\mathrm{K} _{\mathrm{c}}$ and the two are related to each other as: $\quad K _{p}=K _{c}(R T)^{\Delta n _{g}}$

Free energy change $(\Delta G)$ at equilibrium point is zero. The value of equilibrium constant gives the extent to which a particular reaction has proceeded to attain the equilibrium. Its value becomes inverse of the initial value if the reaction is reversed and becomes the square root of the initial value if the reaction is divided by 2 .

1. A reaction attains equilibrium when the free energy change accompanying the reaction is:

(a) Positive and large

(b) Zero

(c) Negative

(d) Negative and small

2. The equilibrium constant for the reaction:

$\mathrm{N} _{2}+3 \mathrm{H} _{2} \rightleftharpoons 2 \mathrm{NH} _{3}$ is K

and for the reaction

$1 / 2 \mathrm{~N} _{2}+3 / 2 \mathrm{H} _{2} \rightleftharpoons \mathrm{NH} _{3}$ is $\mathrm{K}^{\prime}$

$\mathrm{K}$ and $\mathrm{K}^{1}$ are related to each other as:

(a) $\mathrm{K}=\mathrm{K}^{\prime}$

(b) $\mathrm{K}^{\prime}=\sqrt{\mathrm{K}}$

(c) $\mathrm{K}=\sqrt{\mathrm{K}^{\prime}}$

(d) $\quad \mathrm{K} \times K^{\prime}=1$

3. For the reaction

$\mathrm{PCl} _{3}+\mathrm{Cl} _{2} \rightleftharpoons \mathrm{PCl} _{5}$

the value of $\mathrm{K} _{\mathrm{c}}$ at $250^{\circ} \mathrm{C}$ is $26 \mathrm{~mol}^{-1} \mathrm{~L}$. The value of $\mathrm{K} _{\mathrm{p}}$ at the same temperature will be:

(a) $\quad 0.61 \mathrm{~atm}^{-1}$

(b) $\quad 0.57 \mathrm{~atm}^{-1}$

(c) $\quad 0.83 \mathrm{~atm}^{-1}$

(d) $\quad 0.46 \mathrm{~atm}^{-1}$

4. When the two reactants $A$ and $B$ are mixed to give products $C$ and $D$, the reaction quotient Q when the reaction begins is

(a) zero

(b) decreases with time

(c) is independent of time

(d) increases with time

PRACTICE QUESTIONS

1. $A$ and $B$ are gaseous substances which react reversibly to give two gaseous substances $C$ and $D$, accompanied by the liberation of heat. When the reaction reaches equilibrium, it is observed that $\mathrm{K} _{\mathrm{p}}=\mathrm{K} _{\mathrm{c}}$. The equilibrium cannot be disturbed by

(a) Adding $\mathrm{A}$

(b) Adding D

(c) Raising the temperature

(d) Increasing the pressure

2. The value of equilibrium constant for an endothermic reaction

(a) increases with increase of temperature

(b) decreases with increase of temperature

(c) is independent of temperature

(d) sufficient information is not available to answer the question

3. A reaction reaches a state of chemical equilibrium only when

(a) the reactants and the products are reacting

(b) the concentrations of the reactants and products become equal

(c) the products react together at the same rate at which they are formed

(d) all the reactants and the products are in the same state of matter.

4. For the gas phase reaction

$2 \mathrm{NO}(\mathrm{g}) \rightleftharpoons \mathrm{N} _{2}(\mathrm{~g})+\mathrm{O} _{2}(\mathrm{~g})+43.5 \mathrm{kcal}$

which one of the statements below is true for

$\mathrm{N} _{2}(\mathrm{~g})+\mathrm{O} _{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g})$

(a) $K$ is independent of $T$

(b) Kincreases as $T$ decreases

(c) Kdecreases as $T$ decreases

(d) Kvaries with the addition of $\mathrm{NO}$

5. According to Le Chatelier’s principle, adding heat to a solid and liquid in equilibrium will cause the

(a) temperature to increase

(b) temperature to decrease

(c) amount of liquid to decrease

(d) amount of solid to decrease

6. For the reaction $2 A+B \rightleftharpoons C ; \Delta H=+x$ cal. Which one of the following conditions would favour the yield of $C$ on the basis of Le Chatelier principle?

(a) High pressure, high temperature

(b) Only low temperature

(c) High pressure, low temperature

(d) Only low pressure

7. For the reaction $\mathrm{PCl} _{5}(\mathrm{~g}) \rightleftharpoons \mathrm{PCl} _{3}(\mathrm{~g})+\mathrm{Cl} _{2}(\mathrm{~g})$ the forward reaction at constant temperature is favoured by

(a) Introducing an inert gas at constant volume

(b) Introducing $\mathrm{PCl} _{3}(\mathrm{~g})$ at constantvolume

(c) Introducing $\mathrm{PCl} _{5}(\mathrm{~g})$ at constant volume

(d) Introducing $\mathrm{Cl} _{2}(\mathrm{~g})$ at constant volume

8. On the basis of Le Chatelier’s principle, predict which of the following conditions would be un-favourable for the formation of $\mathrm{SO} _{3}$ ? Given that

$2 \mathrm{SO} _{2}+\mathrm{O} _{2} \rightleftharpoons 2 \mathrm{SO} _{3} ; \Delta \mathrm{H}=-42 \mathrm{kcal}$

(a) Low pressure

(b) High pressure

(c) Low temperature

(d) High concentration of $\mathrm{SO} _{2}$

9. For the chemical reaction:

$3 \mathrm{X}(\mathrm{g})+\mathrm{Y}(\mathrm{g}) \rightleftharpoons \mathrm{X} _{3} \mathrm{Y}(\mathrm{g})$

the amount of $X _{3} Y$ at equilibrium is affected by

(a) temperature and pressure

(b) pressure only

(c) temperature only

(d) temperature, pressure and catalyst

10. 2.2 moles of phosphorus pentachloride were taken in a closed vessel and dissociated into phosphorus trichloride and chlorine. At equilibrium, the total number of moles of the reactant and the products was 2.53. The degree of dissociation is :

(a) $\quad 0.33$

(b) $\quad 0.165$

(c) $\quad 0.15$

(d) $\quad 0.30$

11. Starting with 1 mole of $\mathrm{N} _{2} \mathrm{O} _{4}$, if ’ $\alpha$ ’ is the degree of dissociation of $\mathrm{N} _{2} \mathrm{O} _{4}$ for the reaction:

$\quad \mathrm{N} _{2} \mathrm{O} _{4} \rightleftharpoons 2 \mathrm{NO} _{2}$

then at equilibrium the total number of moles of $\mathrm{N} _{2} \mathrm{O} _{4}$ and $\mathrm{NO} _{2}$ present is

(a) 2

(b) $1-\alpha$

(c) $(1-\alpha)^{2}$

(d) $1+\alpha$

12. Vapour density of $\mathrm{PCl} _{5}$ is 104.16 but when heated at $230^{\circ} \mathrm{C}$ its vapour density is reduced to 62 . The degree of dissociation of $\mathrm{PCl} _{5}$ at this temperature will be

(a) $6.8 %$

(b) $68 %$

(c) $46 %$

(d) $64 %$

CHEMICAL EQUILIBRIUM ASSIGNMENT - I

OBJECTIVE QUESTIONS

1. An aqueous solutions of hydrogen sulphide shows the equilibrium:

$\quad \mathrm{H} _{2} \mathrm{~S} \rightleftharpoons \mathrm{H}^{+}+\mathrm{HS}^{-}$

If dilute $\mathrm{HCl}$ is added to an aqueous solution of hydrogen sulphide without any change in temperature, then:

a. The equilibrium constant will change

b. The concentration of $\mathrm{HS}^{-}$will increase

c. The concentration of un-dissociated hydrogen sulphide will decrease

d. The concentration of $\mathrm{HS}^{-}$will decrease

2. On applying pressure to the equilibrium: $\quad$ ice $\rightleftharpoons$ water

Which phenomenon will happen?

a. More ice will be formed

b. More water will be formed

c. Equilibrium will not be disturbed

d. Water will evaporate

3. The vapour density of completely dissociated $\mathrm{NH} _{4} \mathrm{Cl}$ would be :

a. Slightly less than half of that of ammonium chloride

b. Half of that of ammonium chloride

c. Double that of ammonium chloride

d. Determined by the amount of solid ammonium chloride used in the experiment

4. Which of the following statements is (are) correct regarding the solubility of a non-reacting gas into a fixed amount of water?

a. The dissolution of gas results in the decrease of temperature

b. The solubility is favoured by high pressure and low temperature

c. The volume of gas dissolved at a fixed temperature and pressure remains constant

d. The amount dissolved increases exponentially with the pressure of the gas

5. If the reaction $\mathrm{N} _{2} \mathrm{O} _{4} \rightleftharpoons 2 \mathrm{NO} _{2}$, is started with one mole of $\mathrm{N} _{2} \mathrm{O} _{4}$ and $\alpha$ is degree of dissociation of $\mathrm{N} _{2} \mathrm{O} _{4}$ then the number of moles at equilibrium will be :

a. 3

b. 1

c. $(1-\alpha)^{2}$

d. $(1+\alpha)$

6. Eight mole of a gas $\mathrm{AB} _{3}$ attain equilibrium in a closed container of volume $1 \mathrm{dm}^{3}$ as, $2 \mathrm{AB} _{3} \rightleftharpoons \mathrm{A} _{2}(\mathrm{~g})+3 \mathrm{~B} _{2}(\mathrm{~g})$. If at equilibrium 2 mole of $\mathrm{A} _{2}$ are present then equilibrium constant is :

a. $\quad 72 \mathrm{~mol}^{2} \mathrm{~L}^{-2}$

b. $\quad 36 \mathrm{~mol}^{2} \mathrm{~L}^{-2}$

c. $\quad 3 \mathrm{~mol}^{2} \mathrm{~L}^{-2}$

d. $\quad 27 \mathrm{~mol}^{2} \mathrm{~L}^{-2}$

7. For the reaction, $\mathrm{CO}(\mathrm{g})+\mathrm{Cl} _{2}(\mathrm{~g}) \rightleftharpoons \mathrm{COCl} _{2}(\mathrm{~g})$ the value of $\mathrm{K} _{\mathrm{p}} / \mathrm{K} _{\mathrm{c}}$ is equal to :

a. $ 1.0$

b. RT

c. RT

d. $\frac{1}{\mathrm{RT}}$

8. A definite amount of solid $\mathrm{NH} _{4} \mathrm{HS}$ is placed in a flask already containing $\mathrm{NH} _{3}$ gas at certain temperature and 0.50 atm pressure. $\mathrm{NH} _{4} \mathrm{HS}$ decomposes to give $\mathrm{NH} _{3}$ and $\mathrm{H} _{2} \mathrm{~S}$ and total equilibrium pressure in flask is $0.84 \mathrm{~atm}$. The equilibrium constant for the reaction is :

a. $ 0.30$

b. $ 0.18$

c. $ 0.17$

d. $ 0.11$

9. For a polyprotic acid say $\mathrm{H} _{3} \mathrm{PO} _{4}$, its three dissociation constant $\mathrm{K} _{1}, \mathrm{~K} _{2}$, and $\mathrm{K} _{3}$ are in the order

a. $\mathrm{K} _{1}<\mathrm{K} _{2}<\mathrm{K} _{3}$

b. $ \mathrm{K} _{1}>\mathrm{K} _{2}>\mathrm{K} _{3}$

c. $ \mathrm{K} _{1}=\mathrm{K} _{2}=\mathrm{K} _{3}$

d. $\mathrm{K} _{1}=\mathrm{K} _{2}>\mathrm{K} _{3}$

10. When a sample of $\mathrm{NO} _{2}$ is placed in a container, this equilibrium is rapidly established. If this equilibrium mixture acquires a darker colour at high temperatures and at low pressure, which of these statements about the reaction is true?

$\quad 2 \mathrm{NO} _{2}(\mathrm{~g}) \rightleftharpoons \mathrm{N} _{2} \mathrm{O} _{4}(\mathrm{~g})$

a. The reaction is exothermic and $\mathrm{N} _{2} \mathrm{O} _{4}$ is darker in colour than $\mathrm{NO} _{2}$

b. The reaction is exothermic and $\mathrm{NO} _{2}$ is darker in colour than $\mathrm{N} _{2} \mathrm{O} _{4}$

c. The reaction is endothermic and $\mathrm{NO} _{2}$ is darker in colour than $\mathrm{N} _{2} \mathrm{O} _{4}$

d. The reaction is endothermic and $\mathrm{N} _{2} \mathrm{O} _{4}$ is darker in colour than $\mathrm{NO} _{2}$

11. For the reaction $\mathrm{CaCO} _{3}(\mathrm{~s}) \rightleftharpoons \mathrm{CaO}(\mathrm{s})+\mathrm{CO} _{2}(\mathrm{~g})$, the pressure of $\mathrm{CO} _{2}(\mathrm{~g})$ depends on

a. the mass of $\mathrm{CaCO} _{3}(\mathrm{~s})$

b. the mass of $\mathrm{CaO}(\mathrm{s})$

c. the masses of both $\mathrm{CaCO} _{3}(\mathrm{~s})$ and $\mathrm{CaO}(\mathrm{s})$

d. temperature of the system

12. For the reaction $\mathrm{N} _{2} \mathrm{O} _{4}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO} _{2}(\mathrm{~g})$, the relation connecting the degree of dissociation $(\alpha)$ of $\mathrm{N} _{2} \mathrm{O} _{4}(\mathrm{~g})$ with the equilibrium constant $\mathrm{K} _{\mathrm{p}}$ is :

a. $\quad \alpha=\frac{\mathrm{K} _{\mathrm{p}} / \mathrm{p}}{4+\mathrm{K} _{\mathrm{p}} / \mathrm{p}}$

b. $\quad \alpha=\frac{K _{p}}{4+K _{p}}$

c. $\quad \alpha=\left(\frac{K _{p} / p}{4+K _{p} / p}\right)^{1 / 2}$

d. $\quad \alpha=\left(\frac{K _{p}}{4+K _{p}}\right)^{1 / 2}$

13. The concentration of a pure solid or liquid phase is not included in the expression of equilibrium constant because

a. solid and liquid concentrations are independent of their quantities

b. solids and liquids react slowly

c. solids and liquids at equilibrium do not interact with gaseous phase

d. the molecules of solids and liquids cannot migrate to the gaseous phase

14. When a bottle of cold drink is opened, the gas come out with a fizz due to

a. decrease in pressure suddenly which results in a decrease in solubility of $\mathrm{CO} _{2}$ gas in water

b. decrease in temperature

c. increase in pressure

d. none of the above

15. Densities of diamond and graphite are 3.5 and $2.3 \mathrm{~g} / \mathrm{mL}$ respectively. Increase of pressure on the equilibrium; $\quad$ Diamond $(s) \rightleftharpoons$ Graphite (s)

a. favours backward reaction

b. favours forward reaction

c. has no effect

d. increases the reaction rate

16. Solubility of a gas in a liquid increases on:

a. addition of catalyst

b. increasing the pressure

c. decreasing the pressure

d. increases the reaction rate

17. For the reaction $\left[\mathrm{Ag}(\mathrm{CN}) _{2}\right]^{-} \rightleftharpoons \mathrm{Ag}^{+}+2 \mathrm{CN}^{-}$, the equilibrium constant $\mathrm{K} _{\mathrm{c}}$, at $25^{\circ} \mathrm{C}$ is $4.0 \times 10^{-19}$ then the silver ion concentration in a solution which was originally 0.1 molar in $\mathrm{KCN}$ and 0.03 molar in $\mathrm{AgNO} _{3}$ is:

a. $\quad 7.5 \times 10^{18}$

b. $\quad 7.5 \times 10^{-18}$

c. $\quad 7.5 \times 10^{19}$

d. $\quad 7.5 \times 10^{-19}$

SUBJECTIVE QUESTIONS

1. $13.8 \mathrm{~g}$ of $\mathrm{N} _{2} \mathrm{O} _{4}$ was placed in $1 \mathrm{~L}$ reaction vessel at $400 \mathrm{~K}$ and allowed to attain eqn : $\mathrm{N} _{2} \mathrm{O} _{4}(\mathrm{~g}) \rightleftharpoons$ $2 \mathrm{NO} _{2}(\mathrm{~g})$. The total pressure at equilibrium was found to be 9.15 bar. Calculate $\mathrm{K} _{\mathrm{c}}, \mathrm{K} _{\mathrm{p}}$ and partial pressures of $\mathrm{N} _{2} \mathrm{O} _{4}$ and $\mathrm{NO} _{2}$ at equilibrium.

2. At temperature $\mathrm{T}$, a compound $\mathrm{AB} _{2}(\mathrm{~g})$ dissociates according to the reaction $2 \mathrm{AB} _{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{AB}(\mathrm{g})+\mathrm{B} _{2}(\mathrm{~g})$ with degree of dissociation as ’ $\alpha$ ’ which is negligibly small as compared to unity. Deduce the expression for ’ $\alpha$ ’ in terms of equilibrium constant $\mathrm{K} _{\mathrm{p}}$ and total pressure $\mathrm{P}$.

3. A sample of air consisting of $\mathrm{N} _{2}$ and $\mathrm{O} _{2}$ was heated to $2500 \mathrm{~K}$ until the equilibrium

$\mathrm{N} _{2}(\mathrm{~g})+\mathrm{O} _{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g})$

was established with an equilibrium constant $\mathrm{K} _{\mathrm{c}}=2.1 \times 10^{-3}$. At equilibrium mole $%$ of $\mathrm{NO}$ was 1.8. Estimate the initial composition of air in mole fractions of $\mathrm{N} _{2}$ and $\mathrm{O} _{2}$.

4. $\quad 0.96 \mathrm{~g}$ of $\mathrm{HI}$ were heated to attain equilibrium $2 \mathrm{HI} \rightleftharpoons \mathrm{H} _{2}+\mathrm{I} _{2}$. The reaction mixture on titration requires $15.7 \mathrm{~mL}$ of $\mathrm{N} / 10$ hypo solution. Calculate degree of dissociation of $\mathrm{HI}$.

5. At $340 \mathrm{~K}$ and one atmospherec pressure, $\mathrm{N} _{2} \mathrm{O} _{4}$ is $66 %$ dissociated into $\mathrm{NO} _{2}$. What volume would $10 \mathrm{~g}$ of $\mathrm{N} _{2} \mathrm{O} _{4}$ occupy under these conditions?

6. One mole of $\mathrm{N} _{2}$ and three mole of $\mathrm{PCl} _{5}$ are placed in a 100 litre vessel heated to $227^{\circ} \mathrm{C}$. The equilibrium pressure is $2.05 \mathrm{~atm}$. Assuming ideal behaviour, calculate degree of dissociation of $\mathrm{PCl} _{5}$ and $\mathrm{K} _{\mathrm{p}}$ of the reaction.

7. A vessel at $1000 \mathrm{~K}$ contains $\mathrm{CO} _{2}$ with pressure of $0.5 \mathrm{~atm}$. Some of the $\mathrm{CO} _{2}$ is converted into $\mathrm{CO}$ on addition of graphite. Calculate the value of $\mathrm{K}$, if total pressure at equilibrium is $0.8 \mathrm{~atm}$.

8. A two litre vessel contains 0.48 mole of $\mathrm{CO} _{2}, 0.48$ mole of $\mathrm{H} _{2}, 0.96$ mole of $\mathrm{H} _{2} \mathrm{O}$ and 0.96 mole of $\mathrm{CO}$ at equilibrium,

$\quad$ a.$\quad$ How many mole and how many ’ $g$ ’ of $\mathrm{H} _{2}$ must be added to bring the concentration of $\mathrm{CO}$ to $0.6 \mathrm{M}$ ?

$\quad$ b.$\quad$ How many mole and how many ’ $\mathrm{g}$ ’ of $\mathrm{CO} _{2}$ must be added to bring the concentration of CO to $0.6 \mathrm{M}$ ?

$\quad$ c.$\quad$ How many mole of $\mathrm{H} _{2} \mathrm{O}$ must be removed lo bring the concentration $\mathrm{CO}$ to $0.6 \mathrm{M}$ ?

9. The standard Gibbs function at $400 \mathrm{~K}$ for the isomerization of cis 2-pentene to trans 2-pentene is $-3.67 \mathrm{KJ} \mathrm{mol}^{-1}$. Calculate $\mathrm{K} _{\mathrm{p}}$.

10. The dissociation pressure of solid ammonium hydro-sulphide at $27^{\circ} \mathrm{C}$ is $60 \mathrm{~cm}$. What will be the total pressure when it dissociates at the same temperature in presence of $\mathrm{NH} _{3}$ at a pressure of 45 $\mathrm{cm}$ ? Assume $\mathrm{NH} _{4} \mathrm{HS}$ dissociates completely into $\mathrm{NH} _{3}$ and $\mathrm{H} _{2} \mathrm{~S}$.