Thermodynamics: Means flow of heat

One of the fundamental subject in physical chemistry

It’sa science of macroscopic properties i.e. properties of matter in bulk

It deals with energy changes accompanying all types of physical and chemical processes

It predicts the feasibility or spontaneity of a process, including a chemical reaction, under a given set of conditions

It helps to determine the extent to which a process can proceed before attainment of equilibrium

Terms used in Thermodynamics

System : Part of universe chosen for thermodynamic studies.

Surroundings: Remaining universe other than the system.

Universe $=$ system + surroundings

Boundary: Real or imaginary surface that separates the system from its surroundings

Classification of Systems

On the basis of possibility of movement of matter and energy in or out of the system.

(a) Open System: It can exchange both matter and energy with its surroundings.

e.g. tea kept in on open vessel.

(b) Closed System : It can exchange only energy with its surroundings but not matter.

e.g. tea kept in closed vessel.

(c) Isolated System : It can neither exchange matter nor energy with its surroundings.

e.g. tea kept in thermos flask.

State of the System

A system is said to be in a definite state if each of its measurable property has a definite value.

A system is described by specifying some or all of its $p, V, T$ and composition.

State of the system is specified by state functions or state variables.

Types of Function / Variables

(a) State Function

A physical quantity whose value depends upon the state of the system and does not depend upon the path by which the state has been attained.

e.g. p, $V, T$, internal energy, enthalpy, entropy

(b) Path Function

A physical quantity which depends on the path by which change is brought.

e.g. work and heat.

Macroscopic Properties of the System

(a) Intensive Properties

Properties which do not depend upon the amount of the substance. e.g. pressure, density, temperature, surface tension, boiling point, refractive index etc.

(b) Extensive Properties

Properties which depend upon the amount of the substance.

e.g. volume, mass, heat capacity, number of moles etc.

$\frac{\text { Extensive property }}{\text { Extensive property }}=$ Intensive property e.g. $\frac{\text { Mass }}{\text { Volume }}=$ Density

(c) Molar Property $\left(\boldsymbol{x} _{\mathrm{m}}\right)$

Value of an extensive property ’ $x$ ’ of the system for 1 mole of the substance.

$ x _{m}=\frac{x}{n}$ (Independent of the amount of matter $(\mathrm{n})$ )

All the molar properties are intensive properties.

Types of Processes

(a) Reversible Process

A process which is carried out infinitesimally slowly by a series of steps such that system and surroundings are always in near equilibrium with each other.

At any moment, the process can be reversed by an infinitesimal change.

(b) Irreversible Process

A process which cannot be reversed by small change.

Irreversible processes are carried out at finite rates.

(c) Adiabatic Process

A process during which no heat can flow in or out of the system. $\mathrm{d} q=0$

(d) Isothermal Process

It is carried out at constant temperature

$\mathrm{d} T=0$

(e) Isobaric Process

It is carried out at constant pressure

$\mathrm{d} p=0$

(f) Isochoric Process

During the process, volume of the system remains constant

$\mathrm{d} V=0$

$p-V$ graph for various thermodynamic processes

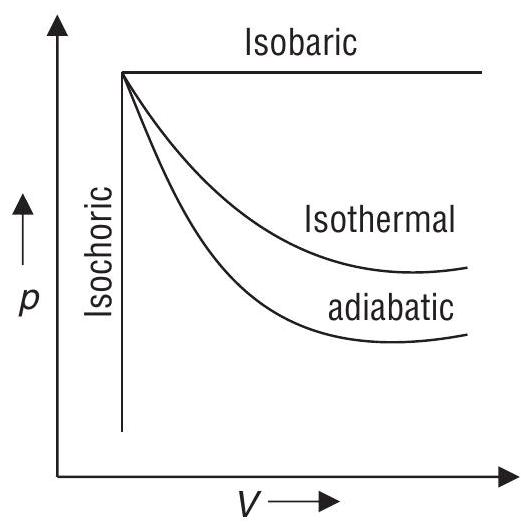
(g) Cyclic Process

When a system undergoes a series of changes and finally returns to its initial state.

Common modes of transfer of energy between system and surroundings

$\quad$ Heat $(q)$

$\quad$ Work $(w)$

Internal Energy (U)

It is the sum of all types of energies, a system may have like chemical, electrical, mechanical or any other type of energy.

It is a state function and an extensive property

Absolute measurement of $U$ is not possible so change in internal energy, $\Delta U$ is considered.

$$ \Delta U=U _{1}-U _{i} $$

where, $U _{\mathrm{f}}$ and $U _{\mathrm{i}}$ are the internal energies of final and initial states, respectively.

U of the system may change, when

Heat passes into or out of the system

Work is done on or by the system

Matter enters or leaves the system

At constant volume

$\qquad\Delta U=q$

$ q _{v}=$ heat absorbed or evolved at const. volume

Sign Convention

If energy is released, $\Delta U=-\mathrm{ve}$

If energy is absorbed, $\Delta U=+v e$

Work(w)

A form of energy transferred from system to the surroundings or from surroundings to the system due to difference in some property (other than temperature) between system and surroundings

Types of work

Mechanical work (due to difference in pressure)

work of expansion or compression or $p$ $-V$ work

Mechanical work $=$ force $x$ displacement

Electrical work (due to difference in electrical potential) $=-E m f x$ quantity of electricity passed

Sign Convention

If work is done on the system, $w=+\mathrm{ve}$ (compression)

If work is done by the system, $w=-\mathrm{ve}$ (expansion)

Heat

It is a form of energy exchanged between system and surroundings due to difference in temperature between system and surroundings

Sign Convention

If heat is absorbed (endothermic reaction), $q=+\mathrm{ve}$

If heat is released (exothermic reaction), $q=-\mathrm{ve}$

Units of work, heat and energy

SI unit of work $=\mathrm{J}$ or Nm$^{-1}$

Cgs unit of work $=$ erg or dyne $\mathrm{cm}^{-1}$

$1 \mathrm{~J}=10^{7} \mathrm{ergs}=0.239 \mathrm{cal}$

$1 \mathrm{~kJ}=1000 \mathrm{~J}$

$1 \mathrm{Latm}=101.3 \mathrm{~J}$

$1 \mathrm{cal}=4.184 \mathrm{~J}=4.184 \times 10^{7} \mathrm{erg}=41.293 \mathrm{~atm} \mathrm{~cm}^{3}$

$1 \mathrm{eV}=1.602 \times 10^{-19} \mathrm{~J} \mathrm{molecule}^{-1}=96.48 \mathrm{~kJ} \mathrm{~mol}^{-1}$

$=23.06 \mathrm{kcal} \mathrm{mol}^{-1}$

$=8065.5 \mathrm{~cm}^{-1}$

$\quad 1$ cal $>1 \mathrm{~J}>1$ erg $>1$ ev

Work done (w) in various processes

Work of expansion / compression or $p-V$ work

a) Work done in irreversible isothermal expansion against a constant external pressure $\left(p _{\text {ext }}\right)$

$$ w=-p _{\text {ext }} \Delta V=-p _{\text {ext }}\left(V _{2}-V _{1}\right) $$

$V _{2}$ and $V _{1}$ represent the final and initial volumes, respectively

b) Wore done in isothermal reversible expansion of $n$ moles of an ideal gas

$$ w=-2.303 n R T \log \frac{V _{2}}{V _{1}}=-2.303 n R T \log \frac{p _{1}}{p _{2}} $$

(-ve sign has been used as it is work of expansion i.e. work done by the system)

c) Free Expansion (Expansion in vaccum)

Ideal gas: $\quad p _{\text {ext }}=0, w=0, \Delta U=0, q=0$

Real gas: $\quad p _{\text {ext }}=0, w=0$

Work and heat are not state functions, they are path functions

First Law of Thermodynamics

The energy of an isolated system is constant. Mathematically

$$ \Delta U=q+w $$

This law is also known as law of conservation of energy i.e. energy can neither be created nor destroyed

$\quad$ For an ideal gas undergoing isothermal changes $(\Delta T=0), \Delta U=0$

Isothermal and Free Expansion of an Ideal Gas

$p _{\text {ext }}=0$

$w=0$

Also, $q=0$ and $\Delta U=0$

1. For isothermal irreversible change

$q=-W=p _{\mathrm{ext}}\left(V _{2}-V _{1}\right)$

2. For isothermal reversible change

$q=-w=n R T \ln \frac{V _{2}}{V _{1}}=2.303 n R T \log \frac{V _{2}}{V _{1}}$

3. For adiabatic change, $q=0$

$\Delta U=W _{\mathrm{ad}}$

Comparison of reversible, irreversible and adiabatic work

$W _{\text {rev }}>W _{\text {ireve }}>W _{\text {ad }}$

For reversible expansion, $p _{\text {ext }}$ has maximum value (only infinitesimally smaller than $p _{\text {int }}$ ), work done in reversible expansion is the maximum work for a given change in volume.

Enthalpy $(\boldsymbol{H})$

It is the heat evolved or absorbed at constant pressure.

It is a state function and an extensive property.

For exothermic reactions, $\Delta H=$-ve; heat is evolved during the reaction

For endothermic reactions, $\Delta H=+v e$; heat is absorbed from the surroundings

$ H=U+p V$

$ \Delta H=\Delta U+p \Delta V$ (at const. pressure)

$ \Delta H=q _{p}$ (heat absorbed at constant pressure)

$ \Delta U=q _{v}$ (heat absorbed at constant volume)

Also,

$\Delta H=\Delta U+\Delta n _{g} R T$

where, $\Delta n _{9}=$ difference between the number of moles of the gaseous products and those of the gaseous reactants.

The difference in $\Delta U$ and $\Delta H$ is insignificant for solids and liquids.

Heat capacity (C)

Amount of heat required to raise the temperature of the system by $1^{\circ} \mathrm{C}$ or $1 \mathrm{~K}$

$$ \begin{aligned} & C=\frac{q}{\Delta T} \\ & C _{\mathrm{m}} \propto \text { Amount of Substance } \end{aligned} $$

It is an extensive property

Units : $\mathrm{JK}^{-1}$

Specific Heat Capacity (c)

Amount of heat required to raise the temperature of one gram (unit mass) of a substance by $1^{\circ} \mathrm{C}$ or $1 \mathrm{~K}$

It is an intensive property

Units : $\mathrm{Jg}^{-1} \mathrm{~K}^{-1}$

$$ q=c \times m \times \Delta T=C \Delta T $$

where, $q=$ heat required to raise the temperature of a sample

$c=$ specific heat capacity of the substance

$m=$ mass of the sample; $\Delta T$ = temperature change

Specific heat capacity of water is $1 \mathrm{cal} \mathrm{g}^{-1} \mathrm{~K}^{-1}$ or $4.184 \mathrm{~J} \mathrm{~g}^{-1} \mathrm{~K}^{-1}$

Molar heat capacity ( $\left.\boldsymbol{C} _{\mathrm{m}}\right)$

Amount of heat required to raise the temperature of 1 mole of the substance by $1^{\circ} \mathrm{C}$ or $1 \mathrm{~K}$

$$ C _{\mathrm{m}}=\frac{C}{n} $$

where, $C$ is the heat capacity of ’ $n$ ’ moles of the substance.

Unit: J mol ${ }^{-1} \mathrm{~K}^{-1}$

It is an intensive property

Types of Heat Capacities

$ C _{\mathrm{v}}$ - heat capacity at constant volume

$ C _{\mathrm{P}}$-heat capacity at constant pressure

For an ideal gas

$$ \begin{aligned} C _{\mathrm{V}}= & \frac{\mathrm{d} U}{\mathrm{~d} T} \text { and } C _{\mathrm{p}}=\frac{\mathrm{d} H}{\mathrm{~d} T} \\ & C _{\mathrm{p}}-C _{\mathrm{V}}=R \quad \text { (for } 1 \text { mole of an ideal gas) } \end{aligned} $$

For $n$ moles

$\begin{gathered}C_{\mathrm{p}}-C_{\mathrm{V}}=n R \\ \gamma=\frac{C_{\mathrm{p}}}{C_{\mathrm{V}}}\end{gathered}$(ratio of $C _{\mathrm{p}} / C _{\mathrm{v}}$ represented by $ \gamma$ )

Importance of $C _{\mathrm{p}}$ and $C _{\mathrm{v}}$

Ratio of $C _{\mathrm{p}}$ and $C _{\mathrm{v}}$, represented by $\gamma$, is related to atomicity of the gas

$ \begin{array}{|c|c|c|c|} \hline & C_{p} & C_{v} & \gamma \\ \hline \text{Monoatomic Gas} & 5 \mathrm{cal} & 3 \mathrm{cal} & 1.67 \\ \hline \text{Diatomic Gas} & 7 \mathrm{cal} & 5 \mathrm{cal} & 1.40 \\ \hline \text{Triatomic Gas} & 8 \mathrm{cal} & 6 \mathrm{cal} & 1.33 \\ \hline \end{array} $

Measurement of $\Delta \boldsymbol{U}$ and $\Delta \boldsymbol{H}$

Since, $\Delta U=q _{\mathrm{N}}$

So, $\Delta U$ is determined by measuring the heat lost or gained $\left(q _{v}\right)$ for the reaction or process in a closed vessel (constant volume) e.g. Bomb calorimeter.

$\Delta H=q _{\mathrm{p}}$

In this case, the heat lost or gained $\left(q _{p}\right)$ is determined when the reaction is carried out in an open vessel.

If reaction involves only solids & liquids or $\Delta \mathrm{n} _{g}=0$, then $\Delta \mathrm{H}=\Delta \mathrm{U}$

For a cyclic process : $\Delta U=0, \Delta H=0$

During isothermal expansion of an ideal gas, $\Delta U=0, \Delta T=0$ and $\Delta H=0$. Thus, it is an isoenthalpic process.

Enthalpy change of the reaction $\left(\Delta _{\mathrm{r}} \boldsymbol{H}\right)$

The amount of heat absorbed or evolved in a chemical reaction when moles of reactants and products being the same as indicated by the balanced chemical reaction.

Standard Conditions

Pressure $=1$ bar

Temperature $=$ any specified temperature

The standard state of a substance at a specified temperature is its pure form at 1 bar.

Standard conditions are denoted by adding the superscript 0 or $\Theta$ to the symbol. e.g. $\Delta H^{P} /$ $\Delta H^{\ominus}$

Standard enthalpy of a reaction $\Delta _{\mathrm{r}} \boldsymbol{H}^{\ominus}$

The enthalpy change accompanying the reaction when all the reactants and products are taken in their standard states ( 1 bar pressure and at any specified temperature, generally $298 \mathrm{~K}$ ).

Depending upon the nature of the reaction, enthalpy of the reaction is named accordingly.

Enthalpy of combustion, $\Delta _{\mathrm{c}} \boldsymbol{H}$

The enthalpy change when one mole of a substance is burnt completely in excess of oxygen.

Enthalpy of formation $\Delta _{\mathrm{r}} H$

The enthalpy change when one mole of a substance is formed from its elements under given conditions of temperature and pressure.

Enthalpy of neutralization $\Delta _{\text {neut }} \boldsymbol{H}$

The enthalpy change when one gram equivalent of the acid is neutralized by a strong base.

Enthalpy of solution $\Delta _{\text {sol }} \boldsymbol{H}$

The enthalpy change when one mole of the substance is dissolved in a specified amount of the solvent.

$$ \Delta _{\text {sol }} H^{\circ}=\Delta _{\text {lattice }} H^{p}+\Delta _{\text {hyd }} H^{\circ} $$

For most of the ionic compounds

$ \Delta _{\text {sol }} \mathrm{H}^{\circ}=+\mathrm{ve}$

Enthalpy of Hydration $\Delta _{\text {hyd }} \boldsymbol{H}$

Amount of heat evolved or absorbed when one mole of an anhydrous salt combines with the required number of water molecules to form the hydrated salt.

Dissociation process of the compounds is endothermic

Solubility of most salts in $\mathrm{H} _{2} \mathrm{O}$ increases with rise of $T$

Enthalpy of atomization $\Delta _{\mathrm{a}} \boldsymbol{H}$ :

The enthalpy change when one mole of a substance dissociates into gaseous atoms.

Enthalpy of Reaction

$\Delta _{\mathrm{r}} \mathrm{H}^{0}=\Sigma \Delta _{\mathrm{i}} \mathrm{H}^{0}$ (products) $-\Sigma \Delta _{\mathrm{i}} \mathrm{H}^{0}$ (reactants)

$\Delta _{\mathrm{f}} \mathrm{H}^{0}$ is the standard enthalpy of formation. For elements in their most stable states $\Delta _{\mathrm{i}} \mathrm{H}^{0}$ is taken as zero.

For example, the most stable states of oxygen, bromine, iodine are $\mathrm{O} _{2}(\mathrm{~g}), \mathrm{Br} _{2}(\mathrm{l}), \mathrm{I} _{2}(\mathrm{~s})$

whereas for carbon $\mathrm{C}$ (graphite), for sulphur $\mathrm{S} _{8}$ (rhombic)

$\Delta _{\mathrm{t}} \mathrm{H}^{0}$ for all these substances is equal to zero.

Depending upon the type of process involving a phase change, the enthalpy change (for one mole of a substance) is named accordingly.

Enthalpy of fusion, $\Delta _{\text {tus }} \boldsymbol{H}$

Enthalpy change that accompanies melting of one mole of a solid substance at constant temperature and pressure.

Melting of a solid is endothermic process

$\Rightarrow \Delta _{\text {fus }} H=+$ ve (all)

Enthalpy of vaporization $\Delta _{\text {vap }} H$

Amount of heat required to vaporize one mole of a liquid at constant temperature and pressure.

Enthalpy of sublimation $\Delta _{\text {sub }} \boldsymbol{H}$

Enthalpy change when one mole of a solid substance sublimes at a constant temperature and pressure.

$$ \Delta _{\text {sub }} H=\Delta _{\text {fus }} H+\Delta _{\text {vap }} H $$

Note: Magnitude of enthalpy change depends on the strength of the intermolecular interactions in the substance undergoing the phase transformations.

Hess’s Law of constant heat summation

the total enthalpy change accompanying a chemical reaction is the same whether the reaction takes place in one or more steps.

$\Delta H=\Delta H _{1}+\Delta H _{2}+\Delta H _{3}$

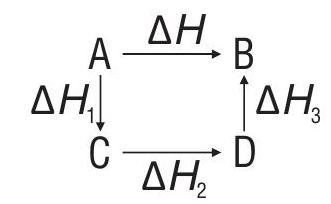
When chemical equations are added, subtracted or multiplied, the enthalpy changes can also be added, subtracted or multiplied.

The sign of $\Delta _{\mathrm{r}} \mathrm{H}$ gets reversed on reversing a chemical equation.

Bond enthalpy $\left(\Delta _{\text {bond }} \mathbf{H}^{\circ}\right)$

The amount of energy required to dissociate one mole of bonds present between the atoms in the gaseous molecules. Two separate terms are used in thermodynamics (i) bond dissociation enthalpy (ii) mean bond enthalpy.

Bond dissociation enthalpy is the change in enthalpy when one mole of covalent bonds of a gaseous compound is broken to form products in gas phase.

Mean bond enthalpy is the average value of bond dissociation enthalpy of a particular type of bond present in different compounds.

$\Delta _{r} H=\Sigma B . E _{\text {reactant }}-\Sigma B . E _{\text {product }}$

Units: $\mathrm{kJ} / \mathrm{mol}$

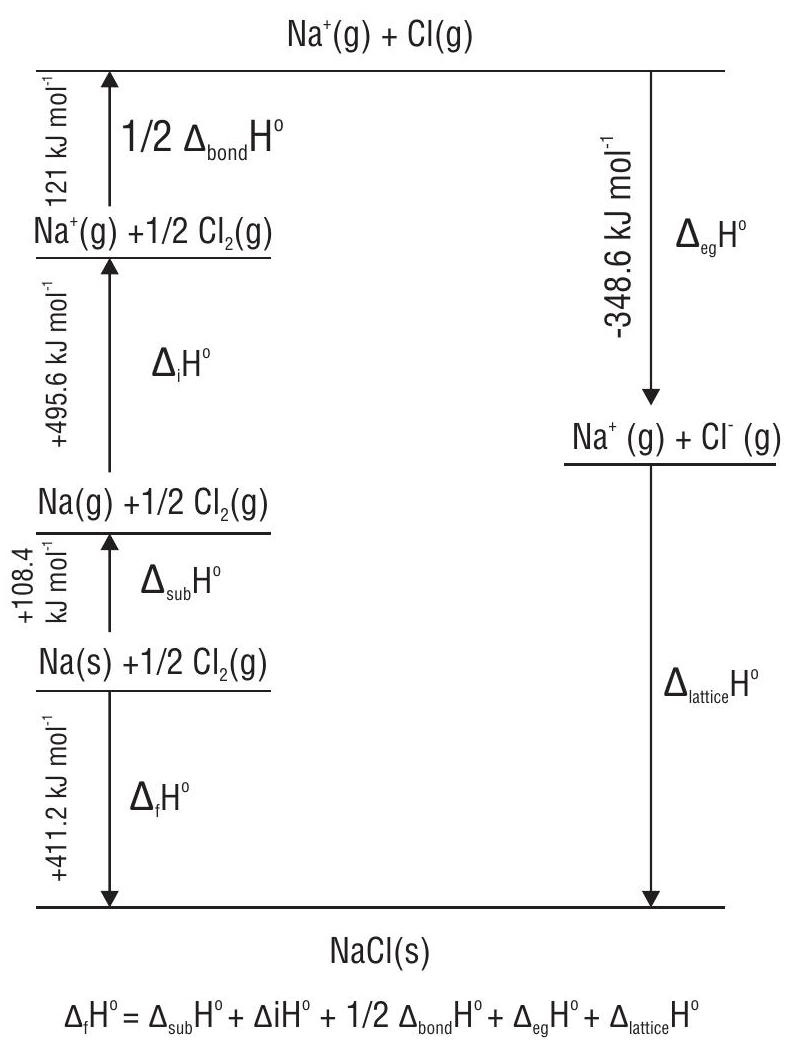
Calculation of lattice enthalpy using Born-Haber cycle

Lattice enthalpy $\left(\Delta _{\text {altite }} \mathrm{H}^{0}\right)$ : is the enthalpy change which occurs when one mole of an ionic compound in crystalline state dissociates into its ions in gaseous state.

The sum of the enthalpy changes round a Born-Haber cycle is zero.

Enthalpy diagram for lattice enthalpy of NaCl (Born Haber cycle for NaCl).

Spontaneous process : a physical or chemical change that occurs on its own. It may or may not need initiation.

Non-spontaneous process : a process which cannot take place by itself nor by initiation.

Two factors which govern the spontaneity of a process:

1. Tendency to attain minimum energy state.

2. Tendency to attain maximum randomness or disorder.

First law of thermodynamics puts no restriction on the direction of heat flow or direction of any process.

The flow of heat is unidirectional from higher temperature to lower temperature.

Most of the processes occur spontaneously only in one direction under a given set of conditions of temperature and pressure.

Decrease in enthalpy is not the only criterion for spontaneity.

Entropy, $\mathbf{S}$ : is a measure of randomness or disorder of the system.

It is a state function i.e. path independent

Qualitatively, $\Delta S$ in a chemical reaction is estimated by a consideration of the structures of the species.

A crystalline solid will have the lowest entropy, whereas the gaseous state will have the highest entropy.

The order of randomness and thus, the entropy is:

Gas > liquid > solid

For a reversible change at constant temperature

$\Delta S=\frac{q _{\mathrm{rev}}}{T}$

$q _{\text {rev }}=$ heat absorbed or evolved at absolute temperature $T$

Unit: $\mathrm{JK}^{-1} \mathrm{~mol}^{-1}$

In achemical reaction:

$\Delta _{\mathrm{r}} S=\Sigma S _{\text {products }}-\Sigma S _{\text {reactants }}$

Entropy changes during phase transformations

(a) $\Delta _{\text {tus }} S=\frac{\Delta _{\text {tus }} H}{T _{\mathrm{m}}}$

$\quad \Delta _{\text {tus }} H=$ enthalpy of fusion per mole

$\quad T _{\mathrm{m}}=$ melting temperature in Kelvin

(b) $\Delta _{\text {vap }} S=\frac{\Delta _{\text {vap }} H}{T _{\mathrm{b}}}$

$\quad \Delta _{\text {fus }} \mathrm{H}=$ enthalpy of vapourization per mole

$\quad \mathrm{T} _{\mathrm{b}}=$ boiling temperature in kelvin

(c) $\Delta _{\text {sub }} S=\frac{\Delta _{\text {sub }} H}{T}$

$\quad \Delta _{\text {sub }} H=$ enthalpy of sublimation at the temperature $T$.

For all spontaneous processes, the total entropy change must be positive

$ \Delta S _{\text {total }}=\Delta S _{\text {system }}+\Delta S _{\text {surr }}>0$

$ \Delta S _{\text {total }}=+v e \Rightarrow$ Process is spontaneous

$\mathrm{S} _{\text {total }}=-\mathrm{ve} \Rightarrow$ Direct process is non-spontaneous; the reverse process is spontaneous.

When a system is in equilibrium, the entropy is maximum and the change in entropy, $\Delta S=$ 0 .

$\Delta U$ does not discriminate between reversible and irreversible process whereas $\Delta S$ does.

$ \Delta U=0$ (for both reversible & irreversible expansion for an ideal gas; under isothermal conditions)

$ \Delta S _{\text {total }}>0$ (for irreversible process) and $\Delta S _{\text {total }}=0$ (for reversible process)

Second Law of Thermodynamics

For a spontaneous process in an isolated system, the change in entropy is positive. Or

It is impossible to convert heat completely into work without leaving some effects elsewhere.

Gibbs Energy, $G$

The maximum amount of energy available to a system, during a process, that can be converted into useful work.

It is a state function and an extensive property

Units: $\mathrm{Jmol}^{-1}$

Gibbs Helmholtz Equation

$$ \begin{aligned} & \Delta G=\Delta H-T \Delta S \quad(\text { at constant } T \text { and } p) \\ & \Delta G=-T \Delta S _{\text {total }} \end{aligned} $$

$\Delta \mathrm{G}$ gives a criteria for spontaneity at constant pressure and temperature

If, $\Delta \mathrm{G}=-\mathrm{ve}(<0) \Rightarrow$ Process is spontaneous.

If, $\Delta \mathrm{G}=+\mathrm{ve}(>0) \Rightarrow$ Process is non-spontaneous

It, $\Delta \mathrm{G}=0 \Rightarrow$ Process is in equilibrium

$\Delta \mathrm{G}^{0}$ is the Gibbs energy change for a process when all the reactants and products are in their standard states.

Relationship between equilibrium constant $(K)$ and $\Delta G^{\circ}$

$$ \Delta G^{0}=-2.303 R T \log K $$

Relationship between electrical work done in the galvanic cell and $\triangle G$

$\qquad \Delta G=-n F E _{\text {col }}$

$\qquad E _{\text {enl }}=$ emf of the cell

$\qquad n=n 0$. of moles of electrons involved

$\qquad F=$ Faraday’s constanti.e. $96500 \mathrm{C} \mathrm{mol}^{-1}$

If reactants and products are in their standard states

$\qquad \Delta G^{\circ}=-n F E _{\text {cell }}^{0}$

$\qquad E^{0}=$ standard emf of the cell

Effects of signs of $\Delta H, \Delta S$ and $T$ on the spontaneity of a process

Solved Examples

Question 1. How many calories are required to heat $40 \mathrm{gram}$ of argon from $40^{\circ}$ to $100^{\circ} \mathrm{C}$ at constant volume? ( $\mathrm{R}=2 \mathrm{cal} \mathrm{K}^{-1} \mathrm{~mol}^{-1}$ )

(a) 120

(b) 2400

(c) 1200

(d) 180

Question 2. $4.48 \mathrm{~L}$ of an ideal gas at NTP requires 12.0 calories to raise its temperature by $15^{\circ} \mathrm{C}$ at constant volume. The $\mathrm{C} _{\mathrm{p}}$ of the gas is

(a) $3 \mathrm{cal}$

(b) $4 \mathrm{cal}$

(c) $7 \mathrm{cal}$

(d) $6 \mathrm{cal}$

Question 3. The standard enthalpy of formation of $\mathrm{NH} _{3}$ is $-46.0 \mathrm{~kJ} \mathrm{~mol}^{-1}$. If the enthalpy of formation of $\mathrm{H} _{2}$ from its atoms is $-436 \mathrm{~kJ} \mathrm{~mol}^{-1}$ and that of $\mathrm{N} _{2}$ is $-712 \mathrm{~kJ} \mathrm{~mol}^{-1}$, the average bond enthalpy of $\mathrm{N}-\mathrm{H}$ bond in $\mathrm{NH} _{3}$ is

(a) $-1102 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(b) $-964 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(c) $+352 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(d) $1056 \mathrm{~kJ} \mathrm{~mol}^{-1}$

Question 4. The standard molar enthalpies of formation of cyclohexane (I) and benzene (I) at $25^{\circ} \mathrm{C}$ are - 156 and $+49 \mathrm{~kJ} \mathrm{~mol}^{-1}$, respectively. The standard enthalpy of hydrogenation of cyclohexene (I) at $25^{\circ} \mathrm{C}$ is $-119 \mathrm{~kJ} \mathrm{~mol}^{-1}$. The magnitude of the resonance energy is :

(a) $-357 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(b) $-152 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(c) $-205 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(d) $+152 \mathrm{~kJ} \mathrm{~mol}^{-1}$

Show Answer

Solution: $b$

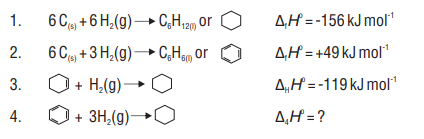
Enthalpy change for the hydrogenation of benzene should be three times the enthalpy of hydrogenation of cyclohexene

$\Delta _{4} H^{\rho}=3 \times \Delta _{\text {H }} H^{\rho}$

$=3(-119)=-357 \mathrm{~kJ} \mathrm{~mol}-1$

On adding equations (2) and (4), we get

(5) $6 \mathrm{C}(\mathrm{s})+6 \mathrm{H} _{2}(\mathrm{~g}) \rightarrow \square$ $\Delta _{6} \mathrm{H}^{0}=-308 \mathrm{~kJ} \mathrm{~mol}^{-1}$

This reaction also gives the energy of formation of cyclohexane.

The difference in the enthalpy of formation calculated by these alternate paths is due to resonance stabilization of benzene.

Resonance energy of benzene $=-308-(-156)$

$=-152 \mathrm{~kJ} \mathrm{~mol}^{-1}$

Question 5. The enthalpy of formation of $\mathrm{CO} _{2}(\mathrm{~g}), \mathrm{H} _{2} \mathrm{O}(\mathrm{I})$ and propene $(\mathrm{g})$ are $-393.5,-285.8$ and $20.42 \mathrm{~kJ}$ $\mathrm{mol}^{-1}$, respectively. The enthalpy of isomerization of cyclopropane to propene is $-33.0 \mathrm{~kJ} \mathrm{~mol}^{-1}$. The enthalpy change for combustion of cyclopropane is :

(a) $-2058.32 \mathrm{~kJ}$

(b) $-2091.32 \mathrm{~kJ}$

(c) $+2058.32 \mathrm{~kJ}$

(d) $+2091.32 \mathrm{~kJ}$

Practice Questions

Question 1. For which of the process, $\Delta S$ is negative?

(a) $\mathrm{H} _{2}(\mathrm{~s}) \rightarrow 2 \mathrm{H}(\mathrm{g})$

(b) $ \mathrm{N} _{2}(\mathrm{~g}, 1 \mathrm{~atm}) \longrightarrow \mathrm{N} _{2}(\mathrm{~g}, 8 \mathrm{~atm})$

(c) $2 \mathrm{SO} _{3}(\mathrm{~g}) \rightarrow 2 \mathrm{SO} _{2}(\mathrm{~g})+\mathrm{O} _{2}(\mathrm{~g})$

(d) $\mathrm{C} _{\text {(diamond) }} \rightarrow \mathrm{C} _{\text {(graphite) }}$

Question 2. The favourable conditions for a spontaneous reaction are

(a) $T \Delta S>\Delta H, \Delta H=+\mathrm{ve}, \Delta S=+\mathrm{ve}$

(b) $T \Delta S>\Delta H, \Delta H=+$ ve, $\Delta S=-$ ve

(c) $T \Delta S=\Delta H, \Delta H=-\mathrm{ve}, \Delta S=-\mathrm{ve}$

(d) $T \Delta S=\Delta H, \Delta H=+v e, \Delta S=+v e$

Question 3. Certain reaction is at equilibrium at $82^{\circ} \mathrm{C}$ and the enthalpy change for this reaction is $21.3 \mathrm{~kJ}$. The value of $\Delta S\left(\right.$ in JK $\left.{ }^{-1} \mathrm{~mol}^{-1}\right)$ for the reaction is

(a) 55.0

(b) 60.0

(c) 68.5

(d) 120.0

Question 4. Which of the following thermodynamic relation is correct?

(a) $\mathrm{d} G=V \mathrm{~d} P-S \mathrm{~d} T$

(b) $ \mathrm{d} U=P \mathrm{~d} V+T \mathrm{~d} S$

(c) $\mathrm{d} H=V \mathrm{~d} P+T \mathrm{~d} S$

(d) $\mathrm{d} G=V \mathrm{~d} P+S \mathrm{~d} T$

Question 5. For a gaseous reaction $\mathrm{A}+3 \mathrm{~B} \rightleftharpoons 2 \mathrm{C}, \Delta H^{\circ}=-90.0 \mathrm{~kJ}, \Delta S^{\circ}=-200.0 \mathrm{JK}^{-1}$ at $400 \mathrm{~K}$. What is $\Delta G^{\circ}$ for the reaction $\frac{1}{2} A+\frac{3}{2} B \rightleftharpoons \mathrm{C}$ at $400 \mathrm{~K}$ ?

(a) $-5.0 \mathrm{~kJ}$

(b) $-10.0 \mathrm{~kJ}$

(c) $-15.0 \mathrm{~kJ}$

(d) $-20.0 \mathrm{~kJ}$

Question 6. The values of $\Delta H$ and $\Delta S$ for the reaction $\mathrm{C} _{\text {(graphite })}+\mathrm{CO} _{2}(\mathrm{~g}) \rightarrow 2 \mathrm{CO}(\mathrm{g})$ are $170 \mathrm{~kJ}$ and $170 \mathrm{JK}^{-1}$ respectively. This reaction will be spontaneous at

(a) $910 \mathrm{~K}$

(b) $1110 \mathrm{~K}$

(c) $510 \mathrm{~K}$

(d) $710 \mathrm{~K}$

Question 7. A reaction is spontaneous at low temperature but non-spontaneous at high temperature. Which of the following is true for the reaction?

(a) $\Delta H>0, \Delta S>0$

(b) $\Delta H<0, \Delta S>0$

(c) $\Delta H>0, \Delta S<0$

(d) $\Delta H<0, \Delta S<0$

Question 8. $\Delta \mathrm{G}^{\circ}$ for a reaction is $46.06 \mathrm{kcal} / \mathrm{mole}, K _{\mathrm{p}}$ for the reaction at $300 \mathrm{~K}$ is

(a) $10^{-8}$

(b) $10^{-22.22}$

(c) $10^{-33.53}$

(d) none of these

Question 9. The enthalpy change for the reaction, $\mathrm{Zn}(\mathrm{s})+2 \mathrm{H}^{+}(\mathrm{aq}) \longrightarrow \mathrm{Zn}^{2+}(\mathrm{aq})+\mathrm{H} _{2}(\mathrm{~g})$ is $-154.4 \mathrm{~kJ} \mathrm{~mol}^{-1}$. The formation of $2 \mathrm{~g}$ of hydrogen expands the system by $22.4 \mathrm{~L}$ at $1 \mathrm{~atm}$ pressure. The internal energy change of the reaction will be

(a) $156 . \mathrm{kJ}$

(b) $-152.1 \mathrm{~kJ}$

(c) $-154.4 \mathrm{~kJ}$

(d) None of these is correct

Question 10. Two moles of an ideal gas is expanded isothermally and reversibly from 1 litre to 10 litre at $300 \mathrm{~K}$. The enthalpy change (in $\mathrm{kJ}$ ) for the process is

(a) $ 11.4 \mathrm{~kJ}$

(b) $-11.4 \mathrm{~kJ}$

(c) $0 \mathrm{~kJ}$

(d) $ 4.8 \mathrm{~kJ}$

Question 11. When 0.1 mole of a gas absorbs $41.75 \mathrm{~J}$ of heat at constant volume, the rise in temperature occurs equal to $20^{\circ} \mathrm{C}$. The gas must be

(a) triatomic

(b) diatomic

(c) polyatomic

(d) monoatomic

Question 12. An insulated container is divided into two compartments. One compartment contains an ideal gas at a pressure $P$ and temperature $T$ while in the other compartment there is perfect vacuum. If a hole is made in the partition wall, which of the following will be true?

(a) $\Delta U=0$

(b) $\quad w=0$

(c) $\Delta T=0$

(d) All the three are true

Question 13. One mole of a non-ideal gas undergoes a change of state $(2.0 \mathrm{~atm}, 3.0 \mathrm{~L}, 95 \mathrm{~K}) \longrightarrow(4.0 \mathrm{~atm}, 5.0$ $\mathrm{L}, 245 \mathrm{~K}$ ) with a change in internal energy, $\Delta \mathrm{U}=30.0 \mathrm{~L}$ atm. The change in enthalpy $(\Delta H)$ of the process in $\mathrm{L}$ atm is

(a) 44.0

(b) $ 42.3$

(c) 44.0

(d) not defined, because pressure is not constant

Question 14. An ideal gas is allowed to expand both reversibly and irreversibly in an isolated system. If $T _{i}$ is the initial temperature and $T _{t}$ is the final temperature, which of the following statements is correct?

(a) $\left(T _{t}\right) _{\text {reve }}>\left(T _{t}\right) _{\text {irev }}$

(b) $T _{\mathrm{t}}=T _{\mathrm{i}}$ for both reversible and irreversible processes

(c) $\left(T _{t}\right) _{\text {ireve }}>\left(T _{t}\right) _{\text {rev }}$

(d) $ T _{t}>T _{i}$ for reversible process but $T _{t}=T _{i}$ for irreversible processes

Question 15. One mole of an ideal gas expands freely and isothermally at $300 \mathrm{~K}$ from 10 litres to 100 litres. If $\Delta \underline{U}=0$, the value of $\Delta \mathrm{H}$ is

(a) $10 \mathrm{~kJ}$

(b) $200 \mathrm{~kJ}$

(c) zero

(d) $300 \mathrm{~kJ}$

Question 16. Which one of the following equations does not correctly represent the first law of thermodynamics for the given process?

(a) Isothermal process: $q=-w$

(b) Cyclic process: $q=-w$

(c) Isochoric process : $\Delta \underline{U}=\mathrm{q}$

(d) Adiabatic process : $\Delta \underline{U}=-\mathrm{w}$

Question 17. When $100 \mathrm{~g}$ of water is electrolysed at constant pressure of $1 \mathrm{~atm}$ and temperatureof $25^{\circ} \mathrm{C}$, the work of expansion is

(a) $-203.8 \mathrm{~kJ}$

(b) $-20.6 \mathrm{~kJ}$

(c) $-23.6 \mathrm{~kJ}$

(d) $-101.9 \mathrm{~kJ}$

Question 18. Work done in expansion of an ideal gas from $4 \mathrm{dm}^{3}$ to $6 \mathrm{dm}^{3}$ against a constant external pressure of $2.5 \mathrm{~atm}$ was used up to heat up $1 \mathrm{~mole}$ of water at $20^{\circ} \mathrm{C}$. The final temperature of water will be (Given: specific heat of water $=4.184 \mathrm{~J} \mathrm{~g}^{-1} \mathrm{~K}^{-1}$ )

(a) $\quad 23.7^{\circ} \mathrm{C}$

(b) $\quad 24.7^{\circ} \mathrm{C}$

(c) $\quad 25.7^{\circ} \mathrm{C}$

(d) $\quad 26.7^{\circ} \mathrm{C}$

Question 19. The bond dissociation energies of $X Y, X _{2}$ and $Y _{2}$ (all diatomic molecules) are in the ratio 1:1:0.5 and $\Delta _{1} \mathrm{H}$ for the formation of $\mathrm{XY}$ is $-200 \mathrm{KJ} \mathrm{mol}^{-1}$. The bond dissociation energy of $\mathrm{X} _{2}$ will be

(a) $400 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(b) $ 800 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(c) $200 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(d) $100 \mathrm{~kJ} \mathrm{~mol}^{-1}$

Question 20. Under which of the following condition is the relation $\Delta H=\Delta \underline{U}+p \Delta V$ valid for a closed system?

(a) constant pressure

(b) constant temperature

(c) constant temperature and pressure

(d) constant temperature, pressure and composition

Question 21. Given $\mathrm{NH} _{3}(\mathrm{~g})+3 \mathrm{Cl} _{2}(\mathrm{~g}) \rightleftharpoons \mathrm{NCl} _{3}(\mathrm{~g})+3 \mathrm{HCl}(\mathrm{g}) ;-\Delta H _{1}$

$\mathrm{N} _{2}(\mathrm{~g})+3 \mathrm{H} _{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH} _{3}(\mathrm{~g}) ;-\Delta \mathrm{H} _{2}$

$\mathrm{H} _{2}(\mathrm{~g})+\mathrm{Cl} _{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HCl}(\mathrm{g}) ; \Delta \mathrm{H} _{3}$

The heat of formation of $\mathrm{NCl} _{3}(\mathrm{~g})$ in the terms of $\Delta H _{1}, \Delta H _{2}$ and $\Delta H _{3}$ is

(a) $\Delta _{i} H=-\Delta H _{1}-\frac{\Delta H _{2}}{2}-\frac{3}{2} \Delta H _{3}$

(b) $\Delta _{i} H=\Delta H _{1}+\frac{\Delta H _{2}}{2}-\frac{3}{2} \Delta H _{3}$

(c) $\Delta _{i} H=\Delta H _{1}-\frac{\Delta H _{2}}{2}-\frac{3}{2} \Delta H _{2}$

(d) None

Question 22. Given that the enthalpy of formation of $\mathrm{H} _{2} \mathrm{O}$ is $-68 \mathrm{kcal} \mathrm{mol}^{-1}$, the enthalpy of formation of $\mathrm{OH}^{-}$ions will be

(a) $\quad-34 \mathrm{kcal} \mathrm{mol}^{-1}$

(b) $\quad-81.7 \mathrm{kcal} \mathrm{mol}^{-1}$

(c) $\quad-27.4 \mathrm{kcal} \mathrm{mol}^{-1}$

(d) $\quad-54.3 \mathrm{kcal} \mathrm{mol}^{-1}$

Question 23. $\mathrm{H} _{2}(\mathrm{~g})+1 / 2 \mathrm{O} _{2}(\mathrm{~g}) \rightarrow \mathrm{H} _{2} \mathrm{O}(\mathrm{I}) ; \Delta H^{\rho}=-68 \mathrm{kcal}$

$\mathrm{K}(\mathrm{s})+\mathrm{H} _{2} \mathrm{O}(\mathrm{I})+\mathrm{aq} \rightarrow \mathrm{KOH}(\mathrm{aq})+1 / 2 \mathrm{H} _{2} ; \Delta \mathrm{H}^{0}=-48 \mathrm{kcal}$

$\mathrm{KOH}(\mathrm{s})+\mathrm{aq} \rightarrow \mathrm{KOH}(\mathrm{aq}) ; \Delta H^{\circ} ;=-14 \mathrm{kcal}$

From the above data, the standard heat of formation of $\mathrm{KOH}$ in $\mathrm{kcal}$ is :

(a) $-68+48-14$

(b) $-68-48+14$

(c) $68-48+14$

(d) $68+48+14$

Question 24. Given: $\mathrm{CH} _{4}(\mathrm{~g})+\mathrm{Cl} _{2}(\mathrm{~g}) \rightarrow \mathrm{CH} _{3} \mathrm{Cl}(\mathrm{g})+\mathrm{HCl}(\mathrm{g}), \Delta H=-100.3 \mathrm{~kJ}$

Bond energies : $\mathrm{C}-\mathrm{H}=413 \mathrm{~kJ} \mathrm{~mol}^{-1}$

$\qquad \begin{aligned} & \mathrm{Cl}-\mathrm{Cl}=243 \mathrm{~kJ} \mathrm{~mol}^{-1} \\ & \mathrm{H}-\mathrm{Cl}=431 \mathrm{~kJ} \mathrm{~mol}^{-1} \end{aligned}$

The energy of $\mathrm{C}$ - $\mathrm{Cl}$ bond will be

(a) $ 225.0 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(b) $ 425.6 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(c) $ 325.3 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(d) $261.0 \mathrm{~kJ} \mathrm{~mol}^{-1}$

Question 25. The bond energies of $\mathrm{C}-\mathrm{C}, \mathrm{C}=\mathrm{C}, \mathrm{H} \mathrm{H}$ and $\mathrm{C}-\mathrm{H}$ linkages are $350,600,400$, and $410 \mathrm{~kJ}$ per mole respectively. The heat of hydrogenation of ethylene is

(a) $-170 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(b) $-260 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(c) $-400 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(d) $-450 \mathrm{~kJ} \mathrm{~mol}^{-1}$

Question 26. Enthalpy of $\mathrm{CH} _{4}+1 / 2 \mathrm{O} _{2} \longrightarrow \mathrm{CH} _{3} \mathrm{OH}$ is negative If enthalpy of combustion of methane and $\mathrm{CH} _{3} \mathrm{OH}$ are $x$ and $y$ respectively, then which relation is correct?

(a) $x>y$

(b) $ x<y$

(c) $x=y$

(d) $x \geq y$

Question 27. When 1 mole of crystalline $\mathrm{NaCl}$ is obtained from sodium and chlorine gas, $410 \mathrm{~kJ}$ of heat is released. The heat of sublimation of sodium metal is $108 \mathrm{~kJ} \mathrm{~mol}^{-1}$ and $\mathrm{Cl}-\mathrm{Cl}$ bond enthal py is 242 $\mathrm{kJ} \mathrm{mol}^{-1}$. If the ionization energy of $\mathrm{Na}$ is $493.0 \mathrm{~kJ} \mathrm{~mol}^{-1}$ and the electron affinity of chlorine is 368 $\mathrm{kJ} \mathrm{mol}^{-1}$, the lattice energy of $\mathrm{NaCl}$ is

(a) $ 764 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(b) $-764 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(c) $ 885 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(d) $-885 \mathrm{~kJ} \mathrm{~mol}^{-1}$

Question 28. The lattice enthalpy and hydration enthalpy of four compounds are given below:

The pair of compounds which is soluble in water is

(a) $P$ and $Q$

(b) $ Q$ and $R$

(c) $R$ and $S$

(d) $P$ and $R$

Question 29. Given the following data:

$\Delta _{4} H\left(\mathrm{C} _{2} \mathrm{H} _{4}\right)=12.5 \mathrm{kcal}$

Heat of atomisation of $\mathrm{C}=171 \mathrm{kcal}$

Heat of atomisation of $\mathrm{H}=521 \mathrm{kcal}$

Bond energy of $\mathrm{C}-\mathrm{H}$ bond $=99.3 \mathrm{kcal}$

What is $\mathrm{C}=\mathrm{C}$ bond energy?

(a) $ 140.7 \mathrm{kcal}$

(b) $ 36 \mathrm{kcal}$

(c) $40 \mathrm{kcal}$

(d) $76 \mathrm{kcal}$

Question 30. If an endothermic reaction occurs spontaneously at constant $\mathrm{T}$ and $\mathrm{P}$, then which of the following is true?

(a) $\Delta G>0$

(b) $\Delta H<0$

(c) $\Delta S>0$

(d) $\Delta S<0$

Question 31. For the given reaction $\mathrm{H} _{2}(\mathrm{~g})+\mathrm{Cl} _{2}(\mathrm{~g})+(\mathrm{aq}) \longrightarrow 2 \mathrm{H}^{+}(\mathrm{aq})+2 \mathrm{Cl}^{-}(\mathrm{aq}), \Delta \mathrm{G}^{0}=-262.4 \mathrm{~kJ}$ The value of Gibbs energy of formation $\left(\Delta _{i} G^{0}\right)$ for the ion $\mathrm{Cl}^{-}(\mathrm{aq})$, therefore, will be

(a) $\quad-131.2 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(b) $\quad+131.2 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(c) $\quad-262.4 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(d) $\quad+262.4 \mathrm{~kJ} \mathrm{~mol}^{-1}$

Question 32. Consider the reaction

$4 \mathrm{NO} _{2}(\mathrm{~g})+\mathrm{O} _{2}(\mathrm{~g}) \longrightarrow 2 \mathrm{~N} _{2} \mathrm{O} _{5}(\mathrm{~g}) \Delta _{\mathrm{r}} \mathrm{H}=-111 \mathrm{~kJ}$

If $\mathrm{N} _{2} \mathrm{O} _{5}(\mathrm{~s})$ is formed instead of $\mathrm{N} _{2} \mathrm{O} _{5}(\mathrm{~g})$ in the above reaction, the $\Delta _{4} \mathrm{Hvalue}$ will be : (given, $\Delta H$ of sublimation for $\mathrm{N} _{2} \mathrm{O} _{5}$ is $54 \mathrm{~kJ} \mathrm{~mol}^{-1}$ )

(a) $+219 \mathrm{~kJ}$

(b) $-219 \mathrm{~kJ}$

(c) $-165 \mathrm{~kJ}$

(d) $+54 \mathrm{~kJ}$

Question 33. Oxidizing power of chlorine in aqueous solution can be determined by the parameters indicated below:

$1 / 2 \mathrm{Cl} _{2}(\mathrm{~g}) \xrightarrow{1 / 2 \Delta _{\text {diss }} H^{p}} \mathrm{Cl}(\mathrm{g}) \xrightarrow{\Delta _{\mathrm{eq}} H^{p}} \mathrm{Cl}^{-}(\mathrm{g}) \xrightarrow{\Delta _{\mathrm{ndy}}} \mathrm{H}^{p} \mathrm{Cl}^{-(\mathrm{aq})}$

The energy involved in the conversion of $1 / 2 \mathrm{Cl} _{2}(\mathrm{~g})$ to $\mathrm{Cl}(\mathrm{aq})$

(Using the data, $\Delta _{\text {diss }} \mathrm{H} _{\mathrm{Cl} _{2}}^{\circ}=240 \mathrm{~kJ} / \mathrm{mol}, \Delta _{\mathrm{eq}} \mathrm{H} _{\mathrm{cl}}^{\circ}=-349 \mathrm{~kJ} / \mathrm{mol}, \Delta _{\mathrm{ndy}} \mathrm{H} _{\mathrm{Cl} 0}^{\circ}=-381 \mathrm{~kJ} / \mathrm{mol}$ ) will be

(a) $-610 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(b) $-850 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(c) $+120 \mathrm{~kJ} \mathrm{~mol}^{-1}$

(d) $+152 \mathrm{~kJ} \mathrm{~mol}^{-1}$

Question 34. Standard entropy of $\mathrm{X} _{2}, \mathrm{Y} _{2}$ and $\mathrm{XY} _{3}$ are 60,40 and $50 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}$, respectively. For the reaction $\frac{1}{2} \mathrm{X} _{2}+\frac{3}{2} \mathrm{Y} _{2} \longrightarrow \mathrm{XY} _{3} \Delta H=-30 \mathrm{KJ}$, to be at equilibrium, the temperature will be

(a) $500 \mathrm{~K}$

(b) $750 \mathrm{~K}$

(c) $1000 \mathrm{~K}$

(d) $1250 \mathrm{~K}$

Question 35. For a particular reversible reaction at temperature $T, \Delta H$ and $\Delta S$ were found to be both $+v e$. If $T$ e is the temperature at equilibrium, the reaction would be spontaneous when

(a) $T=T _{\mathrm{e}}$

(b) $T _{\mathrm{e}}>T$

(c) $ T>T _{\mathrm{e}}$

(d) $T _{\mathrm{e}}$ is 5 times $T$

Question 36. The value of enthalpy change $(\Delta H)$ for the reaction

$\mathrm{C} _{2} \mathrm{H} _{5} \mathrm{OH}(\mathrm{I})+3 \mathrm{O} _{2}(\mathrm{~g}) \quad 2 \mathrm{CO} _{2}(\mathrm{~g})+3 \mathrm{H} _{2} \mathrm{O}(\mathrm{I})$

at $27^{\circ} \mathrm{C}$ is $-1366.5 \mathrm{~kJ} \mathrm{~mol}^{-1}$. The value of internal energy change for the above reaction at this temperature will be :

(a) $-1364.0 \mathrm{~kJ}$

(b) $-1361.5 \mathrm{~kJ}$

(c) $-1371.5 \mathrm{~kJ}$

(d) $-1369.0 \mathrm{~kJ}$

Question 37. The incorrectexpression among the following is:

(a) $K=e-\frac{-\Delta G^{0}}{R T}$

(b) $\frac{\Delta G _{\text {system }}}{\Delta S _{\text {total }}}=-T$

(c) In isothermal process, $w _{\text {reversibe }}=-n R T \ln \frac{V _{f}}{V _{i}}$

(d) $\operatorname{In} K=\frac{\Delta H^{\rho}-T \Delta S^{0}}{R T}$

Question 38. A gas present in a cylinder fitted with a frictionless piston expands isothermally against a constant pressure of 1 bar from a volume of $2 \mathrm{~L}$ to $12 \mathrm{~L}$. In doing so, it absorbs $820 \mathrm{~J}$ heat from the surrounding. The change in internal energy during the process is :

(a) $-180 \mathrm{~J}$

(b) $-18 \mathrm{~J}$

(c) $+1820 \mathrm{~J}$

(d) $+920 \mathrm{~J}$

Question 39. A system containing an ideal gas was subjected to a number of changes as shown in the $p-V$ diagram. In the following cyclic process, A to F specify the type of change taking place from B to C. given that the

Temperature at $\mathrm{A}, \mathrm{B}$ and $\mathrm{F}=T _{1}$

Temperature at $\mathrm{C}, \mathrm{D}$ and $\mathrm{E}=T _{2}$ $T _{2}<T _{1}$

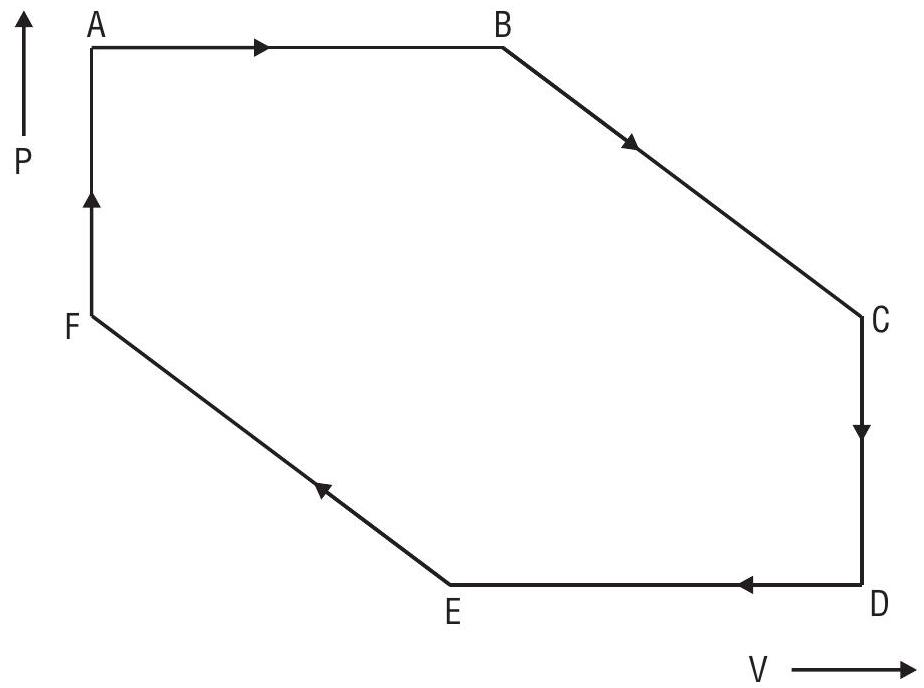
(a) Isochoric and isothermal (pressure falls)

(b) Adiabatic compression, temperature increases to $T _{1}$

(c) Adiabatic expansion, temperature fall to $\mathrm{T} _{2}$

(d) Isochoric and isothermal (pressure increases)

Question 40. In the reactions

I: $\mathrm{H} _{2} \rightarrow 2 \mathrm{H}$ $\qquad \qquad \qquad \Delta H=436 \mathrm{~kJ}$

II: $\mathrm{H} _{2}+\frac{1}{2} \mathrm{O} _{2} \rightarrow \mathrm{H} _{2} \mathrm{O}$ $\qquad \Delta H=-241.81 \mathrm{~kJ}$

III : $2 \mathrm{H}+1 / 2 \mathrm{O} _{2} \rightarrow \mathrm{H} _{2} \mathrm{O}$ $\quad \Delta H=$ ?

$\mathrm{H} _{2} \mathrm{O}$ can be formed either by II or III. Ratio of enthalpy change in III to II is :

(a) 2.8

(b) 1.2

(c) 0.36

(d) 0.82