General Idea

Matter can exist (mainly) in three states viz; solid, liquid and gas.

State of matter is determined by the nature of intermolecular forces, molecular interactions and thermal energy of particles.

Change in the physical state does not change the chemical properties of a substance.

Rates of Chemical reactions depend upon the physical state.

Physical laws govern the behavior of matter in different states.

Intermolecular Forces

Forces of attraction and repulsion between interacting particles (atoms and molecules).

Covalent bonding is not intermolecular force.

Van der Waals Forces

Attractive intermolecular forces.

These forces include dispersion forces or London forces, dipole-dipole forces and dipoleinduced dipole forces.

Ion-dipole forces are not van der Waals forces.

Dispersion forces or London Forces

Force of attraction between two temporary instantaneous dipoles.

There forces are always attractive.

Interaction energy $\propto 1/r^6$, where $r$ is the distance between the two particles.

Dipole-Dipole Forces

Present between the molecules possessing permanent dipoles.

For stationary polar molecules : interaction energy $\propto 1/r^3$

For rotating polar molecules : interaction energy $\propto 1/r^6$ where, $r=$ distance between polar molecules.

Hydrogen-bonding

Aspecial case of dipole-dipole interaction.

Exists in the molecules which are highly polar containing $\mathrm{N}-\mathrm{H},\mathrm{O}-\mathrm{H}$ or $\mathrm{H}-\mathrm{F}$ bonds.

Energy of $\mathrm{H}$-bond $\approx 10$ to $100\mathrm{kJ}{\mathrm{mol}}^{-1}$.

One of the important forces in proteins and nucleic acids.

It determines the structure and properties of many compounds.

Dipole-Induced Dipole Forces

Exists between polar molecules having permanent dipole and non-polar molecules.

Interaction Energy $\propto \frac{1}{r^6}$ where, $r=$ distance between two molecules.

Existence of the three states of matter - It is due to the balance between intermolecular forces and the thermal energy of the molecules.

Predominance of intermolecular interactions

Gas $\to$ liquid $\to$ solid

Predominance of thermal energy

Gas $⟵$ liquid $⟵$ solid

Comparison between gaseous and liquid states

Gaseous State	Liquid State
$\cdot$ Highly compressible	$\cdot$ Not compressible
$\cdot$ Much lower density than solids and liquids	$\cdot$ Denser than gases
$\cdot$ Volume and shape are not fixed	$\cdot$ Volume is fixed but shape is not
$\cdot$ Interactive forces are negligible	$\cdot$ Interactive forces are stronger than those in gaseous state.
$\cdot$ Behaviour of gases is governed by general laws of gases	$\cdot$ No such general laws exist.

The Gas Laws

1. Boyle’s Law ( $p-V$ relationship)

At constant $T\mathrm{\&}n$ (no. of moles)

$p\propto \frac{1}{V}$

$pV=$ Constant $$ or $\log p+\log V=\log K$

$$P_1{V}_1=P_2{V}_2$$

At a constant temperature, the pressure exerted by a fixed mass of a gas is inversely proportional to its volume.

Graphical Representation

Isotherm- line / plot between $p\mathrm{\&}V$ at constant temperature for a given amount ( $\mathrm{n}$ ) of the gas.

Isobar- line / plot between $V$ and $I$ at constant pressure ( $\mathrm{p}$ ) and $n$.

Isochore - line / plot between $p$ and $I$ at constant volume ( $V$ & $n$.

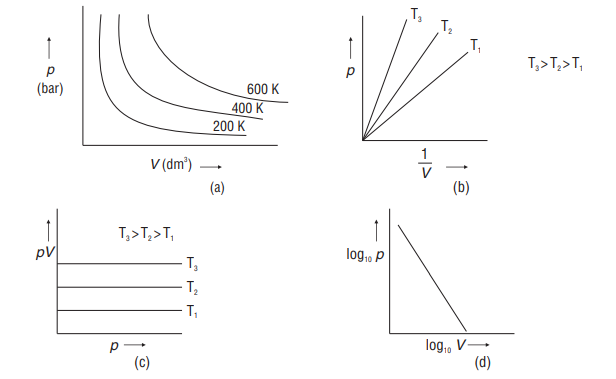
All the graphs shown above are isotherms

Note: At high pressures, gases deviate from Boyle’s law. So, a straight line is not obtained in the graph of $pvs(1/V)$.

Relation between density $(d)$ and pressure of a gas

$d=\frac{m}{v}$ and $pv=\mathrm{k}$ (Boyle’s law)

$d=\left(\frac{m}{k}\right)p={\mathrm{k}}^{\prime }p$

$\Rightarrow$ At a constant $\mathrm{T}$, density of a fixed mass of the gas is directly proportional to the pressure.

2.Charles’ Law ( $T$-Vrelationship):

At constant $P$ and $n$

$V\propto T$

$\frac{V}{T}=$ constant

i.e. $\frac{V_1}{T_1}=\frac{V_2}{T_2}$ or $\frac{V_2}{V_1}=\frac{T_2}{T_1}$

For a fixed mass of a gas, at a constant pressure, the volume of a gas is directly proportional to its absolute temperature.

Kelvin Temperature Scale or Absolute Temperature Scale

$$T=(273.15+t^{\circ }\mathrm{C})\mathrm{K}$$

Also, known as thermodynamic scale of temperature.

Graphical Representation

The graphs shown above are isobars

Absolute Zero (the lowest possible temperature) - The lowest hypothetical or imaginary temperature at which gases are supposed to occupy zero volume. Absolute Zero is equal to $-{273.15}^{\circ }\mathrm{C}$ $-{273.15}^{\circ }\mathrm{C}=0\mathrm{K}$

Note:

1. All gases obey Charles’ law at very low pressures and high temperatures.

2. Boyle’s and Charles’ law are examples of a limiting law, a law i.e. strictly true only in certain limit in this case $p\to 0$.

3.Gay Lussac’s Law ( $p-T$ relationship)

$p\propto T(V,n$ constant $)$

$\frac{p}{T}=$ constant

$\frac{p_1}{T_1}=\frac{p_2}{T_2}$

Graphical representation

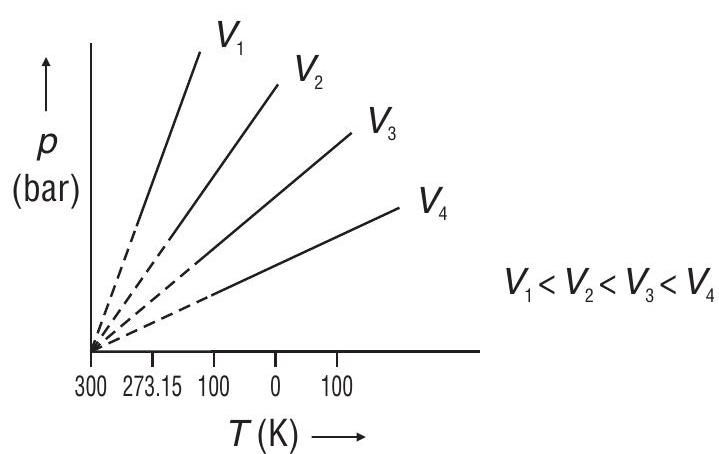
The graphs shown above are isochores.

4. Avogadro’s Law ( $V-\mathrm{n}$ Relationship) : At constant $p$ and $T$

$V\propto n$

$$V=kn$$

This law states that equal volumes of all gases under similar conditions of temperature and pressure contain equal number of molecules.

No. of molecules in one mole of a gas $=6.022\times {10}^{23}=N_{\mathrm{A}}$ (Avogadro constant).

Molar Volume-Volume occupied by one mole of each substance.

It contains the same number of molecules i.e. $N_{\mathrm{A}}$.

Molar Volume at different $T$ and $P$ are as follows :

Conditions	Temperature	Pressure	Molar Volume
NTP (Earlier also called STP)	$273.15\mathrm{K}$	$1\mathrm{atm}$	$22.4\mathrm{L}{\mathrm{mol}}^{-1}$
STP	$273.15\mathrm{K}$	$1\mathrm{bar}$	$22.7\mathrm{L}{\mathrm{mol}}^{-1}$
SATP	$298.15\mathrm{K}$	1 bar	$24.8\mathrm{L}{\mathrm{mol}}^{-1}$

STP : Standard Temperature and Pressure

NTP: Normal Temperature and Pressure

SATP: Standard Ambient Temperature and Pressure

No. of moles, $n=\frac{N}{N_{\mathrm{A}}}$ ( $N=$ no. of molecules $)$

or

$n=\frac{m}{M}\left(\begin{array}{l}m=\text{ mass of the gas }\mathrm{M}=\text{ molar mass }\end{array}\right)$

$V=k\frac{m}{M}$

$M=k\frac{m}{V}$

$M=kd$

where, $\mathrm{d}=$ density of the gas

$\Rightarrow$ density of a gas $\propto$ molar mass $(M)$

Ideal gas equation or Equation of State

It describes the state of any gas

Combine Boyle’s law, Charles’ law and Avogadro’s law

$V\propto \frac{1}{P}(\text{ at constant }T\mathrm{\&}n)\text{ Boyle’s Law }$

$V\propto T($ at constant $p\mathrm{\&}n)$ Charles Law

$V\propto n($ at constant $T\mathrm{\&}P)$ Avogadro’s Law

$V\propto \frac{n}{P}T$

$V=R\frac{nT}{P}$

$PV=nRT\Rightarrow$ It is the approximate equation of state of any gas and becomes increasingly exact as pressure of the gas approaches zero.

$\mathrm{R}=$ Universal Gas Constant.

5. Combined Gas Law:

$\frac{p_1{V}_1}{T_1}=\frac{p_2{V}_2}{T_2}$

Ideal gas equation in terms of density (Relationship between molar mass and density of a gas)

$p=\frac{dRT}{M}$ (Mis the molar mass, $d$ is the density)

Values of the gas constant:

$0.0821\mathrm{Latm}{\mathrm{K}}^{-1}{\mathrm{mol}}^{-1}$

$82.1{\mathrm{cm}}^3\mathrm{atm}{\mathrm{K}}^{-1}{\mathrm{mol}}^{-1}$

$0.083{\text{ bar dm }}^3{\mathrm{K}}^{-1}{\mathrm{mol}}^{-1}$

In the C.G.S. units

$8.314\times {10}^7\mathrm{ergs}{\mathrm{K}}^{-1}{\mathrm{mol}}^{-1}$

In S.I. units

$8.314\mathrm{J}{\mathrm{K}}^{-1}{\mathrm{mol}}^{-1}({10}^7\mathrm{erg}=\mathrm{I})$

In terms of calories

1.987 calories ${}^{-1}{\mathrm{mol}}^{-1}$ ( $4.184\mathrm{J}=$ I calorie)

Dalton’s Law of Partial Pressures :

Law is valid for non-reacting gases, at constant volume & constant Temperature.

$p_{\text{Total }}=p_1+p_2+p_3+—($ at constant $T,V)$

where, $p_{\text{Total }}=$ Total pressure exerted by the mixture of gases

$p_1,p_2,-\dots –=$ partial pressures of gases, 1,2 res.

Gases are generally collected over water and therefore are moist.

$p_{\text{drygas }}=p_{\text{Total }}$-Aqueous Tension

Aqueous Tension : Pressure exerted by saturated water vapour.

$p_{\text{Total }}$ :Total pressure of the moist gas.

Partial Pressure in terms of mole fraction

$p_i=x_i{p}_{\text{total }}$

where, $p_{\mathrm{i}}=$ Partial pressure of the ${\mathrm{i}}^{\text{th }}$ gas

$x_i=$ mole traction of the $i^{\text{th }}$ gas.

Different Pressure units and their relation

$1\mathrm{Pa}=1\mathrm{N}{\mathrm{m}}^{-2}$ or $1\mathrm{kg}{\mathrm{m}}^{-1}{\mathrm{s}}^{-2}$

1 bar $={10}^5\mathrm{Pa}$

$1\mathrm{atm}=101.325\mathrm{kPa}$

1 Torr $=(101325/760)\mathrm{Pa}=133.32\mathrm{Pa}$

$1\mathrm{mm}\mathrm{Hg}=1$ Torr $=133.322\mathrm{Pa}$

$1\mathrm{Psi}=6.894\mathrm{kPa}$

Psi = Pound per square inch

Standard pressure $=1$ bar

Normal pressure $=1$ atom

Graham’s Law of diffusion / effusion

At constant $T$ and $p$

$r\propto \sqrt{\frac{1}{d}}$

where $r=$ rate of diffusion $d=$ density of the gas

$\frac{r_1}{r_2}=\sqrt{\frac{d_2}{d_1}}$

As molar mass is directly proportional to the density of the gas at constant $T$ and $p$

$\frac{r_1}{r_2}=\sqrt{\frac{M_2}{M_1}}$

where $M_1$ and $M_2$ are the molar masses

If two gases are taken at different pressures, then, as greater the pressure, greater is the number of molecules hitting per unitarea, greater is the rate of diffusion.

$\frac{r_1}{r_2}=\frac{p_1}{p_2}\sqrt{\frac{d_2}{d_1}}=\frac{p_1}{p_2}\sqrt{\frac{M_2}{M_1}}$

For two gases undergoing diffusion at the same pressure but at two different temperatures:

$\frac{r_1}{r_2}=\sqrt{\frac{T_1{d}_2}{T_2{d}_1}}=\sqrt{\frac{T_1{M}_2}{T_2{M}_1}}$

Comparison of volumes of two different gases effused / diffused during the same time interval

$\frac{r_1}{r_2}=\frac{V_1/t}{V_2/t}=\frac{V_1}{V_2}=\sqrt{\frac{d_2}{d_1}}=\sqrt{\frac{M_2}{M_1}}$

where $V_1$ is the volume of gas 1 diffused / effused in time $t$ and $V_2$ is the volume of gas 2 diffused / effused in

the same time $t$ under the same conditions of temperature and pressure.

Comparison of times taken for effusion / diffusion of the same volume of two different gases

$\frac{r_1}{r_2}=\frac{V/t_1}{V/t_2}=\frac{t_2}{t_1}=\sqrt{\frac{d_2}{d_1}}=\sqrt{\frac{M_2}{M_1}}$

where, $t_1$ is the time taken for the gas 1 for effusion / diffusion of volume $V$ and $t_2$ is the time taken for gas 2

for effusion / diffusion of the same volume under the same conditions of temperature and pressure.

Kinetic Molecular Theory of Gases :

This theory helps us to understand the behavior of gases. This theory provides a microscopic model of gases.

Postulates / Assumptions

Gases consist of large number of very small identical particles (atoms or molecules) which are so for apart on the average that the actual volume of the molecules is negligible as compared to the empty space between them.

This explains the high compressibility of gases

No force of attraction between the particles of a gas.

Particles, within the container, are in ceaseless random motion during which they collide with each other and with the walls of the container.

All the collisions are perfectly elastic i.e. total energy of molecules before and after the collision remains same. The energy may, however, be transferred from one molecule to the other on collision.

Due to the bombardment of the molecules on the walls of the containing vessel, pressure is exerted by the gas on the walls of the containing vessel.

Particles of the gas move in straight line (i.e. it obeys Newton’s first law of motion).

At any particular time, different particles in the gas have different speeds and hence different kinetic energies.

Average K.E. of the gas molecules is directly proportional to the absolute temperature.

$$K.E. $\propto T$ or K.E. $\propto u^2$

$$$1/2\mathrm{m}{u}^2\propto T$

$$$u^2\propto T$

$$$u\propto \sqrt{T}$

i.e. Molecular velocity of any gas is directly protional to the square root of temperature.

Kinetic Gas Equation

$pV=\frac{1}{3}mN{c}^2$

$p=$ Pressure exerted by the gas, $V=$ volume of the gas

$m=$ Mass of each molecule, $N=$ total no. of gas molecules

$c=$ Root mean square speed $=U_{\text{ms }}$

Different Type of Speeds possessed by molecules

Most probable speed $\left(U_{mp}\right)$

speed possessed by maximum number of molecules.

$U_{\mathrm{mp}}=\sqrt{\frac{2RT}{M}}=\sqrt{\frac{2kT}{m}}$

$M=$ mass of 1 mole of molecules i.e. molar mass

$m=$ mass of 1 molecule

Average speed $\left(U_{\mathrm{av}}\right)$

Average speed possessed molecules of a gas at a given temperature.

$$U_{\mathrm{av}}=\sqrt{\frac{8RT}{\pi M}}=\sqrt{\frac{8kT}{\pi m}}$$

Root mean square speed $\left(U_{\mathrm{mm}}\right)$

Square root of mean of the squares of the speeds of different molecules of the gas at a given $T$

$$U_{\mathrm{rms}}=\sqrt{\frac{3RT}{M}}=\sqrt{\frac{3kT}{m}}$$

Comparison of different speeds

$$\begin{array}{rl}& U_{\mathrm{ms}}:U_{\mathrm{av}}:U_{\mathrm{mp}}=1:0.92:0.82\\ & U_{\mathrm{ms}}>U_{\mathrm{av}}>U_{\mathrm{mp}}\end{array}$$

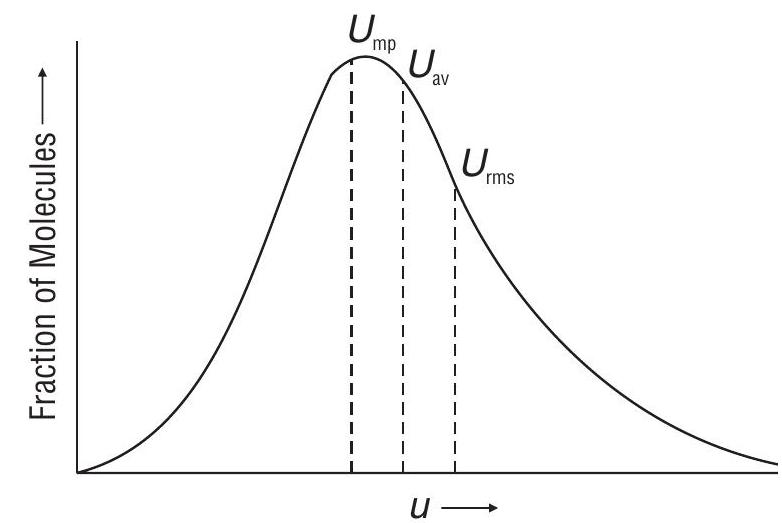
Maxwell - Boltzmann distribution of molecular speeds

Another relation between speeds

$U_{\mathrm{mp}}:U_{\mathrm{av}}:U_{\mathrm{ms}}=1:1.128:1.224$

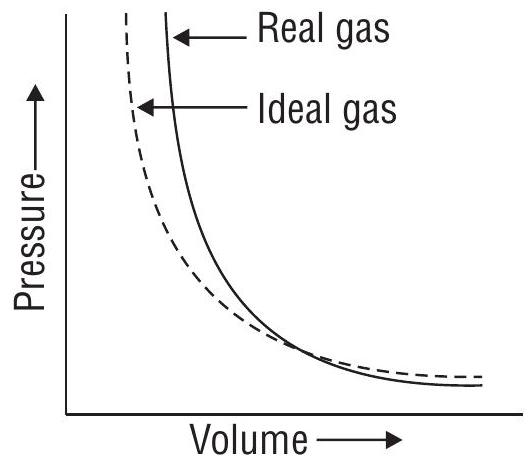
Ideal and Real Gas

Ideal gas

A gas which obeys ideal gas equation, $pV=nRT$ under all conditions of temperature and pressure. No gas obeys ideal gas equation under all conditions of temperature and pressure.

Real gas

A gas which obey gas laws at low pressure and high temperature. All gases are real gases.

Causes of Deviation from Ideal Behaviour

Assumptions of Kinetic theory of gases which do not hold good in all conditions:

1. The intermolecular force of attraction between gaseous molecules is negligible.

2. The volume occupied by the gas molecules is negligible in comparison to the total volume of the gas.

Compressibility Factor $(Z)$ - Gives the extent to which real gas deviates from ideal behaviour.

$Z=\frac{pV}{nRT}$

$$ For 1 mole of gas, $Z=\frac{PV}{RT}$

$Z=1\Rightarrow$ Gas is ideal; $pV=nRT$

$Z=1\Rightarrow$ Gas is real; $PV\ne nRT$

$Z<1\Rightarrow$ Gas show - ve deviation and it is more compressible than ideal gas (usually at low pressure).

$Z>1\Rightarrow$ Gas shows +ve deviation and it is less compressible than ideal gas (usually at high pressure).

Plot : variation of $Z$ with $p$ for some gases

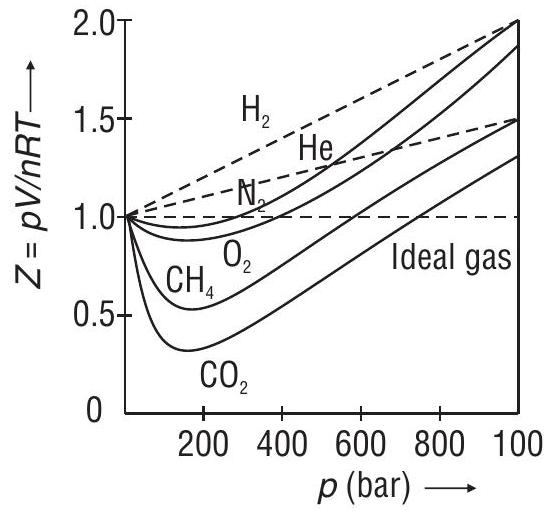
The value of $Z$ at very low pressure is approximately 1.

Plot of $pvsV$ for ideal and real gases

The variation of $Z$ with different temperatures $T_4>T_3>T_2>T_1$

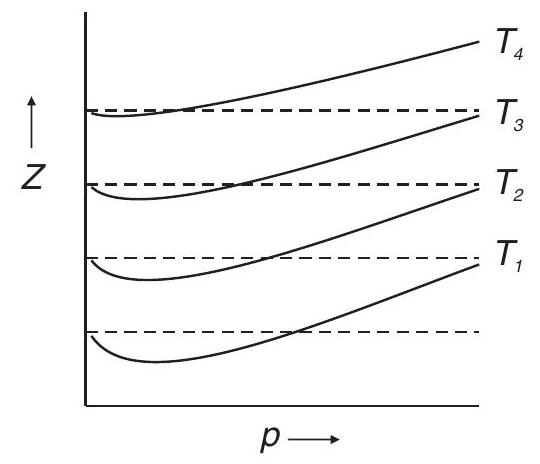
The deviation from ideal behavior becomes less and less with increase in temperature.

Boyle’s temperature :

Temperature at which a real gas obeys ideal gas equation over an appreciable range of pressure.

Significance of compressibility factor $(Z)$

$Z=\frac{p{V}_{\text{red }}}{nRT}$

for the ideal gas, $V_{\text{ideal }}=\frac{nRT}{p}$

$Z=\frac{V_{\text{real }}}{V_{\text{iteal }}}$

$Z$ is the ratio of actual volume of a gas to the calculated volume of an equal amount of an ideal gas.

van der Waals equation

This equation explains the behavior of real gases (not completely).

It considered two facts 1. Attraction between molecules

$$2. Volume of molecules is not negligible

$(P+\frac{a{n}^2}{V^2})(V-nb)=nRT$

Corrected Corrected

Pressure Volume

I Term : $p_{\text{iteal }}=p_{\text{real }}+\frac{a{n}^2}{V^2}$

II Term: Corrected volume $=V-nb$

where, $nb=$ total effective volume occupied by the molecules

Also, $b=4\mathrm{V}$, known as excluded volume or co-volume

where, $v=$ volume of a gas molecule.

Significance of van der Waals constants

$a$ : It is a measure of magnitude of intermolecular attractive forces within the gas.

Greater the value of ‘a’, stronger are the intermolecular forces of attraction and gas can be liquefied more easily.

$b$ : It is a measure of the effective size of the gas molecules.

It is related to incompressible volume of the molecules.

Units of ‘a’ and ’ $b$ '

$a=\frac{p\times V^2}{n^2}=\mathrm{atm}{\mathrm{L}}^2{\mathrm{mol}}^{-2}$ or bar ${\mathrm{dm}}^6{\mathrm{mol}}^{-2}$

$b=\frac{V}{n}=\mathrm{L}{\mathrm{mol}}^{-1}$ or ${\mathrm{dm}}^3{\mathrm{mol}}^{-1}$

Explanation of Behaviour of Real Gases

At very low pressures or at very high temperatures

$pV=nRT$

Gases behave like ideal gases

At moderate pressures, for 1 mole of a gas

$$\begin{array}{rl}& \frac{pV}{RT}=1-\frac{a}{RTV}\\ & Z=1-\frac{a}{RTV}\end{array}$$

$$Z<1$$

• At high pressures, for 1 mole of a gas

$$\begin{array}{rl}& \frac{PV}{RT}=1+\frac{Pb}{RT}\\ & Z=1+\frac{pb}{RT}& Z>1\end{array}$$

Exceptional behavior of ${\mathrm{H}}_2$ and $\mathrm{He}$ :

This is due to the fact that intermolecular forces of attraction in them are negligible.

Value of ’ $a$ ’ is very small and thus $\frac{a}{V^2}$ is negligible

$$\begin{array}{rl}& p(V-b)=RT\\ & pV=RT+Pb\\ & \frac{PV}{RT}=1+\frac{Pb}{RT}\end{array}$$

$Z>1$ (always, no dip in the curve of $Z$ vs $p$ ).

Liquefaction of Gases :

A gas can be liquefied by decreasing the temperature or by increasing the pressure or by the combination of both.

Critical constants $T_{\mathrm{c}},p_{\mathrm{c}}$ and $V_{\mathrm{c}}$

Critical Temperature, $T_{\mathrm{c}}$ :

Temperature above which a gas cannot be liquefied howsoever high the pressure may be.

It the maximum temperature at which a substance can exist as liquid.

$$T_{\mathrm{c}}=\frac{8a}{27Rb}$$

Critical Pressure, ${\mathit{P}}_{\mathrm{c}}$ :

Minimum pressure required to liquefy the gas at its critical temperature.

$P_{\mathrm{c}}=\frac{a}{27b^2}$

Critical Volume, $V_{\mathrm{c}}$ :

Volume occupied by one mole of a gas at its critical temperature and critical pressure.

$V_{\mathrm{c}}=3\mathrm{b}$

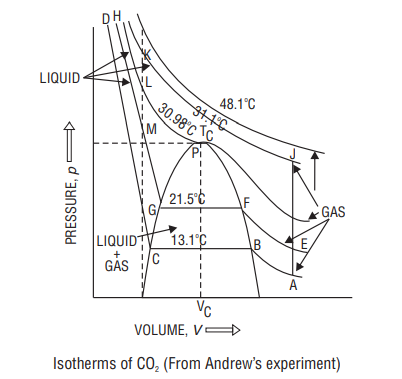
Andrew’s Isotherms: Isotherms of ${\mathrm{CO}}_2$ at different temperatures

At $\mathrm{A}\left({13.1}^{\circ }\mathrm{C}\right){\mathrm{CO}}_2$ exists as gas

On increasing pressure, at B liquefaction starts.

$AtC$, liquefaction is complete.

After that, increase in pressure has little effect on volume, since liquids have low compressibility.

Above ${30.98}^{\circ }\mathrm{C}$, gas cannot be liquified howsoever high pressure may be applied.

Point $\mathrm{P}\left({30.98}^{\circ }\mathrm{C}\right)$ is the critical temperature.

Difference between vapour and gas

Above critical temperature ${\mathrm{CO}}_2$ is a gas and below critical temperature, it is vapour. Also, vapour can be liquified by compression alone while a gas must be first cooled to a temperature below its critical temperature and then compressed.

Liquid State

Vapour Pressure

pressure exerted by the vapour present above the liquid in equilibrium with the liquid at that temperature.

Factors affecting vapour pressure

i. Nature of liquid - Weaker the intermolecular forces of attraction in a liquid, higher is the vapour pressure.

ii. Temperature-Vapour pressure increases with increase in temperature.

Normal boiling point-Boiling temperature under 1 atm pressure

Standard boiling point-Boiling temperature under 1 bar pressure

For ${\mathrm{H}}_2\mathrm{O}$ : Normal boiling point $={100}^{\circ }\mathrm{C}(373\mathrm{K})$

Standard boiling point $={99.6}^{\circ }\mathrm{C}(372.6\mathrm{K})$

Surface Tension

The force acting per unit length perpendicular to the imaginary line drawn on the surface of liquid and towards the liquid side.

S.I. unit $=\mathrm{N}{\mathrm{m}}^{-1}$ : CGS unit $=$ dyne ${\mathrm{cm}}^{-1}$

$1\mathrm{N}{\mathrm{m}}^{-1}=1000$ dyne ${\mathrm{cm}}^{-1}$

Factors affecting surface tension

i. Nature of liquid - Stronger the intermolecular forces of attraction in a liquid, higher is the surface tension.

ii. Temperature-Surface tension decreases with increase in temperature.

Consequences of surface tension

i. Spherical shape of liquid drops - Surface tension tries to decrease the surface area of a liquid to minimum. Since for a given volume of liquid, sphere has the minimum surface area so liquid drops acquire spherical shape.

ii. Capillary action - Rise of liquid in capillary is due to the surface tension which pushes the liquid into the capillary tube.

Shape of Meniscus

Water has a concave meniscus whereas mercury has a convex meniscus : In case of water, adhesive forces are stronger than cohesive forces. In case of mercury, cohesive forces are stronger than adhesive forces.

Cohesive forces - Attractive forces existing between molecules of same substance e.g. between water molecules or mercury molecules.

Adhesive forces - Attractive forces existing between molecules of different substances like water and glass or mercury and glass.

Surface Energy

Energy required to increase the surface area of the liquid by one unit.

S.I. Unit $={\mathrm{Jm}}^{-2}$

$=\eta {\mathrm{m}}^{-1}$

Dimensionally, surface tension and surface energy are same. Both have the same units.

Viscosity

A measure of friction / resistance to flow of liquid.

$f=\eta A\frac{du}{dx}$

where, $f=$ force of friction between 2 layers

$A=$ area of layer

$\frac{\mathrm{d}u}{\mathrm{d}x}=$ velocity gradient

$\eta =$ coefficient of viscosity

S.I. units of $\eta ={\mathrm{Nm}}^{-2}\mathrm{s}$ or Pas or $\mathrm{kg}{\mathrm{m}}^{-1}{\mathrm{s}}^{-1}$

C.G.S unit of $\eta =$ dynes ${\mathrm{cm}}^{-2}$ s or poise or ${\mathrm{cm}}^{-1}{\mathrm{s}}^{-1}$

1 Pas $=10$ poise

Factors affecting viscosity

Nature of liquid - stronger the intermolecular forces of attraction, higher is the viscosity.

Temperature-viscosity decreases on increasing the temperature.

Solved Examples

Question 1. A sample of gas occupies $100\mathrm{mL}$ at ${27}^{\circ }\mathrm{C}$ and $740\mathrm{mm}$ pressure. When its volume is changed to $80\mathrm{mL}$ at $740\mathrm{mm}$ pressure, the temperature of the gas will be

(a) ${21.6}^{\circ }\mathrm{C}$

(b) ${240}^{\circ }\mathrm{C}$

(c) $-{33}^{\circ }\mathrm{C}$

(d) ${89.5}^{\circ }\mathrm{C}$

Show Answer

Solution: (c)

Since, Pressure is same

According to Charles law

$$\begin{array}{rl}& \frac{V_1}{T_1}=\frac{V_2}{T_2}(T_1=27+273=300\mathrm{K})\\ & \frac{100}{300}=\frac{80}{T_2}\\ & T_2=240\mathrm{K}=240-273=-{33}^{\circ }\mathrm{C}\end{array}$$

Question 2. Pressure of a mixture of $4\mathrm{g}$ of ${\mathrm{O}}_2$ and $2\mathrm{g}$ of ${\mathrm{H}}_2$ confined in a bulb of 1 litre at $0^{\circ }\mathrm{C}$ is

(a) $25.215\mathrm{atm}$

(b) $31.205\mathrm{atm}$

(c) $45.215\mathrm{atm}$

(d) $15.210\mathrm{atm}$

Show Answer

Solution: (a)

According to the Dalton’s law of partial pressures

$p_{\mathrm{T}}=p_1+p_2$

$p_1=$ Partial pressure of ${\mathrm{O}}_2$

$p_2=$ Partial Pressure of ${\mathrm{H}}_2$

$p_{\mathrm{T}}=$ Pressure of the mixture or total pressure

$p_{\mathrm{T}}=(n_1+n_2)\frac{RT}{V}$ $=(\frac{4}{32}+\frac{2}{2})\frac{0.0821\times 273}{1}$

$=(\frac{1}{8}+1)22.413$

$p_{\mathrm{T}}=25.215\mathrm{atm}$

Question 3. A $1:1$ mixture (by weight) of hydrogen and helium is enclosed in a one litre flask kept at $0^{\circ }\mathrm{C}$. Assuming ideal behavior, the partial pressure of helium is found to be $0.42\mathrm{atm}$. Then the concentration of hydrogen would be

(a) $0.0375\mathrm{M}$

(b) $0.028\mathrm{M}$

(c) $0.0562\mathrm{M}$

(d) $0.0187\mathrm{M}$

Show Answer

Solution: (a)

1:1 mixture by weight of ${\mathrm{H}}_2$ and $\mathrm{He}$ means if $4\mathrm{g}$ each of $\mathrm{He}$ and ${\mathrm{H}}_2$ are taken, 1 mole of $\mathrm{He}$ is present then number of moles of ${\mathrm{H}}_2$ will be 2 .

$n_{\mathrm{He}}=n_1=1$ and $n_{{\mathrm{H}}_2}=n_2=2$

For He: $p_1=\frac{n_{1}RT}{V}$

For ${\mathrm{H}}_2:p_2=\frac{n_{2}RT}{V}$

According to Dalton’s law of partial pressure $p_{\mathrm{T}}=p_1+p_2$

$=(n_1+n_2)\frac{RT}{V}$

$\frac{p_1}{p_{\mathrm{T}}}=\frac{n_1}{n_1+n_2}$

$\frac{0.42}{p_{\mathrm{T}}}=\frac{1}{3}$

$p_{\mathrm{T}}=1.26\mathrm{atm}$

Using, $p_{\mathrm{T}}$, total number of moles $(n)$ can be found out

$1.26=n\times 0.0821\times 273$

$n=0.0562$

Number of moles of ${\mathrm{H}}_2=n_2=\frac{2}{3}\times 0.0562=0.0375\mathrm{mol}$

Volume $=1\mathrm{L}$

Therefore, concentration of ${\mathrm{H}}_2=0.0375\mathrm{M}$

Question 4. A stockroom supervisor measured the contents of a partially filled $25.0\mathrm{L}$ acetone drum on a day when the temperature was ${18}^{\circ }\mathrm{C}$ and atmospheric pressure was $790\mathrm{mm}\mathrm{Hg}$ and found that 16.5 $\mathrm{L}$ of the solvent remained. After sealing the drum a student assistant dropped the drum while carrying it upstairs to the chemistry laboratory. The drum was dented and its internal volume decreased to $21.0\mathrm{L}$, if the vapour pressure of acetone at ${18}^{\circ }\mathrm{C}$ is $400\mathrm{mm}\mathrm{Hg}$, the total pressure inside the drum after the accident was

(a) $736.66\mathrm{mm}\mathrm{Hg}$

(b) $157.85\mathrm{mm}\mathrm{Hg}$

(c) $1136.66\mathrm{mm}\mathrm{Hg}$

(d) $557.85\mathrm{mm}\mathrm{Hg}$

Show Answer

Solution: (c)

Vapour pressure of acetone remains unchanged at $400\mathrm{mm}\mathrm{Hg}$.

Only the partial pressure of air ( $p_{\text{air }}=p_{\text{total }}-p_{\text{acetone }}$ ) is affected by the change in the internal volume of the container.

$V_{\text{air }}$ (before) $=25.0-16.5=8.5\mathrm{L}$

$V_{\text{air }}($ after $)=21.0-16.5=4.5\mathrm{L}$

$p_{\text{air }}$ (before) $=790-400=390\mathrm{mm}\mathrm{Hg}$

Partial pressure of air ( $p_{\text{air }}$ ) after the accident can be calculated using the Boyle’s law.

$p_{\text{air }}{V}_{\text{air }}$ (Before) $)=p_{\text{air }}{V}_{\text{air }}$ (after)

$390\times 8.5=P_{\text{air }}\times 4.5$

$p_{\text{air }}=736.66\mathrm{mm}\mathrm{Hg}$

$p_{\mathrm{T}}=p_{\text{air }}+p_{\text{actone }}=736.66+400$

$=1136.66\mathrm{mm}\mathrm{Hg}$

Question 5. If ${10}^{-4}{\mathrm{dm}}^3$ of water is introduced into a $1.0{\mathrm{dm}}^3$ flask at $300\mathrm{K}$, how many moles of water are in the vapour phase when equilibrium is established (Given : Vapur pressure of ${\mathrm{H}}_2\mathrm{O}$ at $300\mathrm{K}$ is 3170 $\mathrm{Pa};\mathrm{R}=8.314\mathrm{J}{\mathrm{K}}^{-1}{\mathrm{mol}}^{-1}$ )

(a) $1.27\times {10}^{-3}\mathrm{mol}$

(b) $5.56\times {10}^{-3}\mathrm{mol}$

(c) $1.53\times {10}^{-3}\mathrm{mol}$

(d) $4.46\times {10}^{-3}\mathrm{mol}$

Show Answer

Solution: (a)

The value of volume used should be the volume of the container $\left(1.0{\mathrm{dm}}^3\right)$ as the number of moles of water in the vapour phase is to be calculated and the volume of water is negligible small $\left({10}^{-4}{\mathrm{dm}}^3\right)$

$pV=nRT(1{\mathrm{dm}}^3={10}^{-3}{\mathrm{m}}^3)$

$n=\frac{3170\times 1.0\times {10}^{-3}}{8.314\times 300}$

$=1.27\times {10}^{-3}\mathrm{mol}$

Practice Questions

Question 1. If two moles of an ideal gas at $546\mathrm{K}$ occupy a volume of 44.8 litres, the pressure must be

(a) $2\mathrm{atm}$

(b) 3 atm

(c) $4\mathrm{atm}$

(d) $1\mathrm{atm}$

Show Answer

Answer: (a)

Question 2. The volume of a gas is $100\mathrm{mL}$ at ${100}^{\circ }\mathrm{C}$. If pressure remains constant then at what temperature it will be $200\mathrm{mL}$ ?

(a) ${200}^{\circ }\mathrm{C}$

(b) ${473}^{\circ }\mathrm{C}$

(c) ${746}^{\circ }\mathrm{C}$

(d) ${50}^{\circ }\mathrm{C}$

Show Answer

Answer: (a)

Question 3. $120\mathrm{g}$ of an ideal gas of molar mass $40\mathrm{g}\mathrm{mole}$ are confined to a volume of $20\mathrm{L}$ at $400\mathrm{K}\mathrm{Using}\mathrm{R}$ $=0.0821\mathrm{L}\mathrm{atm}{\mathrm{K}}^{-1}{\mathrm{mole}}^{-1}$, the pressure of the gas is

(a) $4.90\mathrm{atm}$

(b) $4.92\mathrm{atm}$

(c) $5.02\mathrm{atm}$

(d) $4.96\mathrm{atm}$

Show Answer

Answer: (b)

Question 4. Pure hydrogen sulphide is stored in a tank of 100 litre capacity at ${20}^{\circ }\mathrm{C}$ and $2\mathrm{atm}$ pressure. The mass of the gas will be

(a) $34\mathrm{g}$

(b) $340\mathrm{g}$

(c) $282.4\mathrm{g}$

(d) $28.24\mathrm{g}$

Show Answer

Answer: (c)

Question 5. At $0^{\circ }\mathrm{C}$ and one atm pressure, a gas occupies $100\mathrm{cc}$. If the pressure is increased to one and a half-time and temperature is increased by one-third of given temperature, then final volume of the gas will be

(a) $80\mathrm{cc}$

(b) $88.9\mathrm{cc}$

(c) $66.7\mathrm{cc}$

(d) $100\mathrm{cc}$

Show Answer

Answer: (b)

Question 6. Molecular weight of a gas that diffuses twice as rapidly as the gas with molecular weight 64 is

(a) 16

(b) 8

(c) 64

(d) 6.4

Show Answer

Answer: (a)

Question 7. If rate of diffusion of $A$ is 5 times that of $B$, what will be the density ratio of $A$ and $B$ ?

(a) $1/25$

(b) $1/5$

(c) 25

(d) 4

Show Answer

Answer: (a)

Question 8. At what temperature, the rate of effusion of ${\mathrm{N}}_2$ would be 1.625 times that of ${\mathrm{SO}}_2$ at ${50}^{\circ }\mathrm{C}$ ?

(a) $110\mathrm{K}$

(b) $173\mathrm{K}$

(c) $373\mathrm{K}$

(d) $273\mathrm{K}$

Show Answer

Answer: (c)

Question 9. Equal weights of ethane and hydrogen are mixed in an empty container at ${25}^{\circ }\mathrm{C}$. The fraction of the total pressure exerted by hydrogen is

(a) $1:2$

(b) $1:1$

(c) $1:16$

(d) $15:1$

Show Answer

Answer: (d)

Question 10. $160\mathrm{mL}$ of a gas are collected over water at ${25}^{\circ }\mathrm{C}$ and $745\mathrm{mm}\mathrm{Hg}$. If aqueous tension at ${25}^{\circ }\mathrm{C}$ is $23.8\mathrm{mm}\mathrm{Hg}$, then pressure of dry gas at ${25}^{\circ }\mathrm{C}$ is :

(a) $768.8\mathrm{mm}\mathrm{Hg}$

(b) $760\mathrm{mm}\mathrm{Hg}$

(c) $721.2\mathrm{mm}\mathrm{Hg}$

(d) $600\mathrm{mm}\mathrm{Hg}$

Show Answer

Answer: (c)

Question 11. If $500\mathrm{mL}$ of a gas A at $1000\mathrm{Torr}$, and $1000\mathrm{mL}$ of gas B at 800 Torr are placed in a $2\mathrm{L}$ container, the final pressure will be

(a) 100 Torr

(b) 650 Torr

(c) 1800 Torr

(d) $2400\mathrm{mm}\mathrm{Hg}$

Show Answer

Answer: (b)

Question 12. Which of the following is not the postulate of the kinetic theory of gases?

(a) Gas molecules are in a permanent state of random motion.

(b) Pressure of gas is due to molecular impacts on the walls.

(c) The molecules are perfectly elastic.

(d) The molecular collisions are elastic.

Show Answer

Answer: (c)

Question 13. Maximum deviation from ideal gas is expected from

(a) ${\mathrm{CH}}_4(\mathrm{g})$

(b) ${\mathrm{NH}}_3(\mathrm{g})$

(c) ${\mathrm{H}}_2(\mathrm{g})$

(d) ${\mathrm{N}}_2(\mathrm{g})$

Show Answer

Answer: (b)

Question 14. The behavior of real gases approach ideal behavior at

(a) low temperature, low pressure

(b) high temperature, high pressure

(c) low temperature, high pressure

(d) high temperature, low pressure

Show Answer

Answer: (d)

Question 15. At extremely low pressure the van der Waals equation for one mole of a gas may be written as:

(a) $pV=RT+pb$

(b) $(p+a/V_2)(V-b)=RT$

(c) $pV=RT-a/V$

(d) $pV=RT$

Show Answer

Answer: (d)

Question 16. The value of van der Waals constant ’ $a$ ’ for ${\mathrm{N}}_2$ and ${\mathrm{NH}}_3$ are 1.39 and $4.17\mathrm{atm}{\mathrm{L}}^2{\mathrm{mol}}^{-2}$ respectively. If these two gases have the same value of constant ’ $b$ ’ then under similar conditions:

(a) The pressure exerted by ${\mathrm{N}}_2$ gas is more than that of ${\mathrm{NH}}_3$

(b) The pressure exerted by nitrogen is less than that of ${\mathrm{NH}}_3$

(c) Both exertequal pressure

(d) None of these

Show Answer

Answer: (a)

Question 17. Positive deviation from ideal gas behavior takes places because of

(a) Molecular interaction between atoms and $pV/nRT>1$

(b) Molecular interaction between atoms and $pV/nRT<1$

(c) Finite size of the atoms and $pV/nRT>1$

(d) Finite size of the atoms and $pV/nRT<1$

Show Answer

Answer: (a)

Question 18. Consider the following plot

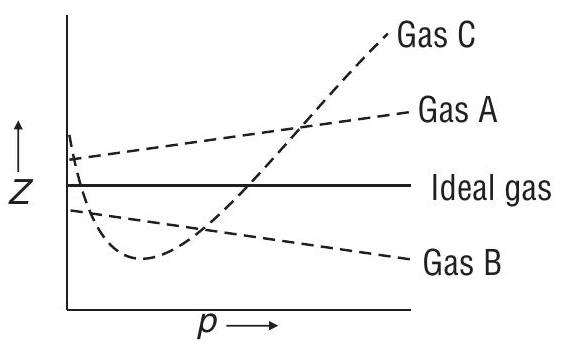
Which of the following statement is wrong?

(a) For a gas $A,a=0$, and $Z$ will linearly depend on pressure.

(b) For gas $\mathrm{B},b=0$ and $Z$ will linearly depend on pressure.

(c) Gas $C$ is a real gas and we can find ’ $a$ ’ and ’ $b$ ’ if intersection data is given.

(d) All van der Waals gases will behave like gas $\mathrm{C}$ and give positive slope at high pressure.

Show Answer

Answer: (c)

Question 19. Critical temperatures of ${\mathrm{H}}_2\mathrm{O},{\mathrm{NH}}_3,{\mathrm{CO}}_2$ and ${\mathrm{O}}_2$ are $647\mathrm{K},405.6\mathrm{K},304.10\mathrm{K}$ and $154.2\mathrm{K}$ respectively. If the cooling starts from $500\mathrm{K}$ to their critical temperature, the gas that liquefies first is

(a) ${\mathrm{H}}_2\mathrm{O}$

(b) ${\mathrm{NH}}_3$

(c) ${\mathrm{CO}}_2$

(d) ${\mathrm{O}}_2$

Show Answer

Answer: (a)

Question 20. The compressibility factor for a real gas a thigh pressure is

(a) 1

(b) $1+pb/RT$

(c) $1-pb/RT$

(d) $1+RT/pb$

Show Answer

Answer: (b)

Question 21. For one mole of a van der Waals gas when $b=0$ and $T=300\mathrm{K}$, the $pV\mathrm{vs}1/V$ plot is shown below. The value of the van der Waals’ constant $a$ atm ${\mathrm{L}}^2{\mathrm{mol}}^{-2}$

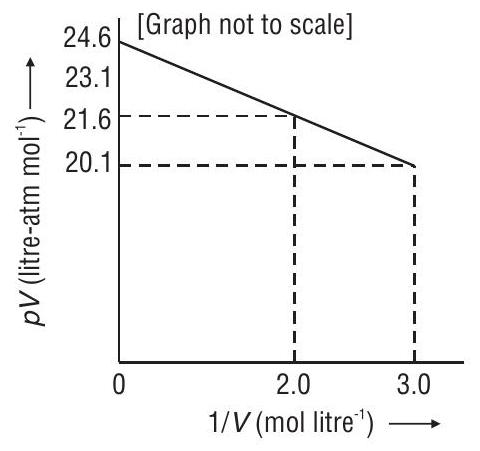
(a) 1.0

(b) 4.5

(c) 1.5

(d) 3.0

Show Answer

Answer: (c)

Question 22. ‘a’ and ’ $b$ ’ are van der Waals constants for gases. Chlorine is more easily liquefied than ethane because

(a) aand $b$ for ${\mathrm{Cl}}_2>a$ and $b$ for ${\mathrm{C}}_2{\mathrm{H}}_6$

(b) aand $b$ for ${\mathrm{Cl}}_2<$ aand $b$ for ${\mathrm{C}}_2{\mathrm{H}}_6$

(c) afor ${\mathrm{Cl}}_2<$ afor ${\mathrm{C}}_2{\mathrm{H}}_6$ but $b$ for ${\mathrm{Cl}}_2>$ bfor ${\mathrm{C}}_2{\mathrm{H}}_6$

(d) afor ${\mathrm{Cl}}_2>$ afor ${\mathrm{C}}_2{\mathrm{H}}_6$ but $b$ for ${\mathrm{Cl}}_2<b$ for ${\mathrm{C}}_2{\mathrm{H}}_6$

Show Answer

Answer: (d)

Question 23. The compressibility of a gas is less than unity at NTP.

(a) $V_{\mathrm{m}}>22.4\mathrm{L}$

(b) $V_{\mathrm{m}}<22.4\mathrm{L}$

(c) $V_{\mathrm{m}}=22.4\mathrm{L}$

(d) $V_{\mathrm{m}}=44.8\mathrm{L}$

Show Answer

Answer: (b)

Question 24. A gas can be liquefied

(a) above its critical temperature

(b) at its critical temperature

(c) below its critical temperature

(d) at any temperature

Show Answer

Answer: (c)

Question 25. On heating a liquid, its viscosity

(a) increases

(b) decreases

(c) remains same

(d) is reduced to zero

Show Answer

Answer: (b)

Question 26. The surface tension of which of the following liquid is maximum?

(a) ${\mathrm{C}}_2{\mathrm{H}}_5\mathrm{OH}$

(b) ${\mathrm{CH}}_3\mathrm{OH}$

(c) ${\mathrm{H}}_2\mathrm{O}$

(d) ${\mathrm{C}}_6{\mathrm{H}}_6$

Show Answer

Answer: (c)

Question 27. Choose the incorrect statement in the following:

(a) Surface tension is the force acting per unit length perpendicular to the line drawn on the surface of the liquid.

(b) Surface tension of a liquid increases with increase in temperature.

(c) The Sl unit of surface tension is ${\mathrm{Jm}}^{-2}$.

(d) Viscosity is a measure of resistance for the flow of liquid.

Show Answer

Answer: (b)

Question 28. The gas with the highest critical temperature is

(a) ${\mathrm{H}}_2$

(b) $\mathrm{He}$

(c) ${\mathrm{N}}_2$

(d) ${\mathrm{CO}}_2$

Show Answer

Answer: (d)

Question 29. Which of the following property of water be used to explain the spherical shape of rain droplets?

(a) viscosity

(b) surface phenomenon

(c) critical phenomena

(d) vapour pressure

Show Answer

Answer: (b)

Question 30. The SI unit of viscosity coefficient $(\eta )$ is

(a) Pascal

(b) ${\mathrm{Nm}}^{-2}\mathrm{s}$

(c) $\mathrm{kg}{\mathrm{m}}^{-2}\mathrm{s}$

(d) ${\mathrm{Nm}}^{-2}$

Show Answer

Answer: (b)

Question 31. How will the viscosity of liquid be affected by the increase in temperature?

(a) Increase

(b) No effect

(c) Decrease

(d) No regular pattern will be followed

Show Answer

Answer: (c)

Question 32. The van der Waals constant ’ $a$ ’ for different gases have been given as :

$\begin{array}{lllll}\text{Gas}& {\mathrm{O}}_2& {\mathrm{N}}_2& {\mathrm{CH}}_4& {\mathrm{NH}}_3\\ a\left(\text{atm L}{\mathrm{mol}}^2\right)& 1.36& 1.39& 2.15& 4.17\end{array}$

(a) ${\mathrm{O}}_2$

(b) ${\mathrm{N}}_2$

(c) ${\mathrm{CH}}_4$

(d) ${\mathrm{NH}}_3$

Show Answer

Answer: (d)

Question 33. The incorrect statement among the following is

(a) The boiling point of a liquid at one bar is called standard boiling point of the liquid.

(b) The vapour pressure of a liquid is constant at constant temperature.

(c) The SI unit of coefficient of viscosity of a liquid is pascal second.

(d) The boiling point of a liquid is the same at all external pressures.

Show Answer

Answer: (d)

Question 34. The van der Waals equation reduces itself to the ideal gas equation at:

(a) High pressure and low temperature

(b) Low pressure and low temperature

(c) low pressure and high temperature

(d) high pressure alone

Show Answer

Answer: (c)

Question 35. The maximum number of molecules is present in :

(a) $15\mathrm{L}$ of ${\mathrm{H}}_2$ gas at NTP

(b) $5\mathrm{L}$ of ${\mathrm{N}}_2$ gas at NTP

(c) $0.5\mathrm{g}$ of ${\mathrm{H}}_2$ gas

(d) $10\mathrm{g}$ of ${\mathrm{O}}_2$ gas

Show Answer

Answer: (a)

Question 36. A certain sample of a gas has a volume of 0.2 litre measured at $1\mathrm{atm}$ pressure and $0^{\circ }\mathrm{C}$. At the same pressure but ${273}^{\circ }\mathrm{C}$, its volume will be :

(a) $0.4\mathrm{L}$

(b) $0.8\mathrm{L}$

(c) $27.8\mathrm{L}$

(d) $55.6\mathrm{L}$

Show Answer

Answer: (a)

Question 37. A gas deviates from ideal behavior at a high pressure because its molecules:

(a) have kinetic energy

(b) are bound by covalent bonds

(c) attract one another

(d) show the Tyndall effect

Show Answer

Answer: (c)

Question 38. The pressure exerted by 1 mole of methane in a 0.25 litre container at $300\mathrm{K}$ using van der Waals equation (given $a=2.253\mathrm{atm}{\mathrm{L}}^2{\mathrm{mol}}^{-2},b=0.0428\mathrm{L}{\mathrm{mol}}^{-1}$ ) is

(a) $82.82\mathrm{atm}$

(b) $152.51\mathrm{atm}$

(c) $190.52\mathrm{atm}$

(d) $70.52\mathrm{atm}$

Show Answer

Answer: (a)

Question 39. To what temperature must a neon gas sample be heated to double its pressure, if the initial volume of a gas at ${75}^{\circ }\mathrm{C}$ is decreased by $15$ ?

(a) ${319}^{\circ }\mathrm{C}$

(b) ${592}^{\circ }\mathrm{C}$

(c) ${128}^{\circ }\mathrm{C}$

(d) ${60}^{\circ }\mathrm{C}$

Show Answer

Answer: (a)

Question 40. Which pair of the gases diffuses with the same rate at same temperature and pressure?

(a) $\mathrm{CO}$ and $\mathrm{NO}$

(b) ${\mathrm{NO}}_2$ and ${\mathrm{CO}}_2$

(c) ${\mathrm{NH}}_3$ and ${\mathrm{PH}}_3$

(d) $\mathrm{NO}$ and ${\mathrm{C}}_2{\mathrm{H}}_6$

Show Answer

Answer: (d)

Question 41. A gas has double the average velocity of ${\mathrm{SO}}_2$ gas at any temperature. The gas may be:

(a) ${\mathrm{CO}}_2$

(b) ${\mathrm{C}}_2{\mathrm{H}}_4$

(c) ${\mathrm{CH}}_4$

(d) ${\mathrm{O}}_2$

Show Answer

Answer: (c)

Question 42. The density of a gas is $1.964\mathrm{g}{\mathrm{dm}}^{-3}$ at $273\mathrm{K}$ and $76\mathrm{cm}\mathrm{Hg}$. The gas is:

(a) ${\mathrm{CH}}_4$

(b) ${\mathrm{C}}_2{\mathrm{H}}_6$

(c) ${\mathrm{CO}}_2$

(d) $\mathrm{Xe}$

Show Answer

Answer: (c)

Question 43. Non-ideal gases approach ideal behavior:

(a) high temperature and high pressure

(b) high temperature and low pressure

(c) low temperature and high pressure

(d) low temperature and low pressure

Show Answer

Answer: (b)

Question 44. According to kinetic theory of gases for a diatomic molecule:

(a) the pressure exerted by the gas is proportional to the mean square speed of the molecules

(b) the pressure exerted by the gas is proportional to the root mean square speed of the molecules

(c) the root mean square speed is inversely proportional to the temperature

(d) the mean translational K.E. of the molecule, is directly proportional to the square root of the absolute temperature

Show Answer

Answer: (a)

Question 45. The root mean square velocity of one mole of a monoatomic gas having molar mass $M$ is $u_{\mathrm{rms}}$. The relation between average kinetic energy $(E)$ of the gas and $u_{\mathrm{rms}}$ is :

(a) $u_{\text{rms }}=\sqrt{\frac{3E}{2M}}$

(b) $u_{\mathrm{rms}}=\sqrt{\frac{2E}{3M}}$

(c) $u_{\mathrm{rms}}=\sqrt{\frac{2E}{M}}$

(d) $u_{\mathrm{rms}}=\sqrt{\frac{E}{3M}}$

Show Answer

Answer: (c)

Question 46. The term that corrects for the attractive forces present in a real gas in the van der Waals equation is:

(a) $nb$

(b) $\frac{a{n}^2}{v^2}$

(c) $\frac{-a{n}^2}{V^2}$

(d) $-nb$

Show Answer

Answer: (b)

Question 47. What is the dominant intermolecular force or bond that must be overcome in converting liquid ${\mathrm{CH}}_3\mathrm{OH}$ to gas?

(a) Dipole-dipole interaction

(b) Covalent bonds

(c) London-dispersion force

(d) Hydrogen bonding

Show Answer

Answer: (d)

Question 48. Most probable speed, average speed and rms speed are related as:

(a) $1:1.224:1.128$

(b) $1.128:1:1.224$

(c) $1:1.128:1.224$

(d) $1.224:1.128:1$

Show Answer

Answer: (c)

Question 49. The rms speed of hydrogen molecules at room temperature is $2400\mathrm{m}{\mathrm{s}}^{-1}$. At room temperature the rms speed of oxygen molecules would be:

(a) $400\mathrm{m}{\mathrm{s}}^{-1}$

(b) $300\mathrm{m}{\mathrm{s}}^{-1}$

(c) $600\mathrm{m}{\mathrm{s}}^{-1}$

(d) $1600\mathrm{m}{\mathrm{s}}^{-1}$

Show Answer

Answer: (c)

Question 50. The critical temperature of a gas is that temperature:

(a) above which it can no longer remain in the gaseous state

(b) above which it cannot be liquefied by pressure

(c) at which itsolidifies

(d) at which the volume of the gas becomes zero

Show Answer

Answer: (b)

Question 51. Two samples of gases $A$ and $B$ are at the same temperature. The molecules of $A$ are travelling four times faster than the molecules of $B$. The ratio of their molar masses $M_A/M_B$ will be:

(a) 16

(b) 4

(c) $\frac{1}{4}$

(d) $\frac{1}{16}$

Show Answer

Answer: (d)

Question 52. The compressibility factor of one mole of a gas is defined as $Z=PV/RT$. The compressibility factor of an ideal gas is:

(a) zero

(b) 1

(c) -1

(d) infinity

Show Answer

Answer: (b)

Question 53. A mixture of three gases $X$ (density 1.0), $Y$ (density 0.2 ) and $Z$ (density 0.4 ) is enclosed in a vessel at constant temperature. When the equilibrium is established, the gas/gases:

(a) X will be at the top of the vessel

(b) Ywill be at the top of the vessel

(c) Z will be at the top of the vessel

(d) will mix homogeneously throughout the vessel

Show Answer

Answer: (d)

Question 54. When an ideal gas undergoes unrestricted expansion, no cooling occurs because the molecules:

(a) exert no attractive forces on each other

(b) do work equal to loss of kinetic energy

(c) collide without loss of energy

(d) are above the inversion temperature

Show Answer

Answer: (a)

Question 55. Which of the following mixture of gases at room temperature would not follow Dalton’s law of partial pressures?

(a) ${\mathrm{NO}}_2$ and ${\mathrm{O}}_2$

(b) ${\mathrm{NH}}_3$ and $\mathrm{HCl}$

(c) $\mathrm{CO}$ and ${\mathrm{CO}}_2$

(d) ${\mathrm{SO}}_2$ and ${\mathrm{O}}_2$

Show Answer

Answer: (b)

Question 56. The root mean square velocity of an ideal gas at constant pressure, varies with density ( $d$ ) as :

(a) $\frac{1}{\sqrt{d}}$

(b) $\sqrt{d}$

(c) $d$

(d) $d^2$

Show Answer

Answer: (a)

Question 57. Equal masses of methane and oxygen are mixed in an empty container at ${25}^{\circ }\mathrm{C}$. The fraction of the total pressure exerted by oxygen is:

(a) $\frac{1}{3}\times \frac{273}{298}$

(b) $\frac{1}{3}$

(c) $\frac{1}{2}$

(d) $\frac{2}{3}$

Show Answer

Answer: (b)

Question 58. When $r,P$ and $M$ represent rate of diffusion, pressure and molecular mass respectively, then the ratio of the rates of diffusion $\left(r_A/r_B\right)$ of two gases $A$ and $B$, is given as:

(a) ${\left(P_{\mathrm{A}}/P_{\mathrm{B}}\right)}^{1/2}\left(M_{\mathrm{B}}/M_{\mathrm{A}}\right)$

(b) $\left(P_{\mathrm{A}}/P_{\mathrm{B}}\right){\left(M_{\mathrm{A}}/M_{\mathrm{B}}\right)}^{1/2}$

(c) ${\left(P_{\mathrm{A}}/P_{\mathrm{B}}\right)}^{1/2}\left(M_{\mathrm{A}}/M_{\mathrm{B}}\right)$

(d) $\left(P_{\mathrm{A}}/P_{\mathrm{B}}\right){\left(M_{\mathrm{B}}/M_{\mathrm{A}}\right)}^{1/2}$

Show Answer

Answer: (d)

Question 59. The molecular velocity of any gas is:

(a) directly proportional to square of temperature

(b) directly proportional to square root of temperature

(c) inversely proportional to square root of temperature

(d) inversely proportional to absolute temperature

Show Answer

Answer: (b)

Question 60. Under critical state of a gas, for one mole of a gas, compressibility factor is :

(a) $\frac{3}{8}$

(b) 1

(c) $\frac{8}{3}$

(d) $\frac{1}{4}$

Show Answer

Answer: (a)

Question 61. A $100\mathrm{mL}$ flask contained ${\mathrm{H}}_2$, at 200 Torr and a $200\mathrm{mL}$ flask contained $\mathrm{He}$ at 100 Torr. The two flask were then connected so that each gas filled their combined volume. Assuming no change in temperature, total pressure is:

(a) 300 Torr

(b) 150 Torr

(c) 66.66 Torr

(d) 133.3 Torr

Show Answer

Answer: (d)

Question 62. The temperature at which ${\mathrm{N}}_2$ molecules would have the same average speed as that of helium atoms at $300\mathrm{K}$ is:

(a) $300\mathrm{K}$

(b) $1050\mathrm{K}$

(c) $2100\mathrm{K}$

(d) $14700\mathrm{K}$

Show Answer

Answer: (c)

Question 63. A large irregularly - shaped closed tank is first evacuated and then connected to a 50 litre cylinder containing compressed nitrogen gas. The gas pressure in the cylinder, originally at 21.0 atm, falls to $2.0\mathrm{atm}$, after it is connected to the evacuated tank. The volume of the tank is :

(a) 475 litres

(b) 50 litres

(c) 525 litres

(d) 21.45 litres

Show Answer

Answer: (a)