Current Electricity
Exercises
3.1 The storage battery of a car has an emf of $12 \mathrm{~V}$. If the internal resistance of the battery is $0.4 \Omega$, what is the maximum current that can be drawn from the battery?
Show Answer
Answer
Emf of the battery, $E=12 \mathrm{~V}$
Internal resistance of the battery, $r=0.4 \Omega$
Maximum current drawn from the battery $=I$
According to Ohm’s law,
$$ \begin{aligned} E & =I r \\ I & =\frac{E}{r} \\ & =\frac{12}{0.4}=30 \mathrm{~A} \end{aligned} $$
The maximum current drawn from the given battery is $30 \mathrm{~A}$.
3.2 A battery of emf $10 \mathrm{~V}$ and internal resistance $3 \Omega$ is connected to a resistor. If the current in the circuit is $0.5 \mathrm{~A}$, what is the resistance of the resistor? What is the terminal voltage of the battery when the circuit is closed?
Show Answer
Answer
Emf of the battery, $E=10 \mathrm{~V}$
Internal resistance of the battery, $r=3 \Omega$
Current in the circuit, $I=0.5 \mathrm{~A}$
Resistance of the resistor $=R$
The relation for current using Ohm’s law is,
$I=\frac{E}{R+r}$
$R+r=\frac{E}{I}$
$=\frac{10}{0.5}=20 \Omega$
$\therefore R=20-3=17 \Omega$
Terminal voltage of the resistor $=V$
According to Ohm’s law,
$V=I R$
$=0.5 \times 17$
$=8.5 \mathrm{~V}$
Therefore, the resistance of the resistor is $17 \Omega$ and the terminal voltage is
$8.5 \mathrm{~V}$.
3.3 At room temperature $\left(27.0{ }^{\circ} \mathrm{C}\right)$ the resistance of a heating element is $100 \Omega$. What is the temperature of the element if the resistance is found to be $117 \Omega$, given that the temperature coefficient of the material of the resistor is $1.70 \times 10^{-4}{ }^{\circ} \mathrm{C}^{-1}$.
Show Answer
Answer
Room temperature, $T=27^{\circ} \mathrm{C}$
Resistance of the heating element at $T, R=100 \Omega$
Let $T_{1}$ is the increased temperature of the filament.
Resistance of the heating element at $T_{1}, R_{1}=117 \Omega$
Temperature co-efficient of the material of the filament,
$\alpha=1.70 \times 10^{-4 \circ} \mathrm{C}^{-1}$
$\alpha$ is given by the relation,
$\alpha=\frac{R_{1}-R}{R\left(T_{1}-T\right)}$
$T_{1}-T=\frac{R_{1}-R}{R \alpha}$
$T_{1}-27=\frac{117-100}{100\left(1.7 \times 10^{-4}\right)}$
$T_{1}-27=1000$
$T_{1}=1027^{\circ} \mathrm{C}$
Therefore, at $1027^{\circ} \mathrm{C}$, the resistance of the element is $117 \Omega$.
3.4 A negligibly small current is passed through a wire of length $15 \mathrm{~m}$ and uniform cross-section $6.0 \times 10^{-7} \mathrm{~m}^{2}$, and its resistance is measured to be $5.0 \Omega$. What is the resistivity of the material at the temperature of the experiment?
Show Answer
Answer
Length of the wire, $l=15 \mathrm{~m}$
Area of cross-section of the wire, $a=6.0 \times 10^{-7} \mathrm{~m}^{2}$
Resistance of the material of the wire, $R=5.0 \Omega$
Resistivity of the material of the wire $=\rho$
Resistance is related with the resistivity as
$$ \begin{aligned} R & =\rho \frac{l}{A} \\ \rho & =\frac{R A}{l} \\ & =\frac{5 \times 6 \times 10^{-7}}{15}=2 \times 10^{-7} \Omega \mathrm{m} \end{aligned} $$
Therefore, the resistivity of the material is $2 \times 10^{-7} \Omega \mathrm{m}$.
3.5 A silver wire has a resistance of $2.1 \Omega$ at $27.5^{\circ} \mathrm{C}$, and a resistance of $2.7 \Omega$ at $100{ }^{\circ} \mathrm{C}$. Determine the temperature coefficient of resistivity of silver.
Show Answer
Answer
Temperature, $T_{1}=27.5^{\circ} \mathrm{C}$
Resistance of the silver wire at $T_{1}, R_{1}=2.1 \Omega$
Temperature, $T_{2}=100^{\circ} \mathrm{C}$
Resistance of the silver wire at $T_{2}, R_{2}=2.7 \Omega$
Temperature coefficient of silver $=\alpha$
It is related with temperature and resistance as
$$ \begin{aligned} \alpha & =\frac{R_{2}-R_{1}}{R_{1}\left(T_{2}-T_{1}\right)} \\ & =\frac{2.7-2.1}{2.1(100-27.5)}=0.0039^{\circ} \mathrm{C}^{-1} \end{aligned} $$
Therefore, the temperature coefficient of silver is $0.0039^{\circ} \mathrm{C}^{-1}$.
3.6 A heating element using nichrome connected to a $230 \mathrm{~V}$ supply draws an initial current of 3.2 A which settles after a few seconds to a steady value of $2.8 \mathrm{~A}$. What is the steady temperature of the heating element if the room temperature is $27.0 ^{\circ} \mathrm{C}$ ? Temperature coefficient of resistance of nichrome averaged over the temperature range involved is $1.70 \times 10 ^{-4}{ }^{\circ} \mathrm{C} ^{-1}$.
Show Answer
Answer
Supply voltage, $V=230 \mathrm{~V}$
Initial current drawn, $I_{1}=3.2 \mathrm{~A}$
Initial resistance $=R_{1}$, which is given by the relation,
$$ \begin{aligned} R_{1} & =\frac{V}{I} \\ & =\frac{230}{3.2}=71.87 \Omega \end{aligned} $$
Steady state value of the current, $I_{2}=2.8 \mathrm{~A}$
Resistance at the steady state $=R_{2}$, which is given as $R_{2}=\frac{230}{2.8}=82.14 \Omega$
Temperature co-efficient of nichrome, $\alpha=1.70 \times 10^{-4}{ }^{\circ} \mathrm{C}^{-1}$
Initial temperature of nichrome, $T_{1}=27.0^{\circ} \mathrm{C}$
Study state temperature reached by nichrome $=T_{2}$
$T_{2}$ can be obtained by the relation for $\alpha$,
$\alpha=\frac{R_{2}-R_{1}}{R_{1}\left(T_{2}-T_{1}\right)}$
$T_{2}-27^{\circ} \mathrm{C}=\frac{82.14-71.87}{71.87 \times 1.7 \times 10^{-4}}=840.5$
$T_{2}=840.5+27=867.5^{\circ} \mathrm{C}$
Therefore, the steady temperature of the heating element is $867.5^{\circ} \mathrm{C}$
3.7 Determine the current in each branch of the network shown in Fig. 3.20:
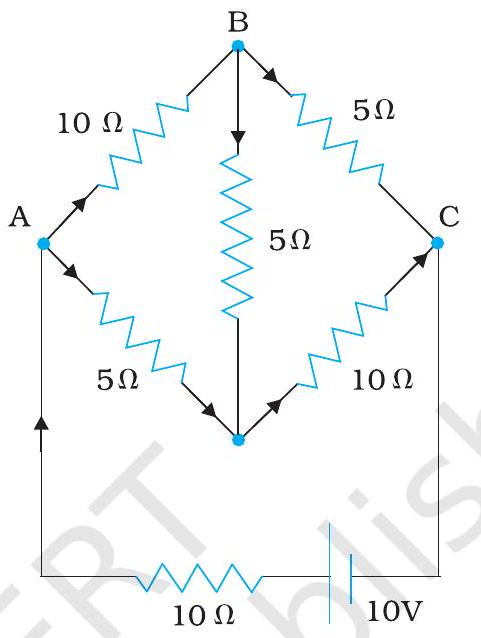
FIGURE 3.20
Show Answer
# Content Missing3.8 A storage battery of emf $8.0 \mathrm{~V}$ and internal resistance $0.5 \Omega$ is being charged by a $120 \mathrm{~V}$ dc supply using a series resistor of $15.5 \Omega$. What is the terminal voltage of the battery during charging? What is the purpose of having a series resistor in the charging circuit?
Show Answer
Answer
Emf of the storage battery, $E=8.0 \mathrm{~V}$
Internal resistance of the battery, $r=0.5 \Omega$
DC supply voltage, $V=120 \mathrm{~V}$
Resistance of the resistor, $R=15.5 \Omega$
Effective voltage in the circuit $=V^{1}$
$R$ is connected to the storage battery in series. Hence, it can be written as
$V^{1}=V-E$
$V^{1}=120-8=112 \mathrm{~V}$
Current flowing in the circuit $=I$, which is given by the relation,
$$ \begin{aligned} I & =\frac{V^{1}}{R+r} \\ & =\frac{112}{15.5+5}=\frac{112}{16}=7 \mathrm{~A} \end{aligned} $$
Voltage across resistor $R$ given by the product, $I R=7 \times 15.5=108.5 \mathrm{~V}$
DC supply voltage $=$ Terminal voltage of battery + Voltage drop across $R$
Terminal voltage of battery $=120-108.5=11.5 \mathrm{~V}$
A series resistor in a charging circuit limits the current drawn from the external source. The current will be extremely high in its absence. This is very dangerous.
3.9 The number density of free electrons in a copper conductor estimated in Example 3.1 is $8.5 \times 10^{28} \mathrm{~m}^{-3}$. How long does an electron take to drift from one end of a wire $3.0 \mathrm{~m}$ long to its other end? The area of cross-section of the wire is $2.0 \times 10^{-6} \mathrm{~m}^{2}$ and it is carrying a current of $3.0 \mathrm{~A}$.
Show Answer
Answer
Number density of free electrons in a copper conductor, $n=8.5 \times 10^{28} \mathrm{~m}^{-3}$ Length of the copper wire, $l=3.0 \mathrm{~m}$
Area of cross-section of the wire, $A=2.0 \times 10^{-6} \mathrm{~m}^{2}$
Current carried by the wire, $I=3.0 \mathrm{~A}$, which is given by the relation,
$I=n A \mathrm{e} V_{\mathrm{d}}$
Where,
$\mathrm{e}=$ Electric charge $=1.6 \times 10^{-19} \mathrm{C}$
$V_{\mathrm{d}}=$ Drift velocity $=\frac{\text { Length of the wire }(l)}{\text { Time taken to cover } l(t)}$
$I=n A \mathrm{e} \frac{l}{t}$
$t=\frac{n A \mathrm{e} l}{I}$
$=\frac{3 \times 8.5 \times 10^{28} \times 2 \times 10^{-6} \times 1.6 \times 10^{-19}}{3.0}$
$=2.7 \times 10^{4} \mathrm{~s}$
Therefore, the time taken by an electron to drift from one end of the wire to the other is $2.7 \times 10^{4} \mathrm{~s}$.










