Answer

There are two charges,

$q_{1}=5 \times 10^{-8} \mathrm{C}$

$q_{2}=-3 \times 10^{-8} \mathrm{C}$

Distance between the two charges, $d=16 \mathrm{~cm}=0.16 \mathrm{~m}$

Consider a point $\mathrm{P}$ on the line joining the two charges, as shown in the given figure.

$r=$ Distance of point $\mathrm{P}$ from charge $q_{1}$

Let the electric potential $(V)$ at point $\mathrm{P}$ be zero.

Potential at point $\mathrm{P}$ is the sum of potentials caused by charges $q_{1}$ and $q_{2}$ respectively.

$\therefore V=\frac{q_{1}}{4 \pi \in_{0} r}+\frac{q_{2}}{4 \pi \in_{0}(d-r)}$

Where,

$\in_{0}=$ Permittivity of free space

For $V=0$, equation (i) reduces to

$$ \begin{aligned} & \frac{q_{1}}{4 \pi \in_{0} r}=-\frac{q_{2}}{4 \pi \in_{0}(d-r)} \\ & \frac{q_{1}}{r}=\frac{-q_{2}}{d-r} \\ & \frac{5 \times 10^{-8}}{r}=-\frac{\left(-3 \times 10^{-8}\right)}{(0.16-r)} \\ & \frac{0.16}{r}-1=\frac{3}{5} \\ & \frac{0.16}{r}=\frac{8}{5} \\ & \therefore r=0.1 \mathrm{~m}=10 \mathrm{~cm} \end{aligned} $$

Therefore, the potential is zero at a distance of $10 \mathrm{~cm}$ from the positive charge between the charges.

Suppose point $\mathrm{P}$ is outside the system of two charges at a distance $s$ from the negative charge, where potential is zero, as shown in the following figure.

For this arrangement, potential is given by,

$$ \begin{equation*} V=\frac{q_{1}}{4 \pi \epsilon_{0} s}+\frac{q_{2}}{4 \pi \in_{0}(s-d)} \tag{ii} \end{equation*} $$

For $V=0$, equation (ii) reduces to

$$ \frac{q_{1}}{4 \pi \in_{0} s}=-\frac{q_{2}}{4 \pi \in_{0}(s-d)} $$

$\frac{q_{1}}{s}=\frac{-q_{2}}{s-d}$

$\frac{5 \times 10^{-8}}{s}=-\frac{\left(-3 \times 10^{-8}\right)}{(s-0.16)}$

$1-\frac{0.16}{s}=\frac{3}{5}$

$\frac{0.16}{s}=\frac{2}{5}$

$\therefore s=0.4 \mathrm{~m}=40 \mathrm{~cm}$

Therefore, the potential is zero at a distance of $40 \mathrm{~cm}$ from the positive charge outside the system of charges.

Answer

The given figure shows six equal amount of charges, $q$, at the vertices of a regular hexagon.

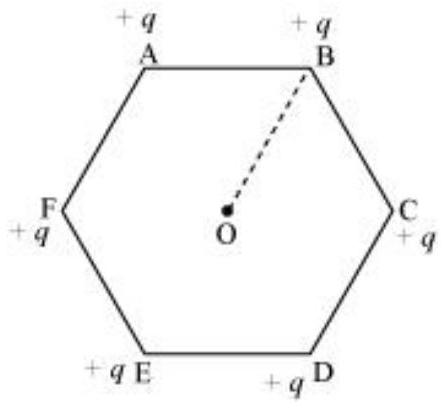
Where,

Charge, $q=5 \mu \mathrm{C}=5 \times 10^{-6} \mathrm{C}$

Side of the hexagon, $l=\mathrm{AB}=\mathrm{BC}=\mathrm{CD}=\mathrm{DE}=\mathrm{EF}=\mathrm{FA}=10 \mathrm{~cm}$

Distance of each vertex from centre $\mathrm{O}, d=10 \mathrm{~cm}$

Electric potential at point $\mathrm{O}$,

$$ V=\frac{6 \times q}{4 \pi \epsilon_{0} d} $$

Where,

$$ \in_{0}=\text { Permittivity of free space } $$

$$ \begin{aligned} & \frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} \mathrm{~N} \mathrm{C}^{-2} \mathrm{~m}^{-2} \\ & \therefore V=\frac{6 \times 9 \times 10^{9} \times 5 \times 10^{-6}}{0.1} \\ & \quad=2.7 \times 10^{6} \mathrm{~V} \end{aligned} $$

Therefore, the potential at the centre of the hexagon is $2.7 \times 10^{6} \mathrm{~V}$.

Answer

The situation is represented in the given figure.

An equipotential surface is the plane on which total potential is zero everywhere. This plane is normal to line $\mathrm{AB}$. The plane is located at the mid-point of line $\mathrm{AB}$ because the magnitude of charges is the same.

The direction of the electric field at every point on this surface is normal to the plane in the direction of $\mathrm{AB}$.

Answer

Radius of the spherical conductor, $r=12 \mathrm{~cm}=0.12 \mathrm{~m}$

Charge is uniformly distributed over the conductor, $q=1.6 \times 10^{-7} \mathrm{C}$

Electric field inside a spherical conductor is zero. This is because if there is field inside the conductor, then charges will move to neutralize it.

Electric field $E$ just outside the conductor is given by the relation,

$$ E=\frac{q}{4 \pi \epsilon_{0} r^{2}} $$

Where,

$$ \epsilon_{0}=\text { Permittivity of free space } $$

$\frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-2}$

$\therefore E=\frac{1.6 \times 10^{-7} \times 9 \times 10^{-9}}{(0.12)^{2}}$

$=10^{5} \mathrm{~N} \mathrm{C}^{-1}$

Therefore, the electric field just outside the sphere is $10^{5} \mathrm{~N} \mathrm{C}^{-1}$.

Electric field at a point $18 \mathrm{~m}$ from the centre of the sphere $=E_{1}$

Distance of the point from the centre, $d=18 \mathrm{~cm}=0.18 \mathrm{~m}$

$$ \begin{aligned} E_{1} & =\frac{q}{4 \pi \in_{0} d^{2}} \\ & =\frac{9 \times 10^{9} \times 1.6 \times 10^{-7}}{\left(18 \times 10^{-2}\right)^{2}} \\ & =4.4 \times 10^{4} \mathrm{~N} / \mathrm{C} \end{aligned} $$

Therefore, the electric field at a point $18 \mathrm{~cm}$ from the centre of the sphere is

$4.4 \times 10^{4} \mathrm{~N} / \mathrm{C}$

Capacitance between the parallel plates of the capacitor, $\mathrm{C}=8 \mathrm{pF}$

Initially, distance between the parallel plates was $d$ and it was filled with air. Dielectric constant of air, $k=1$

Capacitance, $C$, is given by the formula,

$$ \begin{align*} C & =\frac{k \in_{0} A}{d} \\ & =\frac{\in_{0} A}{d} \tag{i} \end{align*} $$

Where,

$A=$ Area of each plate

$$ \epsilon_{0}=\text { Permittivity of free space } $$

If distance between the plates is reduced to half, then new distance, $d=\frac{d}{2}$

Dielectric constant of the substance filled in between the plates, $k^{\prime}=6$

Hence, capacitance of the capacitor becomes

$$ \begin{equation*} C^{\prime}=\frac{k^{\prime} \in_{0} A}{d^{\prime}}=\frac{6 \in_{0} A}{\frac{d}{2}} \tag{ii} \end{equation*} $$

Taking ratios of equations (i) and (ii), we obtain

$$ \begin{aligned} C^{\prime} & =2 \times 6 C \\ & =12 C \\ & =12 \times 8=96 \mathrm{pF} \end{aligned} $$

Therefore, the capacitance between the plates is $96 \mathrm{pF}$.

Answer

Capacitance of each of the three capacitors, $C=9 \mathrm{pF}$

Equivalent capacitance $\left(C^{\prime}\right)$ of the combination of the capacitors is given by the relation,

$$ \begin{aligned} \frac{1}{C^{\prime}} & =\frac{1}{C}+\frac{1}{C}+\frac{1}{C} \\ & =\frac{1}{9}+\frac{1}{9}+\frac{1}{9}=\frac{3}{9}=\frac{1}{3} \end{aligned} $$

$\therefore C^{\prime}=3 \mu \mathrm{F}$

Therefore, total capacitance of the combination is $3 \mu \mathrm{F}$.

Supply voltage, $V=100 \mathrm{~V}$

Potential difference $\left(V^{\prime}\right)$ across each capacitor is equal to one-third of the supply voltage.

$$ \therefore V^{\prime}=\frac{V}{3}=\frac{120}{3}=40 \mathrm{~V} $$

Therefore, the potential difference across each capacitor is $40 \mathrm{~V}$.

Answer

Capacitances of the given capacitors are

$$ \begin{aligned} & C_{1}=2 \mathrm{pF} \\ & C_{2}=3 \mathrm{pF} \\ & C_{3}=4 \mathrm{pF} \end{aligned} $$

For the parallel combination of the capacitors, equivalent capacitor $C^{\prime}$ is given by the algebraic sum,

$$ C^{\prime}=2+3+4=9 \mathrm{pF} $$

Therefore, total capacitance of the combination is $9 \mathrm{pF}$.

Supply voltage, $V=100 \mathrm{~V}$

The voltage through all the three capacitors is same $=V=100 \mathrm{~V}$

Charge on a capacitor of capacitance $C$ and potential difference $V$ is given by the relation,

$q=V C \ldots$ (i)

For $\mathrm{C}=2 \mathrm{pF}$,

Charge $=V C=100 \times 2=200 \mathrm{pC}=2 \times 10^{-10} \mathrm{C}$

For $\mathrm{C}=3 \mathrm{pF}$,

Charge $=V C=100 \times 3=300 \mathrm{pC}=3 \times 10^{-10} \mathrm{C}$

For $\mathrm{C}=4 \mathrm{pF}$,

Charge $=V C=100 \times 4=200 \mathrm{pC}=4 \times 10^{-10} \mathrm{C}$

Answer

Area of each plate of the parallel plate capacitor, $A=6 \times 10^{-3} \mathrm{~m}^{2}$

Distance between the plates, $d=3 \mathrm{~mm}=3 \times 10^{-3} \mathrm{~m}$

Supply voltage, $V=100 \mathrm{~V}$

Capacitance $C$ of a parallel plate capacitor is given by,

$C=\frac{\in_{0} A}{d}$

Where,

$$ \epsilon_{0}=\text { Permittivity of free space } $$

$=8.854 \times 10^{-12} \mathrm{~N}^{-1} \mathrm{~m}^{-2} \mathrm{C}^{-2}$

$$ \begin{aligned} \therefore C & =\frac{8.854 \times 10^{-12} \times 6 \times 10^{-3}}{3 \times 10^{-3}} \\ & =17.71 \times 10^{-12} \mathrm{~F} \\ & =17.71 \mathrm{pF} \end{aligned} $$

Potential $V$ is related with the charge $q$ and capacitance $C$ as

$$ \begin{aligned} & V=\frac{q}{C} \\ & \therefore q=V C \\ & =100 \times 17.71 \times 10^{-12} \\ & =1.771 \times 10^{-9} \mathrm{C} \end{aligned} $$

Therefore, capacitance of the capacitor is $17.71 \mathrm{pF}$ and charge on each plate is $1.771 \times$ $10^{-9} \mathrm{C}$.

Answer

Dielectric constant of the mica sheet, $k=6$

Initial capacitance, $C=1.771 \times 10^{-11} \mathrm{~F}$

New capacitance, $C^{\prime}=k C=6 \times 1.771 \times 10^{-11}=106 \mathrm{pF}$

Supply voltage, $V=100 \mathrm{~V}$

New charge, $q^{\prime}=C^{\prime} V=6 \times 1.771 \times 10^{-9}=1.06 \times 10^{-8} \mathrm{C}$

Potential across the plates remains $100 \mathrm{~V}$.

Dielectric constant, $k=6$

Initial capacitance, $C=1.771 \times 10^{-11} \mathrm{~F}$

New capacitance, $C^{\prime}=k C=6 \times 1.771 \times 10^{-11}=106 \mathrm{pF}$

If supply voltage is removed, then there will be no effect on the amount of charge in the plates.

Charge $=1.771 \times 10^{-9} \mathrm{C}$

Potential across the plates is given by,

$$ \begin{aligned} \therefore V^{\prime} & =\frac{q}{C^{\prime}} \\ & =\frac{1.771 \times 10^{-9}}{106 \times 10^{-12}} \\ & =16.7 \mathrm{~V} \end{aligned} $$

Answer

Capacitor of the capacitance, $C=12 \mathrm{pF}=12 \times 10^{-12} \mathrm{~F}$

Potential difference, $V=50 \mathrm{~V}$

Electrostatic energy stored in the capacitor is given by the relation,

$$ \begin{aligned} E & =\frac{1}{2} C V^{2} \\ & =\frac{1}{2} \times 12 \times 10^{-12} \times(50)^{2} \\ & =1.5 \times 10^{-8} \mathrm{~J} \end{aligned} $$

Therefore, the electrostatic energy stored in the capacitor is $1.5 \times 10^{-8} \mathrm{~J}$.

Answer

Capacitance of the capacitor, $C=600 \mathrm{pF}$

Potential difference, $V=200 \mathrm{~V}$

Electrostatic energy stored in the capacitor is given by,

$$ \begin{aligned} E & =\frac{1}{2} C V^{2} \\ & =\frac{1}{2} \times\left(600 \times 10^{-12}\right) \times(200)^{2} \\ & =1.2 \times 10^{-5} \mathrm{~J} \end{aligned} $$

If supply is disconnected from the capacitor and another capacitor of capacitance $C=600$ $\mathrm{pF}$ is connected to it, then equivalent capacitance $(C)$ of the combination is given by,

$$ \begin{aligned} & \frac{1}{C^{\prime}}=\frac{1}{C}+\frac{1}{C} \\ & \quad=\frac{1}{600}+\frac{1}{600}=\frac{2}{600}=\frac{1}{300} \\ & \therefore C^{\prime}=300 \mathrm{pF} \end{aligned} $$

New electrostatic energy can be calculated as

$$ \begin{aligned} E^{\prime} & =\frac{1}{2} \times C^{\prime} \times V^{2} \\ & =\frac{1}{2} \times 300 \times(200)^{2} \\ & =0.6 \times 10^{-5} \mathrm{~J} \end{aligned} $$

Loss in electrostatic energy $=E-E^{\prime}$

$$ \begin{aligned} & =1.2 \times 10^{-5}-0.6 \times 10^{-5} \\ & =0.6 \times 10^{-5} \\ & =6 \times 10^{-6} \mathrm{~J} \end{aligned} $$

Therefore, the electrostatic energy lost in the process is $6 \times 10^{-6} \mathrm{~J}$.