Redox Reactions
Exercise
8.1 Assign oxidation number to the underlined elements in each of the following species:
(a) $\mathrm{NaH_2} \mathrm{PO_4}$
(b) $\mathrm{NaHSO_4}$
(c) $\mathrm{H_4} \mathrm{P_2} \mathrm{O_7}$
(d) $\mathrm{K_2} \mathrm{MnO_4}$
(e) $\mathrm{CaO_2}$
(f) $\mathrm{NaBH_4}$
(g) $\mathrm{H_2} \underline {\mathrm{S}_2} \mathrm{O_7}$
(h) $\mathrm{KAl}\left(\mathrm{SO_4}\right)_{2} \cdot 12 \mathrm{H_2} \mathrm{O}$
Show Answer
Answer
(a) $NaH_2 \underline PO_4$
Let the oxidation number of $P$ be $x$.
We know that,
Oxidation number of $Na=+1$
Oxidation number of $H=+1$
Oxidation number of $O=-2$
$\Rightarrow \stackrel{+1}{Na} \stackrel{+1}{H} \stackrel{x}{P} \stackrel{-2}{O_4}$
Then, we have
$1(+1)+2(+1)+1(x)+4(-2)=0$
$\Rightarrow 1+2+x-8=0$
$\Rightarrow x=+5$
Hence, the oxidation number of $P$ is +5 .
(b) $NaHSO_4$
$\stackrel{+1}{Na} \stackrel{+1}{H} \stackrel{x}{S} O_4$
Then, we have
$l(+1)+l(+1)+l(x)+4(-2)=0$
$\Rightarrow 1+1+x-8=0$
$\Rightarrow x=+6$
Hence, the oxidation number of $S$ is +6 .
(c) $H_4 \underline P_2 O_7$ $\stackrel{+1}{H_4} \stackrel{x}{P} \stackrel{-2}O_7$
Then, we have
$4(+1)+2(x)+7(-2)=0$
$\Rightarrow 4+2 x-14=0$
$\Rightarrow 2 x=+10$
$\Rightarrow x=+5$
Hence, the oxidation number of $P$ is +5 .
(d) $K_2 \underline {MnO_4}$
$ \stackrel{+1}{K_2} \stackrel{x}{Mn} \stackrel{-2}{O_4} $
Then, we have
$2(+1)+x+4(-2)=0$
$\Rightarrow 2+x-8=0$
$\Rightarrow x=+6$
Hence, the oxidation number of $Mn$ is +6 .
(e) $CaO \underline O_2$
$\stackrel{+2}{Ca} \stackrel{x_O^{2}}{ }$
Then, we have
$(+2)+2(x)=0$
$\Rightarrow 2+2 x=0$
$\Rightarrow x=-1$
Hence, the oxidation number of $O$ is - 1 .
(f) $NaBH_4$
$\stackrel{+1}{Na} \stackrel{x}B^{-1} H_4$
Then, we have
$1(+1)+1(x)+4(-1)=0$
$\Rightarrow 1+x-4=0$
$\Rightarrow x=+3$
Hence, the oxidation number of $B$ is +3 .
(g) $H_2 \underline S_2 O_7$ $\stackrel{+1}{H_2} S_2 \stackrel{-2}{O}$
Then, we have
$2(+1)+2(x)+7(-2)=0$
$\Rightarrow 2+2 x-14=0$
$\Rightarrow 2 x=12$
$\Rightarrow x=+6$
Hence, the oxidation number of $S$ is +6 .
(h) $KAl(\underline SO_4)_2 \cdot 12 H_2 O$
$\stackrel{+1}{KAl}(\stackrel{x^{2}-SO_4}{ })_2 .12 \stackrel{+1}{H_2} \stackrel{-2}{O}$
Then, we have
$1(+1)+1(+3)+2(x)+8(-2)+24(+1)+12(-2)=0$
$\Rightarrow 1+3+2 x-16+24-24=0$
$\Rightarrow 2 x=12$
$\Rightarrow x=+6$
Or,
We can ignore the water molecule as it is a neutral molecule. Then, the sum of the oxidation numbers of all atoms of the water molecule may be taken as zero. Therefore, after ignoring the water molecule, we have
$1(+1)+1(+3)+2(x)+8(-2)=0$
$\Rightarrow 1+3+2 x-16=0$
$\Rightarrow 2 x=12$
$\Rightarrow x=+6$
Hence, the oxidation number of $S$ is +6 .
8.2 What are the oxidation number of the underlined elements in each of the following and how do you rationalise your results?
(a) $\mathrm{KI_3}$
(b) $\mathrm{H_2} \underline {\mathrm{S}_4} \mathrm{O_6}$
(c) $\mathrm{Fe_3} \mathrm{O_4}$
(d) $\mathrm{CH_3} \mathrm{CH_2} \mathrm{OH}$
(e) $\mathrm{CH_3} \mathrm{COOH}$
Show Answer
Answer
(a) $KI_3$
In $KI_3$, the oxidation number (O.N.) of $K$ is +1 . Hence, the average oxidation number of $I$ is $-\frac{1}{3}$. However, O.N. cannot be fractional. Therefore, we will have to consider the structure of $KI_3$ to find the oxidation states.
In a $KI_3$ molecule, an atom of iodine forms a coordinate covalent bond with an iodine molecule.
$ \stackrel{+1}{K^+}[\stackrel{0}{I-}\stackrel{0}{I} \longleftarrow \stackrel{-1}{I} ]^{-} $
Hence, in a $KI_3$ molecule, the O.N. of the two I atoms forming the $I_2$ molecule is 0 , whereas the O.N. of the I atom forming the coordinate bond is -1.
(b) $H_2 \underline S_4 O_6$
$ \stackrel{+1}{H_2} \stackrel{\stackrel{x}{S} O_4 \stackrel{-2}{O}}{6} $
Now, $2(+1)+4(x)+6(-2)=0$
$\Rightarrow 2+4 x-12=0$
$\Rightarrow 4 x=10$
$\Rightarrow x=+2 \frac{1}{2}$
However, O.N. cannot be fractional. Hence, S must be present in different oxidation states in the molecule.
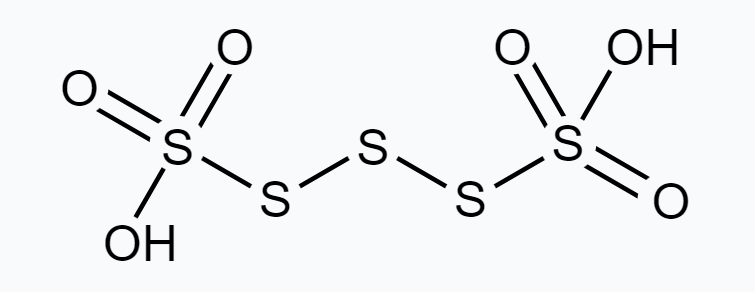
The O.N. of two of the four $S$ atoms is +5 and the O.N. of the other two $S$ atoms is 0.
(c) $\underline Fe_3 O_4$
On taking the O.N. of O as -2, the O.N. of Fe is found to be ${ }^{+2 \frac{2}{3}}$. However, O.N. cannot be fractional. Here, one of the three Fe atoms exhibits the O.N. of +2 and the other two Fe atoms exhibit the O.N. of +3 .
$\stackrel{+2}{FeO}, \stackrel{+3}{F} e_2 O_3$
(d) $CH_3 \underline CH_2 OH$
$2(x)+6(+1)+1(-2)=0$
or, $2 x+4=0$
or, $x=-2$
Hence, the O.N. of C is -2.
(e)
$CH_3 \underline {COOH}$
$2(x)+4(+1)+2(-2)=0$
or, $2 x=0$
or, $x=0$
However, 0 is average O.N. of C. The two carbon atoms present in this molecule are present in different environments. Hence, they cannot have the same oxidation number. Thus, $C$ exhibits the oxidation states of +2 and âe"2 in $CH_3 COOH$.
8.3 Justify that the following reactions are redox reactions:
(a) $\mathrm{CuO}$ (s) $+\mathrm{H_2}$ (g) $\rightarrow \mathrm{Cu}$ (s) $+\mathrm{H_2} \mathrm{O}$ (g)
(b) $\mathrm{Fe_2} \mathrm{O_3}$ (s) $+3 \mathrm{CO}$ (g) $\rightarrow 2 \mathrm{Fe}(\mathrm{s})+3 \mathrm{CO_2}$ (g)
(c) $4 \mathrm{BCl_3}(\mathrm{~g})+3 \mathrm{LiAlH_4}(\mathrm{~s}) \rightarrow 2 \mathrm{~B_2} \mathrm{H_6}(\mathrm{~g})+3 \mathrm{LiCl}(\mathrm{s})+3 \mathrm{AlCl_3}$ (s)
(d) $2 \mathrm{~K}(\mathrm{~s})+\mathrm{F_2}(\mathrm{~g}) \rightarrow 2 \mathrm{~K}^{+} \mathrm{F}^{-}(\mathrm{s})$
(e) $4 \mathrm{NH_3}(\mathrm{~g})+5 \mathrm{O_2}(\mathrm{~g}) \rightarrow 4 \mathrm{NO}(\mathrm{g})+6 \mathrm{H_2} \mathrm{O}(\mathrm{g})$
Show Answer
Answer
(a)
$ CuO _{(s)}+H _{2(g)} \longrightarrow Cu _{(s)}+H_2 O _{(g)} $
Let us write the oxidation number of each element involved in the given reaction as:
$\stackrel{+2}{Cu} \stackrel{-2}{O}(s)+\stackrel{0}{H}(g) \longrightarrow \stackrel{0}{C} u _{(s)}+\stackrel{+1}H_2 \stackrel{-2}O _{(g)}$
Here, the oxidation number of $Cu$ decreases from +2 in $CuO$ to 0 in $Cu$ i.e., $CuO$ is reduced to $Cu$. Also, the oxidation number of $H$ increases from 0 in $H_2$ to +1 in $H_2 O$ i.e., $H_2$ is oxidized to $H_2 O$. Hence, this reaction is a redox reaction.
(b)
$ Fe_2 O _{3(s)}+3 CO _{(g)} \longrightarrow 2 Fe _{(s)}+3 CO _{2(g)} $
Let us write the oxidation number of each element in the given reaction as:
$ \stackrel{+3}{Fe_2} \stackrel{-2}{O_3} + \stackrel{+2 -2}{3CO_{(g)}} \longrightarrow 2\stackrel{0}{Fe_{(s)}} + 3\stackrel{+4-2}{CO_{2(g)}} $
Here, the oxidation number of $Fe$ decreases from +3 in $Fe_2 O_3$ to 0 in $Fe$ i.e., $Fe_2 O_3$ is reduced to $Fe$. On the other hand, the oxidation number of $C$ increases from +2 in $CO$ to +4 in $CO_2$ i.e., $CO$ is oxidized to $CO_2$. Hence, the given reaction is a redox reaction.
(c)
$ 4 BCl _{3(g)}+3 LiAlH _{4(s)} \longrightarrow 2 B_2 H _{6(g)}+3 LiCl _{(s)}+3 AlCl _{3(s)} $
The oxidation number of each element in the given reaction can be represented as:
$ 4 \stackrel{+3}{B} \stackrel{-1}{Cl_{3(g)}} + \stackrel{+1+3-1}{\quad 3LiAlH_{4(s)}} \longrightarrow \stackrel{-3 \quad +1}{\quad 2B_2 H_{6(g)}} + \stackrel{+1-1}{3LiCl_{(s)}} + \stackrel{+3 -1}{\quad 3AlCl_{3(s)}} $
In this reaction, the oxidation number of $B$ decreases from +3 in $BCl_3$ to â “ $^{3}$ in $B_2 H_6$. i.e., $BCl_3$ is reduced to $B_2 H_6$. Also, the oxidation number of $H$ increases from â " 1 in $LiAlH_4$ to +1 in $B_2 H_6$ i.e., $LiAlH_4$ is oxidized to $B_2 H_6$. Hence, the given reaction is a redox reaction.
(d) $2 K _{(s)}+F _{2(g)} \longrightarrow 2 K^{+} F^{-} _{(s)}$
The oxidation number of each element in the given reaction can be represented as:
$2 \stackrel{0}K _{(s)}+\stackrel{0}F _{2(g)}^{\longrightarrow} 2 \stackrel{+1}K^{+} \stackrel{-1}F _{(s)}^{-}$
In this reaction, the oxidation number of $K$ increases from 0 in $K$ to +1 in $KF$ i.e., $K$ is oxidized to $KF$. On the other hand, the oxidation number of $F$ decreases from 0 in $F_2$ to - 1 in $K F$ i.e., $F_2$ is reduced to KF.
Hence, the above reaction is a redox reaction.
(e)
$ 4NH_{3(g)} + 5O_{2(g)} \longrightarrow 4NO_{(g)} + 6H_2O_{(g)} $
The oxidation number of each element in the given reaction can be represented as:
$4 \stackrel{-3}N _{3(g)}+5 \stackrel{0}O _{2(g)}^{\longrightarrow} 4 \stackrel{+2}{N} \stackrel{-2}O _{(g)}+6 \stackrel{+1}H_2 \stackrel{-2}O _{(g)}$
Here, the oxidation number of $N$ increases from - 3 in $NH_3$ to +2 in $NO$. On the other hand, the oxidation number of $O_2$ decreases from 0 in $O_2$ to - 2 in $NO$ and $H_2 O$ i.e., $O_2$ is reduced. Hence, the given reaction is a redox reaction.
8.4 Fluorine reacts with ice and results in the change:
$\mathrm{H_2} \mathrm{O}(\mathrm{s})+\mathrm{F_2}(\mathrm{~g}) \rightarrow \mathrm{HF}(\mathrm{g})+\mathrm{HOF}(\mathrm{g})$
Justify that this reaction is a redox reaction.
Show Answer
Answer
Let us write the oxidation number of each atom involved in the given reaction above its symbol as:
$ \stackrel{+1 -2}{H_2O} + \stackrel{0}{F} \longrightarrow \stackrel{+1-1}{HF} + \stackrel{+1-2+1}{HOF} $
Here, we have observed that the oxidation number of $F$ increases from 0 in $F_2$ to +1 in $HOF$. Also, the oxidation number decreases from 0 in $F_2$ to -1 in HF. Thus, in the above reaction, $F$ is both oxidized and reduced. Hence, the given reaction is a redox reaction.
8.5 Calculate the oxidation number of sulphur, chromium and nitrogen in $\mathrm{H_2} \mathrm{SO_5}, \mathrm{Cr_2} \mathrm{O_7}^{2-}$ and $\mathrm{NO_3}^{-}$. Suggest structure of these compounds. Count for the fallacy.
Show Answer
Answer
(i)
$\stackrel{+1}{H_2} \stackrel{x}{S^{-2}} S_5$
$2(+1)+1(x)+5(-2)=0$
$\Rightarrow 2+x-10=0$
$\Rightarrow x=+8$
However,the O.N. of $S$ cannot be +8. $S$ has six valence electrons. Therefore, the O.N. of $S$ cannot be more than +6 . The structure of $H_2 SO_5$ is shown as follows:
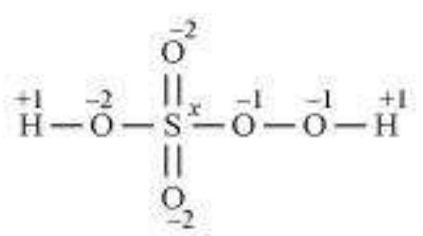
Now, $2(+1)+1(x)+3(-2)+2(-1)=0$
$\Rightarrow 2+x-6-2=0$
$\Rightarrow x=+6$
Therefore, the O.N. of $S$ is +6 .
(ii)
${ }^{Cr} r_2 O_7^{2-}$
$2(x)+7(-2)=-2$
$\Rightarrow 2 x-14=-2$
$\Rightarrow x=+6$
Here, there is no fallacy about the O.N. of $Cr$ in $Cr_2 O_7^{2-}$.
The structure of $Cr_2 O_7^{2-}$ is shown as follows:
Here, each of the two $Cr$ atoms exhibits the O.N. of +6 .
(iii) $\stackrel{x}{N} \stackrel{2-}{O_3^{-}}$
$1(x)+3(-2)=-1$
$\Rightarrow x-6=-1$
$\Rightarrow x=+5$
Here, there is no fallacy about the O.N. of $N$ in $NO_3^{-}$.
The structure of $NO_3^{-}$is shown as follows:
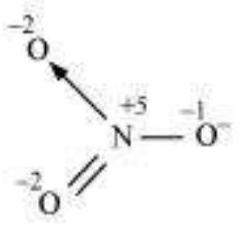
TheN atom exhibits the O.N. of +5 .
8.6 Write formulas for the following compounds:
(a) Mercury(II) chloride
(b) Nickel(II) sulphate
(c) Tin(IV) oxide
(d) Thallium(I) sulphate
(e) Iron(III) sulphate
(f) Chromium(III) oxide
Show Answer
Answer
(a) Mercury (II) chloride:
$HgCl_2$
(b) Nickel (II) sulphate:
$NiSO_4$
(c) Tin (IV) oxide:
$SnO_2$
(d) Thallium (I) sulphate:
$TI_2 SO_4$
(e) Iron (III) sulphate:
$Fe_2(SO_4)_3$
(f) Chromium (III) oxide:
$Cr_2 O_3$
8.7 Suggest a list of the substances where carbon can exhibit oxidation states from -4 to +4 and nitrogen from -3 to +5 .
Show Answer
Answer
The substances where carbon can exhibit oxidation states from - 4 to +4 are listed in the following table.
| Substance | O.N. of carbon |
|---|---|
| $CH_2 Cl_2$ | 0 |
| $ClC \equiv CCl$ | +1 |
| $HCA \equiv CH$ | $- 1$ |
| $CHCl_3, CO$ | +2 |
| $CH_3 Cl$ | $- 2$ |
| $Cl_3 C - CCl_3$ | +3 |
| $H_3 C - CH_3$ | -3 |
| $CCl_4- CO_2$ | +4 |
| $CH_4$ | -4 |
The substances where nitrogen can exhibit oxidation states from -3 to +5 are listed in the following table.
| Substance | O.N. of nitrogen |
|---|---|
| $N_2$ | 0 |
| $N_2 O$ | +1 |
| $N_2 H_2$ | $- 1$ |
| $NO$ | +2 |
| $N_2 H_4$ | $-2$ |
| $N_2 O_3$ | +3 |
| $NH_3$ | $- 3$ |
| $NO_2$ | +4 |
| $N_2 O_5$ | +5 |
8.8 While sulphur dioxide and hydrogen peroxide can act as oxidising as well as reducing agents in their reactions, ozone and nitric acid act only as oxidants. Why ?
Show Answer
Answer
In sulphur dioxide $(SO_2)$, the oxidation number (O.N.) of $S$ is +4 and the range of the O.N. that $S$ can have is from +6 to -2 .
Therefore, $SO_2$ can act as an oxidising as well as a reducing agent.
In hydrogen peroxide $(H_2 O_2)$, the O.N. of $O$ is -1 and the range of the O.N. that $O$ can have is from 0 to -2 . $O$ can sometimes also attain the oxidation numbers +1 and +2 . Hence, $H_2 O_2$ can act as an oxidising as well as a reducing agent.
In ozone $(O_3)$, the $O . N$. of $O$ is zero and the range of the O.N. that $O$ can have is from $O$ to -2. Therefore, the O.N. of $O$ can only decrease in this case. Hence, $O_3$ acts only as an oxidant.
In nitric acid $(HNO_3)$, the O.N. of $N$ is +5 and the range of the O.N. that $N$ can have is from +5 to -3 . Therefore, the O.N. of $N$ can only decrease in this case. Hence, $HNO_3$ acts only as an oxidant.
8.9 Consider the reactions:
(a) $6 \mathrm{CO_2}(\mathrm{~g})+6 \mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{C_6} \mathrm{H_12} \mathrm{O_6}(\mathrm{aq})+6 \mathrm{O_2}(\mathrm{~g})$
(b) $\mathrm{O_3}(\mathrm{~g})+\mathrm{H_2} \mathrm{O_2}(\mathrm{l}) \rightarrow \mathrm{H_2} \mathrm{O}(\mathrm{l})+2 \mathrm{O_2}(\mathrm{~g})$
Why it is more appropriate to write these reactions as :
(a) $6 \mathrm{CO_2}(\mathrm{~g})+12 \mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{C_6} \mathrm{H_12} \mathrm{O_6}(\mathrm{aq})+6 \mathrm{H_2} \mathrm{O}(\mathrm{l})+6 \mathrm{O_2}(\mathrm{~g})$
(b) $\mathrm{O_3}$ (g) $+\mathrm{H_2} \mathrm{O_2}$ (l) $\rightarrow \mathrm{H_2} \mathrm{O}(\mathrm{l})+\mathrm{O_2}(\mathrm{~g})+\mathrm{O_2}$ (g)
Also suggest a technique to investigate the path of the above (a) and (b) redox reactions.
Show Answer
Answer
(a)The process of photosynthesis involves two steps.
Step 1:
$H_2 O$ decomposes to give $H_2$ and $O_2$.
$ 2 H_2 O _{(l)} \longrightarrow 2 H _{2(g)}+O _{2(g)} $
Step 2:
The $H_2$ produced in step 1reduces $CO_2$, thereby producing glucose $(C_6 H _{12} O_6)$ and $H_2 O$.
$ 6 CO _{2(g)}+12 H _{2(g)} \longrightarrow C_6 H _{12} O _{6(s)}+6 H_2 O _{(l)} $
Now, the net reaction of the process is given as:
$ \begin{aligned} 2 H_2 O _{(i)} & .\longrightarrow 2 H _{2(g)}+O _{2(g)}] \times 6 \\ 6 CO _{2(g)}+12 H _{2(g)} & \longrightarrow C_6 H _{12} O _{6(g)}+6 H_2 O _{(l)} \\ 6 CO _{2(g)}+12 H_2 O _{(l)} & \longrightarrow C_6 H _{12} O _{6(g)}+6 H_2 O _{(l)}+6 O _{2(g)} \end{aligned} $
Itis more appropriate to write the reaction as given above because water molecules are also produced in the process of photosynthesis.
The path of this reaction can be investigated by using radioactive $H_2 O^{18}$ in place of $H_2 O$.
(b) $O_2$ is produced from each of the two reactants $O_3$ and $H_2 O_2$. For this reason, $O_2$ is written twice.
The given reaction involves two steps. First, $O_3$ decomposes to form $O_2$ and $O$. In the second step, $H_2 O_2$ reacts with the O produced in the first step, thereby producing $H_2 O$ and $O_2$.
$ \begin{aligned} & O _{3(g)} \longrightarrow O _{2(g)}+O _{(g)} \\ & H_2 O _{2(l)}+O _{(g)} \longrightarrow H_2 O _{(l)}+O _{2(g)} \\ & H_2 O _{2(l)}+O _{3(g)} \longrightarrow H_2 O _{(l)}+O _{2(g)}+O _{2(g)} \end{aligned} $
The path of this reaction can be investigated by using $H_2 O_2{ }^{18}$ or $O_3^{18}$.
8.10 The compound $\mathrm{AgF_2}$ is unstable compound. However, if formed, the compound acts as a very strong oxidising agent. Why?
Show Answer
Answer
The oxidation state of $Ag$ in $AgF_2$ is +2 . But, +2 is an unstable oxidation state of $Ag$. Therefore, whenever $AgF_2$ is formed, silver readily accepts an electron to form $Ag^{+}$. This helps to bring the oxidation state of $Ag$ down from +2 to a more stable state of +1 . As a result, $AgF_2$ acts as a very strong oxidizing agent.
8.11 Whenever a reaction between an oxidising agent and a reducing agent is carried out, a compound of lower oxidation state is formed if the reducing agent is in excess and a compound of higher oxidation state is formed if the oxidising agent is in excess. Justify this statement giving three illustrations.
Show Answer
Answer
Whenever a reaction between an oxidising agent and a reducing agent is carried out, a compound of lower oxidation state is formed if the reducing agent is in excess and a compound of higher oxidation state is formed if the oxidising agent is in excess. This can be illustrated as follows:
(i) $P_4$ and $F_2$ are reducing and oxidising agents respectively.
If an excess of $P_4$ is treated with $F_2$, then $PF_3$ will be produced, wherein the oxidation number (O.N.) of $P$ is +3 .
$ P_4 \text{ (excess) }+F_2 \longrightarrow \stackrel{+3}{P_3} $
However, if $P_4$ is treated with an excess of $F_2$, then $PF_5$ will be produced, wherein the O.N. of $P$ is +5 . $P_4+F_2$ (excess) $\longrightarrow \stackrel{+5}{P_5}$
(ii) $K$ acts as a reducing agent, whereas $O_2$ is an oxidising agent.
If an excess of $K$ reacts with $O_2$, then $K_2 O$ will be formed, wherein the $O . N$. of $O$ is $\hat{a} \in e^{\text{" }} 2$.
$ 4 K \text{ (excess) }+O_2 \longrightarrow 2 K_2{ }^{-2} $
However, if $K$ reacts with an excess of $O_2$, then $K_2 O_2$ will be formed, wherein the $O . N$. of $O$ is $\hat{a} E^{\text{" }} 1$.
$ 2 K+O_2 \text{ (excess) } \longrightarrow K_2{\stackrel{-1}{O_2}}^{-1} $
(iii)C is a reducing agent, while $O_2$ acts as an oxidising agent.
If an excess of $C$ is burnt in the presence of insufficient amount of $O_2$, then $CO$ will be produced, wherein the $O . N$. of $C$ is +2 .
$ C(\text{ excess })+O_2 \longrightarrow \stackrel{+2}{C} O $
On the other hand, if $C$ is burnt in an excess of $O_2$, then $CO_2$ will be produced, wherein the $O . N$. of $C$ is +4 .
$ C+O_2 \text{ (excess) } \longrightarrow \stackrel{+4}{CO_2} $
8.12 How do you count for the following observations?
(a) Though alkaline potassium permanganate and acidic potassium permanganate both are used as oxidants, yet in the manufacture of benzoic acid from toluene we use alcoholic potassium permanganate as an oxidant. Why ? Write a balanced redox equation for the reaction.
(b) When concentrated sulphuric acid is added to an inorganic mixture containing chloride, we get colourless pungent smelling gas $\mathrm{HCl}$, but if the mixture contains bromide then we get red vapour of bromine. Why?
Show Answer
Answer
(a) In the manufacture of benzoic acid from toluene, alcoholic potassium permanganate is used as an oxidant because of the following reasons.
(i) In a neutral medium, $OH^{-}$ ions are produced in the reaction itself. As a result, the cost of adding an acid or a base can be reduced.
(ii) $KMnO_4$ and alcohol are homogeneous to each other since both are polar. Toluene and alcohol are also homogeneous to each other because both are organic compounds. Reactions can proceed at a faster rate in a homogeneous medium than in a heterogeneous medium. Hence, in alcohol, $KMnO_4$ and toluene can react at a faster rate.
The balanced redox equation for the reaction in a neutral medium is give as below:

(b) When conc. $H_2 SO_4$ is added to an inorganic mixture containing bromide, initially $HBr$ is produced. $HBr$, being a strong reducing agent reduces $H_2 SO_4$ to $SO_2$ with the evolution of red vapour of bromine.
$ \begin{aligned} & 2 NaBr+2 H_2 SO_4 \longrightarrow 2 NaHSO_4+2 HBr \\ & 2 HBr+H_2 SO_4 \longrightarrow Br_2+SO_2+2 H_2 O \\ & \text{ (red vapour) } \end{aligned} $
But, when conc. $H_2 SO_4$ is added to an inorganic mixture containing chloride, a pungent smelling gas $(HCl)$ is evolved. $HCl$, being a weak reducing agent, cannot reduce $H_2 SO_4$ to $SO_2$
$2 NaCl+2 H_2 SO_4 \longrightarrow 2 NaHSO_4+2 HCl$
8.13 Identify the substance oxidised reduced, oxidising agent and reducing agent for each of the following reactions:
(a) $2 \mathrm{AgBr}$ (s) $+\mathrm{C_6} \mathrm{H_6} \mathrm{O_2}$ (aq) $2 \mathrm{Ag}(\mathrm{s})+2 \mathrm{HBr}$ (aq) $+\mathrm{C_6} \mathrm{H_4} \mathrm{O_2}$ (aq)
(b) $\mathrm{HCHO}(\mathrm{l})+2 \left[\mathrm{Ag} \left(\mathrm{NH_3} \right)_{2} \right]^{+}(\mathrm{aq})+3 \mathrm{OH}^{-}(\mathrm{aq}) + 2 \mathrm{Ag}(\mathrm{s})+\mathrm{HCOO}^{-}(\mathrm{aq})+4 \mathrm{NH_3}(\mathrm{aq})+ 2 \mathrm{H2O}\mathrm{(l)}$
(c) $\mathrm{HCHO} \mathrm{(l)}+2 \mathrm{Cu}^{2+}(\mathrm{aq})+5 \mathrm{OH}^{-}(\mathrm{aq}) \quad \mathrm{Cu} 2 \mathrm{O}(\mathrm{s})+\mathrm{HCOO}^{-}(\mathrm{aq})+3 \mathrm{H_2} \mathrm{O}(\mathrm{l})$
(d) $\mathrm{N_2} \mathrm{H_4}(\mathrm{l})+2 \mathrm{H_2} \mathrm{O_2}(\mathrm{l}) \rightarrow \mathrm{N_2}(\mathrm{~g})+4 \mathrm{H_2} \mathrm{O}(\mathrm{l})$
(e) $\mathrm{Pb}(\mathrm{s})+\mathrm{PbO_2}(\mathrm{~s})+2 \mathrm{H_2} \mathrm{SO_4}(\mathrm{aq}) \rightarrow 2 \mathrm{PbSO_4}(\mathrm{~s})+2 \mathrm{H_2} \mathrm{O}(\mathrm{l})$
Show Answer
Answer
(a) Oxidised substance $ \longrightarrow C_6H_6O_2 $
Reduced substance $ \longrightarrow $ AgBr
Oxidising agent $ \longrightarrow A g B r$
Reducing agent $ \longrightarrow $ $C_6 H_6 O_2$
(b)Oxidised substance $\longrightarrow $ HCHO
Reduced substance $ \longrightarrow ,[Ag(NH_3)_2]^{+}$
Oxidising agent $ \longrightarrow ,[Ag(NH_3)_2]^{+}$
Reducing agent $ \longrightarrow $ HCHO
(c) Oxidised substance $ \longrightarrow $ HCHO
Reduced substance $ \longrightarrow Cu^{2+}$
Oxidising agent $ \longrightarrow $ $Cu^{2+}$
Reducing agent $ \longrightarrow $ $HCHO$
(d) Oxidised substance $ \longrightarrow N_2 H_4$
Reduced substance $ \longrightarrow $ $H_2 O_2$
Oxidising agent $ \longrightarrow H_2 O_2$
Reducing agent $\longrightarrow N_2H_4 $
(e) Oxidised substance $ \longrightarrow $ Pb
Reduced substance $ \longrightarrow PbO_2$
Oxidising agent $ \longrightarrow $ $PbO_2$
Reducing agent $\longrightarrow Pb $
8.14 Consider the reactions :
$2 \mathrm{~S_2} \mathrm{O_3}^{2-}(\mathrm{aq})+\mathrm{I_2}(\mathrm{~s}) \rightarrow \mathrm{S_4} \mathrm{O_6}^{2-}(\mathrm{aq})+2 \mathrm{I}^{-}(\mathrm{aq})$
$\mathrm{S_2} \mathrm{O_3}^{2-}(\mathrm{aq})+2 \mathrm{Br_2}(\mathrm{l})+5 \mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightarrow 2 \mathrm{SO_4}^{2-(\mathrm{aq})}+4 \mathrm{Br}^{-}(\mathrm{aq})+10 \mathrm{H}^{+}(\mathrm{aq})$
Why does the same reductant, thiosulphate react differently with iodine and bromine?
Show Answer
Answer
The average oxidation number (O.N.) of $S$ in $S_2 O_3^{2-}$ is +2. Being a stronger oxidising agent than $I_2$, $Br_2$ oxidises $S _2 O^{2-} _3 {\text{to }} SO_4^{2-}$, in which the O.N. of $S$ is +6 . However, $I_2$ is a weak oxidising agent. Therefore, it oxidises $S_2 O_3^{2-}$ to $S_4 O_6^{2-}$, in which the average O.N. of $S$ is only +2.5. As a result, $S_2 O_3^{2-}$ reacts differently with iodine and bromine.
8.15 Justify giving reactions that among halogens, fluorine is the best oxidant and among hydrohalic compounds, hydroiodic acid is the best reductant.
Show Answer
Answer
$F_2$ can oxidize $Cl^{-}$ to $Cl_2$, $Br^{-}$ to $Br_2$, and $l^{-} e^{e}$ to $I_2$ as:
$ \begin{aligned} & F _{2(a q)}+2 Cl _{(s)}^{-} \longrightarrow 2 F _{(a q)}^{-}+Cl _{(g)} \\ & F _{2(a q)}+2 Br _{(a q)}^{-} \longrightarrow 2 F _{(a q)}^{-}+Br _{2(l)} \\ & F _{2(a q)}+2 I _{(a q)}^{-} \longrightarrow 2 F _{(a q)}^{-}+I _{2(s)} \end{aligned} $
On the other hand, $Cl_2, Br_2$, and $I_2$ cannot oxidize $F^{-}$ to $F_2$. The oxidizing power of halogens increases in the order of $I_2<Br_2<Cl_2<F_2$. Hence, fluorine is the best oxidant among halogens.
$HI$ and $HBr$ can reduce $H_2 SO_4$ to $SO_2$, but $HCl$ and $HF$ cannot. Therefore, $HI$ and $HBr$ are stronger reductants than $HCl$ and $HF$.
$2 HI+H_2 SO_4 \longrightarrow I_2+SO_2+2 H_2 O$
$2 HBr+H_2 SO_4 \longrightarrow Br_2+SO_2+2 H_2 O$
Again, l- can reduce $Cu^{2+}$ to $Cu^{+}$, but $Br^{-}$ cannot.
$4 I _{(a q)}^{-}+2 Cu _{(a q)}^{2+} \longrightarrow Cu_2 I _{2(s)}+I _{2(a q)}$
Hence, hydroiodic acid is the best reductant among hydrohalic compounds.
Thus, the reducing power of hydrohalic acids increases in the order of $HF<HCl<HBr<HI$.
8.16 Why does the following reaction occur?
$\mathrm{XeO_6}{ }^{4-}(\mathrm{aq})+2 \mathrm{~F}^{-}(\mathrm{aq})+6 \mathrm{H}^{+}(\mathrm{aq}) \rightarrow \mathrm{XeO_3}(\mathrm{~g})+\mathrm{F_2}(\mathrm{~g})+3 \mathrm{H_2} \mathrm{O}(\mathrm{l})$
What conclusion about the compound $\mathrm{Na_4} \mathrm{XeO_6}$ (of which $\mathrm{XeO_6}^{4-}$ is a part) can be drawn from the reaction.
Show Answer
Answer
The given reaction occurs because $XeO_6^{4-}$ oxidises $F^{-}$and $F^{-}$reduces $XeO_6^{4-}$.
$\mathrm{XeO} _{6(\mathrm{aq})}^{4-}+2 \mathrm{~F}^{-1}{ } _{(\mathrm{aq})}+6 \mathrm{H} _{(\mathrm{aq})}^{+} \rightarrow \mathrm{XeO} _{3(\mathrm{~g})}^{+6}+\mathrm{F} _{2(\mathrm{~g})}^0+3 \mathrm{H} _2 \mathrm{O} _{(\mathrm{l})}$
In this reaction, the oxidation number (O.N.) of Xe decreases from +8 in $XeO_6^{4-}$ to +6 in $XeO_3$ and the O.N. of $F$ increases from - 1 in $F^{a \hat{e}}$ " to $O$ in $F_2$.
Hence, we can conclude that $Na_4 XeO_6$ is a stronger oxidising agent than $F^{a \epsilon}$
8.17 Consider the reactions:
(a) $\mathrm{H_3} \mathrm{PO_2}(\mathrm{aq})+4 \mathrm{AgNO_3}(\mathrm{aq})+2 \mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{H_3} \mathrm{PO_4}(\mathrm{aq})+4 \mathrm{Ag}(\mathrm{s})+4 \mathrm{HNO_3}(\mathrm{aq})$
(b) $\mathrm{H_3} \mathrm{PO_2}$ (aq) $+2 \mathrm{CuSO_4}(\mathrm{aq})+2 \mathrm{H_2} \mathrm{O}$ (l) $\rightarrow \mathrm{H_3} \mathrm{PO_4}$ (aq) $+2 \mathrm{Cu}$ (s) $+\mathrm{H_2} \mathrm{SO_4}(\mathrm{aq})$
(c) $\mathrm{C_6} \mathrm{H_5} \mathrm{CHO}(\mathrm{l})+2\left[\mathrm{Ag}\left(\mathrm{NH_3}\right)_{2}\right]^{+}(\mathrm{aq})+3 \mathrm{OH}^{-}(\mathrm{aq}) \rightarrow \mathrm{C_6} \mathrm{H_5} \mathrm{COO}^{-}(\mathrm{aq})+2 \mathrm{Ag}(\mathrm{s})+ 4 \mathrm{NH_3}(\mathrm{aq})+2 \mathrm{H_2} \mathrm{O}(\mathrm{l})$
(d) $\mathrm{C_6} \mathrm{H_5} \mathrm{CHO}(\mathrm{l})+2 \mathrm{Cu}^{2+}(\mathrm{aq})+5 \mathrm{OH}^{-}(\mathrm{aq}) \rightarrow$ No change observed.
What inference do you draw about the behaviour of $\mathrm{Ag}^{+}$and $\mathrm{Cu}^{2+}$ from these reactions?
Show Answer
Answer
$Ag^{+}$and $Cu^{2+}$ act as oxidising agents in reactions (a) and (b) respectively.
In reaction (c), $Ag^{+}$oxidises $C_6 H_5 CHO$ to $C_6 H_5 COO$, but in reaction (d), $Cu^{2+}$ cannot oxidise $C_6 H_5 CHO$.
Hence, we can say that $Ag^{+}$is a stronger oxidising agent than $Cu^{2+}$.
8.18 Balance the following redox reactions by ion - electron method :
(a) $\mathrm{MnO_4}^{-}$(aq) $+\mathrm{I}^{-}$(aq) $\rightarrow \mathrm{MnO_2}$ (s) $+\mathrm{I_2}$ (s) (in basic medium)
(b) $\mathrm{MnO_4}^{-}(\mathrm{aq})+\mathrm{SO_2}$ (g) $\rightarrow \mathrm{Mn}^{2+}(\mathrm{aq})+\mathrm{HSO_4}^{-}$(aq) (in acidic solution)
(c) $\mathrm{H_2} \mathrm{O_2}(\mathrm{aq})+\mathrm{Fe}^{2+}(\mathrm{aq}) \rightarrow \mathrm{Fe}^{3+}(\mathrm{aq})+\mathrm{H_2} \mathrm{O}$ (l) (in acidic solution)
(d) $\mathrm{Cr_2} \mathrm{O_7}^{2-}+\mathrm{SO_2}(\mathrm{~g}) \rightarrow \mathrm{Cr}^{3+}(\mathrm{aq})+\mathrm{SO_4}{ }^{2-}$ (aq) (in acidic solution)
Show Answer
Answer
(a) Step 1: The two half reactions involved in the given reaction are:
Oxidation half reaction: $\stackrel{-1}{I}(aq) \longrightarrow 0^{0}$
Reduction half reaction:
$ \stackrel{+7}{MnO} H _{4(a q)}^{-} \longrightarrow \stackrel{+4}{M} nO _{2(a q)} $
Step 2:
Balancing I in the oxidation half reaction, we have:
$ 2 I _{(a q)}^{-} \longrightarrow I _{2(s)} $
Now, to balance the charge, we add $2 e^{-}$ to the RHS of the reaction.
$ 2 I _{(a q)}^{-} \longrightarrow I _{2(s)}+2 e^{-} $
Step 3:
In the reduction half reaction, the oxidation state of $Mn$ has reduced from +7 to +4 . Thus, 3 electrons are added to the LHS of the reaction.
$ MnO _{4(a q)}^{-}+3 e^{-} \longrightarrow MnO _{2(a q)} $
Now, to balance the charge, we add $4 OH^{a+i}$ ions to the RHS of the reaction as the reaction is taking place in a basic medium.
$ MnO _{4(a q)}^{-}+3 e^{-} \longrightarrow MnO _{2(a q)}+4 OH^{-} $
Step 4:
In this equation, there are $6 O$ atoms on the RHS and $4 O$ atoms on the LHS. Therefore, two water molecules are added to the LHS.
$ MnO _{4(a q)}^{-}+2 H_2 O+3 e^{-} \longrightarrow MnO _{2(a q)}+4 OH^{-} $
Step 5:
Equalising the number of electrons by multiplying the oxidation half reaction by 3 and the reduction half reaction by 2 , we have:
$6 I _{(a q)}^{-} \longrightarrow 3 I _{2(s)}+6 e^{-}$
$2 MnO _{4(a q)}^{-}+4 H_2 O+6 e^{-} \longrightarrow 2 MnO _{2(s)}+8 OH _{(a q)}^{-}$
Step 6:
Adding the two half reactions, we have the net balanced redox reaction as:
$ 6 I _{(a q)}^{-}+2 MnO _{4(a q)}^{-}+4 H_2 O _{(l)} \longrightarrow 3 I _{2(s)}+2 MnO _{2(s)}+8 OH _{(a q)}^{-} $
(b)Following the steps as in part (a), we have the oxidation half reaction as:
$ SO _{2(g)}+2 H_2 O _{(j)} \longrightarrow HSO _{4(a q)}^{-}+3 H _{(a q)}^{+}+2 e _{(a q)}^{-} $
And the reduction half reaction as:
$ MnO _{4(a q)}^{-}+8 H _{(a q)}^{+}+5 e^{-} \longrightarrow Mn _{(a q)}^{2+}+4 H_2 O _{(l)} $
Multiplying the oxidation half reaction by 5 and the reduction half reaction by 2 , and then by adding them, we have the net balanced redox reaction as:
$ 2 MnO _{4(a q)}^{-}+5 SO _{2(g)}+2 H_2 O _{(i)}+H _{(a q)}^{+} \longrightarrow 2 Mn _{(a q)}^{2+}+5 HSO _{4(a q)}^{-} $
(c) Following the steps as in part (a), we have the oxidation half reaction as:
$ Fe _{(a q)}^{2+} \longrightarrow Fe^{3+} _{(a q)}+e^{-} $
And the reduction half reaction as:
$ H_2 O _{2(a q)}+2 H _{(a q)}^{+}+2 e^{-} \longrightarrow 2 H_2 O _{(l)} $
Multiplying the oxidation half reaction by 2 and then adding it to the reduction half reaction, we have the net balanced redox reaction as:
$ H_2 O _{2(a q)}+2 Fe^{2+} _{(a q)}+2 H _{(a q)}^{+} \longrightarrow 2 Fe^{3+} _{(a q)}+2 H_2 O _{(l)} $
(d) Following the steps as in part (a), we have the oxidation half reaction as:
$ SO _{2(g)}+2 H_2 O _{(i)} \longrightarrow SO _{4(a q)}^{2-}+4 H _{(a q)}^{+}+2 e^{-} $
And the reduction half reaction as:
$ Cr_2 O _{7(a q)}^{2-}+14 H _{(a q)}^{+}+6 e^{-} \longrightarrow 2 Cr^{3+} _{(a q)}+7 H_2 O _{(l)} $
Multiplying the oxidation half reaction by 3 and then adding it to the reduction half reaction, we have the net balanced redox reaction as:
$ Cr_2 O _{7(a q)}^{2-}+3 SO _{2(g)}+2 H _{(a q)}^{+} \longrightarrow 2 Cr _{(a q)}^{3+}+3 SO _{4(a q)}^{2-}+H_2 O _{(l)} $
8.19 Balance the following equations in basic medium by ion-electron method and oxidation number methods and identify the oxidising agent and the reducing agent.
(a) $\mathrm{P_4}(\mathrm{~s})+\mathrm{OH}^{-}(\mathrm{aq}) \rightarrow \mathrm{PH_3}(\mathrm{~g})+\mathrm{HPO_2}^{-}(\mathrm{aq})$
(b) $\mathrm{N_2} \mathrm{H_4}(\mathrm{l})+\mathrm{ClO_3}^{-}(\mathrm{aq}) \rightarrow \mathrm{NO}(\mathrm{g})+\mathrm{Cl}^{-}(\mathrm{g})$
(c) $\mathrm{Cl_2} \mathrm{O_7}$ (g) $+\mathrm{H_2} \mathrm{O_2}$ (aq) $\rightarrow \mathrm{ClO_2}^{-}$(aq) $+\mathrm{O_2}$ (g) $+\mathrm{H}^{+}$
Show Answer
Answer
(a)
The O.N. (oxidation number) of $P$ decreases from 0 in $P_4$ to -3 in $PH_3$ and increases from 0 in $P_4$ to +2 in $HPO_2^{-}$. Hence, $P_4$ acts both as an oxidizing agent and a reducing agent in this reaction.
lon-electron method:
The oxidation half equation is:
$P _{4(s)} \to H_2 PO_2{ }^{-}(aq)$
The $P$ atom is balanced as:
$\stackrel{0}P _{4(s)} \to 4 H_2 \stackrel{+1}{P} O_2^{-}(aq)$
The O.N. is balanced by adding 4 electrons as:
$P _{4(s)} \to 4 H_2 PO_2{ }^{-} _{(a q)}+4 e^{-}$
The charge is balanced by adding $8 OH^{-}$ as:
$ P_{4(s)} +8OH^-_{(aq)} \to 4 H_2 PO _{2(aq)} + 4e^-$
The $O$ and $H$ atoms are already balanced.
The reduction half equation is:
$P _{4(s)} \longrightarrow PH _{3(g)}$
The $P$ atom is balanced as
$\stackrel{0}{P _{4(s)}} \longrightarrow 4 \stackrel{-3}{P^{H _{3(g)}}}$
The O.N. is balanced by adding 12 electrons as:
$ P _{4(s)}+12 e^{-} \longrightarrow 4 PH _{3(g)} $
The charge is balanced by adding $12 OH^{-}$ as:
$ P_{4(s)}+12 e^- \longrightarrow 4 PH_{3(g)}+12 OH_{(a q)} $
The $O$ and $H$ atoms are balanced by adding $12 H_2 O$ as:
$ P_{4_(s)} + 12H_2O_{(i)} + 12e^- \longrightarrow 4PH_{3_{(g)}}+ 12HO^1_{aq} $
By multiplying equation (i) with 3 and (ii) with 2 and then adding them, the balanced chemical equation can be obtained as:
$P _{4(s)}+3 OH^{-} _{(a q)}+3 H_2 O \to PH_3+3 H_2 PO_2{ }^{-} _{(a q)}$
(b)

The oxidation number of $N$ increases from $- 2$ in $N_2 H_4$ to +2 in $NO$ and the oxidation number of $Cl$ decreases from
+5 in $ClO_3^{-}$to - 1 in $Cl^{\hat{\epsilon} \epsilon^{e}}$. Hence, in this reaction, $N_2 H_4$ is the reducing agent and $ClO_3^{-}$is the oxidizing agent.
lone electron method:
The oxidation half equation is:
$ \stackrel{-2}N_2 H _{4(l)} \longrightarrow \stackrel{+2}{N} O _{(g)} $
The $N$ atoms are balanced as:
$N_2 H _{4(l)} \longrightarrow 2 NO _{(g)}$
The oxidation number is balanced by adding 8 electrons as:
$N_2 H _{4(l)} \longrightarrow 2 NO _{(g)}+8 e^{-}$
The charge is balanced by adding $8 OH^{\circledR \epsilon}$ ions as:
$N_2 H _{4(l)}+8 OH _{(a q)}^{-} \longrightarrow 2 NO _{(g)}+8 e^{-}$
The $O$ atoms are balanced by adding $6 H_2 O$ as:
$ N_2H_4(i) +8OH^{-}_{aq} \longrightarrow 2NO(g) + 6H_2O(i) + 8e^{-} $
The reduction half equation is:
The oxidation number is balanced by adding 6 electrons as:
$ClO _{3(a q)}^{-}+6 e^{-} \longrightarrow Cl _{(a q)}^{-}$
The charge is balanced by adding $6 OH^{-}$ ions as:
$ ClO _{3(a q)}^{-}+6 e^{-} \longrightarrow Cl _{(a q)}^{-}+6 OH _{(a q)}^{-} $
The $O$ atoms are balanced by adding $3 H_2 O$ as:
$ ClO^-_3aq + 3H_2O_i + 6e^- \longrightarrow Cl^-_aq + 6OH^-_aq $
The balanced equation can be obtained by multiplying equation (i) with 3 and equation (ii) with 4 and then adding them as:
$ 3 N_2 H _{4(l)}+4 ClO _{3(a g)}^{-} \longrightarrow 6 NO _{(g)}+4 Cl _{(a q)}^{-}+6 H_2 O _{(l)} $
Oxidation number method:
Total decrease in oxidation number of $N=2 \times 4=8$
Total increase in oxidation number of $Cl=1 \times 6=6$
On multiplying $N_2 H_4$ with 3 and $ClO_3^{-}$with 4 to balance the increase and decrease in O.N., we get:
$ 3 N_2 H _{4(f)}+4 ClO _{3(a q)}^{-} \longrightarrow NO _{(g)}^{-}+Cl _{(a q)}^{-} $
The $N$ and $Cl$ atoms are balanced as:
$ 3 N_2 H _{4(l)}+4 ClO _{3(a q)}^{-} \longrightarrow 6 NO _{(g)}+4 Cl _{(a q)}^{-} $
The $O$ atoms are balanced by adding $6 H_2 O$ as:
$ 3 N_2 H _{4(l)}+4 ClO _{3(a q)}^{-} \longrightarrow 6 NO _{(g)}+4 Cl _{(a q)}^{-}+6 H_2 O _{(l)} $
This is the required balanced equation.
(c)
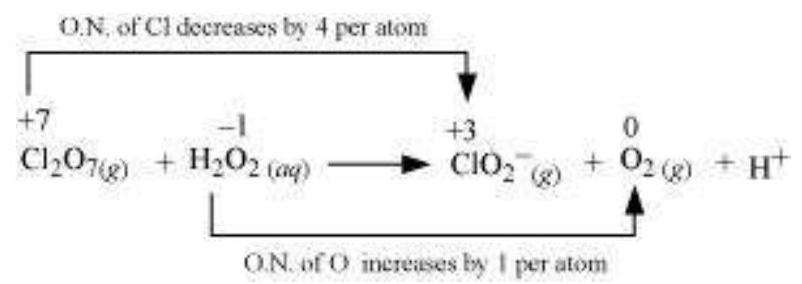
The oxidation number of $Cl$ decreases from +7 in $Cl_2 O_7$ to +3 in $ClO_2^{-}$and the oxidation number of $O$ increases from - 1 in $H_2 O_2$ to zero in $O_2$. Hence, in this reaction, $Cl_2 O_7$ is the oxidizing agent and $H_2 O_2$ is the reducing agent.
Ion-electron method:
The oxidation half equation is:
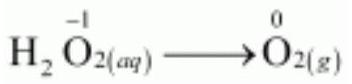
The oxidation number is balanced by adding 2 electrons as:
$ H_2 O _{2(a q)} \longrightarrow O _{2(g)}+2 e^{-} $
The charge is balanced by adding $2 OH^{a \epsilon}$ ions as:
$ H_2 O _{2(a q)}+2 OH _{(a q)}^{-} \longrightarrow O _{2(g)}+2 e^{-} $
The oxygen atoms are balanced by adding $2 H_2 O$ as:
$$ \begin{equation*} H_2O_{2(a q)}+2 OH_{(a q)}^{-} \longrightarrow O_{2(g)}+2 H_2 O _{(J)}+2 e^{-} \tag{i} \end{equation*} $$
The reduction half equation is:
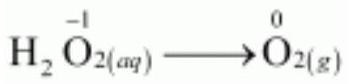
The $Cl$ atoms are balanced as:
$ Cl_2 O_{7(g)} \longrightarrow 2 ClO_{2(a q)}^{-} $
The oxidation number is balanced by adding 8 electrons as:
$ Cl_2O_{7(g)}+8 e^{-} \longrightarrow 2 ClO_{2(a q)}^{-} $
The charge is balanced by adding $6 OH^{-}$ as:
$ Cl_2 O _{7(g)}+8 e^{-} \longrightarrow 2 ClO _{2(a q)}^{-}+6 OH _{(a q)}^{-} $
The oxygen atoms are balanced by adding $3 H_2 O$ as:
$$ \begin{equation*} Cl_2 O _{7(g)}+3 H_2 O _{(l)} 8 e^{-} \longrightarrow 2 ClO _{2(a q)}^{-}+6 OH _{(a q)}^{-} \tag{ii} \end{equation*} $$
The balanced equation can be obtained by multiplying equation (i) with 4 and adding equation (ii) to it
as: $Cl_2 O _{7(g)}+4 H_2 O _{2(a q)}+2 OH _{(a q)}^{-} \longrightarrow 2 ClO _{2(a q)}^{-}+4 O _{2(g)}+5 H_2 O _{(l)}$
Oxidation number method:
Total decrease in oxidation number of $Cl_2 O_7=4 \times 2=8$
Total increase in oxidation number of $H_2 O_2=2 \times 1=2$
By multiplying $H_2 O_2$ and $O_2$ with 4 to balance the increase and decrease in the oxidation number, we get:
$ Cl_2 O _{7(g)}+4 H_2 O _{2(a q)} \longrightarrow ClO _{2(a q)}^{-}+4 O _{2(g)} $
The $Cl$ atoms are balanced as:
$ Cl_2 O _{7(g)}+4 H_2 O _{2(a q)} \longrightarrow 2 ClO _{2(a q)}^{-}+4 O _{2(g)} $
The $O$ atoms are balanced by adding $3 H_2 O$ as:
$ Cl_2 O _{7(g)}+4 H_2 O _{2(a q)} \longrightarrow 2 ClO _{2(a q)}^{-}+4 O _{2(g)}+3 H_2 O _{(\delta)} $
The $H$ atoms are balanced by adding $2 OH^{-}$ and $2 H_2 O$ as:
$ Cl_2 O _{7(g)}+4 H_2 O _{2(a q)}+2 OH _{(a q)}^{-} \longrightarrow 2 ClO _{2(a q)}^{-}+4 O _{2(g)}+5 H_2 O _{(l)} $
This is the required balanced equation.
8.20 What sorts of informations can you draw from the following reaction?
$\left(\mathrm{CN_2}(\mathrm{~g})+2 \mathrm{OH}^{-}(\mathrm{aq}) \rightarrow \mathrm{CN}^{-}(\mathrm{aq})+\mathrm{CNO}^{-}(\mathrm{aq})+\mathrm{H_2} \mathrm{O}(\mathrm{l})\right.$
Show Answer
Answer
The oxidation numbers of carbon in $(CN)^{2}, CN^{-}$ and $CNO^{\hat{A}}{ }^{-1}$ are $+3,+2$ and +4 respectively. These are obtained as shown below:
Let the oxidation number of $C$ be $x$.
$(CN)_2$
$2(x$-3 $)=0$
$\therefore x=3$
$CN^{-}$
$x$ - $3= - 1$
$\therefore x=2$
$CNO^{-}$
$x - 2$ = -1
$\therefore x=4$
The oxidation number of carbon in the various species is:
$ (\stackrel{+3}{C} N) _{2(g)}+2 OH _{(a q)}^{-} \longrightarrow \stackrel{+2}{C} N _{(a q)}^{-}+\stackrel{+4}{C} NO _{(a q)}^{-}+H_2 O _{(l)} $
It can be easily observed that the same compound is being reduced and oxidised simultaneously in the given equation. Reactions in which the same compound is reduced and oxidised is known as disproportionation reactions. Thus, it can be said that the alkaline decomposition of cyanogen is an example of disproportionation reaction.
8.21 The $\mathrm{Mn}^{3+}$ ion is unstable in solution and undergoes disproportionation to give $\mathrm{Mn}^{2+}$, $\mathrm{MnO_2}$, and $\mathrm{H}^{+}$ion. Write a balanced ionic equation for the reaction.
Show Answer
Answer
The given reaction can be represented as:
$ Mn _{(a q)}^{3+} \longrightarrow Mn _{(a q)}^{2+}+MnO _{2(s)}+H _{(a q)}^{+} $
The oxidation half equation is:

$ \stackrel{+3}{\quad Mn^{3+}} _{(aq)} \longrightarrow \stackrel{+4}{\quad \quad MnO _{2(s)}}$
The oxidation number is balanced by adding one electron as:
$ Mn _{(a q)}^{3+} \longrightarrow MnO _{2(s)}+e^{-} $
The charge is balanced by adding $4 H^{+}$ions as:
$ Mn _{(a q)}^{3+} \longrightarrow MnO _{2(s)}+4 H _{(a q)}^{+}+e^{-} $
The $O$ atoms and $H^{+}$ions are balanced by adding $2 H_2 O$ molecules as:
$$ \begin{equation*} Mn _{(a q)}^{3+}+2 H_2 O _{(f)} \longrightarrow MnO _{2(s)}+4 H _{(a q)}^{+}+e^{-} \tag{i} \end{equation*} $$
The reduction half equation is:
$ Mn _{(a q)}^{3+} \longrightarrow Mn _{(a q)}^{2+} $
The oxidation number is balanced by adding one electron as:
$$ \begin{equation*} Mn _{(a q)}^{3+}+e^{-} \longrightarrow Mn _{(a q)}^{2+} \tag{ii} \end{equation*} $$
The balanced chemical equation can be obtained by adding equation (i) and (ii) as:
$ 2 Mn _{(a q)}^{3+}+2 H_2 O _{(l)} \longrightarrow MnO _{2(s)}+2 Mn _{(a q)}^{2+}+4 H _{(a q)}^{+} $
8.22 Consider the elements : $\mathrm{Cs}, \mathrm{Ne}, \mathrm{I}$ and $\mathrm{F}$
(a) Identify the element that exhibits only negative oxidation state.
(b) Identify the element that exhibits only postive oxidation state.
(c) Identify the element that exhibits both positive and negative oxidation states.
(d) Identify the element which exhibits neither the negative nor does the positive oxidation state.
Show Answer
Answer
(a) F exhibits only negative oxidation state of -1 . (b) Cs exhibits positive oxidation state of +1 .
(c) I exhibits both positive and negative oxidation states. It exhibits oxidation states of $-1,+1,+3,+5$, and +7 .
(d) The oxidation state of $Ne$ is zero. It exhibits neither negative nor positive oxidation states.
8.23 Chlorine is used to purify drinking water. Excess of chlorine is harmful. The excess of chlorine is removed by treating with sulphur dioxide. Present a balanced equation for this redox change taking place in water.
Show Answer
Answer
The given redox reaction can be represented as:
$ Cl _{2(s)}+SO _{2(a q)}+H_2 O _{(l)} \longrightarrow Cl _{(a q)}^{-}+SO _{4(a q)}^{2-} $
The oxidation half reaction is:
$ \stackrel{+4}{S O _{2(a q)}} \longrightarrow \stackrel{+6}{S O^{2-} _{4(a q)} }$
The oxidation number is balanced by adding two electrons as:
$ SO _{2(a q)} \longrightarrow SO_4^{2-}(a q)+2 e^{-} $
The charge is balanced by adding $4 H^{+}$ions as:
$ SO _{2(a q)} \longrightarrow SO _{4(a q)}^{2-}+4 H _{(a q)}^{+}+2 e^{-} $
The $O$ atoms and $H^{+}$ions are balanced by adding $2 H_2 O$ molecules as:
$$ \begin{equation*} SO _{2(a q)}+2 H_2 O _{(j)} \longrightarrow SO _{4(a q)}^{2-}+4 H _{(a q)}^{+}+2 e^{-} \tag{i} \end{equation*} $$
The reduction half reaction is:
$ Cl _{2(s)} \longrightarrow Cl _{(a q)}^{-} $
The chlorine atoms are balanced as:
$ \stackrel{0}C _{2(s)} \longrightarrow \stackrel{-1}C _{(a q)}^{-} $
The oxidation number is balanced by adding electrons
$$ \begin{equation*} Cl _{2(s)}+2 e^{-} \longrightarrow 2 Cl _{(a q)}^{-} \tag{ii} \end{equation*} $$
The balanced chemical equation can be obtained by adding equation (i) and (ii) as:
$ Cl _{2(s)}+SO _{2(a q)}+2 H_2 O _{(f)} \longrightarrow 2 Cl _{(a q)}^{-}+SO _{4(a q)}^{2-}+4 H _{(a q)}^{+} $
8.24 Refer to the periodic table given in your book and now answer the following questions:
(a) Select the possible non metals that can show disproportionation reaction.
(b) Select three metals that can show disproportionation reaction.
Show Answer
Answer
In disproportionation reactions, one of the reacting substances always contains an element that can exist in at least three oxidation states.
(a) $P, Cl$, and $S$ can show disproportionation reactions as these elements can exist in three or more oxidation states.
(b) $Mn, Cu$, and $Ga$ can show disproportionation reactions as these elements can exist in three or more oxidation states.
8.25 In Ostwald’s process for the manufacture of nitric acid, the first step involves the oxidation of ammonia gas by oxygen gas to give nitric oxide gas and steam. What is the maximum weight of nitric oxide that can be obtained starting only with 10.00 g. of ammonia and $20.00 \mathrm{~g}$ of oxygen?
Show Answer
Answer
The balanced chemical equation for the given reaction is given as:
$$ \begin{matrix} 4 NH _{3(g)}+5 O _{2(g)} & 4 NO _{(g)} & +6 H_2 O _{(g)} \\ 4 \times 17 g & 5 \times 32 g & 4 \times 30 g \quad 6 \times 18 g \\ =68 g \quad=160 g & =120 g \quad=108 g \end{matrix} $$
Thus, $68 g$ of $NH_3$ reacts with $160 g$ of $O_2$.
Therefore, $10 g$ of $NH_3$ reacts with $\frac{160 \times 10}{68} g$ of $O_2$, or $23.53 g$ of $O_2$.
But the available amount of $O_2$ is $20 g$.
Therefore, $O_2$ is the limiting reagent (we have considered the amount of $O_2$ to calculate the weight of nitric oxide obtained in the reaction).
Now, $160 g$ of $O_2$ gives $120 g$ of $NO$.
Therefore, $20 g$ of $O_2$ gives $\frac{120 \times 20}{160} g$ of $N$, or $15 g$ of $NO$.
Hence, a maximum of $15 g$ of nitric oxide can be obtained.
8.26 Using the standard electrode potentials given in the Table 8.1, predict if the reaction between the following is feasible:
(a) $\mathrm{Fe}^{3+}(\mathrm{aq})$ and $\mathrm{I}^{-}(\mathrm{aq})$
(b) $\mathrm{Ag}^{+}(\mathrm{aq})$ and $\mathrm{Cu}(\mathrm{s})$
(c) $\mathrm{Fe}^{3+}$ (aq) and $\mathrm{Cu}(\mathrm{s})$
(d) $\mathrm{Ag}(\mathrm{s})$ and $\mathrm{Fe}^{3+}(\mathrm{aq})$
(e) $\mathrm{Br_2}$ (aq) and $\mathrm{Fe}^{2+}(\mathrm{aq})$.
Show Answer
Answer
(a) The possible reaction between $Fe _{(a q)}^{3+}+I _{(a q)}^{-}$. is given by,
$2 Fe _{(a q)}^{3+}+2 I _{(a q)}^{-} \longrightarrow 2 Fe _{(a q)}^{2+}+I _{2(s)}$
Oxidation half equation : $\quad 2 I _{(x q)}^{-} \longrightarrow I _{2(s)}+2 e^{-} ; \quad E^{\circ}=-0.54 V$
Reduction half equation : $[Fe _{(cq)}^{3+}+e^{-} \longrightarrow Fe _{(cq)}^{2+}] \times 2 ; \quad E^{\circ}=+0.77 V$
$ 2 Fe _{(a q)}^{3+}+2 I _{(a q)}^{-} \longrightarrow 2 Fe _{(a q)}^{2+}+I _{2(s)} ; E^{\circ}=+0.23 V $
$E^{\circ}$ for the overall reaction is positive. Thus, the reaction between $Fe _{(a q)}^{3+}$ and $I _{(a q)}^{-}$is feasible.
(b) The possible reaction between $Ag _{(a q)}^{+}+Cu _{(s)}$ is given by,
$ 2 Ag _{(a q)}^{+}+Cu _{(s)} \longrightarrow 2 Ag _{(s)}+Cu _{(a q)}^{2+} $
Oxidation half equation : $\quad Cu _{(s)} \longrightarrow Cu _{(\text{aq })}^{2+}+2 e^{-} \quad ; E^{\circ}=-0.34 V$
$ \frac{\text{ Reduction half equation : }[Ag _{(a q)}^{+}+e^{-} \longrightarrow Ag _{(s)}] \times 2 \quad ; E^{\circ}=+0.80 V}{2 Ag _{(a q)}^{+}+Cu _{(s)} \longrightarrow 2 Ag _{(s)}+Cu^{2+} ; E^{\circ}=+0.46 V} $
$E^{\circ}$ positive for the overall reaction is positive. Hence, the reaction between $Ag _{(a q)}^{+}$and $Cu _{(s)}$ is feasible.
(c) The possible reaction between $Fe _{(a q)}^{3+}$ and $Cu _{(s)}$ is given by,
$ 2 Fe _{(a q)}^{3+}+Cu _{(s)} \longrightarrow 2 Fe _{(x)}^{2+}+Cu _{(a q)}^{2+} $
Oxidation half equation: $\quad Cu _{(s)} \longrightarrow Cu _{(a q)}^{2+}+2 e^{-} \quad ; E^{\circ}=-0.34 V$
Reduction half equation : $[Fe _{(\alpha q)}^{3+}+e^{-} \longrightarrow Fe _{(s)}^{2+}] \times 2 \quad ; E^{\circ}=+0.77 V$
$ 2 Fe _{(a q)}^{3+}+Cu _{(s)} \longrightarrow 2 Fe _{(s)}^{2+}+Cu _{(a q)}^{2+} ; E^{\circ}=+0.43 V $
$E^{\circ}$ positive for the overall reaction is positive. Hence, the reaction between $Fe _{(a q)}^{3+}$ and $Cu _{(s)}$ is feasible.
(d) The possible reaction between $Ag _{(s)}$ and $Fe _{(a q)}^{3+}$ is given by, $Ag _{(s)}+2 Fe _{(a q)}^{3+} \longrightarrow Ag _{(a q)}^{+}+Fe _{(a q)}^{2+}$
Oxidation half equation: $\quad Ag _{(x)} \longrightarrow Ag _{(a g)}^{+}+e^{-} \quad ; E^{\circ}=-0.80 V$
Reduction half equation : $Fe _{(a q)}^{3+}+e^{-} \longrightarrow Fe _{(a q)}^{2+} \quad ; E^{\circ}=+0.77 V$ $Ag _{(s)}+Fe _{(a q)}^{3+} \longrightarrow Ag _{(a q)}^{+}+Fe _{(a q)}^{2+} ; E^{\circ}=-0.03 V$
Here, $E^{\circ}$ for the overall reaction is negative. Hence, the reaction between $Ag _{(s)}$ and $Fe _{(a q)}^{3+}$ is not feasible.
(e) The possible reaction between $Br _{2(a q)}$ and $Fe _{(a q)}^{2+}$ is given by,
$Br _{2(s)}+2 Fe _{(a q)}^{2+} \longrightarrow 2 Br _{(a q)}^{-}+2 Fe _{(a q)}^{3+}$
Oxidation half equation : $.\quad Fe _{(a q)}^{2+} \longrightarrow Fe _{(a q)}^{3+}+e^{-}] \times 2 \quad ; E^{\circ}=-0.77 V$
Reduction half equation: $Br _{2(a q)}+2 e^{-} \longrightarrow 2 Br _{(a q)}^{-} \quad ; E^{\circ}=+1.09 V$
$ Br _{2(a q)}+2 Fe _{(a q)}^{2+} \longrightarrow 2 Br _{(a q)}^{-}+2 Fe _{(a q)}^{3+} ; E^{\circ}=-0.32 V $
Here, $E^{\circ}$ for the overall reaction is positive. Hence, the reaction between $Br _{2(a q)}$ and $Fe _{(a q)}^{2+}$ is feasible.
8.27 Predict the products of electrolysis in each of the following:
(i) An aqueous solution of $\mathrm{AgNO_3}$ with silver electrodes
(ii) An aqueous solution $\mathrm{AgNO_3}$ with platinum electrodes
(iii) A dilute solution of $\mathrm{H_2} \mathrm{SO_4}$ with platinum electrodes
(iv) An aqueous solution of $\mathrm{CuCl_2}$ with platinum electrodes.
Show Answer
Answer
(i) $AgNO_3$ ionizes in aqueous solutions to form $Ag^{+}$and $NO_3^{-}$ions.
On electrolysis, either $Ag^{+}$ions or $H_2 O$ molecules can be reduced at the cathode. But the reduction potential of $Ag^{+}$ions is higher than that of $H_2 O$.
$$ \begin{aligned} & Ag _{(o q)}^{+}+e^{-} \longrightarrow Ag _{(s)} ; E^{\circ}=+0.80 V \\ & 2 H_2 O _{(t)}+2 e^{-} \longrightarrow H _{2(g)}+2 OH _{(a q)}^{-} ; E^{\circ}=-0.83 V \end{aligned} $$
Hence, $Ag^{+}$ions are reduced at the cathode. Similarly, $Ag$ metal or $H_2 O$ molecules can be oxidized at the anode. But the oxidation potential of $Ag$ is higher than that of $H_2 O$ molecules.
$$ \begin{aligned} Ag _{(s)} & \longrightarrow Ag _{(a q)}^{+}+e^{-} \quad ; E^{\circ}=-0.80 V \\ 2 H_2 O _{(l)} & \longrightarrow O _{2(g)}+4 H _{(a q)}^{+}+4 e^{-} ; E^{\circ}=-1.23 V \end{aligned} $$
Therefore, Ag metal gets oxidized at the anode.
(ii) Pt cannot be oxidized easily. Hence, at the anode, oxidation of water occurs to liberate $O_2$. At the cathode, $Ag^{+}$ions are reduced and get deposited.
(iii) $H_2 SO_4$ ionizes in aqueous solutions to give $H^{+}$and $SO_4^{2-}$ ions.
$ H_2 SO _{4(a q)} \longrightarrow 2 H _{(a q)}^{+}+SO_4^{2-} _{(a q)} $
On electrolysis, either of $H^{+}$ions or $H_2 O$ molecules can get reduced at the cathode. But the reduction potential of $H^{+}$ions is higher than that of $H_2 O$ molecules.
$$ \begin{aligned} & 2 H _{(x q)}^{+}+2 e^{-} \longrightarrow H _{2(g)} ; E^{\circ}=0.0 V \\ & 2 H_2 O _{(a q)}+2 e^{-} \longrightarrow H _{2(g)}+2 OH _{(a q)}^{-} ; E^{\circ}=-0.83 V \end{aligned} $$
Hence, at the cathode, $H^{+}$ions are reduced to liberate $H_2$ gas.
On the other hand, at the anode, either of $SO_4^{2-}$ ions or $H_2 O$ molecules can get oxidized. But the oxidation of $SO_4^{2-}$ involves breaking of more bonds than that of $H_2 O$ molecules. Hence, $SO_4^{2-}$ ions have a lower oxidation potential than $H_2 O$. Thus, $H_2 O$ is oxidized at the anode to liberate $O_2$ molecules.
(iv) In aqueous solutions, $CuCl_2$ ionizes to give $Cu^{2+}$ and $Cl^{1 e^{E}}$ ions as:
$ CuCl _{2(a q)} \longrightarrow Cu _{(a q)}^{2+}+2 Cl _{(a q)}^{-} $
On electrolysis, either of $Cu^{2+}$ ions or $H_2 O$ molecules can get reduced at the cathode. But the reduction potential of $Cu^{2+}$ is more than that of $H_2 O$ molecules.
$$ \begin{aligned} & Cu _{(a q)}^{2+}+2 e^{-} \longrightarrow Cu _{(a q)} ; E^{\circ}=+0.34 V \\ & H_2 O _{(l)}+2 e^{-} \longrightarrow H _{2(g)}+2 OH^{-} ; E^{\circ}=-0.83 V \end{aligned} $$
Hence, $Cu^{2+}$ ions are reduced at the cathode and get deposited.
Similarly, at the anode, either of $Cl^{-}$ or $H_2 O$ is oxidized. The oxidation potential of $H_2 O$ is higher than that of $Cl^{-}$.
$$ \begin{aligned} & 2 Cl _{(a q)}^{-} \longrightarrow Cl _{2(g)}+2 e^{-} \quad ; E^{\circ}=-1.36 V \\ & 2 H_2 O _{(l)} \longrightarrow O _{2(g)}+4 H _{(a q)}^{+}+4 e^{-} ; E^{\circ}=-1.23 V \end{aligned} $$
But oxidation of $H_2 O$ molecules occurs at a lower electrode potential than that of $Cl^{{-}}$ions because of over-voltage (extra voltage required to liberate gas). As a result, $Cl^{-}$ ions are oxidized at the anode to liberate $Cl_2$ gas.
8.28 Arrange the following metals in the order in which they displace each other from the solution of their salts.
$\mathrm{Al}, \mathrm{Cu}, \mathrm{Fe}, \mathrm{Mg}$ and $\mathrm{Zn}$.
Show Answer
Answer
A metal of stronger reducing power displaces another metal of weaker reducing power from its solution of salt.
The order of the increasing reducing power of the given metals is $Cu<Fe<Zn<Al<Mg$.
Hence, we can say that $Mg$ can displace $Al$ from its salt solution, but $Al$ cannot displace $Mg$.
Thus, the order in which the given metals displace each other from the solution of their salts is given below:
$Mg>Al>Zn>Fe,>Cu$
8.29 Given the standard electrode potentials,
$\mathrm{K}^{+} / \mathrm{K}=-2.93 \mathrm{~V}, \mathrm{Ag}^{+} / \mathrm{Ag}=0.80 \mathrm{~V}$,
$\mathrm{Hg}^{2+} / \mathrm{Hg}=0.79 \mathrm{~V}$
$\mathrm{Mg}^{2+} / \mathrm{Mg}=-2.37 \mathrm{~V} . \mathrm{Cr}^{3+} / \mathrm{Cr}=-0.74 \mathrm{~V}$
arrange these metals in their increasing order of reducing power.
Show Answer
Answer
The lower the electrode potential, the stronger is the reducing agent. Therefore, the increasing order of the reducing power of the given metals is $Ag<Hg<Cr<Mg<K$.
8.30 Depict the galvanic cell in which the reaction $\mathrm{Zn}(\mathrm{s})+2 \mathrm{Ag}^{+}(\mathrm{aq}) \rightarrow \mathrm{Zn}^{2+}(\mathrm{aq})+2 \mathrm{Ag}(\mathrm{s})$ takes place, Further show:
(i) which of the electrode is negatively charged,
(ii) the carriers of the current in the cell, and
(iii) individual reaction at each electrode.
Show Answer
Answer
The galvanic cell corresponding to the given redox reaction can be represented as:
$Zn|Zn _{(a q)}^{2+} | Ag _{(a q)}^{+}| Ag$
(i) $Zn$ electrode is negatively charged because at this electrode, $Zn$ oxidizes to $Zn^{2+}$ and the leaving electrons accumulate on this electrode.
(ii) Ions are the carriers of current in the cell.
(iii) The reaction taking place at $Zn$ electrode can be represented as:
$ Zn _{(s)} \longrightarrow Zn _{(a q)}^{2+}+2 e^{-} $
And the reaction taking place at $Ag$ electrode can be represented as:
$Ag _{(a q)}^{+}+e^{-} \longrightarrow Ag _{(s)}$










