Chapter 11 Dual Nature of Radiation and Matter
Multiple Choice Questions (MCQs)
1. A particle is dropped from a height $H$. The de-Broglie wavelength of the particle as a function of height is proportional to
(a) $H$
(b) $H^{1 / 2}$
(c) $H^{0}$
(d) $H^{-1 / 2}$
Show Answer
Thinking Process
The de-broglie wavelength $\boldsymbol{\lambda}$ is given by $\boldsymbol{\lambda}=\frac{h}{m v}$.
Answer
(d) Velocity of a body falling from a height $H$ is given by
$$ v=\sqrt{2 g H} $$
We know that de-broglie wavelength
$$ \lambda=\frac{h}{m v}=\frac{h}{m \sqrt{2 g H}} \Rightarrow=\frac{h}{m \sqrt{2 g} \sqrt{H}} $$
Here, $\frac{h}{m \sqrt{2 g}}$ is a constant $\phi$ say ’ $K$ ‘.
So,
$$ \begin{aligned} & \lambda=K \frac{1}{\sqrt{H}} \Rightarrow \lambda \propto \frac{1}{\sqrt{H}} \\ & \lambda \propto H^{-1 / 2} \end{aligned} $$
2. The wavelength of a photon needed to remove a proton from a nucleus which is bound to the nucleus with $1 MeV$ energy is nearly $\newline$
(a) $1.2 nm$ $\newline$
(b) $1.2 \times 10^{-3} nm$ $\newline$
(c) $1.2 \times 10^{-6} nm$ $\newline$
(d) $1.2 \times 10 nm$ $\newlin
Thinking Process
Energy of a photon is $E=\frac{h c}{\lambda}$, where $\lambda$ is the minimum wavelength of the photon required to eject the proton from nucleus.
Show Answer
Answer
(b) Given in the question,
Energy of a photon, $E=1 MeV \Rightarrow=10^{6} eV$
Now,
$h c=1240 eVnm$
Now,
$E=\frac{h c}{\lambda}$
$\Rightarrow$
$$ l=\frac{h c}{E}=\frac{1240 eVnm}{10^{6} eV} $$
$$ =1.24 \times 10^{-3} nm $$
3. Consider a beam of electrons (each electron with energy $E_0$ ) incident on a metal surface kept in an evacuated chamber. Then,
(a) no electrons will be emitted as only photons can emit electrons
(b) electrons can be emitted but all with an energy, $E_0$
(c) electrons can be emitted with any energy, with a maximum of $E_0-\phi$ ( $\phi$ is the work function)
(d) electrons can be emitted with any energy, with a maximum of $E_0$
Show Answer
Answer
(d) When a beam of electrons of energy $E_0$ is incident on a metal surface kept in an evacuated chamber electrons can be emitted with maximum energy $E_0$ (due to elastic collision) and with any energy less than $E_0$, when part of incident energy of electron is used in liberating the electrons from the surface of metal.
4. Consider figure given below. Suppose the voltage applied to $A$ is increased. The diffracted beam will have the maximum at a value of $\theta$ that
(a) will be larger than the earlier value
(b) will be the same as the earlier value
(c) will be less than the earlier value
(d) will depend on the target
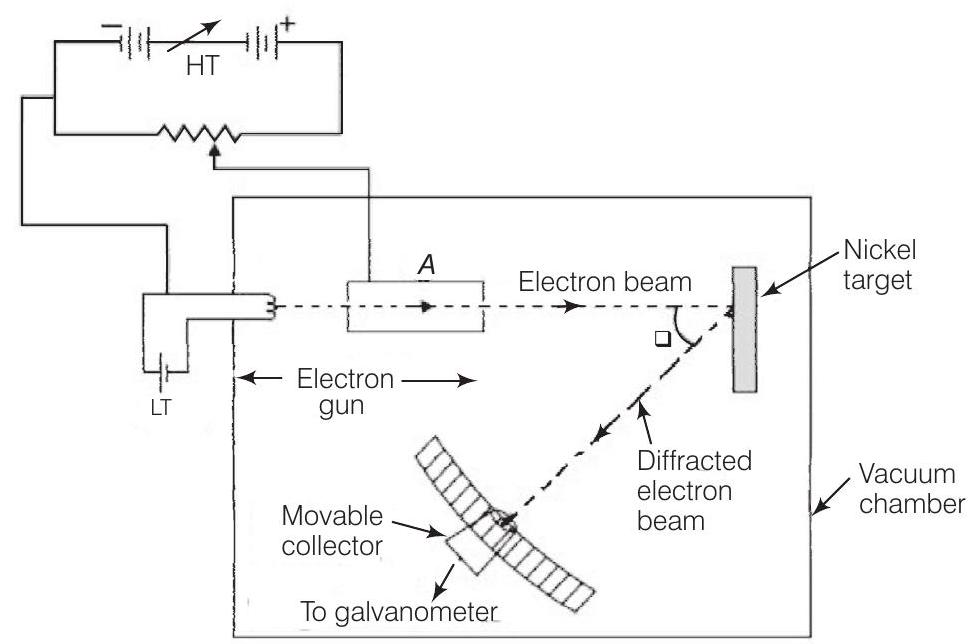
Show Answer
Thinking Process
The figure given here shows the Davisson-Germer experiment which was held to verify the wave nature of electrons.
Answer
(c) In Davisson-Germer experiment, the de-Broglie wavelength associated with electron is
$$ \lambda=\frac{12.27}{\sqrt{V}} \AA $$
where $V$ is the applied voltage.
If there is a maxima of the diffracted electrons at an angle $\theta$, then
$$ 2 d \sin \theta=\lambda $$
From(i.), we note that if $V$ is inversely proportional to the wavelength $\lambda$. i.e., $V$ will increase with the decrease in the $\lambda$.
From Eq. (ii), we note that wavelength $\lambda$ is directly proportional to $\sin \theta$ and hence $\theta$. So, with the decrease in $\lambda, \theta$ will also decrease.
Thus, when the voltage applied to $A$ is increased. The diffracted beam will have the maximum at a value of $\theta$ that will be less than the earlier value.
5. A proton, a neutron, an electron and an $\alpha$-particle have same energy. Then, their de-Broglie wavelengths compare as $\newline$
(a) $\lambda_{p}=\lambda_{n}>\lambda_{e}>\lambda_{\alpha}$ $\newline$
(b) $\lambda_{\alpha}<\lambda_{p}=\lambda_{n}>\lambda_{e}$ $\newline$
(c) $\lambda_{e}<\lambda_{p}=\lambda_{n}>\lambda_{\alpha}$ $\newline$
(d) $\lambda_{e}=\lambda_{p}=\lambda_{n}=\lambda_{\alpha}$ $\newline$
Show Answer
Thinking Process
The energy of any particle can be given by $K=\frac{1}{2} m v^{2}$
$\Rightarrow \quad m v=\sqrt{2 m k}$
Also, de-Broglie wavelength is given by
$$ \lambda=\frac{h}{m v} $$
Now, relation between energy and wavelength of any particle is given by putting the value of Eq. (i) in Eq. (ii)
$$ \lambda=\frac{h}{\sqrt{2 m k}} $$
Answer
(b) We know that the relation between $\lambda$ and $K$ is given by
$$ \lambda=\frac{h}{\sqrt{2 m k}} $$
Here, for the given value of energy $K, \frac{h}{\sqrt{2 k}}$ is a constant.
Thus, $\quad \lambda \propto \frac{1}{\sqrt{m}}$
$\therefore \quad \lambda_{p}: \lambda_{n}: \lambda_{e}: \lambda_{\alpha}$
$\Rightarrow \quad=\frac{1}{\sqrt{m_{p}}}: \frac{1}{\sqrt{m_{n}}}: \frac{1}{\sqrt{m_{e}}}: \frac{1}{\sqrt{m_{\alpha}}}$
Since, $\quad m_{p}=m_{n}$, hence $\boldsymbol{\lambda}{p}=\lambda{n}$
As, $\quad m_{\alpha}>m_{p}$, therefore $\lambda_{\alpha}<\lambda_{p}$
As, $\quad m_{e}<m_{n}$, therefore $\lambda_{e}>\lambda_{n}$
Hence, $\quad \lambda_{\alpha}<\lambda_{p}=\lambda_{n}<\lambda_{e}$
6. An electron is moving with an initial velocity $\mathbf{v}=v_0 \hat{\mathbf{i}}$ and is in a magnetic field $\mathbf{B}=B_0 \hat{\mathbf{j}}$. Then, it’s de-Broglie wavelength
(a) remains constant
(b) increases with time
(c) decreases with time
(d) increases and decreases periodically
Show Answer
Answer
(a) Given,
$$ \mathbf{v}=v_0 \hat{\mathbf{i}} \Rightarrow \mathbf{B}=B_0 \hat{\mathbf{j}} $$
Force on moving electron due to magnetic field is, $F=-e(v \times B)$
$$ =-e[v_0 \mathbf{i} \times B_0 \mathbf{j}] \Rightarrow=-e v_0 B_0 \mathbf{k} $$
As this force is perpendicular to $\mathbf{v}$ and $\mathbf{B}$, so the magnitude of $\mathbf{v}$ will not change, i.e., momentum $(=m v)$ will remain constant in magnitude. Hence,
de-Broglie wavelength $\lambda=\frac{h}{m v}$ remains constant.
7. An electron (mass $m$ ) with an initial velocity $\mathbf{v}=v_0 \mathbf{i}(v_0>0)$ is in an electric field $\mathbf{E}=-E_0 \hat{\mathbf{i}}(E_0=.$ constant $.>0)$. It’s de-Broglie wavelength at time $t$ is given by $\newline$
(a) $\frac{\lambda_0}{1+\frac{e E_0}{m} \frac{t}{v_0}}$ $\newline$
(b) $\lambda_0 1+\frac{e E_0 t}{m v_0}$ $\newline$ (c) $\lambda_0$ $\newline$
(d) $\lambda_0 t $ $\newline $
Show Answer
Thinking Process
de - Broglie wavelength is given by $\boldsymbol{\lambda}=\frac{h}{m v}$
Answer
(a) Initial de-Broglie wavelength of electron,
$$ \lambda_0=\frac{h}{m v_0} $$
Force on electron in electric field,
$$ \mathbf{F}=-e \mathbf{E}=-e[-E_0 \hat{\mathbf{i}}]=e E_0 \hat{\mathbf{i}} $$
Acceleration of electron
$$ a=\frac{\mathbf{F}}{m}=\frac{e E_0 \hat{\mathbf{i}}}{m} $$
Velocity of electron after time $t$,
$$ \begin{aligned} v & =v_0 \hat{\mathbf{i}}+\frac{e E_0 \hat{\mathbf{i}}}{m} t=v_0+\frac{e E_0}{m} t \hat{\mathbf{i}} \\ & =v_0 1+\frac{e E_0}{m v_0} t \hat{\mathbf{i}} \end{aligned} $$
de - Broglie wavelength associated with electron at time $t$ is
$$ \begin{aligned} & \lambda=\frac{h}{m v} \\ & =\frac{h}{m v_0 1+\frac{e E_0}{m v_0} t}=\frac{\lambda_0}{1+\frac{e E_0}{m v_0} t} \\ & \because \lambda_0=\frac{h}{m v_0} \end{aligned} $$
8. An electron (mass $m$ ) with an initial velocity $\mathbf{v}=v_0 \hat{\mathbf{i}}$ is in an electric field $\mathbf{E}=E_0 \hat{\mathbf{j}}$. If $\lambda_0=h / m v_0$, it’s de-Broglie wavelength at time $t$ is given by $\newline$
(a) $\lambda_0$ $\newline$
(b) $\lambda_0 \sqrt{1+\frac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}}}$ $\newline$
(c) $\frac{\lambda_0}{\sqrt{1+\frac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}}}}$ $\newline$
(d) $\frac{\lambda_0}{1+\frac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}}}$ $\newline$
Show Answer
Answer
(c) Initial de - Broglie wavelength of electron,
$$ \lambda_0=\frac{h}{m v_0} $$
Force on electron in electric field,
$$ F=-e E=-e E_0 \hat{j} $$
Acceleration of electron,
$$ a=\frac{F}{m}=\frac{e E_0 \hat{j}}{m} $$
It is acting along negative $y$-axis.
The initial velocity of electron along $x$-axis, $x_0=v_0 \hat{\mathbf{i}}$. Initial velocity of electron along $y$-axis,
$$ y_0=0 . $$
Velocity of electron after time $t$ along $x$-axis, $x =_0 \hat{\mathbf{i}}$
Velocity of electron after timet along $y$-axis,
$$ y=0+-\frac{e E_0}{m} \hat{\mathbf{j}} t=-\frac{e E_0}{m} t \hat{\mathbf{j}} $$
Magnitude of velocity of electron after time $t$ is
$$ v =\sqrt{v_x^{2}+v_y^{2}}=\sqrt{v_0^{2}+\frac{-e E_0}{m} t^{2}} \newline $$ $$\Rightarrow =v_0 \sqrt{1+\frac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}}} \newline $$ $$\text { de-Broglie wavelength, } \lambda^{\prime} =\frac{h}{m v} \newline $$ $$ =\frac{h}{m v_0 \sqrt{1+e^{2} E_0^{2} t^{2} /(m^{2} v_0^{2})}} \newline $$ $$ =\frac{\lambda_0}{\sqrt{1+e^{2} E_0^{2} t^{2} / m^{2} v_0^{2}}} $$
Multiple Choice Questions (More Than One Options)
9. Relativistic corrections become necessary when the expression for the kinetic energy $\frac{1}{2} m v^{2}$, becomes comparable with $m c^{2}$, where $m$ is the mass of the particle. At what de-Broglie wavelength, will relativistic corrections become important for an electron?
(a) $\lambda=10 nm$
(b) $\lambda=10^{-1} nm$
(c) $\lambda=10^{-4} nm$
(d) $\lambda=10^{-6} nm$
Show Answer
Thinking Process
The de-Broglie wavelength at which relativistic corrections become important must be greater than speed of light i.e., $3 \times 10^{8} m / s$.
Answer
$(c, d)$
de-Broglie wavelength
Here,
$$ \begin{aligned} & \lambda=\frac{h}{m v} \Rightarrow v=\frac{h}{m \lambda} \\ & h=6.6 \times 10^{-34} Js \end{aligned} $$
and for electron,
Now consider each option one by one
(a)
$$ \lambda_1=10 nm=10 \times 10^{-9} m=10^{-8} m $$
$$ \begin{matrix} \Rightarrow & v_1=\frac{6.6 \times 10^{-34}}{(9 \times 10^{-31}) \times 10^{-8}} \\ \Rightarrow & =\frac{2.2}{3} \times 10^{5} \approx 10^{5} m / s \end{matrix} $$
(b) $\lambda_2=10^{-1} nm=10^{-1} \times 10^{-9} m=10^{-10} m$
$\Rightarrow \quad v_2=\frac{6.6 \times 10^{-34}}{(9 \times 10^{-31}) \times 10^{-10}} \approx 10^{7} m / s$
(c) $\lambda_3=10^{-4} nm=10^{-4} \times 10^{-9} m=10^{-13} m$
$\Rightarrow \quad v_3=\frac{6.6 \times 10^{-34}}{(9 \times 10^{-31}) \times 10^{-13}} \approx 10^{10} m / s$
(d) $\lambda_4=10^{-6} nm=10^{-6} \times 10^{-9} m=10^{-15} m$
$\Rightarrow \quad v_4=\frac{6.6 \times 10^{-34}}{9 \times 10^{-31} \times 10^{-15}} \approx 10^{12} m / s$
Thus, options (c) and (d) are correct as $v_3$ and $v_4$ is greater than $3 \times 10^{8} m / s$.
10. Two particles $A_1$ and $A_2$ of masses $m_1, m_2(m_1>m_2)$ have the same de-Broglie wavelength. Then,
(a) their momenta are the same
(b) their energies are the same
(c) energy of $A_1$ is less than the energy of $A_2$
(d) energy of $A_1$ is more than the energy of $A_2$
Show Answer
Answer
(a, c)
de-Broglie wavelength $\lambda=\frac{h}{m v}$
where, $m v=p$ (moment)
$\Rightarrow$
$$ \lambda=\frac{h}{p} \Rightarrow p=\frac{h}{\lambda} $$
Here, $h$ is a constant.
So,
$$ \begin{gathered} p \propto \frac{1}{\lambda} \Rightarrow \frac{p_1}{p_2}=\frac{\lambda_2}{\lambda_1} \\ (\lambda_1=\lambda_2)=\lambda \\ \frac{p_1}{p_2}=\frac{\lambda}{\lambda}=1 \Rightarrow p_1=p_2 \end{gathered} $$
But
Then,
Thus, their momenta is same.
Also,
$$ \begin{aligned} E & =\frac{1}{2} m v^{2}=\frac{1}{2} \frac{m v^{2} \times m}{m} \\ & =\frac{1}{2} \frac{m^{2} v^{2}}{m}=\frac{1}{2} \frac{p^{2}}{m} \end{aligned} $$
Here, $p$ is constant
$$ E \propto \frac{1}{m} $$
$$ \frac{E_1}{E_2}=\frac{m_2}{m_1}<1 \Rightarrow E_1<E_2 $$
11. The de-Broglie wavelength of a photon is twice, the de-Broglie wavelength of an electron. The speed of the electron is $v_{e}=\frac{c}{100}$. Then, $\newline$
(a) $\frac{E_{e}}{E_{p}}=10^{-4}$ $\newline$
(b) $\frac{E_{e}}{E_{p}}=10^{-2}$ $\newline$
(c) $\frac{p_{e}}{m_{e} c}=10^{-2}$ $\newline$
(d) $\frac{p_{e}}{m_{e} c}=10^{-4}$ $\newline$
Show Answer
Answer
( $b, c$ )
Suppose, Mass of electron $=m_{e}, \quad$ Mass of photon $=m_{p}$,
Velocity of electron $=v_{e}$ and $\quad$ Velocity of photon $=v_{p}$
Thus, for electron, de-Broglie wavelength
$$ \begin{aligned} \lambda_{e} & =\frac{h}{m_{e} v_{e}} \\ & =\frac{h}{m_{e}(c / 100)}=\frac{100 h}{m_{e} c} \text { (given) } \end{aligned} $$
Kinetic energy,
$$ E_{e}=\frac{1}{2} m_{e} v_e^{2} $$
$\Rightarrow \quad m_{e} v_{e}=\sqrt{2 E_{e} m_{e}}$
$$ \text { so, } \quad \lambda_{e}=\frac{h}{m_{e} v_{e}}=\frac{h}{\sqrt{2 m_{e} E_{e}}} $$
$\Rightarrow \quad E_{e}=\frac{h^{2}}{2 \lambda_e^{2} m_{e}}$
For photon of wavelength $\lambda_{p}$, energy
$$ E_{p}=\frac{h c}{\lambda_{p}}=\frac{h c}{2 \lambda_{e}} $$
$$ \begin{aligned} & \therefore \quad \frac{E_{p}}{E_{e}}=\frac{h c}{2 \lambda_{e}} \times \frac{2 \lambda_e^{2} m_{e}}{h^{2}} \\ & =\frac{\lambda_{e} m_{e} c}{h}=\frac{100 h}{m_{e} c} \times \frac{m_{e} c}{h}=100 \\ & \text { So, } \\ & \text { For electron, } \\ & \text { So, } \\ & \frac{E_{e}}{E_{p}}=\frac{1}{100}=10^{-2} \\ & p_{e}=m_{e} v_{e}=m_{e} \times c / 100 \\ & \frac{p_{e}}{m_{e} c}=\frac{1}{100}=10^{-2} \end{aligned} $$
12. Photons absorbed in matter are converted to heat. A source emitting $n$ photon/sec of frequency $v$ is used to convert $1 kg$ of ice at $0^{\circ} C$ to water at $0^{\circ} C$. Then, the time $T$ taken for the conversion
(a) decreases with increasing $n$, with $v$ fixed
(b) decreases with $n$ fixed, $v$ increasing
(c) remains constant with $n$ and $v$ changing such that $n v=$ constant
(d) increases when the product $n v$ increases
Show Answer
Answer
$(a, b, c)$
Energy spent to convert ice into water
$$ \begin{aligned} & =\text { mass } \times \text { latent heat } \\ & =m L=(1000 g) \times(80 cal / g) \\ & =80000 cal \end{aligned} $$
Energy of photons used $=n T \times E=n T \times h \nu$
So,
$$ n T h \nu=m L \Rightarrow T=\frac{m L}{n h v} $$
$\therefore \quad T \propto \frac{1}{n}$, when $v$ is constant.
$T \propto \frac{1}{v}$, when $n$ is fixed.
$\Rightarrow \quad T \propto \frac{1}{n v}$.
Thus, $T$ is constant, if $n v$ is constant.
13. A particle moves in a closed orbit around the origin, due to a force which is directed towards the origin. The de-Broglie wavelength of the particle varies cyclically between two values $\lambda_1, \lambda_2$ with $\lambda_1>\lambda_2$. Which of the following statement are true?
(a) The particle could be moving in a circular orbit with origin as centre
(b) The particle could be moving in an elliptic orbit with origin as its focus
(c) When the de-Broglie wavelength is $\lambda_1$, the particle is nearer the origin than when its value is $\lambda_2$
(d) When the de-Broglie wavelength is $\lambda_2$, the particle is nearer the origin than when its value is $\lambda_1$
Show Answer
Answer
($b, d)$
The de-Broglie wavelength of the particle can be varying cyclically between two values $\lambda_1$ and $\lambda_2$, if particle is moving in an elliptical orbit with origin as its one focus.
Consider the figure given below
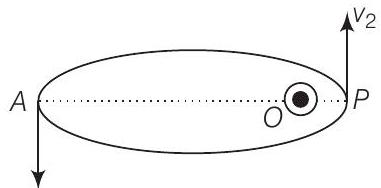
Let $v_1, v_2$ be the speed of particle at $A$ and $B$ respectively and origin is at focus $O$. If $\lambda_1, \lambda_2$ are the de-Broglie wavelengths associated with particle while moving at $A$ and $B$ respectively. Then,
and
$$ \begin{aligned} & \lambda_1=\frac{h}{m v_1} \\ & \lambda_2=\frac{h}{m v_2} \end{aligned} $$
$$ \begin{matrix} \therefore & \frac{\lambda_1}{\lambda_2}=\frac{v_2}{v_1} \\ \text { since } & \lambda_1>\lambda_2 \\ \therefore & v_2>v_1 \end{matrix} $$
By law of conservation of angular momentum, the particle moves faster when it is closer to focus.
From figure, we note that origin $O$ is closed to $P$ than $A$.
Very Short Answer Type Questions
14. A proton and an $\alpha$-particle are accelerated, using the same potential difference. How are the de-Broglie wavelengths $\lambda_{p}$ and $\lambda_{\alpha}$ related to each other?
Show Answer
Thinking Process
Here, since both proton and $\boldsymbol{\alpha}$-particle use the same potential difference, thus they are taken as constant.
Answer
As,
$$ \begin{aligned} \lambda & =\frac{h}{\sqrt{2 m q v}} \\ \lambda & \propto \frac{1}{\sqrt{m q}} \\ \frac{\lambda_{p}}{\lambda_{\alpha}} & =\frac{\sqrt{m_{\alpha} q_{\alpha}}}{\sqrt{m_{p} q_{p}}}=\frac{\sqrt{4 m_{p} \times 2 e}}{\sqrt{m_{p} \times e}}=\sqrt{8} \end{aligned} $$
$$ \therefore \quad \lambda_{p}=\sqrt{8} \lambda_{\alpha} $$
i.e., wavelength of proton is $\sqrt{8}$ times wavelength of $\alpha$-particle.
15. (i) In the explanation of photoeletric effect, we assume one photon of frequency $v$ collides with an electron and transfers its energy. This leads to the equation for the maximum energy $E_{\max }$ of the emitted electron as
$$ E_{\max }=h \nu-\phi_0 $$
where $\phi_0$ is the work function of the metal. If an electron absorbs 2 photons (each of frequency $\nu$ ), what will be the maximum energy for the emitted electron?
(ii) Why is this fact (two photon absorption) not taken into consideration in our discussion of the stopping potential?
Show Answer
Answer
(i) Here it is given that, an electron absorbs 2 photons each of frequency $v$ then $v^{\prime}=2 v$ where, $v^{\prime}$ is the frequency of emitted electron.
Given, $\quad E_{\max }=h \nu-\phi_0$
Now, maximum energy for emitted electrons is
$$ E_{\max }^{\prime}=h(2 v)-\phi_0=2 h \nu-\phi_0 $$
(ii) The probability of absorbing 2 photons by the same electron is very low. Hence, such emission will be negligible.
16. There are materials which absorb photons of shorter wavelength and emit photons of longer wavelength. Can there be stable substances which absorb photons of larger wavelength and emit light of shorter wavelength.
Show Answer
Answer
According to first statement, when the materials which absorb photons of shorter wavelength has the energy of the incident photon on the material is high and the energy of emitted photon is low when it has a longer wavelength.
But in second statement, the energy of the incident photon is low for the substances which has to absorb photons of larger wavelength and energy of emitted photon is high to emit light of shorter wavelength. This means in this statement material has to supply the energy for the emission of photons.
But this is not possible for a stable substances.
17. Do all the electrons that absorb a photon come out as photoelectrons?
Show Answer
Answer
In photoelectric effect, we can observe that most electrons get scattered into the metal by absorbing a photon.
Thus, all the electrons that absorb a photon doesn’t come out as photoelectron. Only a few come out of metal whose energy becomes greater than the work function of metal.
18. There are two sources of light, each emitting with a power of 100 W. One emits $X$-rays of wavelength $1 nm$ and the other visible light at $500 nm$. Find the ratio of number of photons of $X$-rays to the photons of visible light of the given wavelength?
Show Answer
Answer
Suppose wavelength of $X$-rays is $\lambda_1$ and the wavelength of visible light is $\lambda_2$.
Given, $\quad P=100 W$
and
$\lambda_1=1 nm$
$\lambda_2=500 nm$
Also, $n_1$ and $n_2$ represents number of photons of X-rays and visible light emitted from the two sources per sec.
So,
$\frac{E}{t}=P=n_1 \frac{h c}{\lambda_1}=n_2 \frac{h c}{\lambda_2}$
$\Rightarrow$
$\frac{n_1}{\lambda_1}=\frac{n_2}{\lambda_2}$
$\Rightarrow$
$\frac{n_1}{n_2}=\frac{\lambda_1}{\lambda_2}=\frac{1}{500}$
Short Answer Type Questions
19. Consider figure for photoemission. How would you reconcile with momentum-conservation? Note light (photons) have momentum in a different direction than the emitted electrons.
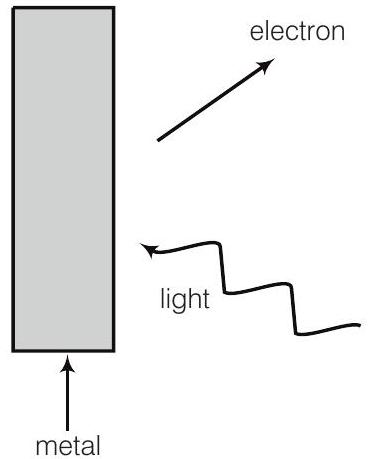
Show Answer
Answer
During photoelectric emission, the momentum of incident photon is transferred to the metal. At microscopic level, atoms of a metal absorb the photon and its momentum is transferred mainly to the nucleus and electrons.
The excited electron is emitted. Therefore, the conservation of momentum is to be considered as the momentum of incident photon transferred to the nucleus and electrons.
20. Consider a metal exposed to light of wavelength $600 nm$. The maximum energy of the electron doubles when light of wavelength $400 nm$ is used. Find the work function in eV.
Thinking Process
Maximum energy $=h \nu-\phi$
Show Answer
Answer
Given,
For the first condition,
Wavelength of light $\lambda=600 nm$
and for the second condition,
Wavelength of light $\lambda^{\prime}=400 nm$
Also, maximum kinetic energy for the second condition is equal to the twice of the kinetic energy in first condition.
$$ \begin{matrix} \text { i.e., } & K_{\max }^{\prime} & =2 K_{\max } \\ \text { Here, } & K_{\max }^{\prime} & =\frac{h c}{\lambda}-\phi \\ \Rightarrow & 2 K_{\max } & =\frac{h c}{\lambda^{\prime}}-\phi_0 \\ \Rightarrow & 2 \frac{1230}{600}-\phi & =\frac{1230}{400}-\phi \\ \Rightarrow & \phi & =\frac{1230}{1200}=1.02 eV \end{matrix} $$
21. Assuming an electron is confined to a $1 nm$ wide region, find the uncertainty in momentum using Heisenberg uncertainty principle $(\Delta x \times \Delta p \approx h)$. You can assume the uncertainty in position $\Delta x$ as $1 nm$. Assuming $p \approx \Delta p$, find the energy of the electron in electronvolts.
Show Answer
Answer
Here, $\Delta x=1 nm=10^{-9} m, \Delta p=$ ?
As $\Delta x \Delta p \approx h$
$$ \begin{matrix} \therefore & & \Delta p & =\frac{h}{\Delta x}=\frac{h}{2 \pi \Delta x} \\ \Rightarrow & & =\frac{6.62 \times 10^{-34} Js}{2 \times(22 / 7)(10^{-9}) m} \\ & & =1.05 \times 10^{-25} kg m / s \\ \text { Energy, } & E & =\frac{p^{2}}{2 m}=\frac{(\Delta p)^{2}}{2 m} \\ & & =\frac{(1.05 \times 10^{-25})^{2}}{2 \times 9.1 \times 10^{-31}} J \\ \Rightarrow & & =\frac{(1.05 \times 10^{-25})^{2}}{2 \times 9.1 \times 10^{-31} \times 1.6 \times 10^{-19}} eV \\ & & =3.8 \times 10^{-2} eV . \end{matrix} $$
22. Two monochromatic beams $A$ and $B$ of equal intensity $I$, hit a screen. The number of photons hitting the screen by beam $A$ is twice that by beam $B$. Then, what inference can you make about their frequencies?
Show Answer
Answer
Suppose $n_{A}$ is the number of photons falling per second of beam $A$ and $n_{B}$ is the number of photons falling per second of beam $B$.
Thus,
$$ \begin{gathered} n_{A}=2 n_{B} \\ A=h v_{A} \\ B=h v_{B} \end{gathered} $$
Energy of falling photon of beam Energy of falling photon of beam
Now, according to question,
intensity of $A=$ intensity of $B$
$$ \begin{aligned} & \therefore \quad n_{A} h \nu_{A}=n_{B} h v_{E} \\ & \Rightarrow \quad \frac{v_{A}}{v_{B}}=\frac{n_{B}}{n_{A}}=\frac{n_{B}}{2 n_{B}}=\frac{1}{2} \\ & \Rightarrow \quad v_{B}=2 v_{A} \end{aligned} $$
Thus, from this relation we can infer that frequency of beam $B$ is twice of beam $A$.
23. Two particles $A$ and $B$ of de-Broglie wavelengths $\lambda_1$ and $\lambda_2$ combine to form a particle $C$. The process conserves momentum. Find the de-Broglie wavelength of the particle $C$. (The motion is one-dimensional)
Show Answer
Answer
Given from conservation of momentum,
$$ \begin{matrix} |C|=|A|+|B| \frac{h}{\lambda_{C}}=\frac{h}{\lambda_{A}}+\frac{h}{\lambda_{B}} \quad \newline \because \lambda=\frac{h}{m v}=\frac{h}{p} \Rightarrow p=\frac{h}{\lambda} \newline \\ \Rightarrow \frac{h}{\lambda_{C}}=\frac{h \lambda_{B}+h \lambda_{A}}{\lambda_{A} \lambda_{B}} \newline \\ \Rightarrow \frac{\lambda_{C}}{h}=\frac{\lambda_{A} \lambda_{B}}{h \lambda_{A}+h \lambda_{B}} \Rightarrow \lambda_{C}=\frac{\lambda_{A} \lambda_{B}}{\lambda_{A}+\lambda_{B}} \end{matrix} $$
Case I Suppose both $p_{A}$ and $p_{B}$ are positive, then
$$ \lambda_{C}=\frac{\lambda_{A} \lambda_{B}}{\lambda_{A}+\lambda_{B}} $$
Case II When both $p_{A}$ and $p_{B}$ are negative, then
$$ \lambda_{C}=\frac{\lambda_{A} \lambda_{B}}{\lambda_{A}+\lambda_{B}} $$
Case III When $p_{A}>0, p_{B}<0$ i.e., $p_{A}$ is positive and $p_{B}$ is negative,
$$ \begin{aligned} & \frac{h}{\lambda_{C}}=\frac{h}{\lambda_{A}}-\frac{h}{\lambda_{B}}=\frac{(\lambda_{B}-\lambda_{A}) h}{\lambda_{A} \lambda_{B}} \\ & \Rightarrow \quad \lambda_{C}=\frac{\lambda_{A} \lambda_{B}}{\lambda_{B}-\lambda_{A}} \end{aligned} $$
Case IV $\quad$ $p_{A}<0, p_{B}>0$, i.e., $p_{A}$ is negative and $p_{B}$ is positive,
$$ \begin{matrix} \therefore \frac{h}{\lambda_{C}} =\frac{-h}{\lambda_{A}}+\frac{h}{\lambda_{B}} \newline \\ \Rightarrow =\frac{(\lambda_{A}-\lambda_{B}) h}{\lambda_{A} \lambda_{B}} \Rightarrow \lambda_{C}=\frac{\lambda_{A} \lambda_{B}}{\lambda_{A}-\lambda_{B}} \end{matrix} $$
24. A neutron beam of energy $E$ scatters from atoms on a surface with a spacing $d=0.1 nm$. The first maximum of intensity in the reflected beam occurs at $\theta=30^{\circ}$. What is the kinetic energy $E$ of the beam in eV?
Show Answer
Answer
Given, $d=0.1 nm$,
Now, according to Bragg’s law
$$ \begin{matrix} \Rightarrow 2 d \sin \theta =n \lambda \Rightarrow 2 \times 0.1 \times \sin 30=1 \lambda \newline \\ \text { Now, } \lambda =0.1 nm \Rightarrow=10^{-10} m \newline \\ \Rightarrow \lambda =\frac{h}{m v}=\frac{h}{p} \newline \\ \Rightarrow p=\frac{h}{\lambda} =\frac{6.62 \times 10^{-34}}{10^{-10}} \newline \\ \text { Now, } =6.62 \times 10^{-24} kg-m / s \newline \\ KE =\frac{1}{2} m v^{2}=\frac{1}{2} \frac{m^{2} v^{2}}{m}=\frac{1}{2} \frac{p^{2}}{m} \newline \\ =\frac{1}{2} \times \frac{(6.62 \times 10^{-24})^{2}}{1.67 \times 10^{-27}} J \newline \\ =0.21 eV \end{matrix} $$
Long Answer Type Questions
25. Consider a thin target $(10^{-2} m.$ square, $10^{-3} m$ thickness) of sodium, which produces a photocurrent of $100 \mu A$ when a light of intensity 100 $W / m^{2}(\lambda=660 nm)$ falls on it. Find the probability that a photoelectron is produced when a photon strikes a sodium atom.
[Take density of $Na=0.97 kg / m^{3}$ ]
Show Answer
Thinking Process
Absorption of two photons by an atom depends on the probability of photoemission by a single photon on a single atom.
Answer
Given, $\Rightarrow$
Intensity, $$ \begin{aligned} A & =10^{-2} m^{2}=10^{-2} \times 10^{-2} m^{2} \\ & =10^{-4} m^{2} \\ d & =10^{-3} m \\ i & =100 \times 10^{-6} A=10^{-4} A \\ I & =100 W / m^{2} \\ \lambda & =660 nm=660 \times 10^{-9} m \\ \text { Pa } & =0.97 kg / m^{3} \\ \text { aber } & =6 \times 10^{26} kg \text { atom } \\ \text { rget } & =A \times d \\ & =10^{-4} \times 10^{-3} \\ & =10^{-7} m^{3} \end{aligned} $$
$$ \begin{aligned} \text { Avogadro’s number } & =6 \times 10^{26} kg \text { atom } \\ \text { Volume of sodium target } & =A \times d \end{aligned} $$
We know that $6 \times 10^{26}$ atoms of Na weights $=23 kg$
So, volume of $6 \times 10^{6} Na$ atoms $=\frac{23}{0.97} m^{3}$.
Volume occupied by one $Na$ atom $=\frac{23}{0.97 \times(6 \times 10^{26})}=3.95 \times 10^{-26} m^{3}$
Number of $Na$ atoms in target $({ }^{n} Na)$
$$ =\frac{10^{-7}}{3.95 \times 10^{-26}}=2.53 \times 10^{18} $$
Let $n$ be the number of photons falling per second on the target.
Energy of each photon $=h c / \lambda$
Total energy falling per second on target $=\frac{n h c}{\lambda}=I A$
$$ \begin{aligned} \therefore & n & =\frac{I A \lambda}{h c} \\ \Rightarrow & & =\frac{100 \times 10^{-4} \times(660 \times 10^{-9})}{(6.62 \times 10^{-34}) \times(3 \times 10^{8})}=3.3 \times 10^{16} \end{aligned} $$
Let $P$ be the probability of emission per atom per photon.
The number of photoelectrons emitted per second
$$ \begin{aligned} N & =P \times n \times({ }^{n} Na) \\ & =P \times(3.3 \times 10^{16}) \times(2.53 \times 10^{18}) \end{aligned} $$
Now, according to question,
$$ i=100 \mu A=100 \times 10^{-6}=10^{-4} A \text {. } $$
Current,
$$ \begin{aligned} i & =N e \\ 10^{-4} & =P \times(3.3 \times 10^{16}) \times(2.53 \times 10^{18}) \times(1.6 \times 10^{-19}) \\ P & =\frac{10^{-4}}{(3.3 \times 10^{16}) \times(2.53 \times 10^{18}) \times(1.6 \times 10^{-19})} \\ & =7.48 \times 10^{-21} \end{aligned} $$
$$ \begin{matrix} \therefore & 10^{-4}=P \times(3.3 \times 10^{16}) \times(2.53 \times 10^{18}) \times(1.6 \times 10^{-19}) \\ \Rightarrow & P=c \end{matrix} $$
Thus, the probability of emission by a single photon on a single atom is very much less than 1. It is due to this reason, the absorption of two photons by an atom is negligible.
26. Consider an electron in front of metallic surface at a distance $d$ (treated as an infinite plane surface). Assume the force of attraction by the plate is given as $\frac{1}{4} \frac{q^{2}}{4 \pi \varepsilon_0 d^{2}}$. Calculate work in taking the charge to an infinite distance from the plate. Taking $d=0.1 nm$, find the work done in electron volts.
Show Answer
Thinking Process
$$ \text { Work done by an external agency }=+\frac{1}{4 \pi \varepsilon_0} \cdot \frac{1}{4} \int_0^{\infty} \frac{q^{2}}{x^{2}} d x $$
Answer
According to question, consider the figure given below From figure, $d=0.1 nm=10^{-10} m$,
$$ F=\frac{q^{2}}{4 \times 4 \pi \varepsilon_0 d^{2}} $$
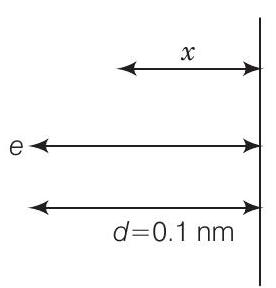
Let the electron be at distance $x$ from metallic surface. Then, force of attraction on it is
$$ F_{x}=\frac{q^{2}}{4 \times 4 \pi \varepsilon_0 x^{2}} $$
Work done by external agency in taking the electron from distance $d$ to infinity is
$$ \begin{aligned} W & =\int_1^{\infty} F_{x} d x=\int_1^{\infty} \frac{q^{2} d x}{4 \times 4 \pi \varepsilon_0} \frac{1}{x^{2}} \\ & =\frac{q^{2}}{4 \times 4 \pi \varepsilon_0} \frac{1}{d} \\ & =\frac{(1.6 \times 10^{-19})^{2} \times 9 \times 10^{9}}{4 \times 10^{-10}} J \\ & =\frac{(1.6 \times 10^{-19})^{2} \times(9 \times 10^{9})}{(4 \times 10^{-10}) \times(1.6 \times 10^{-19})} eV=3.6 eV \end{aligned} $$
27. A student performs an experiment on photoelectric effect, using two materials $A$ and $B$. A plot of $V_{\text {stop }}$ versus $v$ is given in figure.
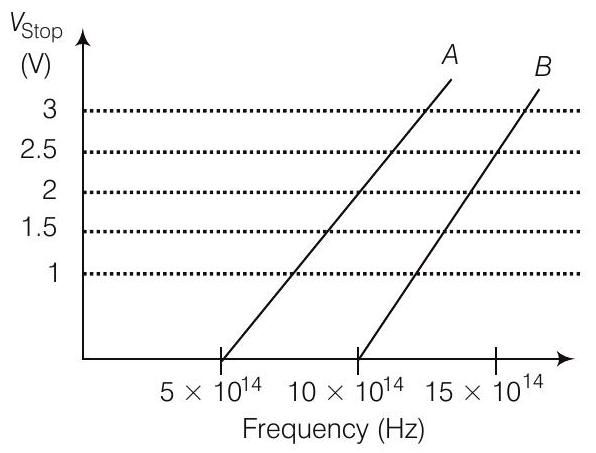
(i) Which material $A$ or $B$ has a higher work function?
(ii) Given the electric charge of an electron $=1.6 \times 10^{-19} C$, find the value of $h$ obtained from the experiment for both $A$ and $B$.
Comment on whether it is consistent with Einstein’s theory.
Show Answer
Answer
(i) Given, thresholed frequency of $A$ is given by $\nu_{O A}=5 \times 10^{14} Hz$ and For $B$,
$$ \nu_{O B}=10 \times 10^{14} Hz $$
We know that
Work function,
$$ \phi=h v_0 \text { or } \phi_0 \propto v_0 $$
$\Rightarrow$
$$ \begin{aligned} \phi_0 & \propto \nu_0 \\ \frac{\phi_{D A}}{\phi_{O B}} & =\frac{5 \times 10^{14}}{10 \times 10^{14}}<1 \\ \phi_{D A} & <\phi_{O B} \end{aligned} $$
So,
$\Rightarrow$
Thus, work function of $B$ is higher than $A$.
(ii) For metal $A$, slope $=\frac{h}{e}=\frac{2}{(10-5) 10^{14}}$
or
$$ \begin{aligned} h & =\frac{2 e}{5 \times 10^{14}}=\frac{2 \times 1.6 \times 10^{-19}}{5 \times 10^{14}} \\ & =6.4 \times 10^{-34} Js \end{aligned} $$
For metal $B$, slope $=\frac{h}{e}=\frac{2.5}{(15-10) 10^{14}}$
or
$$ \begin{aligned} h & =\frac{2.5 \times e}{5 \times 10^{14}}=\frac{2.5 \times 1.6 \times 10^{-19}}{5 \times 10^{14}} \\ & =8 \times 10^{-34} Js \end{aligned} $$
Since, the value of $h$ from experiment for metals $A$ and $B$ is different. Hence, experiment is not consistent with theory.
28. A particle $A$ with a mass $m_{A}$ is moving with a velocity $v$ and hits a particle $B$ (mass $m_{B}$ ) at rest (one dimensional motion). Find the change in the de-Broglie wavelength of the particle $A$. Treat the collision as elastic.
Show Answer
Answer
As collision is elastic, hence laws of conservation of momentum and kinetic energy are obeyed.
According to law of conservation of momentum,
$\Rightarrow$
$$ \begin{aligned} m_{A} v+m_{B} 0 & =m_{A} v_1+m_{B} v_2 \\ m_{A}(v-v_1) & =m_{B} v_2 \end{aligned} $$
According to law of conservation of kinetic energy,
$$ \begin{matrix} \Rightarrow \frac{1}{2} m_{A} v^{2} =\frac{1}{2} m_{A} v_1^{2}+\frac{1}{2} m_{B} v_2^{2} \\ \Rightarrow m_{A}(v-v_1^{2}) =m_{B} v_2^{2} \\ \Rightarrow m_{A}(v-v_1)(v+v_1) =m_{B} v_2^{2} \end{matrix} $$
Dividing E(ii) by Eq. (i),
we get, $\quad v+v_1=v_2$ or $v=v_2-v_1$
Solving Eqs. (i) and (iii), we get
$$ \begin{aligned} v_1 & =\frac{m_{A}-m_{B}}{m_{A}+m_{B}} \quad v \text { and } v_2=\frac{2 m_{A}}{m_{A}+m_{B}} v \\ \lambda_{\text {initial }} & =\frac{h}{m_{A} v} \\ \lambda_{\text {final }} & =\frac{h}{m_{A} v_1}=\frac{h(m_{A}+m_{B})}{m_{A}(m_{A}-m_{B}) v} \\ \Delta \lambda & =\lambda_{\text {final }}-\lambda_{\text {initial }}=\frac{h}{m_{A} v} \frac{m_{A}+m_{B}}{m_{A}-m_{B}}-1 \end{aligned} $$
29. Consider a $20 W$ bulb emitting light of wavelength $5000 \AA$ and shining on a metal surface kept at a distance $2 m$. Assume that the metal surface has work function of $2 eV$ and that each atom on the metal surface can be treated as a circular disk of radius $1.5 \AA$.
(i) Estimate number of photons emitted by the bulb per second.
[Assume no other losses]
(ii) Will there be photoelectric emission?
(iii) How much time would be required by the atomic disk to receive energy equal to work function $(2 eV)$ ?
(iv) How many photons would atomic disk receive within time duration calculated in (iii) above?
(v) Can you explain how photoelectric effect was observed instantaneously?
Show Answer
Answer
Given, $P=20 W, \lambda=5000 \AA=5000 \times 10^{-10} m$
$$ d=2 m, \phi_0=2 eV, r=1.5 A=1.5 \times 10^{-10} m $$
(i) Number of photon emitted by bulb per second is $n^{\prime}=\frac{p}{h c / \lambda}=\frac{p \lambda}{h c}$
$\Rightarrow$
$$ \begin{aligned} & =\frac{20 \times(5000 \times 10^{-10})}{(6.62 \times 10^{-34}) \times(3 \times 10^{8})} \\ & =5 \times 10^{19} s^{-1} \end{aligned} $$
(ii) Energy of the incident photon $=\frac{h c}{\lambda}=\frac{(6.62 \times 10^{-34})(3 \times 10^{8})}{5000 \times 10^{-10} \times 1.6 \times 10^{-19}}$
$$ =2.48 eV $$
As this energy is greater than $2 eV$ (i.e., work function of metal surface), hence photoelectric emission takes place.
(iii) Let $\Delta t$ be the time spent in getting the energy $\phi=$ (work function of metal).
Consider the figure,
$$ \Rightarrow \quad \begin{aligned} \frac{P}{4 \pi d^{2}} \times \pi r^{2} \Delta t & =\phi_0 \\ \Delta t & =\frac{4 \phi_0 d^{2}}{P r^{2}} \\ & =\frac{4 \times(2 \times 1.6 \times 10^{-19}) \times 2^{2}}{20 \times(1.5 \times 10^{-10})^{2}} \approx 28.4 s \end{aligned} $$
(iv) Number of photons received by atomic disc in time $\Delta t$ is
$$ \begin{aligned} N & =\frac{n^{\prime} \times \pi^{2}}{4 \pi d^{2}} \times \Delta t \\ & =\frac{n^{\prime} r^{2} \Delta t}{4 d^{2}} \\ & =\frac{(5 \times 10^{19}) \times(1.5 \times 10^{-10})^{2} \times 28.4}{4 \times(2)^{2}} \approx 2 \end{aligned} $$
(v) As time of emission of electrons is $11.04 s$.
Hence, the photoelectric emission is not instantaneous in this problem.
In photoelectric emission, there is an collision between incident photon and free electron of the metal surface, which lasts for very very short interval of time $(\approx 10^{-9} s)$, hence we say photoelectric emission is instantaneous










