Unit 8 The D And F Block Elements
The $d$-block of the periodic table contains the elements of the groups 3-12 in which the $d$ orbitals are progressively filled in each of the four long periods. The $f$-block consists of elements in which $4 f$ and $5 f$ orbitals are progressively filled. They are placed in a separate panel at the bottom of the periodic table. The names transition metals and inner transition metals are often used to refer to the elements of $d$-and $f$-blocks respectively.
There are mainly four series of the transition metals, $3 d$ series ( $\mathrm{Sc}$ to $\mathrm{Zn}$ ), $4 d$ series ( $\mathrm{Y}$ to $\mathrm{Cd}$ ), $5 d$ series (La and $\mathrm{Hf}$ to $\mathrm{Hg}$ ) and $6 d$ series which has $\mathrm{Ac}$ and elements from $\mathrm{Rf}$ to $\mathrm{Cn}$. The two series of the inner transition metals; $4 f(\mathrm{Ce}$ to $\mathrm{Lu})$ and $5 f$ (Th to $\mathrm{Lr}$ ) are known as lanthanoids and actinoids respectively.
Originally the name transition metals was derived from the fact that their chemical properties were transitional between those of $s$ and $p$-block elements. Now according to IUPAC, transition metals are defined as metals which have incomplete $d$ subshell either in neutral atom or in their ions. Zinc, cadmium and mercury of group 12 have full $d^{10}$ configuration in their ground state as well as in their common oxidation states and hence, are not regarded as transition metals. However, being the end members of the $3 d, 4 d$ and $5 d$ transition series, respectively, their chemistry is studied along with the chemistry of the transition metals.
The presence of partly filled d or f orbitals in their atoms makes transition elements different from that of the non-transition elements. Hence, transition elements and their compounds are studied separately. However, the usual theory of valence as applicable to the nontransition elements can be applied successfully to the transition elements also.
Various precious metals such as silver, gold and platinum and industrially important metals like iron, copper and titanium belong to the transition metals series. In this Unit, we shall first deal with the electronic configuration, occurrence and general characteristics of transition elements with special emphasis on the trends in the properties of the first row (3d) transition metals along with the preparation and properties of some important compounds. This will be followed by consideration of certain general aspects such as electronic configurations, oxidation states and chemical reactivity of the inner transition metals.
8.1 Position in the Periodic Table
The $d$-block occupies the large middle section of the periodic table flanked between $s$ - and $p$-blocks in the periodic table. The $d$-orbitals of the penultimate energy level of atoms receive electrons giving rise to four rows of the transition metals, i.e., $3 d, 4 d, 5 d$ and $6 d$. All these series of transition elements are shown in Table 8.1.
8.2 Electronic Configurations of the d-Block Elements
In general the electronic configuration of outer orbitals of these elements is $(n-1) d^{1-10} n s^{1-2}$ except for Pd where its electronic configuration is $4 d^{10} 5 s^{0}$. The ( $n-1$ ) stands for the inner $d$ orbitals which may have one to ten electrons and the outermost ns orbital may have one or two electrons. However, this generalisation has several exceptions because of very little energy difference between (n-1)d and ns orbitals. Furthermore, half and completely filled sets of orbitals are relatively more stable. A consequence of this factor is reflected in the electronic configurations of $\mathrm{Cr}$ and $\mathrm{Cu}$ in the $3 d$ series. For example, consider the case of $\mathrm{Cr}$, which has $3 d^{5} 4 s^{1}$ configuration instead of $3 d^{4} 4 s^{2}$; the energy gap between the two sets ( $3 d$ and $4 s$ ) of orbitals is small enough to prevent electron entering the $3 d$ orbitals. Similarly in case of $\mathrm{Cu}$, the configuration is $3 d^{10} 4 s^{1}$ and not $3 d^{9} 4 s^{2}$. The ground state electronic configurations of the outer orbitals of transition elements are given in Table 8.1.
Table 8.1: Electronic Configurations of outer orbitals of the Transition Elements (ground state)
| 1st Series | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| $\mathrm{Sc}$ | $\mathrm{Ti}$ | $\mathrm{V}$ | $\mathrm{Cr}$ | $\mathrm{Mn}$ | $\mathrm{Fe}$ | $\mathrm{Co}$ | $\mathrm{Ni}$ | $\mathrm{Cu}$ | $\mathrm{Zn}$ | |
| $Z$ | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| $4 s$ | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 1 | 2 |
| $3 d$ | 1 | 2 | 3 | 5 | 5 | 6 | 7 | 8 | 10 | 10 |
| 2nd Series | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| $\mathrm{Y}$ | $\mathrm{Zr}$ | $\mathrm{Nb}$ | $\mathrm{Mo}$ | $\mathrm{Tc}$ | $\mathrm{Ru}$ | $\mathrm{Rh}$ | $\mathrm{Pd}$ | $\mathrm{Ag}$ | $\mathrm{Cd}$ | |
| $Z$ | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
| $5 s$ | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 2 |
| $4 d$ | 1 | 2 | 4 | 5 | 6 | 7 | 8 | 10 | 10 | 10 |
| 3rd Series | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| $\mathrm{La}$ | $\mathrm{Hf}$ | $\mathrm{Ta}$ | $\mathrm{W}$ | $\mathrm{Re}$ | $\mathrm{Os}$ | $\mathrm{Ir}$ | $\mathrm{Pt}$ | $\mathrm{Au}$ | $\mathrm{Hg}$ | |
| $Z$ | 57 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| $6 d$ | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 2 |
| $5 d$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 10 |
| 4th Series | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| $\mathrm{Ac}$ | $\mathrm{Rf}$ | $\mathrm{Db}$ | $\mathrm{Sg}$ | $\mathrm{Bh}$ | $\mathrm{Hs}$ | $\mathrm{Mt}$ | $\mathrm{Ds}$ | $\mathrm{Rg}$ | $\mathrm{Cn}$ | |
| $Z$ | 89 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 |
| $7 s$ | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 |
| $6 d$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 10 | 10 |
The electronic configurations of outer orbitals of $\mathrm{Zn}, \mathrm{Cd}, \mathrm{Hg}$ and $\mathrm{Cn}$ are represented by the general formula $(n-1) d^{10} n s^{2}$. The orbitals in these elements are completely filled in the ground state as well as in their common oxidation states. Therefore, they are not regarded as transition elements. The $d$ orbitals of the transition elements protrude to the periphery of an atom more than the other orbitals (i.e., $s$ and $p$ ), hence, they are more influenced by the surroundings as well as affect the atoms or molecules surrounding them. In some respects, ions of a given $d^{\mathrm{n}}$ configuration ( $n=1-9$ ) have similar magnetic and electronic properties. With partly filled $d$ orbitals these elements exhibit certain characteristic properties such as display of a variety of oxidation states, formation of coloured ions and entering into complex formation with a variety of ligands.
The transition metals and their compounds also exhibit catalytic property and paramagnetic behaviour. All these characteristics have been discussed in detail later in this Unit.
There are greater similarities in the properties of the transition elements of a horizontal row in contrast to the non-transition elements. However, some group similarities also exist. We shall first study the general characteristics and their trends in the horizontal rows (particularly $3 d$ row) and then consider some group similarities.
Intext Question
8.1 Silver atom has completely filled $d$ orbitals $\left(4 d^{10}\right)$ in its ground state. How can you say that it is a transition element?
Show Answer
Answer
Ag has a completely filled $4 d$ orbital $\left(4 d^{10} 5 s^{1}\right)$ in its ground state. Now, silver displays two oxidation states (+1 and +2 ). In the +1 oxidation state, an electron is removed from the $s$-orboital. However, in the +2 oxidation state, an electron is removed from the $d$-orbital. Thus, the $d$-orbital now becomes incomplete $\left(4 d^{9}\right)$. Hence, it is a transition element.
8.3 General Properties of the Transition Elements (d-Block)
We will discuss the properties of elements of first transition series only in the following sections.
8.3.1 Physical Properties
Nearly all the transition elements display typical metallic properties such as high tensile strength, ductility, malleability, high thermal and electrical conductivity and metallic lustre. With the exceptions of $\mathrm{Zn}$, $\mathrm{Cd}, \mathrm{Hg}$ and $\mathrm{Mn}$, they have one or more typical metallic structures at normal temperatures.
Lattice Structures of Transition Metals
| Sc | Ti | V | Cr | Mn | Fe | Co | Ni | Cu | Zn |
|---|---|---|---|---|---|---|---|---|---|
| $hcp$ | $hcp$ | $bcc$ | $bcc$ | $X$ | $bcc$ | $ccp$ | $ccp$ | $ccp$ | $X$ |
| $(bcc)$ | $(bcc)$ | $(bcc, ccp)$ | $(hcp)$ | $(hcp)$ | $(hcp)$ | ||||
| $\mathbf{Y}$ | $\mathbf{Z r}$ | $\mathbf{N b}$ | $\mathbf{M o}$ | $\mathbf{T c}$ | $\mathbf{R u}$ | $\mathbf{R h}$ | $\mathbf{P d}$ | $\mathbf{A g}$ | $\mathbf{C d}$ |
| $hcp$ | $hcp$ | $bcc$ | $bcc$ | $hcp$ | $hcp$ | $ccp$ | $ccp$ | $ccp$ | $X$ |
| $(bcc)$ | $(bcc)$ | $(hcp)$ | |||||||
| $\mathbf{L a}$ | $\mathbf{H f}$ | $\mathbf{T a}$ | $\mathbf{W}$ | $\mathbf{R e}$ | $\mathbf{O s}$ | $\mathbf{I r}$ | $\mathbf{P t}$ | $\mathbf{A u}$ | $\mathbf{H g}$ |
| $hcp$ | $hcp$ | $bcc$ | $bcc$ | $hcp$ | $hcp$ | $ccp$ | $ccp$ | $ccp$ | $X$ |
| $(ccp,bcc)$ | $(bcc)$ |
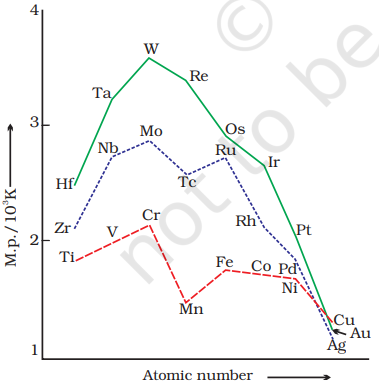
Fig. 8.1: Trends in melting points of transition elements
The transition metals (with the exception of $\mathrm{Zn}, \mathrm{Cd}$ and $\mathrm{Hg}$ ) are very hard and have low volatility. Their melting and boiling points are high. Fig. 8.1 depicts the melting points of transition metals belonging to $3 d, 4 d$ and $5 d$ series. The high melting points of these metals are attributed to the involvement of greater number of electrons from (n-1)d in addition to the ns electrons in the interatomic metallic bonding. In any row the melting points of these metals rise to a maximum at $d^{5}$ except for anomalous values of $\mathrm{Mn}$ and $\mathrm{Tc}$ and fall regularly as the atomic number increases. They have high enthalpies of atomisation which are shown in Fig. 8.2. The maxima at about the middle of each series indicate that one unpaired electron per $d$ orbital is particularly favourable for strong interatomic interaction. In general, greater the number of valence electrons, stronger is the resultant bonding. Since the enthalpy of atomisation is an important factor in determining the standard electrode potential of a metal, metals with very high enthalpy of atomisation (i.e., very high boiling point) tend to be noble in their reactions (see later for electrode potentials).
Another generalisation that may be drawn from Fig. 8.2 is that the metals of the second and third series have greater enthalpies of atomisation than the corresponding elements of the first series; this is an important factor in accounting for the occurrence of much more frequent metal - metal bonding in compounds of the heavy transition metals.
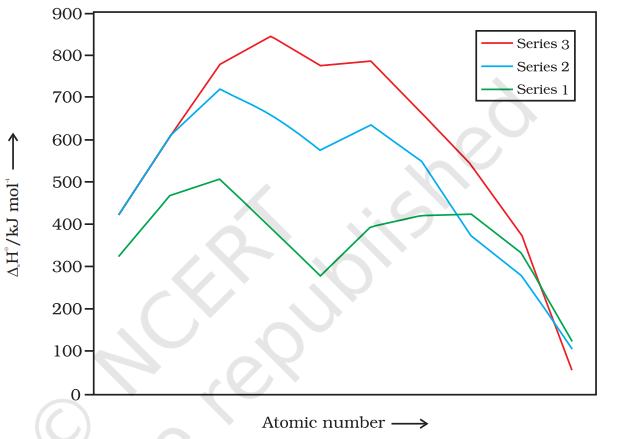
Fig. 8.2 Trends in enthalpies of atomisation of transition elements
8.3.2 Variation in Atomic and Ionic Sizes of Transition Metals
In general, ions of the same charge in a given series show progressive decrease in radius with increasing atomic number. This is because the new electron enters a $d$ orbital each time the nuclear charge increases by unity. It may be recalled that the shielding effect of a $d$ electron is not that effective, hence the net electrostatic attraction between the nuclear charge and the outermost electron increases and the ionic radius decreases. The same trend is observed in the atomic radii of a given series. However, the variation within a series is quite small. An interesting point emerges when atomic sizes of one series are compared with those of the corresponding elements in the other series. The curves in Fig. 8.3 show an increase from the first (3d) to the second (4d) series of the elements but the radii of the third $(5 d)$ series are virtually the same as those of the corresponding members of the second series. This phenomenon is associated with the intervention of the $4 f$ orbitals which must be filled before the $5 d$ series of elements begin. The filling of $4 f$ before $5 d$ orbital results in a regular decrease in atomic radii called Lanthanoid contraction which essentially compensates for the expected increase in atomic size with increasing atomic number. The net result of the lanthanoid contraction is that the second and the third $d$ series exhibit similar radii (e.g., Zr 160 pm, Hf $159 \mathrm{pm}$ ) and have very similar physical and chemical properties much more than that expected on the basis of usual family relationship.
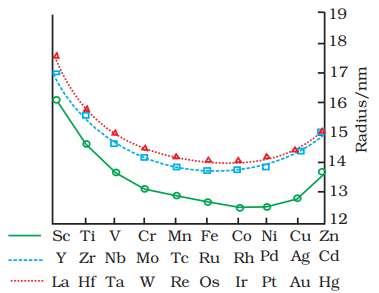
Fig. 8.3: Trends in atomic radii of transition elements
The factor responsible for the lanthanoid contraction is somewhat similar to that observed in an ordinary transition series and is attributed to similar cause, i.e., the imperfect shielding of one electron by another in the same set of orbitals. However, the shielding of one $4 f$ electron by another is less than that of one $d$ electron by another, and as the nuclear charge increases along the series, there is fairly regular decrease in the size of the entire $4 f^{n}$ orbitals.
The decrease in metallic radius coupled with increase in atomic mass results in a general increase in the density of these elements. Thus, from titanium $(Z=22)$ to copper $(Z=29)$ the significant increase in the density may be noted (Table 8.2).
Table 8.2: Electronic Configurations and some other Properties of the First Series of Transition Elements
| Element | Sc | $\mathbf{T i}$ | $\mathbf{V}$ | $\mathrm{Cr}$ | $\mathbf{M n}$ | $\mathrm{Fe}$ | Co | Ni | $\mathrm{Cu}$ | $\mathbf{Z n}$ | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Atomic number Electronic configuration |
21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| $\mathrm{M}$ | $3 d^1 4 s^2$ | $3 d^2 4 s^2$ | $3 d^3 4 s^2$ | $3 d^5 4 s^1$ | $3 d^5 4 s^2$ | $3 d^8 4 s^2$ | $3 d^7 4 s^2$ | $3 d^8 4 s^2$ | $3 d^{10} 4 s^1$ | $3 d^{10} 4 s^2$ | |
| $\mathrm{M}^{+}$ | $3 d^1 4 s^1$ | $3 d^2 4 s^1$ | $3 d^3 4 s^1$ | $3 d^5$ | $3 d^5 4 s^1$ | $3 d^6 4 s^1$ | $3 d^7 4 s^1$ | $3 d^8 4 s^1$ | $3 d^{10}$ | $3 d^{10} 4 s^1$ | |
| $\mathrm{M}^{2+}$ | $3 d^1$ | $3 d^2$ | $3 d^3$ | $3 d^4$ | $3 d^5$ | $3 d^6$ | $3 d^7$ | $3 d^8$ | $3 d^2$ | $3 d^{10}$ | |
| $\mathrm{M}^{3+}$ | $[A r]$ | $3 d^1$ | $3 d^2$ | $3 d^3$ | $3 d^4$ | $3 d^5$ | $3 d^6$ | $3 d^7$ | - | - | |
| Enthalpy of ato isation, $\Delta_a H^{\circ} / \mathbf{k} \mathbf{J}$ $\mathrm{mol}^{-1}$ | |||||||||||
| 326 | 473 | 515 | 397 | 281 | 416 | 425 | 430 | 339 | 126 | ||
| Ionisation enth $\mathrm{py} / \Delta_i H^{\circ} / \mathbf{1}$ $\mathbf{k} \mathbf{J} \mathrm{mol}^{-1}$ | |||||||||||
| $\Delta_2 H^{\circ}$ | I | 631 | 656 | 650 | 653 | 717 | 762 | 758 | 736 | 745 | 906 |
| $\Delta_1 H^{\circ}$ | II | 1235 | 1309 | 1414 | 1592 | 1509 | 1561 | 1644 | 1752 | 1958 | 1734 |
| $\Delta_i H^{\circ}$ | III | 2393 | 2657 | 2833 | 2990 | 3260 | 2962 | 3243 | 3402 | 3556 | 3837 |
| Metallic/ionic | $\mathrm{M}$ | 164 | 147 | 135 | 129 | 137 | 126 | 125 | 125 | 128 | 137 |
| radii/pm | $\mathrm{M}^{2+}$ | - | - | 79 | 82 | 82 | 77 | 74 | 70 | 73 | 75 |
| $\mathrm{M}^{3+}$ | 73 | 67 | 64 | 62 | 65 | 65 | 61 | 60 | - | - | |
| Standard | |||||||||||
| electrode | $\mathrm{M}^{2+} / \mathrm{M}$ | - | -1.63 | -1.18 | -0.90 | -1.18 | -0.44 | -0.28 | -0.25 | +0.34 | -0.76 |
| potential $E^{\circ} / \mathrm{V}$ | $\mathrm{M}^{3+} / \mathrm{M}^{2+}$ | - | -0.37 | -0.26 | -0.41 | +1.57 | +0.77 | +1.97 | - | - | - |
| Density/g $\mathrm{cm}^{-3}$ | 3.43 | 4.1 | 6.07 | 7.19 | 7.21 | 7.8 | 8.7 | 8.9 | 8.9 | 7.1 |
Example 8.2 Why do the transition elements exhibit higher enthalpies of atomisation?
Solution Because of large number of unpaired electrons in their atoms they have stronger interatomic interaction and hence stronger bonding between atoms resulting in higher enthalpies of atomisation.
Intext Question
8.2 In the series $\mathrm{Sc}(Z=21)$ to $\mathrm{Zn}(Z=30)$, the enthalpy of atomization of zinc is the lowest, i.e., $126 \mathrm{~kJ} \mathrm{~mol}^{-1}$. Why?
Show Answer
Answer
The extent of metallic bonding an element undergoes decides the enthalpy of atomization. The more extensive the metallic bonding of an element, the more will be its enthalpy of atomization. In all transition metals (except Zn, electronic configuration: $3 d^{10} 4 s^{2}$ ), there are some unpaired electrons that account for their stronger metallic bonding. Due to the absence of these unpaired electrons, the inter-atomic electronic bonding is the weakest in $\mathrm{Zn}$ and as a result, it has the least enthalpy of atomization.
8.3.3 Ionisation Enthalpies
There is an increase in ionisation enthalpy along each series of the transition elements from left to right due to an increase in nuclear charge which accompanies the filling of the inner d orbitals. Table 8.2 gives the values of the first three ionisation enthalpies of the first series of transition elements. These values show that the successive enthalpies of these elements do not increase as steeply as in the case of non-transition elements. The variation in ionisation enthalpy along a series of transition elements is much less in comparison to the variation along a period of non-transition elements. The first ionisation enthalpy, in general, increases, but the magnitude of the increase in the second and third ionisation enthalpies for the successive elements, is much higher along a series.
The irregular trend in the first ionisation enthalpy of the metals of $3 d$ series, though of little chemical significance, can be accounted for by considering that the removal of one electron alters the relative energies of $4 s$ and $3 d$ orbitals. You have learnt that when $d$-block elements form ions, $n s$ electrons are lost before $(n-1) d$ electrons. As we move along the period in $3 d$ series, we see that nuclear charge increases from scandium to zinc but electrons are added to the orbital of inner subshell, i.e., $3 d$ orbitals. These $3 d$ electrons shield the $4 s$ electrons from the increasing nuclear charge somewhat more effectively than the outer shell electrons can shield one another. Therefore, the atomic radii decrease less rapidly. Thus, ionization energies increase only slightly along the $3 d$ series. The doubly or more highly charged ions have $d^{\mathrm{n}}$ configurations with no $4 s$ electrons. A general trend of increasing values of second ionisation enthalpy is expected as the effective nuclear charge increases because one $d$ electron does not shield another electron from the influence of nuclear charge because $d$-orbitals differ in direction. However, the trend of steady increase in second and third ionisation enthalpy breaks for the formation of $\mathrm{Mn}^{2+}$ and $\mathrm{Fe}^{3+}$ respectively. In both the cases, ions have $d^{5}$ configuration. Similar breaks occur at corresponding elements in the later transition series.
The interpretation of variation in ionisation enthalpy for an electronic configuration $d^{n}$ is as follows:
The three terms responsible for the value of ionisation enthalpy are attraction of each electron towards nucleus, repulsion between the electrons and the exchange energy. Exchange energy is responsible for the stabilisation of energy state. Exchange energy is approximately proportional to the total number of possible pairs of parallel spins in the degenerate orbitals. When several electrons occupy a set of degenerate orbitals, the lowest energy state corresponds to the maximum possible extent of single occupation of orbital and parallel spins (Hunds rule). The loss of exchange energy increases the stability. As the stability increases, the ionisation becomes more difficult. There is no loss of exchange energy at $d^{6}$ configuration. $\mathrm{Mn}^{+}$has $3 d^{5} 4 s^{1}$ configuration and configuration of $\mathrm{Cr}^{+}$is $d^{5}$, therefore, ionisation enthalpy of $\mathrm{Mn}^{+}$is lower than $\mathrm{Cr}^{+}$. In the same way, $\mathrm{Fe}^{2+}$ has $d^{6}$ configuration and $\mathrm{Mn}^{2+}$ has $3 d^{5}$ configuration. Hence, ionisation enthalpy of $\mathrm{Fe}^{2+}$ is lower than the $\mathrm{Mn}^{2+}$. In other words, we can say that the third ionisation enthalpy of $\mathrm{Fe}$ is lower than that of Mn.
The lowest common oxidation state of these metals is +2 . To form the $\mathrm{M}^{2+}$ ions from the gaseous atoms, the sum of the first and second ionisation enthalpy is required in addition to the enthalpy of atomisation. The dominant term is the second ionisation enthalpy which shows unusually high values for $\mathrm{Cr}$ and $\mathrm{Cu}$ where $\mathrm{M}^{+}$ions have the $d^{5}$ and $d^{10}$ configurations respectively. The value for $\mathrm{Zn}$ is correspondingly low as the ionisation causes the removal of one $4 s$ electron which results in the formation of stable $d^{10}$ configuration. The trend in the third ionisation enthalpies is not complicated by the $4 s$ orbital factor and shows the greater difficulty of removing an electron from the $d^{5}\left(\mathrm{Mn}^{2+}\right)$ and $d^{10}\left(\mathrm{Zn}^{2+}\right)$ ions. In general, the third ionisation enthalpies are quite high. Also the high values for third ionisation enthalpies of copper, nickel and zinc indicate why it is difficult to obtain oxidation state greater than two for these elements.
Although ionisation enthalpies give some guidance concerning the relative stabilities of oxidation states, this problem is very complex and not amenable to ready generalisation.
8.3.4 Oxidation States
One of the notable features of a transition elements is the great variety of oxidation states these may show in their compounds. Table 8.3 lists the common oxidation states of the first row transition elements.
Table 8.3: Oxidation States of the first row Transition Metal (the most common ones are in bold types)
| Sc | Ti | V | Cr | Mn | Fe | Co | Ni | Cu | Zn |
|---|---|---|---|---|---|---|---|---|---|
| +3 | +2 | +2 | +2 | +2 | +2 | +2 | +2 | +1 | $\mathbf{+ 2}$ |
| +3 | +3 | +3 | +3 | $\mathbf{+ 3}$ | $\mathbf{+ 3}$ | +3 | +2 | ||
| +4 | +4 | +4 | +4 | +4 | +4 | +4 | |||
| +5 | +5 | +5 | |||||||
| +6 | +6 | +6 | |||||||
| +7 |
The elements which give the greatest number of oxidation states occur in or near the middle of the series. Manganese, for example, exhibits all the oxidation states from +2 to +7 . The lesser number of oxidation states at the extreme ends stems from either too few electrons to lose or share ( $\mathrm{Sc}, \mathrm{Ti}$ ) or too many $d$ electrons (hence fewer orbitals available in which to share electrons with others) for higher valence $(\mathrm{Cu}, \mathrm{Zn})$. Thus, early in the series scandium(II) is virtually unknown and titanium (IV) is more stable than Ti(III) or Ti(II). At the other end, the only oxidation state of zinc is +2 (no $d$ electrons are involved). The maximum oxidation states of reasonable stability correspond in value to the sum of the $s$ and $d$ electrons upto manganese $\left(\mathrm{Ti}^{\mathrm{VV}} \mathrm{O_2}, \mathrm{~V}^{\mathrm{V}} \mathrm{O_2} ^{+}\right).$, $\mathrm{Cr}^{\mathrm{Vl}} \mathrm{O_4} ^{2-}, \mathrm{Mn}^{\mathrm{VII}} \mathrm{O_4}^-$ followed by a rather abrupt decrease in stability of higher oxidation states, so that the typical species to follow are $\mathrm{Fe}^{\mathrm{IIIIII}}$, $\mathrm{Co}^{\mathrm{II}, \mathrm{II}}, \mathrm{Ni}^{\mathrm{II}}, \mathrm{Cu}^{\mathrm{I}, \mathrm{II}}, \mathrm{Zn}^{\mathrm{II}}$.
The variability of oxidation states, a characteristic of transition elements, arises out of incomplete filling of $d$ orbitals in such a way that their oxidation states differ from each other by unity, e.g., $V^{\mathrm{II}}, V^{\mathrm{II}}$, $\mathrm{V}^{\mathrm{V}}, \mathrm{V}$. This is in contrast with the variability of oxidation states of non transition elements where oxidation states normally differ by a unit of two.
An interesting feature in the variability of oxidation states of the $d-$ block elements is noticed among the groups (groups 4 through 10). Although in the $p$-block the lower oxidation states are favoured by the heavier members (due to inert pair effect), the opposite is true in the groups of $d$-block. For example, in group 6, Mo(VI) and W(VI) are found to be more stable than $\mathrm{Cr}(\mathrm{VI})$. Thus $\mathrm{Cr}(\mathrm{VI})$ in the form of dichromate in acidic medium is a strong oxidising agent, whereas $\mathrm{MoO_3}$ and $\mathrm{WO_3}$ are not.
Low oxidation states are found when a complex compound has ligands capable of $\pi$-acceptor character in addition to the $\sigma$-bonding. For example, in $\mathrm{Ni}\mathrm{CO_4}$ and $\mathrm{Fe}\mathrm{CO_5}$, the oxidation state of nickel and iron is zero.
Example 8.3 Name a transition element which does not exhibit variable oxidation states.
Solution Scandium $(Z=21)$ does not exhibit variable oxidation states.
Intext Question
8.3 Which of the $3 d$ series of the transition metals exhibits the largest number of oxidation states and why?
Show Answer
Answer
$\mathrm{Mn}(\mathrm{Z}=25)=3 d^{5} 4 \mathrm{~s}^{2}$
Mn has the maximum number of unpaired electrons present in the $d$-subshell (5 electrons). Hence, Mn exhibits the largest number of oxidation states, ranging from +2 to +7 .
8.3.5 Trends in the M2+/M Standard Electrode Potentials
Table 8.4 contains the thermochemical parameters related to the transformation of the solid metal atoms to $\mathrm{M}^{2+}$ ions in solution and their standard electrode potentials. The observed values of $E^{\ominus}$ and those calculated using the data of Table 8.4 are compared in Fig. 8.4.
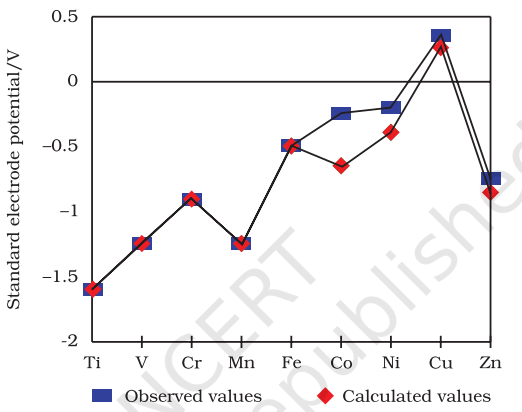
Fig. 8.4: Observed and calculated values for the standard electrode potentials
The unique behaviour of $\mathrm{Cu}$, having a positive $E^{\ominus}$, accounts for its inability to liberate $\mathrm{H_2}$ from acids. Only oxidising acids (nitric and hot concentrated sulphuric) react with $\mathrm{Cu}$, the acids being reduced. The high energy to transform $\mathrm{Cu}(\mathrm{s})$ to $\mathrm{Cu}^{2+}(\mathrm{aq})$ is not balanced by its hydration enthalpy. The general trend towards less negative $E^{\ominus}$ values across the series is related to the general increase in the sum of the first and second ionisation enthalpies. It is interesting to note that the value of $E^{\ominus}$ for Mn, $\mathrm{Ni}$ and $\mathrm{Zn}$ are more negative than expected from the trend.
Fig. 8.4: Observed and calculated values for the standard electrode potentials $\left(M^{2+} \rightarrow M^{\circ}\right)$ of the elements Ti to $\mathrm{Zn}$
| Element (M) | $\Delta_{\mathbf{a}} \boldsymbol{H}^{\circ}(\mathbf{M})$ | $\Delta_{\imath} \mathbf{H}_1^{\circ}$ | $\Delta_1 \mathbf{H}_2^{\circ}$ | $\Delta_{\text {hyd }} \mathbf{H}^0\left(\mathbf{M}^{2+}\right)$ | $\mathbf{E}^{\circ} / \mathbf{v}$ |
|---|---|---|---|---|---|
| $\mathrm{Ti}$ | 469 | 656 | 1309 | -1866 | -1.63 |
| $\mathrm{V}$ | 515 | 650 | 1414 | -1895 | -1.18 |
| $\mathrm{Cr}$ | 398 | 653 | 1592 | -1925 | -0.90 |
| $\mathrm{Mn}$ | 279 | 717 | 1509 | -1862 | -1.18 |
| $\mathrm{Fe}$ | 418 | 762 | 1561 | -1998 | -0.44 |
| Co | 427 | 758 | 1644 | -2079 | -0.28 |
| $\mathrm{Ni}$ | 431 | 736 | 1752 | -2121 | -0.25 |
| $\mathrm{Cu}$ | 339 | 745 | 1958 | -2121 | 0.34 |
| $\mathrm{Zn}$ | 130 | 906 | 1734 | -2059 | -0.76 |
Example 8.4 Why is $\mathrm{Cr}^{2+}$ reducing and $\mathrm{Mn}^{3+}$ oxidising when both have $d^{4}$ configuration?
Solution $\mathrm{Cr}^{2+}$ is reducing as its configuration changes from $d^{4}$ to $d^{3}$, the latter having a half-filled $t_{2 g}$ level (see Unit 9) . On the other hand, the change from $\mathrm{Mn}^{3+}$ to $\mathrm{Mn}^{2+}$ results in the half-filled $\left(d^{5}\right)$ configuration which has extra stability.
The stability of the half-filled $d$ sub-shell in $\mathrm{Mn}^{2+}$ and the completely filled $d^{10}$ configuration in $\mathrm{Zn}^{2+}$ are related to their $E^{\ominus}$ values, whereas $E^{\ominus}$ for Ni is related to the highest negative $\Delta_{\text {hyd }} H^{\ominus}$.
8.3.6 Trends in the M3+/M2+ Standard Electrode Potentials
An examination of the $E^{\ominus}\left(\mathrm{M}^{3+} / \mathrm{M}^{2+}\right)$ values (Table 8.2) shows the varying trends. The low value for $\mathrm{Sc}$ reflects the stability of $\mathrm{Sc}^{3+}$ which has a noble gas configuration. The highest value for $\mathrm{Zn}$ is due to the removal of an electron from the stable $d^{10}$ configuration of $\mathrm{Zn}^{2+}$. The comparatively high value for $\mathrm{Mn}$ shows that $\mathrm{Mn}^{2+}\left(d^{5}\right)$ is particularly stable, whereas comparatively low value for $\mathrm{Fe}$ shows the extra stability of $\mathrm{Fe}^{3+}\left(d^{5}\right)$. The comparatively low value for $\mathrm{V}$ is related to the stability of $\mathrm{V}^{2+}$ (half-filled $t_{2 \mathrm{~g}}$ level, Unit 9).
8.3.7 Trends in Stability of Higher Oxidation States
Table 8.5 shows the stable halides of the $3 d$ series of transition metals. The highest oxidation numbers are achieved in $\mathrm{TiX_4}$ (tetrahalides), $\mathrm{VF_5}$ and $\mathrm{CrF_6}$. The +7 state for $\mathrm{Mn}$ is not represented in simple halides but $\mathrm{MnO_3} \mathrm{~F}$ is known, and beyond $\mathrm{Mn}$ no metal has a trihalide except $\mathrm{FeX_3}$ and $\mathrm{CoF_3}$. The ability of fluorine to stabilise the highest oxidation state is due to either higher lattice energy as in the case of $\mathrm{CoF_3}$, or higher bond enthalpy terms for the higher covalent compounds, e.g., $\mathrm{VF_5}$ and $\mathrm{CrF_6}$.
Although $\mathrm{V}^{+5}$ is represented only by $\mathrm{VF_5}$, the other halides, however, undergo hydrolysis to give oxohalides, $\mathrm{VOX_3}$. Another feature of fluorides is their instability in the low oxidation states e.g., $\mathrm{VX_2}(\mathrm{X}=\mathrm{CI}, \mathrm{Br}$ or $\mathrm{I})$
Table 8.5: Formulas of Halides of 3d Metals

and the same applies to $\mathrm{CuX}$. On the other hand, all $\mathrm{Cu}^{\mathrm{II}}$ halides are known except the iodide. In this case, $\mathrm{Cu}^{2+}$ oxidises $\mathrm{I}^{-}$to $\mathrm{I_2}$ :
$$ 2 \mathrm{Cu}^{2+}+4 \mathrm{I}^{-} \rightarrow \mathrm{Cu_2} \mathrm{I_2}(\mathrm{~s})+\mathrm{I_2} $$
However, many copper (I) compounds are unstable in aqueous solution and undergo disproportionation.
$$ 2 \mathrm{Cu}^{+} \rightarrow \mathrm{Cu}^{2+}+\mathrm{Cu} $$
The stability of $\mathrm{Cu}^{2+}$ (aq) rather than $\mathrm{Cu}^{+}(\mathrm{aq})$ is due to the much more negative $\Delta_{\text {hyd }} \mathrm{H}^{\ominus}$ of $\mathrm{Cu}^{2+}$ (aq) than $\mathrm{Cu}^{+}$, which more than compensates for the second ionisation enthalpy of $\mathrm{Cu}$.
The ability of oxygen to stabilise the highest oxidation state is demonstrated in the oxides. The highest oxidation number in the oxides (Table 8.6) coincides with the group number and is attained in $\mathrm{Sc_2} \mathrm{O_3}$ to $\mathrm{Mn_2} \mathrm{O_7}$. Beyond Group 7, no higher oxides of $\mathrm{Fe}$ above $\mathrm{Fe_2} \mathrm{O_3}$, are known, although ferrates (VI) $\left(\mathrm{FeO_4}\right)^{2-}$, are formed in alkaline media but they readily decompose to $\mathrm{Fe_2} \mathrm{O_3}$ and $\mathrm{O_2}$. Besides the oxides, oxocations stabilise $\mathrm{V}^{\mathrm{v}}$ as $\mathrm{VO_2}^{+}, \mathrm{V}^{\mathrm{IV}}$ as $\mathrm{VO}^{2+}$ and $\mathrm{Ti}^{\mathrm{IV}}$ as $\mathrm{TiO}^{2+}$. The ability of oxygen to stabilise these high oxidation states exceeds that of fluorine. Thus the highest Mn fluoride is $\mathrm{MnF_4}$ whereas the highest oxide is $\mathrm{Mn_2} \mathrm{O_7}$. The ability of oxygen to form multiple bonds to metals explains its superiority. In the covalent oxide $\mathrm{Mn_2} \mathrm{O_7}$, each $\mathrm{Mn}$ is tetrahedrally surrounded by O’s including a Mn-O-Mn bridge. The tetrahedral $\left[\mathrm{MO_4}\right]^{\mathrm{n}-}$ ions are known for $\mathrm{V}^{\mathrm{V}}, \mathrm{Cr}^{\mathrm{V}}, \mathrm{Mn}^{\mathrm{v}}, \mathrm{Mn}^{\mathrm{V}}$ and $\mathrm{Mn}^{\mathrm{VII}}$.
Table 8.5: Formulas of Halides of 3d Metals
| Oxidation Number |
Groups | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| +7 | $\mathrm{Mn} _{2} \mathrm{O} _{7}$ | |||||||||
| +6 | $\mathrm{CrO} _{3}$ | |||||||||
| +5 | $\mathrm{~V} _{2} \mathrm{O} _{5}$ | |||||||||
| +4 | $\mathrm{TiO} _{2}$ | $\mathrm{~V} _{2} \mathrm{O} _{4}$ | $\mathrm{CrO} _{2}$ | $\mathrm{MnO} _{2}$ | ||||||
| +3 | $\mathrm{Sc} _{2} \mathrm{O} _{3}$ | $\mathrm{Ti} _{2} \mathrm{O} _{3}$ | $\mathrm{~V} _{2} \mathrm{O} _{3}$ | $\mathrm{Cr} _{2} \mathrm{O} _{3}$ | $\mathrm{Mn} _{2} \mathrm{O} _{3}$ | $\mathrm{Fe} _{2} \mathrm{O} _{3}$ | ||||
| $\mathrm{Mn} _{3} \mathrm{O} _{4}{ }^{\ast}$ | $\mathrm{Fe} _{3} \mathrm{O} _{4}{ }^{\ast}$ | $\mathrm{Co} _{3} \mathrm{O} _{4}{ }^{\ast}$ | ||||||||
| +2 | $\mathrm{TiO}$ | VO | $(\mathrm{CrO})$ | $\mathrm{MnO}$ | $\mathrm{FeO}$ | $\mathrm{CoO}$ | $\mathrm{NiO}$ | $\mathrm{CuO}$ | $\mathrm{ZnO}$ | |
| +1 | $\mathrm{Cu} _{2} \mathrm{O}$ |
Example 8.5 How would you account for the increasing oxidising power in the series $\mathrm{VO_2}^{+}<\mathrm{Cr_2} \mathrm{O_7}^{2-}<\mathrm{MnO_4}{ }^{-}$?
Solution This is due to the increasing stability of the lower species to which they are reduced.
Intext Question
8.5 How would you account for the irregular variation of ionisation enthalpies (first and second) in the first series of the transition elements?
Show Answer
Answer
Ionization enthalpies are found to increase in the given series due to a continuous filling of the inner $d$-orbitals. The irregular variations of ionization enthalpies can be attributed to the extra stability of configurations such as $d^{0}, d^{5}, d^{10}$. Since these states are exceptionally stable, their ionization enthalpies are very high.
In case of first ionization energy, $\mathrm{Cr}$ has low ionization energy. This is because after losing one electron, it attains the stable configuration $\left(3 d^{5}\right)$. On the other hand, $\mathrm{Zn}$ has exceptionally high first ionization energy as an electron has to be removed from stable and fully-filled orbitals $\left(3 d^{10} 4 s^{2}\right)$.
Second ionization energies are higher than the first since it becomes difficult to remove an electron when an electron has already been taken out. Also, elements like $\mathrm{Cr}$ and $\mathrm{Cu}$ have exceptionally high second ionization energies as after losing the first electron, they have attained the stable configuration $\left(\mathrm{Cr}^{+}: 3 d^{5}\right.$ and $\mathrm{Cu}^{+}: 3 d^{10}$ ). Hence, taking out one electron more from this stable configuration will require a lot of energy.
8.3.8 Chemical Reactivity and $\mathbf{E}^{\ominus}$ Values
Transition metals vary widely in their chemical reactivity. Many of them are sufficiently electropositive to dissolve in mineral acids, although a few are ‘noble’—that is, they are unaffected by single acids.
The metals of the first series with the exception of copper are relatively more reactive and are oxidised by $1 \mathrm{M} \mathrm{H}^{+}$, though the actual rate at which these metals react with oxidising agents like hydrogen ion $\left(\mathrm{H}^{+}\right)$is sometimes slow. For example, titanium and vanadium, in practice, are passive to dilute non oxidising acids at room temperature. The $E^{\ominus}$ values for $\mathrm{M}^{2+} / \mathrm{M}$ (Table 8.2) indicate a decreasing tendency to form divalent cations across the series. This general trend towards less negative $E^{\ominus}$ values is related to the increase in the sum of the first and second ionisation enthalpies. It is interesting to note that the $E^{\ominus}$ values for Mn, $\mathrm{Ni}$ and $\mathrm{Zn}$ are more negative than expected from the general trend. Whereas the stabilities of half-filled $d$ subshell $\left(d^{5}\right)$ in $\mathrm{Mn}^{2+}$ and completely filled $d$ subshell $\left(d^{10}\right)$ in zinc are related to their $E^{\mathrm{e}}$ values; for nickel, $E^{\oplus}$ value is related to the highest negative enthalpy of hydration.
An examination of the $E^{\ominus}$ values for the redox couple $\mathrm{M}^{3+} / \mathrm{M}^{2+}$ (Table 8.2) shows that $\mathrm{Mn}^{3+}$ and $\mathrm{Co}^{3+}$ ions are the strongest oxidising agents in aqueous solutions. The ions $\mathrm{Ti}^{2+}, \mathrm{V}^{2+}$ and $\mathrm{Cr}^{2+}$ are strong reducing agents and will liberate hydrogen from a dilute acid, e.g.,
$$ 2 \mathrm{Cr}^{2+}(\mathrm{aq})+2 \mathrm{H}^{+}(\mathrm{aq}) \rightarrow 2 \mathrm{Cr}^{3+}(\mathrm{aq})+\mathrm{H_2}(\mathrm{~g}) $$
Example 8.6 For the first row transition metals the $E^{\circ}$ values are:
| $\boldsymbol{E}^{\oplus}$ | $\mathrm{V}$ | $\mathrm{Cr}$ | $\mathrm{Mn}$ | $\mathrm{Fe}$ | $\mathrm{Co}$ | $\mathrm{Ni}$ | $\mathrm{Cu}$ |
|---|---|---|---|---|---|---|---|
| $\left(\mathrm{M}^{2+} / \mathrm{M}\right)$ | -1.18 | -0.91 | -1.18 | -0.44 | -0.28 | -0.25 | +0.34 |
Explain the irregularity in the above values.
Solution The $E^{\ominus}\left(\mathrm{M}^{2+} / \mathrm{M}\right)$ values are not regular which can be explained from the irregular variation of ionisation enthalpies $\left(\Delta_{\mathrm{i}} H_{1}+\Delta_{\mathrm{i}} H_{2}\right)$ and also the sublimation enthalpies which are relatively much less for manganese and vanadium.
Example 8.7 Why is the $E^{\ominus}$ value for the $\mathrm{Mn}^{3+} / \mathrm{Mn}^{2+}$ couple much more positive than that for $\mathrm{Cr}^{3+} / \mathrm{Cr}^{2+}$ or $\mathrm{Fe}^{3+} / \mathrm{Fe}^{2+}$ ? Explain.
Solution
Much larger third ionisation energy of Mn (where the required change is $d^{5}$ to $d^{4}$ ) is mainly responsible for this. This also explains why the +3 state of Mn is of little importance.
Intext Questions
8.6 Why is the highest oxidation state of a metal exhibited in its oxide or fluoride only?
Show Answer
Answer
Both oxide and fluoride ions are highly electronegative and have a very small size. Due to these properties, they are able to oxidize the metal to its highest oxidation state.
8.7 Which is a stronger reducing agent $\mathrm{Cr}^{2+}$ or $\mathrm{Fe}^{2+}$ and why?
Show Answer
Answer
Stronger reducing agent out of $\mathrm{Cr}^{2+}$ and $\mathrm{Fe}^{2+}$ Hence, $\mathrm{Cr}^{2+}$ can easily oxidize to $\mathrm{Cr}^{3+}$, but $\mathrm{Fe}^{2+}$ does not get oxidized to $\mathrm{Fe}^{3+}$ easily.
Therefore, $\mathrm{Cr}^{2+}$ is a better reducing agent that $\mathrm{Fe}^{3+}$.
8.3.9 Magnetic Properties
When a magnetic field is applied to substances, mainly two types of magnetic behaviour are observed: diamagnetism and paramagnetism (Unit 1). Diamagnetic substances are repelled by the applied field while the paramagnetic substances are attracted. Substances which are attracted very strongly are said to be ferromagnetic. In fact, ferromagnetism is an extreme form of paramagnetism. Many of the transition metal ions are paramagnetic.
Paramagnetism arises from the presence of unpaired electrons, each such electron having a magnetic moment associated with its spin angular momentum and orbital angular momentum. For the compounds of the first series of transition metals, the contribution of the orbital angular momentum is effectively quenched and hence is of no significance. For these, the magnetic moment is determined by the number of unpaired electrons and is calculated by using the ‘spin-only’ formula, i.e.,
$$ \mu=\sqrt{\mathrm{n}(\mathrm{n}+2)} $$
where $\mathrm{n}$ is the number of unpaired electrons and $\mu$ is the magnetic moment in units of Bohr magneton (BM). A single unpaired electron has a magnetic moment of 1.73 Bohr magnetons (BM).
The magnetic moment increases with the increasing number of unpaired electrons. Thus, the observed magnetic moment gives a useful indication about the number of unpaired electrons present in the atom, molecule or ion. The magnetic moments calculated from the ‘spin-only’ formula and those derived experimentally for some ions of the first row transition elements are given in Table 8.7. The experimental data are mainly for hydrated ions in solution or in the solid state.
Table 8.7: Calculated and Observed Magnetic Moments (BM)
| Ion | Configuration | Unpaired electron(s) |
Magnetic moment | |
|---|---|---|---|---|
| Calculated | Observed | |||
| $\mathrm{Sc}^{3+}$ | $3 d^0$ | 0 | 0 | 0 |
| $\mathrm{Ti}^{3+}$ | $3 d^1$ | 1 | 1.73 | 1.75 |
| $\mathrm{Tn}^{2+}$ | $3 d^2$ | 2 | 2.84 | 2.76 |
| $\mathrm{~V}^{2+}$ | $3 d^3$ | 3 | 3.87 | 3.86 |
| $\mathrm{Cr}^{2+}$ | $3 d^4$ | 4 | 4.90 | 4.80 |
| $\mathrm{Mn}^{2+}$ | $3 d^5$ | 5 | 5.92 | 5.96 |
| $\mathrm{Fe}^{2+}$ | $3 d^6$ | 4 | 4.90 | $5.3-5.5$ |
| $\mathrm{Co}^{2+}$ | $3 d^7$ | 3 | 3.87 | $4.4-5.2$ |
| $\mathrm{Ni}^{2+}$ | $3 d^8$ | 2 | 2.84 | $2.9-3,4$ |
| $\mathrm{Cu}^{2+}$ | $3 d^9$ | 1 | 1.73 | $1.8-2.2$ |
| $\mathrm{Zn}^{2+}$ | $3 d^10$ | 0 | 0 |
Example 8.8 Calculate the magnetic moment of a divalent ion in aqueous solution if its atomic number is 25.
Solution With atomic number 25 , the divalent ion in aqueous solution will have $d^5$ configuration (five unpaired electrons). The magnetic moment, $\mu$ is $ \mu=\sqrt{5(5+2)}=5.92 \mathrm{BM} $
Intext Question
8.8 Calculate the ‘spin only’ magnetic moment of $\mathrm{M}^{2+}{ _(a q)}$ ion $(Z=27)$.
Show Answer
Answer
Number of unpaired electrons
Given:
Atomic number $(Z)=27$
The valence electronic configuration of cobalt ( $\mathrm{Co}$ ) is $3 d^7, 4 s^2$.
$\mathrm{M}^{2+}(\mathrm{aq})$ ion means, it loses two electrons.
Hence, valence electronic configuration becomes $d^7$.
Now, Number of unpaired electrons $=3$
Spin only magnetic moment
We know that $\mu=\sqrt{n(n+2)}$
where $n=$ number of unpaired electrons
Putting $\mathrm{n}=3$
we get, $\mu=\sqrt{3(3+2)}=3.87 \mathrm{BM}$
8.3.10 Formation of Coloured Ions
When an electron from a lower energy d orbital is excited to a higher energy d orbital, the energy of excitation corresponds to the frequency of light absorbed (Unit 9). This frequency generally lies in the visible region. The colour observed corresponds to the complementary colour of the light absorbed. The frequency of the light absorbed is determined by the nature of the ligand. In aqueous solutions where water molecules are the ligands, the colours of the ions observed are listed in Table 8.8. A few coloured solutions of d–block elements are illustrated in Fig. 8.5.
Fig. 8.5: Colours of some of the first row transition metal ions in aqueous solutions. From left to right: $\mathrm{V}^{4+}, \mathrm{V}^{3+}, \mathrm{Mn}^{2+}$, $\mathrm{Fe}^{3+}, \mathrm{Co}^{2+}, \mathrm{Ni}^{2+}$ $\mathrm{Cu}^{2+}$.

Table 8.8: Colours of Some of the First Row (aquated) Transition Metal Ions
| Configuration | Example | Colour |
|---|---|---|
| $3 \mathrm{~d}^0$ | $\mathrm{Sc}^{3+}$ | colourless |
| $3 \mathrm{~d}^0$ | $\mathrm{Ti}^{4+}$ | colourless |
| $3 \mathrm{~d}^1$ | $\mathrm{Ti}^{3+}$ | purple |
| $3 \mathrm{~d}^1$ | $\mathrm{~V}^{3+}$ | blue |
| $3 \mathrm{~d}^{2+}$ | $\mathrm{V}^{3+}$ | green |
| $3 \mathrm{~d}^3$ | $\mathrm{~V}^{2+}$ | violet |
| $3 \mathrm{~d}^3$ | $\mathrm{Cr}^{3+}$ | violet |
| $3 \mathrm{~d}^4$ | $\mathrm{Mn}^{3+}$ | violet |
| $3 \mathrm{~d}^4$ | $\mathrm{Cr}^{2+}$ | blue |
| $3 \mathrm{~d}^5$ | $\mathrm{Mn}^{2+}$ | pink |
| $3 \mathrm{~d}^5$ | $\mathrm{Fe}^{3+}$ | yellow |
| $3 \mathrm{~d}^6$ | $\mathrm{Fe}^{2+}$ | green |
| $3 \mathrm{~d}^6 3 \mathrm{~d}^7$ | $\mathrm{Co}^{3+} \mathrm{Co}^{2+}$ | bluepink |
| $3 \mathrm{~d}^8$ | $\mathrm{Ni}^{2+}$ | green |
| $3 \mathrm{~d}^9$ | $\mathrm{Cu}^{2+}$ | blue |
| $3 \mathrm{~d}^{10}$ | $\mathrm{Zn}^{2^{2+}}$ | colourless |
8.3.11 Formation of Complex Compounds
Complex compounds are those in which the metal ions bind a number of anions or neutral molecules giving complex species with characteristic properties. A few examples are: $\left[\mathrm{Fe}\mathrm{CN}_6\right]^{3-},\left[\mathrm{Fe}\mathrm{CN}_6\right)^{4-}$, $\left[\mathrm{Cu}\left(\mathrm{NH_3}\right)_4\right]^{2+}$ and $\left[\mathrm{PtCl_4}\right]^{2-}$. (The chemistry of complex compounds is dealt with in detail in Unit 9). The transition metals form a large number of complex compounds. This is due to the comparatively smaller sizes of the metal ions, their high ionic charges and the availability of d orbitals for bond formation.
8.3.12 Catalytic Properties
The transition metals and their compounds are known for their catalytic activity. This activity is ascribed to their ability to adopt multiple oxidation states and to form complexes. Vanadium(V) oxide (in Contact Process), finely divided iron (in Haber’s Process), and nickel (in Catalytic Hydrogenation) are some of the examples. Catalysts at a solid surface involve the formation of bonds between reactant molecules and atoms of the surface of the catalyst (first row transition metals utilise 3d and 4s electrons for bonding). This has the effect of increasing the concentration of the reactants at the catalyst surface and also weakening of the bonds in the reacting molecules (the activation energy is lowering). Also because the transition metal ions can change their oxidation states, they become more effective as catalysts. For example, iron(III) catalyses the reaction between iodide and persulphate ions.
$$ 2 \mathrm{I}^{-}+\mathrm{S_2} \mathrm{O_8}{ }^{2-} \rightarrow \mathrm{I_2}+2 \mathrm{SO_4}{ }^{2-} $$
An explanation of this catalytic action can be given as:
$$ \begin{aligned} & 2 \mathrm{Fe}^{3+}+2 \mathrm{I}^{-} \rightarrow 2 \mathrm{Fe}^{2+}+\mathrm{I_2} \\ & 2 \mathrm{Fe}^{2+}+\mathrm{S_2} \mathrm{O_8}{ }^{2-} \rightarrow 2 \mathrm{Fe}^{3+}+2 \mathrm{SO_4}{ }^{2-} \end{aligned} $$
8.3.13 Formation of Interstitial Compounds
Interstitial compounds are those which are formed when small atoms like $\mathrm{H}, \mathrm{C}$ or $\mathrm{N}$ are trapped inside the crystal lattices of metals. They are usually non stoichiometric and are neither typically ionic nor covalent, for example, TiC, $\mathrm{Mn_4} \mathrm{~N}, \mathrm{Fe_3} \mathrm{H}, \mathrm{VH_0.56}$ and $\mathrm{TiH_1.7}$, etc. The formulas quoted do not, of course, correspond to any normal oxidation state of the metal. Because of the nature of their composition, these compounds are referred to as interstitial compounds. The principal physical and chemical characteristics of these compounds are as follows:
(i) They have high melting points, higher than those of pure metals.
(ii) They are very hard, some borides approach diamond in hardness.
(iii) They retain metallic conductivity.
(iv) They are chemically inert.
8.3.14 Alloy Formation
An alloy is a blend of metals prepared by mixing the components. Alloys may be homogeneous solid solutions in which the atoms of one metal are distributed randomly among the atoms of the other. Such alloys are formed by atoms with metallic radii that are within about 15 percent of each other. Because of similar radii and other characteristics of transition metals, alloys are readily formed by these metals. The alloys so formed are hard and have often high melting points. The best known are ferrous alloys: chromium, vanadium, tungsten, molybdenum and manganese are used for the production of a variety of steels and stainless steel. Alloys of transition metals with non transition metals such as brass (copper-zinc) and bronze (copper-tin), are also of considerable industrial importance.
Example 8.9 What is meant by ‘disproportionation’ of an oxidation state? Give an example.
Solution When a particular oxidation state becomes less stable relative to other oxidation states, one lower, one higher, it is said to undergo disproportionation. For example, manganese (VI) becomes unstable relative to manganese(VII) and manganese (IV) in acidic solution.
$$ 3 \mathrm{Mn}^{\mathrm{VI}} \mathrm{O_4} ^{2-}+4 \mathrm{H}^{+} \rightarrow 2 \mathrm{Mn}^{\mathrm{VII}} \mathrm{O_4}^-+\mathrm{Mn}^{\mathrm{IV}} \mathrm{O_2}+2 \mathrm{H_2} \mathrm{O} $$
Intext Question
8.9 Explain why $\mathrm{Cu}^{+}$ ion is not stable in aqueous solutions?
Show Answer
Answer
In an aqueous medium, $\mathrm{Cu}^{2+}$ is more stable than $\mathrm{Cu}^{+}$. This is because although energy is required to remove one electron from $\mathrm{Cu}^{+}$to $\mathrm{Cu}^{2+}$, high hydration energy of $\mathrm{Cu2+}$ compensates for it. Therefore, $\mathrm{Cu}^{+}$ion in an aqueous solution is unstable. It disproportionates to give $\mathrm{Cu}^{2+}$ and $\mathrm{Cu}$.
$2 \mathrm{Cu _{(a q)}}^{+} \longrightarrow \mathrm{Cu}^{2+}{ _{(a q)}}+\mathrm{Cu _{(s)}}$
8.4 Some Important Compounds of Transition Elements
8.4.1 Oxides and Oxoanions of Metals
These oxides are generally formed by the reaction of metals with oxygen at high temperatures. All the metals except scandium form MO oxides which are ionic. The highest oxidation number in the oxides, coincides with the group number and is attained in $\mathrm{Sc_2} \mathrm{O_3}$ to $\mathrm{Mn_2} \mathrm{O_7}$. Beyond group 7, no higher oxides of iron above $\mathrm{Fe_2} \mathrm{O_3}$ are known. Besides the oxides, the oxocations stabilise $\mathrm{V}^{\mathrm{V}}$ as $\mathrm{VO_2}{ }^{+}, \mathrm{V}^{\mathrm{VV}}$ as $\mathrm{VO}^{2+}$ and $\mathrm{Ti}^{\mathrm{IV}}$ as $\mathrm{TiO}^{2+}$.
As the oxidation number of a metal increases, ionic character decreases. In the case of $\mathrm{Mn}, \mathrm{Mn_2} \mathrm{O_7}$ is a covalent green oil. Even $\mathrm{CrO_3}$ and $\mathrm{V_2} \mathrm{O_5}$ have low melting points. In these higher oxides, the acidic character is predominant.
Thus, $\mathrm{Mn_2} \mathrm{O_7}$ gives $\mathrm{HMnO_4}$ and $\mathrm{CrO_3}$ gives $\mathrm{H_2} \mathrm{CrO_4}$ and $\mathrm{H_2} \mathrm{Cr_2} \mathrm{O_7}$. $\mathrm{V_2} \mathrm{O_5}$ is, however, amphoteric though mainly acidic and it gives $\mathrm{VO_4}{ }^{3-}$ as well as $\mathrm{VO_2}{ }^{+}$ salts. In vanadium there is gradual change from the basic $\mathrm{V_2} \mathrm{O_3}$ to less basic $\mathrm{V_2} \mathrm{O_4}$ and to amphoteric $\mathrm{V_2} \mathrm{O_5}$. $\mathrm{V_2} \mathrm{O_4}$ dissolves in acids to give $\mathrm{VO}^{2+}$ salts. Similarly, $\mathrm{V_2} \mathrm{O_5}$ reacts with alkalies as well as acids to give $\mathrm{VO_4}^{3-}$ and $\mathrm{VO_4}^{+}$ respectively. The well characterised $\mathrm{CrO}$ is basic but $\mathrm{Cr_2} \mathrm{O_3}$ is amphoteric.
Potassium dichromate is a very important chemical used in leather industry and as an oxidant for preparation of many azo compounds. Dichromates are generally prepared from chromate, which in turn are obtained by the fusion of chromite ore $\left(\mathrm{FeCr_2} \mathrm{O_4}\right)$ with sodium or potassium carbonate in free access of air. The reaction with sodium carbonate occurs as follows:
$$ 4 \mathrm{FeCr_2} \mathrm{O_4}+8 \mathrm{Na_2} \mathrm{CO_3}+7 \mathrm{O_2} \rightarrow 8 \mathrm{Na_2} \mathrm{CrO_4}+2 \mathrm{Fe_2} \mathrm{O_3}+8 \mathrm{CO_2} $$
The yellow solution of sodium chromate is filtered and acidified with sulphuric acid to give a solution from which orange sodium dichromate, $\mathrm{Na_2} \mathrm{Cr_2} \mathrm{O_7} \cdot 2 \mathrm{H_2} \mathrm{O}$ can be crystallised.
$$ 2 \mathrm{Na_2} \mathrm{CrO_4}+2 \mathrm{H}^{+} \rightarrow \mathrm{Na_2} \mathrm{Cr_2} \mathrm{O_7}+2 \mathrm{Na}^{+}+\mathrm{H_2} \mathrm{O} $$
Sodium dichromate is more soluble than potassium dichromate. The latter is therefore, prepared by treating the solution of sodium dichromate with potassium chloride.
$$ \mathrm{Na_2} \mathrm{Cr_2} \mathrm{O_7}+2 \mathrm{KCl} \rightarrow \mathrm{K_2} \mathrm{Cr_2} \mathrm{O_7}+2 \mathrm{NaCl} $$
Orange crystals of potassium dichromate crystallise out. The chromates and dichromates are interconvertible in aqueous solution depending upon $\mathrm{pH}$ of the solution. The oxidation state of chromium in chromate and dichromate is the same.
$$ \begin{aligned} & 2 \mathrm{CrO_4}^{2-}+2 \mathrm{H}^{+} \rightarrow \mathrm{Cr_2} \mathrm{O_7}^{2-}+\mathrm{H_2} \mathrm{O} \\ & \mathrm{Cr_2} \mathrm{O_7}^{2-}+2 \mathrm{OH}^{-} \rightarrow 2 \mathrm{CrO_4}^{2-}+\mathrm{H_2} \mathrm{O} \end{aligned} $$
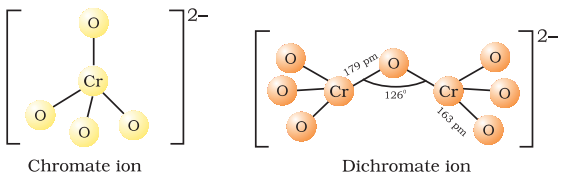
The structures of chromate ion, $\mathrm{CrO_4}{ }^{2-}$ and the dichromate ion, $\mathrm{Cr_2} \mathrm{O_7}{ }^{2-}$ are shown below. The chromate ion is tetrahedral whereas the dichromate ion consists of two tetrahedra sharing one corner with $\mathrm{Cr}-\mathrm{O}-\mathrm{Cr}$ bond angle of $126^{\circ}$.
Sodium and potassium dichromates are strong oxidising agents; the sodium salt has a greater solubility in water and is extensively used as an oxidising agent in organic chemistry. Potassium dichromate is used as a primary standard in volumetric analysis. In acidic solution, its oxidising action can be represented as follows:
$$ \mathrm{Cr_2} \mathrm{O_7}^{2-}+14 \mathrm{H}^{+}+6 \mathrm{e}^{-} \rightarrow 2 \mathrm{Cr}^{3+}+7 \mathrm{H_2} \mathrm{O}\left(E^{\ominus}=1.33 \mathrm{~V}\right) $$
Thus, acidified potassium dichromate will oxidise iodides to iodine, sulphides to sulphur, tin(II) to tin(IV) and iron(II) salts to iron(III). The half-reactions are noted below:
$$ \begin{aligned} & 6 \mathrm{I}^{-} \rightarrow 3 \mathrm{I} _{2}+6 \mathrm{e}^{-} \\ & 3 \mathrm{H} _{2} \mathrm{~S} _{2+} \rightarrow 6 \mathrm{H}^{+}+3 \mathrm{~S}+6 \mathrm{e}^{-} \\ & 3 \mathrm{Sn}^{-+} \rightarrow 3 \mathrm{Sn}^{4+}+6 \mathrm{e}^{-} \\ & 6 \mathrm{Fe}^{2+} \rightarrow 6 \mathrm{Fe}^{3+}+6 \mathrm{e}^{-} \end{aligned} $$
The full ionic equation may be obtained by adding the half-reaction for potassium dichromate to the half-reaction for the reducing agent, for e.g.,
$$ \mathrm{Cr_2} \mathrm{O_7}^{2-}+14 \mathrm{H}^{+}+6 \mathrm{Fe}^{2+} \rightarrow 2 \mathrm{Cr}^{3+}+6 \mathrm{Fe}^{3+}+7 \mathrm{H_2} \mathrm{O} $$
Potassium permanganate $\small{\mathbf{K M n O_4}}$
Potassium permanganate is prepared by fusion of $\mathrm{MnO_2}$ with an alkali metal hydroxide and an oxidising agent like $\mathrm{KNO_3}$. This produces the dark green $\mathrm{K_2} \mathrm{MnO_4}$ which disproportionates in a neutral or acidic solution to give permanganate.
$$ \begin{aligned} & 2 \mathrm{MnO_2}+4 \mathrm{KOH}+\mathrm{O_2} \rightarrow 2 \mathrm{~K_2} \mathrm{MnO_4}+2 \mathrm{H_2} \mathrm{O} \\ & 3 \mathrm{MnO_4}{ }^{2-}+4 \mathrm{H}^{+} \rightarrow 2 \mathrm{MnO_4}{ }^{-}+\mathrm{MnO_2}+2 \mathrm{H_2} \mathrm{O} \end{aligned} $$
Commercially it is prepared by the alkaline oxidative fusion of $\mathrm{MnO_2}$ followed by the electrolytic oxidation of manganate (Vl).
In the laboratory, a manganese (II) ion salt is oxidised by peroxodisulphate to permanganate.
$$ 2 \mathrm{Mn}^{2+}+5 \mathrm{~S_2} \mathrm{O_8}^{2-}+8 \mathrm{H_2} \mathrm{O} \rightarrow 2 \mathrm{MnO_4}^{-}+10 \mathrm{SO_4}{ }^{2-}+16 \mathrm{H}^{+} $$
Potassium permanganate forms dark purple (almost black) crystals which are isostructural with those of $\mathrm{KClO_4}$. The salt is not very soluble in water $(6.4 \mathrm{~g} / 100 \mathrm{~g}$ of water at $293 \mathrm{~K})$, but when heated it decomposes at $513 \mathrm{~K}$.
$$ 2 \mathrm{KMnO_4} \rightarrow \mathrm{K_2} \mathrm{MnO_4}+\mathrm{MnO_2}+\mathrm{O_2} $$
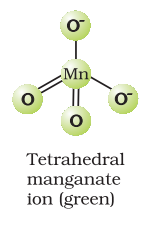
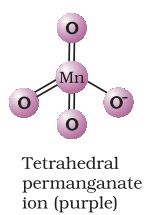
It has two physical properties of considerable interest: its intense colour and its diamagnetism along with temperature-dependent weak paramagnetism. These can be explained by the use of molecular orbital theory which is beyond the present scope.
The manganate and permanganate ions are tetrahedral; the $\pi$ bonding takes place by overlap of $p$ orbitals of oxygen with $d$ orbitals of manganese. The green manganate is paramagnetic because of one unpaired electron but the permanganate is diamagnetic due to the absence of unpaired electron.
Acidified permanganate solution oxidises oxalates to carbon dioxide, iron(II) to iron(III), nitrites to nitrates and iodides to free iodine. The half-reactions of reductants are:
$$ \begin{aligned} & 5 \underset{\mathrm{COO}^{-}}{\mathrm{COO}^{-}} \rightarrow 10 \mathrm{CO}_2+10 \mathrm{e} \\ & 5 \mathrm{Fe}^{2+} \rightarrow 5 \mathrm{Fe}^{3+}+5 \mathrm{e}^{-} \\ & 5 \mathrm{NO}_2{ }^{-}+5 \mathrm{H}_2 \mathrm{O} \rightarrow 5 \mathrm{NO}_3^{-}+10 \mathrm{H}^{+}+10 \mathrm{e}^{-} \\ & 10 \mathrm{I}^{-} \rightarrow 5 \mathrm{I}_2+10 \mathrm{e}^{-} \\ & \end{aligned} $$
The full reaction can be written by adding the half-reaction for $\mathrm{KMnO_4}$ to the half-reaction of the reducing agent, balancing wherever necessary.
If we represent the reduction of permanganate to manganate, manganese dioxide and manganese(II) salt by half-reactions,
$$ \begin{array}{ll} \mathrm{MnO_4}^{-}+\mathrm{e}^{-} \rightarrow \mathrm{MnO_4}{ }^{2-} & \left(E^{\ominus}=+0.56 \mathrm{~V}\right) \\ \mathrm{MnO_4}^{-}+4 \mathrm{H}^{+}+3 \mathrm{e}^{-} \rightarrow \mathrm{MnO_2}+2 \mathrm{H_2} \mathrm{O} & \left(E^{\ominus}=+1.69 \mathrm{~V}\right) \\ \mathrm{MnO_4}^{-}+8 \mathrm{H}^{+}+5 \mathrm{e}^{-} \rightarrow \mathrm{Mn}^{2+}+4 \mathrm{H_2} \mathrm{O} & \left(E^{\ominus}=+1.52 \mathrm{~V}\right) \end{array} $$
We can very well see that the hydrogen ion concentration of the solution plays an important part in influencing the reaction. Although many reactions can be understood by consideration of redox potential, kinetics of the reaction is also an important factor. Permanganate at $\left[\mathrm{H}^{+}\right]=1$ should oxidise water but in practice the reaction is extremely slow unless either manganese(11) ions are present or the temperature is raised.
A few important oxidising reactions of $\mathrm{KMnO_4}$ are given below:
1. In acid solutions:
(a) Iodine is liberated from potassium iodide :
$$ 10 \mathrm{I}^{-}+2 \mathrm{MnO_4}^{-}+16 \mathrm{H}^{+} \rightarrow 2 \mathrm{Mn}^{2+}+8 \mathrm{H_2} \mathrm{O}+5 \mathrm{I_2} $$
(b) $\mathrm{Fe}^{2+}$ ion (green) is converted to $\mathrm{Fe}^{3+}$ (yellow):
$$ 5 \mathrm{Fe}^{2+}+\mathrm{MnO_4}^{-}+8 \mathrm{H}^{+} \rightarrow \mathrm{Mn}^{2+}+4 \mathrm{H_2} \mathrm{O}+5 \mathrm{Fe}^{3+} $$
(c) Oxalate ion or oxalic acid is oxidised at $333 \mathrm{~K}$ :
$$ 5 \mathrm{C_2} \mathrm{O_4}{ }^{2-}+2 \mathrm{MnO_4}^{-}+16 \mathrm{H}^{+} \longrightarrow 2 \mathrm{Mn}^{2+}+8 \mathrm{H_2} \mathrm{O}+10 \mathrm{CO_2} $$
(d) Hydrogen sulphide is oxidised, sulphur being precipitated:
$$ \begin{aligned} & \mathrm{H_2} \mathrm{~S} \longrightarrow 2 \mathrm{H}^{+}+\mathrm{S}^{2-} \\ & 5 \mathrm{~S}^{2-}+2 \mathrm{MnO_4}^{-}+16 \mathrm{H}^{+} \longrightarrow 2 \mathrm{Mn}^{2+}+8 \mathrm{H_2} \mathrm{O}+5 \mathrm{~S} \end{aligned} $$
(e) Sulphurous acid or sulphite is oxidised to a sulphate or sulphuric acid:
$$ 5 \mathrm{SO_3}{ }^{2-}+2 \mathrm{MnO_4}{ }^{-}+6 \mathrm{H}^{+} \longrightarrow 2 \mathrm{Mn}^{2+}+3 \mathrm{H_2} \mathrm{O}+5 \mathrm{SO_4}{ }^{2-} $$
(f) Nitrite is oxidised to nitrate:
$$ 5 \mathrm{NO_2}^{-}+2 \mathrm{MnO_4}^{-}+6 \mathrm{H}^{+} \longrightarrow 2 \mathrm{Mn}^{2+}+5 \mathrm{NO_3}^{-}+3 \mathrm{H_2} \mathrm{O} $$
2. In neutral or faintly alkaline solutions:
(a) A notable reaction is the oxidation of iodide to iodate:
$$ 2 \mathrm{MnO_4}^{-}+\mathrm{H_2} \mathrm{O}+\mathrm{I}^{-} \longrightarrow 2 \mathrm{MnO_2}+2 \mathrm{OH}^{-}+\mathrm{IO_3}^{-} $$
(b) Thiosulphate is oxidised almost quantitatively to sulphate:
$$ 8 \mathrm{MnO_4}{ }^{-}+3 \mathrm{~S_2} \mathrm{O_3}{ }^{2-}+\mathrm{H_2} \mathrm{O} \longrightarrow 8 \mathrm{MnO_2}+6 \mathrm{SO_4}{ }^{2-}+2 \mathrm{OH} $$
(c) Manganous salt is oxidised to $\mathrm{MnO_2}$; the presence of zinc sulphate or zinc oxide catalyses the oxidation:
$$ 2 \mathrm{MnO_4}^{-}+3 \mathrm{Mn}^{2+}+2 \mathrm{H_2} \mathrm{O} \longrightarrow 5 \mathrm{MnO_2}+4 \mathrm{H}^{+} $$
Note: Permanganate titrations in presence of hydrochloric acid are unsatisfactory since hydrochloric acid is oxidised to chlorine.
Uses: Besides its use in analytical chemistry, potassium permanganate is used as a favourite oxidant in preparative organic chemistry. Its uses for the bleaching of wool, cotton, silk and other textile fibres and for the decolourisation of oils are also dependent on its strong oxidising power.
THE INNER TRANSITION ELEMENTS ( $f$-BLOCK)
The f-block consists of the two series, lanthanoids (the fourteen elements following lanthanum) and actinoids (the fourteen elements following actinium). Because lanthanum closely resembles the lanthanoids, it is usually included in any discussion of the lanthanoids for which the general symbol Ln is often used. Similarly, a discussion of the actinoids includes actinium besides the fourteen elements constituting the series. The lanthanoids resemble one another more closely than do the members of ordinary transition elements in any series. They have only one stable oxidation state and their chemistry provides an excellent opportunity to examine the effect of small changes in size and nuclear charge along a series of otherwise similar elements. The chemistry of the actinoids is, on the other hand, much more complicated. The complication arises partly owing to the occurrence of a wide range of oxidation states in these elements and partly because their radioactivity creates special problems in their study; the two series will be considered separately here.
8.5 The Lanthanoids
The names, symbols, electronic configurations of atomic and some ionic states and atomic and ionic radii of lanthanum and lanthanoids (for which the general symbol Ln is used) are given in Table 8.9.
8.5.1 Electronic Configurations
It may be noted that atoms of these elements have electronic configuration with $6 s^{2}$ common but with variable occupancy of $4 f$ level (Table 8.9). However, the electronic configurations of all the tripositive ions (the most stable oxidation state of all the lanthanoids) are of the form $4 f^{\mathrm{n}}$ ( $\mathrm{n}=1$ to 14 with increasing atomic number).
8.5.2 Atomic and Ionic Sizes
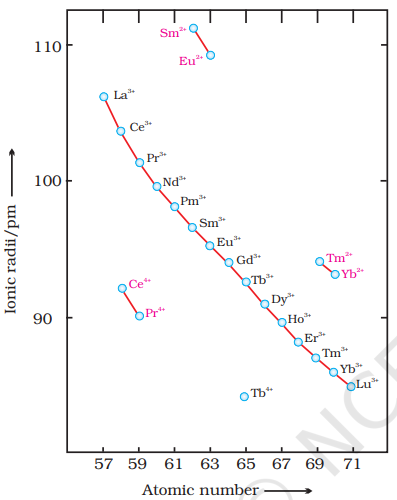
Fig. 8.6: Trends in ionic radii of lanthanoids
The overall decrease in atomic and ionic radii from lanthanum to lutetium (the lanthanoid contraction) is a unique feature in the chemistry of the lanthanoids. It has far reaching consequences in the chemistry of the third transition series of the elements. The decrease in atomic radii (derived from the structures of metals) is not quite regular as it is regular in $\mathrm{M}^{3+}$ ions (Fig. 8.6). This contraction is, of course, similar to that observed in an ordinary transition series and is attributed to the same cause, the imperfect shielding of one electron by another in the same sub-shell. However, the shielding of one $4 f$ electron by another is less than one $d$ electron by another with the increase in nuclear charge along the series. There is fairly regular decrease in the sizes with increasing atomic number.
The cumulative effect of the contraction of the lanthanoid series, known as lanthanoid contraction, causes the radii of the members of the third transition series to be very similar to those of the corresponding members of the second series. The almost identical radii of $\mathrm{Zr}$ $(160 \mathrm{pm})$ and $\mathrm{Hf}(159 \mathrm{pm})$, a consequence of the lanthanoid contraction, account for their occurrence together in nature and for the difficulty faced in their separation.
8.5.3 Oxidation States
In the lanthanoids, $\mathrm{La}(\mathrm{II})$ and $\mathrm{Ln}$ (III) compounds are predominant species. However, occasionally +2 and +4 ions in solution or in solid compounds are also obtained. This irregularity (as in ionisation enthalpies) arises mainly from the extra stability of empty, half-filled or filled $f$ subshell. Thus, the formation of $\mathrm{Ce}^{\mathrm{IV}}$ is favoured by its noble gas configuration, but it is a strong oxidant reverting to the common +3 state. The $E^{\circ}$ value for $\mathrm{Ce}^{4+} / \mathrm{Ce}^{3+}$ is $+1.74 \mathrm{~V}$ which suggests that it can oxidise water. However, the reaction rate is very slow and hence Ce(IV) is a good analytical reagent. Pr, Nd, Tb and Dy also exhibit +4 state but only in oxides, $\mathrm{MO_2} . \mathrm{Eu}^{2+}$ is formed by losing the two $s$ electrons and its $f^{7}$ configuration accounts for the formation of this ion. However, $\mathrm{Eu}^{2+}$ is a strong reducing agent changing to the common +3 state. Similarly $\mathrm{Yb}^{2+}$ which has $f^{14}$ configuration is a reductant. $\mathrm{Tb}^{\mathrm{IV}}$ has half-filled $f$-orbitals and is an oxidant. The behaviour of samarium is very much like europium, exhibiting both +2 and +3 oxidation states.
Table 8.9: Electronic Configurations and Radii of Lanthanum and Lanthanoids
| Atomic Number |
Name | Symbol | Electronic configurations* | Radii/pm | ||||
|---|---|---|---|---|---|---|---|---|
| $\mathbf{Ln}$ | $\mathbf{L n}^{2+}$ | $\mathbf{L n}^{3+}$ | $\mathbf{L n}^{4+}$ | Ln | $\mathbf{L n}^{3+}$ | |||
| 57 | Lanthanum | $\mathrm{La}$ | $5 d^1 6 s^2$ | $5 d^1$ | $4 f^{\circ}$ | 187 | 106 | |
| 58 | Cerium | $\mathrm{Ce}$ | $4 f^2 5 d^1 6 \mathrm{~s}^2$ | $4 f^2$ | $4 f^1$ | $4 f^{\circ}$ | 183 | 103 |
| 59 | Praseodymium | $\operatorname{Pr}$ | $4 f^3 6 \mathrm{~s}^2$ | $4 f^3$ | $4 f^2$ | $4 f^1$ | 182 | 101 |
| 60 | Neodymium | $\mathrm{Nd}$ | $4 f^4 6 \mathrm{~s}^2$ | $4 f^4$ | $4 f^3$ | $4 f^2$ | 181 | 99 |
| 61 | Promethium | $\operatorname{Pm}$ | $4 f^5 6 \mathrm{~s}^2$ | $4 f^5$ | $4 f^4$ | 181 | 98 | |
| 62 | Samarium | Sm | $4 f^6 6 \mathrm{~s}^2$ | $4 f^6$ | $4 f^5$ | 180 | 96 | |
| 63 | Europium | $\mathrm{Eu}$ | $4 f^7 6 \mathrm{~s}^2$ | $4 f^7$ | $4 f^6$ | 199 | 95 | |
| 64 | Gadolinium | $\mathrm{Gd}$ | $4 f^7 5 d^1 6 s^2$ | $4 f^7 5 d^1$ | $4 f^7$ | 180 | 94 | |
| 65 | Terbium | $\mathrm{Tb}$ | $4 f^9 6 \mathrm{~s}^2$ | $4 f^9$ | $4 f^8$ | $4 f^7$ | 178 | 92 |
| 66 | Dysprosium | Dy | $4 f^{10} 6 \mathrm{~s}^2$ | $4 f^{10}$ | $4 f^9$ | $4 f^8$ | 177 | 91 |
| 67 | Holmium | Ho | $4 f^{11} 6 \mathrm{~s}^2$ | $4 f^{11}$ | $4 f^{10}$ | 176 | 89 | |
| 68 | Erbium | $\mathrm{Er}$ | $4 f^{12} 6 \mathrm{~s}^2$ | $4 f^{12}$ | $4 f^{11}$ | 175 | 88 | |
| 69 | Thulium | $\mathrm{Tm}$ | $4 f^{13} 6 \mathrm{~s}^2$ | $4 f^{13}$ | $4 f^{12}$ | 174 | 87 | |
| 70 | Ytterbium | $\mathrm{Yb}$ | $4 f^{14} 6 \mathrm{~s}^2$ | $4 f^{14}$ | $4 f^{13}$ | 173 | 86 | |
| 71 | Lutetium | Lu | $4 f^{14} 5 d^1 6 s^2$ | $4 f^{14} 5 d^1$ | $4 f^{14}$ | - | - |
- Only electrons outside $[\mathrm{Xe}]$ core are indicated
8.5.4 General Characteristics
All the lanthanoids are silvery white soft metals and tarnish rapidly in air. The hardness increases with increasing atomic number, samarium being steel hard. Their melting points range between 1000 to $1200 \mathrm{~K}$ but samarium melts at $1623 \mathrm{~K}$. They have typical metallic structure and are good conductors of heat and electricity. Density and other properties change smoothly except for $\mathrm{Eu}$ and $\mathrm{Yb}$ and occasionally for $\mathrm{Sm}$ and $\mathrm{Tm}$.
Many trivalent lanthanoid ions are coloured both in the solid state and in aqueous solutions. Colour of these ions may be attributed to the presence of $f$ electrons. Neither $\mathrm{La}^{3+}$ nor $\mathrm{Lu}^{3+}$ ion shows any colour but the rest do so. However, absorption bands are narrow, probably because of the excitation within $f$ level. The lanthanoid ions other than the $f^{0}$ type $\left(\mathrm{La}^{3+}\right.$ and $\left.\mathrm{Ce}^{4+}\right)$ and the $f^{14}$ type $\left(\mathrm{Yb}^{2+}\right.$ and $\left.\mathrm{Lu}^{3+}\right)$ are all paramagnetic.
The first ionisation enthalpies of the lanthanoids are around $600 \mathrm{~kJ} \mathrm{~mol}^{-1}$, the second about $1200 \mathrm{~kJ} \mathrm{~mol}^{-1}$ comparable with those of calcium. A detailed discussion of the variation of the third ionisation enthalpies indicates that the exchange enthalpy considerations (as in $3 d$ orbitals of the first transition series), appear to impart a certain degree of stability to empty, half-filled and completely filled orbitals $f$ level. This is indicated from the abnormally low value of the third ionisation enthalpy of lanthanum, gadolinium and lutetium.
In their chemical behaviour, in general, the earlier members of the series are quite reactive similar to calcium but, with increasing atomic number, they behave more like aluminium. Values for $E^{\ominus}$ for the half-reaction:
$ \mathrm{Ln}^{3+}(\mathrm{aq})+3 \mathrm{e}^{-} \rightarrow \operatorname{Ln}(\mathrm{s}) $ are in the range of –2.2 to –2.4 V except for Eu for which the value is - 2.0 V. This is, of course, a small variation. The metals combine with hydrogen when gently heated in the gas. The carbides, Ln3C, Ln2C3 and LnC2 are formed when the metals are heated with carbon. They liberate hydrogen from dilute acids and burn in halogens to form halides. They form oxides M2O3 and hydroxides M(OH)3. The hydroxides are definite compounds, not just hydrated oxides. They are basic like alkaline earth metal oxides and hydroxides. Their general reactions are depicted in Fig. 8.7.
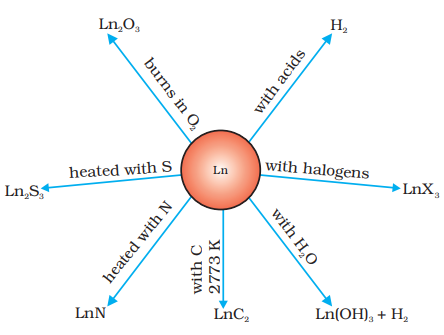
Fig. 8.7: Chemical reactions of the lanthanoids.
The best single use of the lanthanoids is for the production of alloy steels for plates and pipes. A well known alloy is mischmetall which consists of a lanthanoid metal (~ 95%) and iron (~ 5%) and traces of S, C, Ca and Al. A good deal of mischmetall is used in Mg-based alloy to produce bullets, shell and lighter flint. Mixed oxides of lanthanoids are employed as catalysts in petroleum cracking. Some individual Ln oxides are used as phosphors in television screens and similar fluorescing surfaces.
8.6 The Actinoids
Table 8.10: Some Properties of Actinium and Actinoids
| Atomic Number |
Name | Symbol | Electronic conifigurations* | Radii/pm | |||
|---|---|---|---|---|---|---|---|
| ${\mathbf{M}}$ | $\mathbf{M}^{3+}$ | ${\mathbf{M}^{3+}}$ | ${\mathbf{M}^{3+}}$ | ${\mathbf{M}^{4+}}$ | |||
| 89 | Actinium | $\mathrm{Ac}$ | $6 d^1 7 s^2$ | $5 f^{\circ}$ | 111 | ||
| 90 | Thorium | Th | $6 d^2 7 s^2$ | $5 f^1$ | $5 f^{\circ}$ | 99 | |
| 91 | Protactinium | $\mathrm{Pa}$ | $5 f^2 6 d^1 7 s^2$ | $5 f^2$ | $5 f^1$ | 96 | |
| 92 | Uranium | $\mathrm{U}$ | $5 f^3 6 d^1 7 s^2$ | $5 f^3$ | $5 f^2$ | 103 | 93 |
| 93 | Neptunium | $\mathrm{Np}$ | $5 f^4 6 d^1 7 s^2$ | $5 f^4$ | $5 f^3$ | 101 | 92 |
| 94 | Plutonium | $\mathrm{Pu}$ | $5 f^6 7 s^2$ | $5 f^5$ | $5 f^4$ | 100 | 90 |
| 95 | Americium | Am | $5 f^7 7 s^2$ | $5 f^6$ | $5 f^5$ | 99 | 89 |
| 96 | Curium | $\mathrm{Cm}$ | $5 f^7 6 d^1 7 s^2$ | $5 f^7$ | $5 f^6$ | 99 | 88 |
| 97 | Berkelium | $\mathrm{Bk}$ | $5 f^9 7 s^2$ | $5 f^8$ | $5 f^7$ | 98 | 87 |
| 98 | Californium | Cf | $5 f^{10} 7 s^2$ | $5 f^9$ | $5 f^8$ | 98 | 86 |
| 99 | Einstenium | Es | $5 f^{11} 7 \mathrm{~s}^2$ | $5 f^{10}$ | $5 f^9$ | - | - |
| 100 | Fermium | $\mathrm{Fm}$ | $5 f^{12} 7 s^2$ | $5 f^{11}$ | $5 f^{10}$ | - | - |
| 101 | Mendelevium | Md | $5 f^{13} 7 s^2$ | $5 f^{12}$ | $5 f^{11}$ | - | - |
| 102 | Nobelium | No | $5 f^{14} 7 s^2$ | $5 f^{13}$ | $5 f^{12}$ | - | - |
| 103 | Lawrencium | $\mathrm{Lr}$ | $5 f^{14} 6 d^1 7 s^2$ | $5 f^{14}$ | $5 f^{13}$ | - | - |
The actinoids are radioactive elements and the earlier members have relatively long half-lives, the latter ones have half-life values ranging from a day to 3 minutes for lawrencium $(Z=103)$. The latter members could be prepared only in nanogram quantities. These facts render their study more difficult.
8.6.1 Electronic Configurations
All the actinoids are believed to have the electronic configuration of $7 \mathrm{~s}^{2}$ and variable occupancy of the $5 \mathrm{f}$ and $6 \mathrm{~d}$ subshells. The fourteen electrons are formally added to $5 f$, though not in thorium $(Z=90)$ but from $\mathrm{Pa}$ onwards the $5 f$ orbitals are complete at element 103. The irregularities in the electronic configurations of the actinoids, like those in the lanthanoids are related to the stabilities of the $f^{0}, f^{7}$ and $f^{14}$ occupancies of the $5 \mathrm{f}$ orbitals. Thus, the configurations of $\mathrm{Am}$ and $\mathrm{Cm}$ are $[\mathrm{Rn}] 5 f^{7} 7 s^{2}$ and $[\mathrm{Rn}] 5 f^{7} 6 d^{1} 7 s^{2}$. Although the $5 f$ orbitals resemble the $4 f$ orbitals in their angular part of the wave-function, they are not as buried as $4 f$ orbitals and hence $5 f$ electrons can participate in bonding to a far greater extent.
8.6.2 Ionic Sizes
The general trend in lanthanoids is observable in the actinoids as well. There is a gradual decrease in the size of atoms or $\mathrm{M}^{3+}$ ions across the series. This may be referred to as the actinoid contraction (like lanthanoid contraction). The contraction is, however, greater from element to element in this series resulting from poor shielding by $5 f$ electrons.
8.6.3 Oxidation States
There is a greater range of oxidation states, which is in part attributed to the fact that the $5 f, 6 d$ and $7 \mathrm{~s}$ levels are of comparable energies. The known oxidation states of actinoids are listed in Table 8.11.
The actinoids show in general +3 oxidation state. The elements, in the first half of the series frequently exhibit higher oxidation states. For example, the maximum oxidation state increases from +4 in $\mathrm{Th}$ to $+5,+6$ and +7 respectively in $\mathrm{Pa}, \mathrm{U}$ and $\mathrm{Np}$ but decreases in succeeding elements (Table 8.11). The actinoids resemble the lanthanoids in having more compounds in +3 state than in the +4 state. However, +3 and +4 ions tend to hydrolyse. Because the distribution of oxidation states among the actinoids is so uneven and so different for the former and later elements, it is unsatisfactory to review their chemistry in terms of oxidation states.
Table 8.11: Oxidation States of Actinium and Actinoids
| Ac | Th | Pa | U | Np | Pu | Am | Cm | Bk | Cf | Ds | Fm | Md | No | Lr | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | ||
| 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | ||||||||
| 5 | 5 | 5 | 5 | 5 | |||||||||||
| 6 | 6 | 6 | 6 | ||||||||||||
| 7 | 7 | ||||||||||||||
| 7 |
8.6.4 General Characteristics and Comparison with Lanthanoids
The actinoid metals are all silvery in appearance but display a variety of structures. The structural variability is obtained due to irregularities in metallic radii which are far greater than in lanthanoids.
The actinoids are highly reactive metals, especially when finely divided. The action of boiling water on them, for example, gives a mixture of oxide and hydride and combination with most non metals takes place at moderate temperatures. Hydrochloric acid attacks all metals but most are slightly affected by nitric acid owing to the formation of protective oxide layers; alkalies have no action.
The magnetic properties of the actinoids are more complex than those of the lanthanoids. Although the variation in the magnetic susceptibility of the actinoids with the number of unpaired 5 f electrons is roughly parallel to the corresponding results for the lanthanoids, the latter have higher values.
It is evident from the behaviour of the actinoids that the ionisation enthalpies of the early actinoids, though not accurately known, but are lower than for the early lanthanoids. This is quite reasonable since it is to be expected that when 5f orbitals are beginning to be occupied, they will penetrate less into the inner core of electrons. The 5f electrons, will therefore, be more effectively shielded from the nuclear charge than the 4f electrons of the corresponding lanthanoids. Because the outer electrons are less firmly held, they are available for bonding in the actinoids.
A comparison of the actinoids with the lanthanoids, with respect to different characteristics as discussed above, reveals that behaviour similar to that of the lanthanoids is not evident until the second half of the actinoid series. However, even the early actinoids resemble the lanthanoids in showing close similarities with each other and in gradual variation in properties which do not entail change in oxidation state. The lanthanoid and actinoid contractions, have extended effects on the sizes, and therefore, the properties of the elements succeeding them in their respective periods. The lanthanoid contraction is more important because the chemistry of elements succeeding the actinoids are much less known at the present time.
Intext Question
8.9 Explain why $\mathrm{Cu}^{+}$ ion is not stable in aqueous solutions?
Show Answer
Answer
In an aqueous medium, $\mathrm{Cu}^{2+}$ is more stable than $\mathrm{Cu}^{+}$. This is because although energy is required to remove one electron from $\mathrm{Cu}^{+}$to $\mathrm{Cu}^{2+}$, high hydration energy of $\mathrm{Cu2+}$ compensates for it. Therefore, $\mathrm{Cu}^{+}$ion in an aqueous solution is unstable. It disproportionates to give $\mathrm{Cu}^{2+}$ and $\mathrm{Cu}$.
$2 \mathrm{Cu _{(a q)}}^{+} \longrightarrow \mathrm{Cu}^{2+}{ _{(a q)}}+\mathrm{Cu _{(s)}}$
8.7 Some Applications of d- and f-Block Elements
Iron and steels are the most important construction materials. Their production is based on the reduction of iron oxides, the removal of impurities and the addition of carbon and alloying metals such as $\mathrm{Cr}, \mathrm{Mn}$ and Ni. Some compounds are manufactured for special purposes such as TiO for the pigment industry and $\mathrm{MnO_2}$ for use in dry battery cells. The battery industry also requires $\mathrm{Zn}$ and $\mathrm{Ni} / \mathrm{Cd}$. The elements of Group 11 are still worthy of being called the coinage metals, although $\mathrm{Ag}$ and $\mathrm{Au}$ are restricted to collection items and the contemporary UK ‘copper’ coins are copper-coated steel. The ‘silver’ UK coins are a Cu/Ni alloy. Many of the metals and/or their compounds are essential catalysts in the chemical industry. $\mathrm{V_2} \mathrm{O_5}$ catalyses the oxidation of $\mathrm{SO_2}$ in the manufacture of sulphuric acid. $\mathrm{TiCl_4}$ with $\mathrm{Al}\left(\mathrm{CH_3}\right)_{3}$ forms the basis of the Ziegler catalysts used to manufacture polyethylene (polythene). Iron catalysts are used in the Haber process for the production of ammonia from $\mathrm{N_2} / \mathrm{H_2}$ mixtures. Nickel catalysts enable the hydrogenation of fats to proceed. In the Wacker process the oxidation of ethyne to ethanal is catalysed by $\mathrm{PdCl_2}$. Nickel complexes are useful in the polymerisation of alkynes and other organic compounds such as benzene. The photographic industry relies on the special light-sensitive properties of $\mathrm{AgBr}$.
Summary
The $d$-block consisting of Groups 3-12 occupies the large middle section of the periodic table. In these elements the inner $d$ orbitals are progressively filled. The $f$-block is placed outside at the bottom of the periodic table and in the elements of this block, $4 f$ and $5 f$ orbitals are progressively filled.
Corresponding to the filling of $3 d, 4 d$ and $5 d$ orbitals, three series of transition elements are well recognised. All the transition elements exhibit typical metallic properties such as -high tensile strength, ductility, malleability, thermal and electrical conductivity and metallic character. Their melting and boiling points are high which are attributed to the involvement of $(n-1) d$ electrons resulting into strong interatomic bonding. In many of these properties, the maxima occur at about the middle of each series which indicates that one unpaired electron per $d$ orbital is particularly a favourable configuration for strong interatomic interaction.
Successive ionisation enthalpies do not increase as steeply as in the main group elements with increasing atomic number. Hence, the loss of variable number of electrons from $(n-1) d$ orbitals is not energetically unfavourable. The involvement of $(\boldsymbol{n}-\mathbf{1}) d$ electrons in the behaviour of transition elements impart certain distinct characteristics to these elements. Thus, in addition to variable oxidation states, they exhibit paramagnetic behaviour, catalytic properties and tendency for the formation of coloured ions, interstitial compounds and complexes.
The transition elements vary widely in their chemical behaviour. Many of them are sufficiently electropositive to dissolve in mineral acids, although a few are ’noble’. Of the first series, with the exception of copper, all the metals are relatively reactive.
The transition metals react with a number of non-metals like oxygen, nitrogen, sulphur and halogens to form binary compounds. The first series transition metal oxides are generally formed from the reaction of metals with oxygen at high temperatures. These oxides dissolve in acids and bases to form oxometallic salts. Potassium dichromate and potassium permanganate are common examples. Potassium dichromate is prepared from the chromite ore by fusion with alkali in presence of air and acidifying the extract. Pyrolusite ore $\left(\mathrm{MnO_2}\right)$ is used for the preparation of potassium permanganate. Both the dichromate and the permanganate ions are strong oxidising agents.
The two series of inner transition elements, lanthanoids and actinoids constitute the $\boldsymbol{f}$-block of the periodic table. With the successive filling of the inner orbitals, $4 f$, there is a gradual decrease in the atomic and ionic sizes of these metals along the series (lanthanoid contraction). This has far reaching consequences in the chemistry of the elements succeeding them. Lanthanum and all the lanthanoids are rather soft white metals. They react easily with water to give solutions giving +3 ions. The principal oxidation state is +3 , although +4 and +2 oxidation states are also exhibited by some occasionally. The chemistry of the actinoids is more complex in view of their ability to exist in different oxidation staexercites. Furthermore, many of the actinoid elements are radioactive which make the study of these elements rather difficult.
There are many useful applications of the $d$ - and $f$-block elements and their compounds, notable among them being in varieties of steels, catalysts, complexes, organic syntheses, etc.
Exercises
8.1 Write down the electronic configuration of:
(i) $\mathrm{Cr}^{3+}+$
(ii) $\mathrm{Pm}^{3+}$
(iii) $\mathrm{Cu}^{+}$
(iv) $\mathrm{Ce}^{4+}$
(v) $\mathrm{Co}^{2}+$
(vi) $\mathrm{Lu}^{2+}$
(vii) $\mathrm{Mn}^{2+}$
(viii) $\mathrm{Th}^{4+}$
Show Answer
Answer
(i) $\mathrm{Cr}^{3+}: 1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{3}$
Or, $[\mathrm{Ar}]^{18} 3 d^{3}$
(ii) $\mathrm{Pm}^{3+}: 1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10} 4 s^{2} 4 p^{6} 4 d^{10} 5 s^{2} 5 p^{6} 4 f^{4}$
Or, $[\mathrm{Xe}]^{54} 3 d^{3}$
(iii) $\mathrm{Cu}^{+}: 1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10}$
Or, $[\operatorname{Ar}]^{18} 3 d^{10}$
(iv) $\mathrm{Ce}^{4+}: 1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10} 4 s^{2} 4 p^{6} 4 d^{10} 5 s^{2} 5 p^{6}$
Or, $[\mathrm{Xe}]^{54}$
(v) $\mathrm{Co}^{2+}: 1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{7}$
Or, $[\mathrm{Ar}]^{18} 3 d^{7}$
(vi) $\mathrm{Lu}^{2+}: 1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10} 4 s^{2} 4 p^{6} 4 d^{10} 5 s^{2} 5 p^{6} 4 f^{14} 5 d^{1}$
Or, $[X e]^{54} 2 f^{14} 3 d^{3}$
(vii) $\mathrm{Mn}^{2+}: 1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{5}$
8.2 Why are $\mathrm{Mn}^{2+}$ compounds more stable than $\mathrm{Fe}^{2+}$ towards oxidation to their +3 state?
Show Answer
Answer
Electronic configuration of $\mathrm{Mn}^{2+}$ is $[\mathrm{Ar}]^{18} 3 d^{5}$.
Electronic configuration of $\mathrm{Fe}^{2+}$ is $[\mathrm{Ar}]^{18} 3 d^{6}$.
It is known that half-filled and fully-filled orbitals are more stable. Therefore, $\mathrm{Mn}$ in (+2) state has a stabled ${ }^{5}$ configuration. This is the reason $\mathrm{Mn}^{2+}$ shows resistance to oxidation to $\mathrm{Mn}^{3+}$. Also, $\mathrm{Fe}^{2+}$ has $3 d^{6}$ configuration and by losing one electron, its configuration changes to a more stable $3 d^{5}$ configuration. Therefore, $\mathrm{Fe}^{2+}$ easily gets oxidized to $\mathrm{Fe}^{+3}$ oxidation state.
8.3 Explain briefly how +2 state becomes more and more stable in the first half of the first row transition elements with increasing atomic number?
Show Answer
Answer
Element (+2 state) $ _{21} \mathrm{Sc}^{2+} , _{22} \mathrm{Ti}^{2+} , _{23} \mathrm{~V}^{2+} , _{24} \mathrm{Cr}^{2+} , _{25} \mathrm{Mn}^{2+}$
Electronic configuration $3 d^1 3 d^2 3 d^3 3 d^4 3 d^5$
In all the elements listed, the removal of two $4 \mathrm{~s}$ electrons (in $\mathrm{Cr}^{2+}$ i.e., from $4 \mathrm{~s}$ and $1 e^{-}$from $3 d$ ), the $3 d$-orbitals get gradually occupied. Since, the number of empty d-orbitals decreases or the number of unpaired electrons in 3d-orbitals increases with increase in atomic number of cations, so the stability of the cations $\left(\mathrm{M}^{2+}\right)$ increases from $\mathrm{Sc}^{2+}$ to $\mathrm{Mn}^{2+}$
8.4 To what extent do the electronic configurations decide the stability of oxidation states in the first series of the transition elements? Illustrate your answer with examples.
Show Answer
Answer
The elements in the first-half of the transition series exhibit many oxidation states with Mn exhibiting maximum number of oxidation states ( +2 to +7 ). The stability of +2 oxidation state increases with the increase in atomic number. This happens as more electrons are getting filled in the $d$-orbital. However, $\mathrm{Sc}$ does not show +2 oxidation state. Its electronic configuration is $4 s^{2} 3 d^{1}$. It loses all the three electrons to form $\mathrm{Sc}^{3+} .+3$ oxidation state of $\mathrm{Sc}$ is very stable as by losing all three electrons, it attains stable noble gas configuration, $[\mathrm{Ar}]$. $\mathrm{Ti}(+4)$ and $\mathrm{V}(+5)$ are very stable for the same reason. For Mn, +2 oxidation state is very stable as after losing two electrons, its $d$-orbital is exactly halffilled, $[\mathrm{Ar}] 3 d^{5}$.
8.5 What may be the stable oxidation state of the transition element with the following $d$ electron configurations in the ground state of their atoms : $3 d^{3}$, $3 d^{5}, 3 d^{3}$ and $3 d^{4} ?$
Show Answer
Answer
| Electronic configuration in ground state | Stable oxidation states | |
|---|---|---|
| (i) | $3 d^{3}$ (Vanadium) | $+2,+3,+4$ and +5 |
| (ii) | $3 d^{5}$ (Chromium) | $+3,+4,+6$ |
| (iii) | $3 d^{5}$ (Manganese) | $+2,+4,+6,+7$ |
| (iv) | $3 d^{8}$ (Cobalt) | $+2,+3$ |
| (v) | $3 d^{4}$ | There is no $3d^{4}$ configuration in ground state. |
8.6 Name the oxometal anions of the first series of the transition metals in which the metal exhibits the oxidation state equal to its group number.
Show Answer
Answer
$\mathrm{MnO}_4^{-}: \mathrm{Mn}$ has +7 oxidation number and group number is 7 .
$\mathrm{CrO}_4^{2-}: \mathrm{Cr}$ has +6 oxidation state and group number is 6 .
$\mathrm{VO}_3^{-}: \mathrm{V}$ has +5 oxidation state and the group number is 5 .
8.7 What is lanthanoid contraction? What are the consequences of lanthanoid contraction?
Show Answer
Answer
As we move along the lanthanoid series, the atomic number increases gradually by one. This means that the number of electrons and protons present in an atom also increases by one. As electrons are being added to the same shell, the effective nuclear charge increases. This happens because the increase in nuclear attraction due to the addition of proton is more pronounced than the increase in the interelectronic repulsions due to the addition of electron. Also, with the increase in atomic number, the number of electrons in the 4 forbital also increases. The 4 felectrons have poor shielding effect. Therefore, the effective nuclear charge experienced by the outer electrons increases. Consequently, the attraction of the nucleus for the outermost electrons increases. This results in a steady decrease in the size of lanthanoids with the increase in the atomic number. This is termed as lanthanoid contraction.
Consequences of lanthanoid contraction
(i) There is similarity in the properties of second and third transition series.
ii. Separation of lanthanoids is possible due to lanthanide contraction.
(iii) It is due to lanthanide contraction that there is variation in the basic strength of lanthanide hydroxides. (Basic strength decreases from $\mathrm{La}\mathrm{(OH) _3}$ to $\mathrm{Lu}(\mathrm{OH}) _{3}$.)
8.8 What are the characteristics of the transition elements and why are they called transition elements? Which of the $d$-block elements may not be regarded as the transition elements?
Show Answer
Answer
Transition elements are those elements in which the atoms or ions (in stable oxidation state) contain partially filled $d$ orbital. These elements lie in the $d$-block and show a transition of properties between $s$-block and $p$-block. Therefore, these are called transition elements.
Elements such as $\mathrm{Zn}, \mathrm{Cd}$, and $\mathrm{Hg}$ cannot be classified as transition elements because these have completely filled $d$ subshell.
8.9 In what way is the electronic configuration of the transition elements different from that of the non-transition elements?
Show Answer
Answer
Transition metals have a partially filled $d$-orbital. Therefore, the electronic configuration of transition elements is ( $n$ 1) $d^{1-10} \mathrm{~ns}^{0.2}$.
The non-transition elements either do not have a $d$-orbital or have a fully filled $d$-orbital. Therefore, the electronic configuration of non-transition elements is $n s^{1-2}$ or $n s^{2} n p^{1-6}$.
8.10 What are the different oxidation states exhibited by the lanthanoids?
Show Answer
Answer
In the lanthanide series, +3 oxidation state is most common i.e., Ln(III) compounds are predominant. However, +2 and +4 oxidation states can also be found in the solution or in solid compounds.
8.11 Explain giving reasons:
(i) Transition metals and many of their compounds show paramagnetic behaviour.
(ii) The enthalpies of atomisation of the transition metals are high.
(iii) The transition metals generally form coloured compounds.
(iv) Transition metals and their many compounds act as good catalyst.
Show Answer
Answer
(i) Transition metals show paramagnetic behaviour. Paramagnetism arises due to the presence of unpaired electrons with each electron having a magnetic moment associated with its spin angular momentum and orbital angular momentum. However, in the first transition series, the orbital angular momentum is quenched. Therefore, the resulting paramagnetism is only because of the unpaired electron.
(ii) Transition elements have high effective nuclear charge and a large number of valence electrons. Therefore, they form very strong metallic bonds. As a result, the enthalpy of atomization of transition metals is high.
(iii) Most of the complexes of transition metals are coloured. This is because of the absorption of radiation from visible light region to promote an electron from one of the $d$-orbitals to another. In the presence of ligands, the $d$ orbitals split up into two sets of orbitals having different energies. Therefore, the transition of electrons can take place from one set toanother. The energy required for these transitions is quite small and falls in the visible region of radiation. The ions of transition metals absorb the radiation of a particular wavelength and the rest is reflected, imparting colour to the solution.
(iv) The catalytic activity of the transition elements can be explained by two basic facts.
(a) Owing to their ability to show variable oxidation states and form complexes, transition metals form unstable intermediate compounds. Thus, they provide a new path with lower activation energy, $E_{\mathrm{a}}$, for the reaction.
(b) Transition metals also provide a suitable surface for the reactions to occur.
8.12 What are interstitial compounds? Why are such compounds well known for transition metals?
Show Answer
Answer
Transition metals are large in size and contain lots of interstitial sites. Transition elements can trap atoms of other elements (that have small atomic size), such as H, C, N, in the interstitial sites of their crystal lattices. The resulting compounds are called interstitial compounds.
8.13 How is the variability in oxidation states of transition metals different from that of the non-transition metals? Illustrate with examples.
Show Answer
Answer
In transition elements, the oxidation state can vary from +1 to the highest oxidation state by removing all its valence electrons. Also, in transition elements, the oxidation states differ by $1\left(\mathrm{Fe}^{2+}\right.$ and $\mathrm{Fe}^{3+} ; \mathrm{Cu}^{+}$ and $\left.\mathrm{Cu}^{2+}\right)$. In non-transition elements, the oxidation states differ by 2 , for example, +2 and +4 or +3 and +5 , etc.
8.14 Describe the preparation of potassium dichromate from iron chromite ore. What is the effect of increasing $\mathrm{pH}$ on a solution of potassium dichromate?
Show Answer
Answer
(i) Preparation of $\mathrm{K}_2 \mathrm{Cr}_2 \mathrm{O}_7$ from chromite ore
(a) Potassium dichromate is obtained by the fusion of chromite ore $\left(\mathrm{FeCr}_2 \mathrm{O}_4\right)$ with sodium (or potassium) carbonate in the presence of excess air.
$ 4 \mathrm{FeCr}_2 \mathrm{O}_4+8 \mathrm{Na}_2 \mathrm{CO}_3+7 \mathrm{O}_2 \rightarrow \underset{\left(\substack{ \text{Yellow} \\ \text{solution} }\right)}{8 \mathrm{Na}_2 \mathrm{CrO}_4}+2 \mathrm{Fe}_2 \mathrm{O}_3+8 \mathrm{CO}_2 $
(b) The solution is filtered and treated with sulphuric acid.
$ 2 \mathrm{Na}_2 \mathrm{CrO}_4+\underset{\left(\mathrm{From} \mathrm{H}_2 \mathrm{SO}_4\right)}{2 \mathrm{H}^{+}} \rightarrow \underset{\substack{\text{Sodium}\\ \substack{\text{dichromate}\\ \text{(orange)}}}}{\mathrm{Na}_2 \mathrm{Cr}_2 \mathrm{O}_7(\mathrm{~s})}+2 \mathrm{Na}^{+}+\mathrm{H}_2 \mathrm{O} $
(c) Now sodium dichromate is treated with potassium chloride.
As a result, potassium dichromate is produced.
$ \mathrm{Na}_2 \mathrm{Cr}_2 \mathrm{O}_7+2 \mathrm{KCl} \rightarrow \underset{\substack{\text { Potassium } \\ \text { dichromate } \\ \text { crystals }}}{\mathrm{K}_2 \mathrm{Cr}_2 \mathrm{O}_7} +2 \mathrm{NaCl} $
(ii) Effect of increasing $\mathrm{pH}$ on $\mathrm{K}_2 \mathrm{Cr}_2 \mathrm{O}_7$ solution
$ \underset{\text { Orange }}{\mathrm{Cr}_2 \mathrm{O}_7^{2-}}+2 \mathrm{OH}^{-} \rightarrow \underset{\text { Yellow }}{2 \mathrm{CrO}_4^{2-}}+\mathrm{H}_2 \mathrm{O} $
On increasing $\mathrm{pH} ; \mathrm{K}_2 \mathrm{Cr}_2 \mathrm{O}_7$ changes into $\mathrm{K}_2 \mathrm{CrO}_4$ (orange to yellow).
8.15 Describe the oxidising action of potassium dichromate and write the ionicequations for its reaction with:
(i) iodide
(ii) iron(II) solution and
(iii) $\mathrm{H_2} \mathrm{~S}$
Show Answer
Answer
$\mathrm{K_2} \mathrm{Cr_2} \mathrm{O_7}$ acts as a very strong oxidising agent in the acidic medium.
$\mathrm{K_2} \mathrm{Cr_2} \mathrm{O_7}+4 \mathrm{H_2} \mathrm{SO_4} \longrightarrow \mathrm{K_2} \mathrm{SO_4}+\mathrm{Cr_2}\left(\mathrm{SO_4}\right)_{3}+4 \mathrm{H_2} \mathrm{O}+3[\mathrm{O}]$
$\mathrm{K_2} \mathrm{Cr_2} \mathrm{O_7}$ takes up electrons to get reduced and acts as an oxidising agent. The reaction of $\mathrm{K_2} \mathrm{Cr_2} \mathrm{O_7}$ with other iodide, iron (II) solution, and $\mathrm{H_2} \mathrm{~S}$ are given below.
(i) $\mathrm{K_2} \mathrm{Cr_2} \mathrm{O_7}$ oxidizes iodide to iodine.
$ \begin{aligned} \mathrm{Cr}_2 \mathrm{O}_7^{2-}+14 \mathrm{H}^{+}+6 \mathrm{e}^{-} & \longrightarrow 2 \mathrm{Cr}^{3+}+7 \mathrm{H}_2 \mathrm{O} \\ 2 \mathrm{I}^{-} & \left.\longrightarrow \mathrm{I}_2+2 \mathrm{e}^{-}\right] \times 3 \\ \hline \mathrm{Cr}_2 \mathrm{O}_7^{2-}+6 \mathrm{I}^{-}+14 \mathrm{H}^{+} & \longrightarrow 2 \mathrm{Cr}^{3+}+3 \mathrm{I}_2+7 \mathrm{H}_2 \mathrm{O} \\ \hline \end{aligned} $
(ii) $\mathrm{K_2} \mathrm{Cr_2} \mathrm{O_7}$ oxidizes iron (II) solution to iron (III) solution i.e., ferrous ions to ferric ions.
$ \begin{aligned} \mathrm{Cr_2} \mathrm{O_7}^{2-}+14 \mathrm{H}^{+}+6 \mathrm{e}^{-} & \longrightarrow 2 \mathrm{Cr}^{3+}+7 \mathrm{H_2} \mathrm{O} \\ \mathrm{Fe}^{2+} & \left.\longrightarrow \mathrm{Fe}^{3+}+\mathrm{e}^{-}\right] \times 6 \\ \hline \mathrm{Cr_2} \mathrm{O_7}^{2-}+14 \mathrm{H}^{+}+6 \mathrm{Fe}^{2+} & \longrightarrow 2 \mathrm{Cr}^{3+}+6 \mathrm{Fe}^{3+}+7 \mathrm{H_2} \mathrm{O} \\ \hline \end{aligned} $
(iii) $\mathrm{K_2} \mathrm{Cr_2} \mathrm{O_7}$ oxidizes $\mathrm{H_2} \mathrm{~S}$ to sulphur.
$ \begin{aligned} \mathrm{Cr_2} \mathrm{O_7}^{2-}+14 \mathrm{H}^{+}+6 \mathrm{e}^{-} & \longrightarrow 2 \mathrm{Cr}^{3+}+7 \mathrm{H_2} \mathrm{O} \\ \mathrm{H_2} \mathrm{~S} & \left.\longrightarrow \mathrm{S}+2 \mathrm{H}^{+}+2 \mathrm{e}^{-}\right] \times 3 \\ \hline \mathrm{Cr_2} \mathrm{O_7}^{2-}+3 \mathrm{H_2} \mathrm{~S}+8 \mathrm{H}^{+} & \longrightarrow 2 \mathrm{Cr}^{3+}+3 \mathrm{~S}+7 \mathrm{H_2} \mathrm{O} \\ \hline \end{aligned} $
8.16 Describe the preparation of potassium permanganate. How does the acidifiedpermanganate solution react with (i) iron(II) ions (ii) $\mathrm{SO_2}$ and (iii) oxalic acid? Write the ionic equations for the reactions.
Show Answer
Answer
Potassium permanganate can be prepared from pyrolusite $\left(\mathrm{MnO_2}\right)$. The ore is fused with $\mathrm{KOH}$ in the presence of either atmospheric oxygen or an oxidising agent, such as $\mathrm{KNO_3}$ or $\mathrm{KClO_4}$, to give $\mathrm{K_2} \mathrm{MnO_4}$.
$ 2 \mathrm{MnO_2}+4 \mathrm{KOH}+\mathrm{O_2} \xrightarrow{\text { heat }} {\text{(Green)}}{2 \mathrm{~K_2} \mathrm{MnO_4}}+2 \mathrm{H_2} \mathrm{O} $
The green mass can be extracted with water and then oxidized either electrolytically or by passing chlorine/ozone into the solution.
Electrolytic oxidation
$ \begin{aligned} & \mathrm{K_2} \mathrm{MnO_4} \longleftrightarrow 2 \mathrm{~K}^{+}+\mathrm{MnO_4}^{2-} \\ & \mathrm{H_2} \mathrm{O} \longleftrightarrow \mathrm{H}^{+}+\mathrm{OH}^{-} \end{aligned} $
At anode, manganate ions are oxidized to permanganate ions.
$ \underset{\text{Green}}{\mathrm{MnO_4}^{2-}} \longleftrightarrow \underset{\text{Green}}{\mathrm{MnO_4}^{-}}+\mathrm{e}^{-} $
Oxidation by chlorine
$ \begin{aligned} & 2 \mathrm{~K_2} \mathrm{MnO_4}+\mathrm{Cl_2} \longrightarrow 2 \mathrm{KMnO_4}+2 \mathrm{KCl} \\ & 2 \mathrm{MnO_4}^{2-}+\mathrm{Cl_2} \longrightarrow 2 \mathrm{MnO_4}^{-}+2 \mathrm{Cl}^{-} \end{aligned} $
Oxidation by ozone
$ \begin{aligned} 2 \mathrm{~K_2} \mathrm{MnO_4}+\mathrm{O_3}+\mathrm{H_2} \mathrm{O} \longrightarrow 2 \mathrm{KMnO_4}+2 \mathrm{KOH}+\mathrm{O_2} \\ 2 \mathrm{MnO_4}^{2-}+\mathrm{O_3}+\mathrm{H_2} \mathrm{O} \longrightarrow 2 \mathrm{MnO_4}^{2-}+2 \mathrm{OH}^{-}+\mathrm{O_2} \end{aligned} $
(i) Acidified $\mathrm{KMnO_4}$ solution oxidizes $\mathrm{Fe}$ (II) ions to $\mathrm{Fe}$ (III) ions i.e., ferrous ions to ferric ions.
$ \begin{aligned} \mathrm{MnO_4}^{-}+8 \mathrm{H}^{+}+5 \mathrm{e}^{-} & \longrightarrow \mathrm{Mn}^{2+}+4 \mathrm{H_2} \mathrm{O} \\ \mathrm{Fe}^{2+} & \longrightarrow \mathrm{Fe}^{3+}+\mathrm{e}^{-} ] \times 5 \\ \hline \mathrm{MnO_4}^{-}+5 \mathrm{Fe}^{2+}+8 \mathrm{H}^{+} & \longrightarrow \mathrm{Mn}^{2+}+5 \mathrm{Fe}^{3+}+4 \mathrm{H_2} \mathrm{O} \\ \hline \end{aligned} $
(ii) Acidified potassium permanganate oxidizes $\mathrm{SO_2}$ to sulphuric acid.
$ \begin{aligned} & \mathrm{MnO_4}^{-}+6 \mathrm{H}^{+}+5 \mathrm{e}^{-}\left.\longrightarrow \mathrm{Mn}^{2+}+3 \mathrm{H_2} \mathrm{O}\right] \times 2 \\ & 2 \mathrm{H_2} \mathrm{O}+2 \mathrm{SO_2}+\mathrm{O_2}\left.\longrightarrow 4 \mathrm{H}^{+}+2 \mathrm{SO_4}^{2-}+2 \mathrm{e}^{-}\right] \times 5 \\ \hline & 2 \mathrm{MnO_4}^{-}+10 \mathrm{SO_2}+5 \mathrm{O_2}+4 \mathrm{H_2} \mathrm{O} \longrightarrow 2 \mathrm{Mn}^{2+}+10 \mathrm{SO_4}^{2-}+8 \mathrm{H}^{+}\\ \hline \end{aligned} $
(iii) Acidified potassium permanganate oxidizes oxalic acid to carbon dioxide.
$ \begin{aligned} \mathrm{MnO _4}^{-}+8 \mathrm{H}^{+}+5 \mathrm{e}^{-} & \longrightarrow \mathrm{Mn}^{2+}+4 \mathrm{H_2} \mathrm{O}] \times 2 \\ \mathrm{C _2} \mathrm{O_4}^{2-} & \longrightarrow 2 \mathrm{CO _2}+2 \mathrm{e}^{-}] \times 5 \\ \hline 2 \mathrm{MnO _4}^{-}+5 \mathrm{C _2} \mathrm{O_4}^{2-}+16 \mathrm{H}^{+} & \longrightarrow 2 \mathrm{Mn}^{2+}+10 \mathrm{CO _2}+8 \mathrm{H _2} \mathrm{O} \\ \hline \end{aligned} $
8.17 For $\mathrm{M}^{2+} / \mathrm{M}$ and $\mathrm{M}^{3+} / \mathrm{M}^{2+}$ systems, the $\mathrm{E}^{\ominus}$ values for some metals are as follows:
| $\mathrm{Cr}^{2+} / \mathrm{Cr}$ | $-0.9 \mathrm{~V}$ | $\mathrm{Cr}^{3} / \mathrm{Cr}^{2+}$ | $-0.4 \mathrm{~V}$ |
|---|---|---|---|
| $\mathrm{Mn}^{2+} / \mathrm{Mn}$ | $-1.2 \mathrm{~V}$ | $\mathrm{Mn}^{3+} / \mathrm{Mn}^{2+}$ | $+1.5 \mathrm{~V}$ |
| $\mathrm{Fe}^{2+} / \mathrm{Fe}$ | $-0.4 \mathrm{~V}$ | $\mathrm{Fe}^{3+} / \mathrm{Fe}^{2+}$ | $+0.8 \mathrm{~V}$ |
Use this data to comment upon:
(i) The stability of $\mathrm{Fe}^{3+}$ in acid solution as compared to that of $\mathrm{Cr}^{3+} \mathrm{or} \mathrm{Mn}^{3+}$ and
(ii) The ease with which iron can be oxidised as compared to a similar process for either chromium or manganese metal.
Show Answer
Answer
(i) The $\mathrm{E}^{\ominus}$ value for $\mathrm{Fe}^{3+} / \mathrm{Fe}^{2+}$ is higher than that for $\mathrm{Cr}^{3+} / \mathrm{Cr}^{2+}$ and lower than that for $\mathrm{Mn}^{3+} / \mathrm{Mn}^{2+}$. So, the reduction of $\mathrm{Fe}^{3+}$ to $\mathrm{Fe}^{2+}$ is easier than the reduction of $\mathrm{Mn}^{3+}$ to $\mathrm{Mn}^{2+}$, but not as easy as the reduction of $\mathrm{Cr}^{3+}$ to $\mathrm{Cr}^{2+}$. Hence, $\mathrm{Fe}^{3+i}$ is more stable than $\mathrm{Mn}^{3+}$, but less stable than $\mathrm{Cr}^{3+}$. These metal ions can be arranged in the increasing order of their stability as: $\mathrm{Mn}^{3+}<\mathrm{Fe}^{3+}<\mathrm{Cr}^{3+}$
(ii) The reduction potentials for the given pairs increase in the following order.
$\mathrm{Mn}^{2+} / \mathrm{Mn}<\mathrm{Cr}^{2+} / \mathrm{Cr}<\mathrm{Fe}^{2+} / \mathrm{Fe}$
So, the oxidation of $\mathrm{Fe}$ to $\mathrm{Fe}^{2+}$ is not as easy as the oxidation of $\mathrm{Cr}$ to $\mathrm{Cr}^{2+}$ and the oxidation of $\mathrm{Mn}$ to $\mathrm{Mn}^{2+}$. Thus, these metals can be arranged in the increasing order of their ability to get oxidised as: $\mathrm{Fe}<\mathrm{Cr}<\mathrm{Mn}$
8.18 Predict which of the following will be coloured in aqueous solution? $\mathrm{Ti}^{3+}, \mathrm{V}^{3+}$, $\mathrm{Cu}^{+}, \mathrm{Sc}^{3+}, \mathrm{Mn}^{2+}, \mathrm{Fe}^{3+}$ and $\mathrm{Co}^{2+}$. Give reasons for each.
Show Answer
Answer
Only the ions that have electrons in $d$-orbital and in which $d$-d transition is possible will be coloured. The ions in which $d$-orbitals are empty or completely filled will be colourless as no $d$-d transition is possible in those configurations.
| Element | Atomic Number | Ionic State | Electronic configuration in ionic state |
|---|---|---|---|
| $\mathrm{Ti}$ | 22 | $\mathrm{T1}^{3+}$ | $[\mathrm{Ar}] 3 d^{1}$ |
| $\mathrm{V}$ | 23 | $\mathrm{~V}^{3+}$ | $[\mathrm{Ar}] 3 d^{2}$ |
| $\mathrm{Cu}$ | 29 | $\mathrm{Cu}^{+}$ | $[\mathrm{Ar}] 3 d^{10}$ |
| $\mathrm{Sc}$ | 21 | $\mathrm{Sc}^{3+}$ | $[\mathrm{Ar}]$ |
| $\mathrm{Mn}$ | 25 | $\mathrm{Mn}^{2+}$ | $[\mathrm{Ar}] 3 d^{5}$ |
| $\mathrm{Fe}$ | 26 | $\mathrm{Fe}^{3+}$ | $[\mathrm{Ar}] 3 d^{5}$ |
| $\mathrm{Co}$ | 27 | $\mathrm{Co}^{2+}$ | $[\mathrm{Ar}] 3 d^{7}$ |
From the above table, it can be easily observed that only $\mathrm{Sc}^{3+}$ has an empty $d$-orbital and $\mathrm{Cu}^{+}$has completely filled $\mathrm{d}$ orbitals. All other ions, except $\mathrm{Sc}^{3+}$ and $\mathrm{Cu}^{+}$, will be coloured in aqueous solution because of $d$ - $d$ transitions.
8.19 Compare the stability of +2 oxidation state for the elements of the first transition series.
Show Answer
Answer
$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline \text{Sc} & & & +3 & & & \\ \hline \mathrm{Ti} & +1 & +2 & +3 & +4 & & \\ \hline \mathrm{V} & +1 & +2 & +3 & +4 & +5 & \\ \hline \mathrm{Cr} & +1 & +2 & +3 & +4 & +5 & +6 \\ \hline \mathrm{Mn} & +1 & +2 & +3 & +4 & +5 & +6 & +7 \\ \hline \mathrm{Fe} & +1 & +2 & +3 & +4 & +5 & +6 & \\ \hline \mathrm{Co} & +1 & +2 & +3 & +4 & +5 & & \\ \hline \mathrm{Ni} & +1 & +2 & +3 & +4 & & & \\ \hline \mathrm{Cu} & +1 & +2 & +3 & & & & \\ \hline \mathrm{Zn} & & +2 & & & & & \\ \hline \end{array} $
From the above table, it is evident that the maximum number of oxidation states is shown by $\mathrm{Mn}$, varying from +2 to +7. The number of oxidation states increases on moving from Sc to Mn. On moving from Mn to Zn, the number of oxidation states decreases due to a decrease in the number of available unpaired electrons. The relative stability of the +2 oxidation state increases on moving from top to bottom. This is because on moving from top to bottom, it becomes more and more difficult to remove the third electron from the $d$-orbital.
8.20 Compare the chemistry of actinoids with that of the lanthanoids with specialreference to:
(i) electronic configuration
(iii) oxidation state
(ii) atomic and ionic sizes and
(iv) chemical reactivity.
Show Answer
Answer
(i) Electronic configuration
The general electronic configuration for lanthanoids is $[\mathrm{Xe}]^{54} 4 f^{0-14} 5 d^{0-1} 6 s^{2}$ and that for actinoids is $[\mathrm{Rn}]^{86} 5 f^{-14} 6 d^{0-1} 7 s^{2}$. Unlike 4 forbitals, $5 f$ orbitals are not deeply buried and participate in bonding to a greater extent.
(ii) Oxidation states
The principal oxidation state of lanthanoids is (+3). However, sometimes we also encounter oxidation states of +2 and +4 . This is because of extra stability of fully-filled and half-filled orbitals. Actinoids exhibit a greater range of oxidation states. This is because the $5 f, 6 d$, and 7 slevels are of comparable energies. Again, (+3) is the principal oxidation state for actinoids. Actinoids such as lanthanoids have more compounds in +3 state than in +4 state.
(iii) Atomic and lonic sizes
Similar to lanthanoids, actinoids also exhibit actinoid contraction (overall decrease in atomic and ionic radii). The contraction is greater due to the poor shielding effect of 5 forbitals.
(iv) Chemical reactivity
In the lanthanide series, the earlier members of the series are more reactive. They have reactivity that is comparable to $\mathrm{Ca}$. With an increase in the atomic number, the lanthanides start behaving similar to Al. Actinoids, on the other hand, are highly reactive metals, especially when they are finely divided. When they are added to boiling water, they give a mixture of oxide and hydride. Actinoids combine with most of the non-metals at moderate temperatures. Alkalies have no action on these actinoids. In case of acids, they are slightly affected by nitric acid (because of the formation of a protective oxide layer).
8.21 How would you account for the following:
(i) Of the $d^{4}$ species, $\mathrm{Cr}^{2+}$ is strongly reducing while manganese(III) is strongly oxidising.
(ii) Cobalt(II) is stable in aqueous solution but in the presence of complexing reagents it is easily oxidised.
(iii) The $d^{1}$ configuration is very unstable in ions.
Show Answer
Answer
(i) $\mathrm{Cr}^{2+}$ is strongly reducing in nature. It has a $d^{4} c$ configuration. While acting as a reducing agent, it gets oxidized to
$\mathrm{Cr}^{3+}\left(\right.$ electronic configuration, $\left.d^{\beta}\right)$. This $d^{3}$ configuration can be written as $t_{2 \mathrm{~g}}^{3}$ configuration, which is a more stable configuration. In the case of $\mathrm{Mn}^{3+}\left(d^{4}\right)$, it acts as an oxidizing agent and gets reduced to $\mathrm{Mn}^{2+}\left(d^{5}\right)$. This has an exactly half-filled $d$-orbital and is highly stable.
(ii) $\mathrm{Co}(\mathrm{II})$ is stable in aqueous solutions. However, in the presence of strong field complexing reagents, it is oxidized to Co (III). Although the 3rionization energy for Co is high, but the higher amount of crystal field stabilization energy (CFSE) released in the presence of strong field ligands overcomes this ionization energy.
(iii) The ions in $d^{11}$ configuration tend to lose one more electron to get into stable $d^{0}$ configuration. Also, the hydration or lattice energy is more than sufficient to remove the only electron present in the $d$-orbital of these ions. Therefore, they act as reducing agents.
8.22 What is meant by ‘disproportionation’? Give two examples of disproportionation reaction in aqueous solution.
Show Answer
Answer
It is found that sometimes a relatively less stable oxidation state undergoes an oxidation - reduction reaction in which it is simultaneously oxidised and reduced. This is called disproportionation.
Forexample,
(i) $\underset{\mathrm{Cr(V)}}{\mathrm{3CrO_{4}^{3-}}} + \mathrm{8H^+} \longrightarrow \underset{\mathrm{Cr(VI)}}{\mathrm{3CrO_{4}^{2-}}} + \underset{\mathrm{Cr(III)}}{\mathrm{CrO^{3+}}} + \mathrm{4H_2O} $
$\mathrm{Cr}(\mathrm{V})$ is oxidized to $\mathrm{Cr}(\mathrm{VI})$ and reduced to $\mathrm{Cr}(\mathrm{III})$.
(ii) $\underset{\mathrm{Mn(VI)}}{3 \mathrm{MnO_{4}^{2-}}}+4 \mathrm{H}^{+} \longrightarrow \underset{\mathrm{Mn(VII)}}{2 \mathrm{MnO_{4}^{-}}}+\underset{\mathrm{Mn(IV)}}{\mathrm{MnO_2}}+2 \mathrm{H_2} \mathrm{O}$
$\mathrm{Mn}(\mathrm{VI})$ is oxidized to $\mathrm{Mn}(\mathrm{VII})$ and reduced to Mn (IV).
8.23 Which metal in the first series of transition metals exhibits +1 oxidationstate most frequently and why?
Show Answer
Answer
In the first transition series, Cu exhibits +1 oxidation state very frequently. It is because $\mathrm{Cu}(+1)$ has an electronic configuration of $[\mathrm{Ar}] 3 d^{10}$. The completely filled $d$-orbital makes it highly stable.
8.24 Calculate the number of unpaired electrons in the following gaseous ions: $\mathrm{Mn}^{3+}, \mathrm{Cr}^{3+}, \mathrm{V}^{3+}$ and $\mathrm{Ti}^{3+}$. Which one of these is the most stable in aqueous solution?
Show Answer
Answer
| Gaseous ions | Number of unpaired electrons | |
|---|---|---|
| (i) | $\mathrm{Mn}^{3+},[\mathrm{Ar}] 3 d^{4}$ | 4 |
| (ii) | $\mathrm{Cr}^{3+},[\mathrm{Ar}] 3 d^{3}$ | 3 |
| (iii) | $\mathrm{V}^{3+},[\mathrm{Ar}] 3 d^{2}$ | 2 |
| (vi) | $\mathrm{Ti}^{3+},[\mathrm{Ar}] 3 d^{1}$ | 1 |
$\mathrm{Cr}^{3+}$ is the most stable in aqueous solutions owing to a $t_{2 \mathrm{~g}}^{3}$ configuration.
8.25 Give examples and suggest reasons for the following features of the transition metal chemistry:
(i)The lowest oxide of transition metal is basic, the highest is amphoteric/acidic.
(ii)A transition metal exhibits highest oxidation state in oxides and fluorides.
(iii) The highest oxidation state is exhibited in oxoanions of a metal.
Show Answer
Answer
(i) In the case of a lower oxide of a transition metal, the metal atom has a low oxidation state. This means that some of the valence electrons of the metal atom are not involved in bonding. As a result, it can donate electrons and behave as a base.
On the other hand, in the case of a higher oxide of a transition metal, the metal atom has a high oxidation state. This means that the valence electrons are involved in bonding and so, they are unavailable. There is also a high effective nuclear charge.
As a result, it can accept electrons and behave as an acid.
For example, $\mathrm{Mn}^{\mathrm{II}} \mathrm{O_\text {is basic and }} \mathrm{Mn_2} \mathrm{O_7}$ is acidic.
(ii) Oxygen and fluorine act as strong oxidising agents because of their high electronegativities and small sizes. Hence, they bring out the highest oxidation states from the transition metals. In other words, a transition metal exhibits higher oxidation states in oxides and fluorides. For example, in $\mathrm{OsF_6}$ and $\mathrm{V_2} \mathrm{O_5}$, the oxidation states of $\mathrm{Os}$ and V are +6 and +5 respectively.
(iii) Oxygen is a strong oxidising agent due to its high electronegativity and small size. So, oxo-anions of a metal have the highest oxidation state. For example, in $\mathrm{MnO_4}^{-}$, the oxidation state of $\mathrm{Mn}$ is +7 .
8.26 Indicate the steps in the preparation of:
(i) $\mathrm{K} 2 \mathrm{Cr} 2 \mathrm{O} 7$ from chromite ore.
(ii) $\mathrm{KMnO4}$ from pyrolusite ore.
Show Answer
Answer
(i)
Potassium dichromate $\left(\mathrm{K_2} \mathrm{Cr_2} \mathrm{O_7}\right)$ is prepared from chromite ore $\left(\mathrm{FeCr_2} \mathrm{O_4}\right)$ in the following steps.
Step (1):Preparation of sodium chromate
$ 4 \mathrm{FeCr_2} \mathrm{O_4}+16 \mathrm{NaOH}+7 \mathrm{O_2} \longrightarrow 8 \mathrm{Na_2} \mathrm{CrO_4}+2 \mathrm{Fe_2} \mathrm{O_3}+8 \mathrm{H_2} \mathrm{O} $
Step (2):Conversion of sodium chromate into sodium dichromate
$ 2 \mathrm{Na_2} \mathrm{CrO_4}+\text { conc. } \mathrm{H_2} \mathrm{SO_4} \longrightarrow \mathrm{Na_2} \mathrm{Cr_2} \mathrm{O_7}+\mathrm{Na_2} \mathrm{SO_4}+\mathrm{H_2} \mathrm{O} $
Step(3):Conversion of sodium dichromate to potassium dichromate
$ \mathrm{Na_2} \mathrm{Cr_2} \mathrm{O_7}+2 \mathrm{KCl} \longrightarrow \mathrm{K_2} \mathrm{Cr_2} \mathrm{O_7}+2 \mathrm{NaCl} $
Potassium chloride being less soluble than sodium chloride is obtained in the form of orange coloured crystals and can be removed by filtration.
$ \underset{\substack{\text{Chromate}\\ \text{(Yellow)}}}{2 \mathrm{CrO_{4}^{2-}}} \stackrel{\text{Acid}}{\underset{\text{Alkali}}{\leftarrow\rightarrow}} \underset{\substack{\text{Hydrogen} \\ \text{(Chromate)}}}{2 \mathrm{HCrO_{4}^{-}}}\stackrel{\text{Acid}}{\underset{\text{Alkali}}{\leftarrow\rightarrow}} \underset{\substack{\text{Dichromate}\\ \text{(Orange)}}}{\mathrm{Cr_2} \mathrm{O_7}^{2-}} $
The dichromate ion $\left(\mathrm{Cr_2} \mathrm{O_7}^{2-}\right)$ exists in equilibrium with chromate $\left(\mathrm{CrO_4}^{2-}\right)$ ion at $\mathrm{pH} 4$. However, by changing the $\mathrm{pH}$, they can be interconverted. (ii)
Potassium permanganate $\left(\mathrm{KMnO_4}\right.$ ) can be prepared from pyrolusite $\left(\mathrm{MnO_2}\right)$. The ore is fused with $\mathrm{KOH}$ in the presence of either atmospheric oxygen or an oxidising agent, such as $\mathrm{KNO_3} \mathrm{Or} \mathrm{KClO_4}$, to give $\mathrm{K_2} \mathrm{MnO_4}$.
$ 2 \mathrm{MnO_2}+4 \mathrm{KOH}+\mathrm{O_2} \xrightarrow{\text { heat }} \underset{\text{(Green)}}{2 \mathrm{~K_2} \mathrm{MnO_4}}+2 \mathrm{H_2} \mathrm{O} $
The green mass can be extracted with water and then oxidized either electrolytically or by passing chlorine/ozone into the solution.
Electrolytic oxidation
$ \begin{aligned} & \mathrm{K_2} \mathrm{MnO_4} \longleftrightarrow 2 \mathrm{~K}^{+}+\mathrm{MnO_4}^{2-} \\ & \mathrm{H_2} \mathrm{O} \longleftrightarrow \mathrm{H}^{+}+\mathrm{OH}^{-} \end{aligned} $
At anode, manganate ions are oxidized to permanganate ions.
$ \underset{\text{Green}}{\mathrm{MnO_4}^{2-}} \longleftrightarrow \underset{\text{Purple}}{\mathrm{MnO_4}^{-}}+\mathrm{e}^{-} $
Green Purple
Oxidation by chlorine
$ \begin{aligned} & 2 \mathrm{~K_2} \mathrm{MnO_4}+\mathrm{Cl_2} \longrightarrow 2 \mathrm{KMnO_4}+2 \mathrm{KCl} \\ & 2 \mathrm{MnO_4}^{2-}+\mathrm{Cl_2} \longrightarrow 2 \mathrm{MnO_4}^{-}+2 \mathrm{Cl}^{-} \end{aligned} $
Oxidation by ozone
$ \begin{aligned} & 2 \mathrm{~K_2} \mathrm{MnO_4}+\mathrm{O_3}+\mathrm{H_2} \mathrm{O} \longrightarrow 2 \mathrm{KMnO_4}+2 \mathrm{KOH}+\mathrm{O_2} \\ & 2 \mathrm{MnO_4}^{2-}+\mathrm{O_3}+\mathrm{H_2} \mathrm{O} \longrightarrow 2 \mathrm{MnO_4}^{2-}+2 \mathrm{OH}^{-}+\mathrm{O_2} \end{aligned} $
8.27 What are alloys? Name an important alloy which contains some of thelanthanoid metals. Mention its uses.
Show Answer
Answer
An alloy is a solid solution of two or more elements in a metallic matrix. It can either be a partial solid solution or a complete solid solution. Alloys are usually found to possess different physical properties than those of the component elements.
An important alloy of lanthanoids is Mischmetal. It contains lanthanoids (94-95 $\%$), iron (5 $\%$), and traces of S, C, Si, $\mathrm{Ca}$, and $\mathrm{Al}$.
Uses
(1) Mischmetal is used in cigarettes and gas lighters.
(2) It is used in flame throwing tanks.
(3) It is used in tracer bullets and shells.
8.28 What are inner transition elements? Decide which of the following atomic numbers are the atomic numbers of the inner transition elements: 29, 59, 74, 95, 102, 104.
Show Answer
Answer
Inner transition metals are those elements in which the last electron enters the $f$-orbital. The elements in which the $4 f$ and the $5 f$ orbitals are progressively filled are called $f$-block elements. Among the given atomic numbers, the atomic numbers of the inner transition elements are 59, 95, and 102.
8.29 The chemistry of the actinoid elements is not so smooth as that of the Lanthanoids. Justify this statement by giving some examples from the oxidation state of these elements.
Show Answer
Answer
Lanthanoids primarily show three oxidation states (+2,+3,+4). Among these oxidation states, +3 state is the most common. Lanthanoids display a limited number of oxidation states because the energy difference between $4 f, 5 d$, and 6 sorbitals is quite large. On the other hand, the energy difference between $5 f, 6 d$, and $7 s$ orbitals is very less. Hence, actinoids display a large number of oxidation states. For example, uranium and plutonium display +3,+4,+5, and +6 oxidation states while neptunium displays +3,+4,+5, and +7 . The most common oxidation state in case of actinoids is also +3 .
8.30 Which is the last element in the series of the actinoids? Write the electronic configuration of this element. Comment on the possible oxidation state of this element.
Show Answer
Answer
The last element in the actinoid series is lawrencium, Lr. Its atomic number is 103 and its electronic configuration is $[\operatorname{Rn}] 5 f^{14} 6 d^{1} 7 s^{2}$. The most common oxidation state displayed by it is +3 ; because after losing 3 electrons it attains stablef ${ }^{14}$ configuration.
8.31 Use Hund’s rule to derive the electronic configuration of $\mathrm{Ce}^{3+}$ ion and calculate its magnetic moment on the basis of ‘spin-only’ formula.
Show Answer
Answer
Ce : $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10} 4 s^{2} 4 p^{6} 4 d^{10} 5 s^{2} 5 p^{6} 4 f^{1} 5 d^{1} 6 s^{2}$
Magnetic moment can be calculated as:
$\mu=\sqrt{n(n+2)}$
Where,
$n=$ number of unpaired electrons
The electronic configuration of $\mathrm{Ce}^{3+}: 1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10} 4 s^{2} 4 p^{6} 4 d^{10} 5 s^{2} 5 p^{6} 4 f^{1}$
In $\mathrm{Ce}^{3+}, n=1$
$\therefore$ Magnetic moment, $\mu=\sqrt{\mathrm{n}(\mathrm{n}+2)}$ B.M
$ \begin{aligned} & \Longrightarrow \mu=\sqrt{1(1+2)} \text { B.M } \\ & \Longrightarrow \mu=\sqrt{3} \text { B.M } \\ & \Longrightarrow \mu=1.73 \text { B.M } \end{aligned} $
8.32 Name the members of the lanthanoid series which exhibit +4 oxidation state and those which exhibit +2 oxidation state. Try to correlate this type of behavior with the electronic configurations of these elements.
Show Answer
Answer
The lanthanides that exhibit +2 and +4 states are shown in the given table. The atomic numbers of the elements are given in the parenthesis.
| $\mathbf{+ 2}$ | $\mathbf{+ 4}$ |
|---|---|
| $\mathrm{Nd}(60)$ | $\mathrm{Ce}(58)$ |
| $\mathrm{Sm}(62)$ | $\operatorname{Pr}(59)$ |
| $\operatorname{Eu}(63)$ | $\mathrm{Nd}(60)$ |
| $\mathrm{Tm}(69)$ | $\mathrm{Tb}(65)$ |
| $\mathrm{Yb}(70)$ | $\mathrm{Dy}(66)$ |
Ce after forming $\mathrm{Ce}^{4+}$ attains a stable electronic configuration of $[\mathrm{Xe}]$.
$\mathrm{Tb}$ after forming $\mathrm{Tb}^{4+}$ attains a stable electronic configuration of $[\mathrm{Xe}] 4 f$.
Eu after forming $\mathrm{Eu}^{2+}$ attains a stable electronic configuration of $[\mathrm{Xe}] 4 f^{\prime}$.
$\mathrm{Yb}$ after forming $\mathrm{Yb}^{2+}$ attains a stable electronic configuration of $[\mathrm{Xe}] 4 f^{44}$
8.33 Compare the chemistry of the actinoids with that of lanthanoids with reference to:
(i) electronic configuration
(ii) oxidation states and
(iii) chemical reactivity.
Show Answer
Answer
Electronic configuration
The general electronic configuration for lanthanoids is $[\mathrm{Xe}]^{54} 4 f^{0-14} 5 d^{0-1} 6 s^{2}$ and that for actinoids is $[\mathrm{Rn}]^{86} 5 f^{-14} 6 d^{0-1} 7 s^{2}$. Unlike 4 forbitals, $5 f$ orbitals are not deeply buried and participate in bonding to a greater extent.
Oxidation states
The principal oxidation state of lanthanoids is (+3). However, sometimes we also encounter oxidation states of +2 and +4 . This is because of extra stability of fully-filled and half-filled orbitals. Actinoids exhibit a greater range of oxidation states. This is because the $5 f, 6 d$, and 7 slevels are of comparable energies. Again, $(+3)$ is the principal oxidation state for actinoids. Actinoids such as lanthanoids have more compounds in +3 state than in +4 state.
Chemical reactivity
In the lanthanide series, the earlier members of the series are more reactive. They have reactivity that is comparable to Ca. With an increase in the atomic number, the lanthanides start behaving similar to Al. Actinoids, on the other hand, are highly reactive metals, especially when they are finely divided. When they are added to boiling water, they give a mixture of oxide and hydride. Actinoids combine with most of the non-metals at moderate temperatures. Alkalies have no action on these actinoids. In case of acids, they are slightly affected by nitric acid (because of the formation of a protective oxide layer).
8.34 Write the electronic configurations of the elements with the atomic numbers 61, 91, 101, and 109.
Show Answer
Answer
| Atomic number | Electronic configuration |
|---|---|
| 61 | $[\mathrm{Xe}]^{54} 4 f^{5} 5 d^{0} 6 s^{2}$ |
| 91 | $[\mathrm{Rn}]^{86} 5 f^{2} 6 d^{1} 7 s^{2}$ |
| 101 | $[\mathrm{Rn}]^{86} 5 f^{13} 5 d^{0} 7 s^{2}$ |
| 109 | $[\mathrm{Rn}]^{86} 5 f^{14} 6 d^{7} 7 s^{2}$ |
8.35 Compare the general characteristics of the first series of the transition metals with those of the second and third series metals in the respective vertical columns. Give special emphasis on the following points:
(i) electronic configurations,
(ii) oxidation states,
(iii) ionisation enthalpies, and
(iv) atomic sizes.
Show Answer
Answer
(i) In the $1^{\text {st }}, 2^{\text {nd }}$ and $3^{\text {rd }}$ transition series, the $3 d, 4 d$ and $5 d$ orbitals are respectively filled.
We know that elements in the same vertical column generally have similar electronic configurations.
In the first transition series, two elements show unusual electronic configurations:
$ \begin{aligned} & \operatorname{Cr}(24)=3 d^{5} 4 s^{1} \\ & \mathrm{Cu}(29)=3 d^{10} 4 s^{1} \end{aligned} $
Similarly, there are exceptions in the second transition series. These are:
$ \begin{aligned} & \mathrm{Mo}(42)=4 d^{5} 5 s^{1} \\ & \mathrm{Tc}(43)=4 d^{6} 5 s^{1} \\ & \mathrm{Ru}(44)=4 d^{7} 5 s^{1} \\ & \mathrm{Rh}(45)=4 d^{8} 5 s^{1} \\ & \mathrm{Pd}(46)=4 d^{10} 5 s^{0} \\ & \mathrm{Ag}(47)=4 d^{10} 5 s^{1} \end{aligned} $
There are some exceptions in the third transition series as well. These are:
$ \begin{aligned} & \mathrm{W}(74)=5 d^{4} 6 s^{2} \\ & \mathrm{Pt}(78)=5 d^{9} 6 s^{1} \\ & \mathrm{Au}(79)=5 d^{10} 6 s^{1} \end{aligned} $
As a result of these exceptions, it happens many times that the electronic configurations of the elements present in the same group are dissimilar.
(ii) In each of the three transition series the number of oxidation states shown by the elements is the maximum in the middle and the minimum at the extreme ends.
However, +2 and +3 oxidation states are quite stable for all elements present in the first transition series. All metals present in the first transition series form stable compounds in the +2 and +3 oxidation states. The stability of the +2 and +3 oxidation states decreases in the second and the third transition series, wherein higher oxidation states are more important.
For example $\left[\stackrel{\text{II}}{\mathrm{Fe}}(\mathrm{Cn}) _{6}\right]^{4-},\left[\stackrel{\text{III}}{\mathrm{Co}}\left(\mathrm{NH _3}\right) _{6}\right]^{3+},\left[\mathrm{Ti} \left(\mathrm{H _2} \mathrm{O}\right) _{6}\right]^{3+}$ are stable complexes, but no such complexes are known for the second and third transition series such as Mo, W, Rh, In. They form complexes in which their oxidation states are high. For example: $\mathrm{WCl _6}, \mathrm{ReF _7}, \mathrm{RuO _4}$, etc.
(iii) In each of the three transition series, the first ionisation enthalpy increases from left to right. However, there are some exceptions. The first ionisation enthalpies of the third transition series are higher than those of the first and second transition series. This occurs due to the poor shielding effect of 4 felectrons in the third transition series.
Certain elements in the second transition series have higher first ionisation enthalpies than elements corresponding to the same vertical column in the first transition series. There are also elements in the $2^{\text {nd }}$ transition series whose first ionisation enthalpies are lower than those of the elements corresponding to the same vertical column in the $1^{\text {st }}$ transition series.
(iv) Atomic size generally decreases from left to right across a period. Now, among the three transition series, atomic sizes of the elements in the second transition series are greater than those of the elements corresponding to the same vertical column in the first transition series. However, the atomic sizes of the elements in the third transition series are virtually the same as those of the corresponding members in the second transition series. This is due to lanthanoid contraction.
8.36 Write down the number of 3d electrons in each of the following ions:
$\mathrm{Ti}^{2+}, \mathrm{V}^{2+}, \mathrm{Cr}^{3+}, \mathrm{Mn}^{2+}, \mathrm{Fe}^{2+}, \mathrm{Fe}^{3+}, \mathrm{CO}^{2+}, \mathrm{Ni}^{2+}$ and $\mathrm{Cu}^{2+}$.
Indicate how would you expect the five 3d orbitals to be occupied for these hydrated ions (octahedral).
Show Answer
Answer
$ \begin{array}{|c|c|c|} \hline \text{Metal ion} & \text{Number of } \mathbf{d}\text{-electrons} & \text{Filling of } \mathbf{d}\text{-orbitals} \\ \hline \mathrm{Ti}^{2+} & 2 & t_{2 g}^{2} \\ \hline \mathrm{V}^{2+} & 3 & t_{2 g}^{3} \\ \hline \mathrm{Cr}^{3+} & 3 & t_{2 g}^{3} \\ \hline \mathrm{Mn}^{2+} & 5 & t_{2 g}^{3} e_{g}^{2} \\ \hline \mathrm{Fe}^{2+} & 6 & t_{2 g}^{4} e_{g}^{2} \\ \hline \mathrm{Fe}^{3+} & 5 & t_{2 g}^{3} e_{g}^{2} \\ \hline \mathrm{CO}^{2+} & 7 & t_{2 g}^{5} e_{g}^{2} \\ \hline \mathrm{Ni}^{2+} & 8 & t_{2 g}^{6} e_{g}^{2} \\ \hline \mathrm{Cu}^{2+} & 9 & t_{2 g}^{6} e_{g}^{3} \\ \hline \end{array} $
8.37 Comment on the statement that elements of the first transition series possess many properties different from those of heavier transition elements.
Show Answer
Answer
The properties of the elements of the first transition series differ from those of the heavier transition elements in many ways.
(i) The atomic sizes of the elements of the first transition series are smaller than those of the heavier elements (elements of $2^{\text {nd }}$ and $3^{\text {rd }}$ transition series).
However, the atomic sizes of the elements in the third transition series are virtually the same as those of the corresponding members in the second transition series. This is due to lanthanoid contraction.
(ii) +2 and +3 oxidation states are more common for elements in the first transition series, while higher oxidation states are more common for the heavier elements.
(iii) The enthalpies of atomisation of the elements in the first transition series are lower than those of the corresponding elements in the second and third transition series.
(iv) The melting and boiling points of the first transition series are lower than those of the heavier transition elements. This is because of the occurrence of stronger metallic bonding ( $M-M$ bonding).
(v) The elements of the first transition series form low-spin or high-spin complexes depending upon the strength of the ligand field. However, the heavier transition elements form only low-spin complexes, irrespective of the strength of the ligand field.
8.38 What can be inferred from the magnetic moment values of the following complex species?
| Example | Moment Magnetic $(\mathrm{BM})$ |
|---|---|
| $\mathrm{K}_4\left[\mathrm{Mn}(\mathrm{CN})_6\right)$ | 2.2 |
| $\left[\mathrm{Fe}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right]^{2+}$ | 5.3 |
| $\mathrm{~K}_2\left[\mathrm{MnCl}_4\right]$ | 5.9 |
Show Answer
Answer
Magnetic moment $\left(\mu\right)$ is given as $\mu=\sqrt{n(n+2)}$.
For value $n=1, \mu=\sqrt{1(1+2)}=\sqrt{3}=1.732$.
For value $n=2, \quad \mu=\sqrt{2(2+2)}=\sqrt{8}=2.83$.
For value $n=3, \mu=\sqrt{3(3+2)}=\sqrt{15}=3.87$.
For value $n=4, \mu=\sqrt{4(4+2)}=\sqrt{24}=4.899$.
For value $n=5, \mu=\sqrt{5(5+2)}=\sqrt{35}=5.92$.
(i) $\mathrm{K_4}\left[\mathrm{Mn}(\mathrm{CN})_{6}\right]$
For in transition metals, the magnetic moment is calculated from the spin-only formula. Therefore,
$ \sqrt{n(n+2)}=2.2 $
We can see from the above calculation that the given value is closest to $n=1$. Also, in this complex, $\mathrm{Mn}$ is in the +2 oxidation state. This means that Mn has 5 electrons in the $d$-orbital.
Hence, we can say that $\mathrm{CN}$ - is a strong field ligand that causes the pairing of electrons.
(ii) $\left[\mathrm{Fe}\left(\mathrm{H_2} \mathrm{O}\right)_{6}\right]^{2+}$
$ \sqrt{n(n+2)}=5.3 $
We can see from the above calculation that the given value is closest to $n=4$. Also, in this complex, $\mathrm{Fe}$ is in the +2 oxidation state. This means that $\mathrm{Fe}$ has 6 electrons in the $d$-orbital.
Hence, we can say that $\mathrm{H_2} \mathrm{O}$ is a weak field ligand and does not cause the pairing of electrons.
(iii) $\mathrm{K_2}\left[\mathrm{MnCl_4}\right]$
$ \sqrt{n(n+2)}=5.9 $
We can see from the above calculation that the given value is closest to $n=5$. Also, in this complex, $\mathrm{Mn}$ is in the +2 oxidation state. This means that Mn has 5 electrons in the $d$-orbital.
Hence, we can say that $\mathrm{Cl}$ is a weak field ligand and does not cause the pairing of electrons.










