Thinking Process

If the number is less than 1, the zero(s) on the right of decimal point and before the first non-zero digit are not significant.

Answer (b) In $\underline{0}$. $\underline{6} 6900$, the underlined zeroes are not significant. Hence, number of significant figures are four (6900).

• Option (a) is incorrect because it suggests there are 5 significant figures, but the leading zero is not significant, leaving only 4 significant figures (6900).
• Option (c) is incorrect because it suggests there are only 2 significant figures, but the trailing zeroes after the decimal point are significant, making it 4 significant figures (6900).
• Option (d) is incorrect because it suggests there are 3 significant figures, but the trailing zeroes after the decimal point are significant, making it 4 significant figures (6900).

Answer (b) The sum of the numbers can be calculated as 663.821 arithmetically. The number with least decimal places is 227.2 is correct to only one decimal place.

The final result should, therefore be rounded off to one decimal place i.e., 664 .

Note In calculating the sum, we should not confuse with the number of decimal places and significant figures. The result should have least number of decimal places.

• Option (a) 663.821: This option is incorrect because it does not follow the rule of rounding to the least number of decimal places. The number 227.2 has only one decimal place, so the final result should also be rounded to one decimal place, not three.

• Option (c) 663.8: This option is incorrect because it rounds the sum to one decimal place, but it does not account for the proper rounding rules. The correct rounding of 663.821 to one decimal place should be 664, not 663.8.

• Option (d) 663.82: This option is incorrect because it rounds the sum to two decimal places. The number 227.2 has only one decimal place, so the final result should be rounded to one decimal place, not two.

Thinking Process

In multiplication or division, the final result should retain as many significant figures as are there in the original number with the least significant figures.

Answer (c) In this question, density should be reported to two significant figures.

$ \text { Density }=\frac{4.237 g}{2.5 cm^{3}}=1.6948 $

As rounding off the number, we get density $=1.7$

• Option (a) $1.6048 g cm^{-3}$ is incorrect because it does not match the calculated density value of $1.6948 g cm^{-3}$ and also has too many significant figures.
• Option (b) $1.69 g cm^{-3}$ is incorrect because it has three significant figures, whereas the correct answer should be rounded to two significant figures.
• Option (d) $1.695 g cm^{-3}$ is incorrect because it has four significant figures, whereas the correct answer should be rounded to two significant figures.

Answer (d) Rounding off 2.745 to 3 significant figures it would be 2.74 . Rounding off 2.735 to 3 significant figures it would be 2.74 .

• Option (a) 2.75 and 2.74: This option is incorrect because rounding off 2.745 to 3 significant figures should result in 2.74, not 2.75. The digit after the third significant figure is 5, and according to rounding rules, if the digit is exactly 5, you round to the nearest even number, which in this case is 4.

• Option (b) 2.74 and 2.73: This option is incorrect because rounding off 2.735 to 3 significant figures should result in 2.74, not 2.73. The digit after the third significant figure is 5, and according to rounding rules, if the digit is exactly 5, you round to the nearest even number, which in this case is 4.

• Option (c) 2.75 and 2.73: This option is incorrect for two reasons. First, rounding off 2.745 to 3 significant figures should result in 2.74, not 2.75. Second, rounding off 2.735 to 3 significant figures should result in 2.74, not 2.73. The digit after the third significant figure in both cases is 5, and according to rounding rules, if the digit is exactly 5, you round to the nearest even number, which in both cases is 4.

Thinking Process

If $\Delta x$ is error in a physical quantity, then relative error is calculated as $\frac{\Delta x}{x}$.

Answer (a) Given,

$ \begin{aligned} \text { length } l & =(16.2 \pm 0.1) cm \\ \text { Breadth } b & =(10.1 \pm 0.1) cm \\ \text { Area } A & =l \times b \\ & =(16.2 cm) \times(10.1 cm)=163.62 cm^{2} \end{aligned} $

Rounding off to three significant digits, area $A=164 cm^{2}$

$ \begin{aligned} \frac{\Delta A}{A} & =\frac{\Delta l}{l}+\frac{\Delta b}{b}=\frac{0.1}{16.2}+\frac{0.1}{10.1} \\ & =\frac{1.01+1.62}{16.2 \times 10.1}=\frac{2.63}{163.62} \\ \Rightarrow \quad \Delta A & =A \times \frac{2.63}{163.62}=163.62 \times \frac{2.63}{163.62}=2.63 cm^{2} \\ \Delta A & =3 cm^{2} \quad \text { (By rounding off to one significant figure) } \\ \therefore \quad \text { Area, } A & =A \pm \Delta A=(164 \pm 3) cm^{2} . \end{aligned} $

• Option (b): The area is calculated correctly as (163.62 , \text{cm}^2), but the error calculation is incorrect. The error should be rounded to one significant figure, which is (3 , \text{cm}^2), not (2.6 , \text{cm}^2).

• Option (c): The area is rounded to (163.6 , \text{cm}^2), which is incorrect because the area should be rounded to three significant digits, resulting in (164 , \text{cm}^2). Additionally, the error should be rounded to one significant figure, which is (3 , \text{cm}^2), not (2.6 , \text{cm}^2).

• Option (d): The area is calculated correctly as (163.62 , \text{cm}^2), but the error calculation is incorrect. The error should be rounded to one significant figure, which is (3 , \text{cm}^2), not (3 , \text{cm}^2) (as it is already correct). However, the area should be rounded to three significant digits, resulting in (164 , \text{cm}^2).

Answer (c) (a) Work $=$ force $\times$ distance $=[MLT^{-2}][L][ML^{2} T^{-2}]$ Torque $=$ force $\times$ distance $=[ML^{2} T^{-2}]$

(b) Angular momentum $=mvr=[M][LT^{-1}][L]=[ML^{2} T^{-1}]$ Planck’s constant $=\frac{E}{V}=\frac{[ML^{2} T^{-2}]}{[T^{-1}]}=[ML^{2} T^{-1}]$

(c) Tension $=$ force $=[MLT^{-2}]$

Surface tension $=\frac{\text { force }}{\text { length }}=\frac{[MLT^{-2}]}{[L]}=[ML^{0} T^{-2}]$

(d) Impulse $=$ force $\times$ time $=[MLT^{-2}][T]=[MLT^{-1}]$

Momentum $=$ mass $\times$ velocity $=[M][LT^{-1}]=[MLT^{-1}]$

Note One should not be confused with the similar form tension in both the physical quantities-surface tension and tension. Dimensional formula for both of them is not same.

• (a) Work and torque: Both work and torque have the same dimensional formula, which is ([ML^2 T^{-2}]). Therefore, this option is incorrect.

• (b) Angular momentum and Planck’s constant: Both angular momentum and Planck’s constant have the same dimensional formula, which is ([ML^2 T^{-1}]). Therefore, this option is incorrect.

• (d) Impulse and linear momentum: Both impulse and linear momentum have the same dimensional formula, which is ([MLT^{-1}]). Therefore, this option is incorrect.

Answer (a) Given,

$ \begin{aligned} A & =2.5 ms^{-1} \pm 0.5 ms^{-1}, B=0.10 s \pm 0.01 s \\ x & =A B=(2.5)(0.10)=0.25 m \\ \frac{\Delta x}{x} & =\frac{\Delta A}{A}+\frac{\Delta B}{B} \\ & =\frac{0.5}{2.5}+\frac{0.01}{0.10}=\frac{0.05+0.025}{0.25}=\frac{0.075}{0.25} \end{aligned} $

$\Delta x=0.075=0.08 m$, rounding off to two significant figures.

$A B=(0.25 \pm 0.08) m$

• Option (b) $(0.25 \pm 0.5) m$ is incorrect because the calculated uncertainty $\Delta x$ is $0.08 m$, not $0.5 m$. The value $0.5 m$ is significantly larger than the actual uncertainty.

• Option (c) $(0.25 \pm 0.05) m$ is incorrect because the calculated uncertainty $\Delta x$ is $0.08 m$, not $0.05 m$. The value $0.05 m$ is smaller than the actual uncertainty.

• Option (d) $(0.25 \pm 0.135) m$ is incorrect because the calculated uncertainty $\Delta x$ is $0.08 m$, not $0.135 m$. The value $0.135 m$ is larger than the actual uncertainty.

Answer (d) Given,

$ \begin{aligned} & A=1.0 m \pm 0.2 m, B=2.0 m \pm 0.2 m \\ & Y=\sqrt{A B}=\sqrt{(1.0)(2.0)}=1.414 m \end{aligned} $

Let,

Rounding off to two significant digit $Y=1.4 m$

$\frac{\Delta Y}{Y}=\frac{1}{2}[\frac{\Delta A}{A}+\frac{\Delta B}{B}]=\frac{1}{2}[\frac{0.2}{1.0}+\frac{0.2}{2.0}]=\frac{0.6}{2 \times 2.0}$

$\Rightarrow \Delta Y=\frac{0.6 Y}{2 \times 2.0}=\frac{0.6 \times 1.4}{2 \times 2.0}=0.212$

Rounding off to one significant digit $\Delta Y=0.2 m$

Thus, correct value for $\sqrt{A B}=r+\Delta r=1.4 \pm 0.2 m$

• Option (a) $1.4 m \pm 0.4 m$ is incorrect because the uncertainty $\pm 0.4 m$ is too large. The correct calculation of the uncertainty yields $\pm 0.2 m$.

• Option (b) $1.41 m \pm 0.15 m$ is incorrect because the value $1.41 m$ is not rounded to two significant digits as required. Additionally, the uncertainty $\pm 0.15 m$ is not consistent with the correct calculation, which yields $\pm 0.2 m$.

• Option (c) $1.4 m \pm 0.3 m$ is incorrect because the uncertainty $\pm 0.3 m$ is too large. The correct calculation of the uncertainty yields $\pm 0.2 m$.

Answer (a) All given measurements are correct upto two decimal places. As here $5.00 mm$ has the smallest unit and the error in $5.00 mm$ is least (commonly taken as $0.01 mm$ if not specified), hence, $5.00 mm$ is most precise.

Note In solving these type of questions, we should be careful about units although their magnitude is same.

• $5.00 cm$: Although it is correct up to two decimal places, the unit is larger than $5.00 mm$, resulting in a larger absolute error (commonly taken as $0.01 cm$ if not specified), making it less precise than $5.00 mm$.

• $5.00 m$: This measurement is also correct up to two decimal places, but the unit is even larger than $5.00 cm$, resulting in an even larger absolute error (commonly taken as $0.01 m$ if not specified), making it less precise than both $5.00 mm$ and $5.00 cm$.

• $5.00 km$: While it is correct up to two decimal places, the unit is the largest among the options, resulting in the largest absolute error (commonly taken as $0.01 km$ if not specified), making it the least precise compared to $5.00 mm$, $5.00 cm$, and $5.00 m$.

Answer (a) Given length

$ l=5 cm $

Now, checking the errors with each options one by one, we get

Error $\Delta l_1$ is least.

$ \begin{aligned} & \Delta l_1=5-4.9=0.1 cm \\ & \Delta l_2=5-4.805=0.195 cm \\ & \Delta l_3=5.25-5=0.25 cm \\ & \Delta l_4=5.4-5=0.4 cm \end{aligned} $

Hence, $4.9 cm$ is most precise.

• Option (b) $4.805 cm$ is incorrect because the error $\Delta l_2 = 0.195 cm$ is larger than the error for $4.9 cm$.
• Option (c) $5.25 cm$ is incorrect because the error $\Delta l_3 = 0.25 cm$ is larger than the error for $4.9 cm$.
• Option (d) $5.4 cm$ is incorrect because the error $\Delta l_4 = 0.4 cm$ is larger than the error for $4.9 cm$.

Answer (c) Given, Young’s modulus

$ \begin{aligned} Y & =1.9 \times 10^{11} N / m^{2} \\ 1 N & =10^{5} \text { dyne } \\ Y & =1.9 \times 10^{11} \times 10^{5} \text { dyne } / m^{2} \\ 1 m & =100 cm \\ Y & =1.9 \times 10^{11} \times 10^{5} \text { dyne } /(100)^{2} cm^{2} \\ & =1.9 \times 10^{16-4} \text { dyne } / cm^{2} \\ Y & =1.9 \times 10^{12} \text { dyne } / cm^{2} \end{aligned} $

Hence,

We know that

Note While we are going through units conversion, we should keep in mind that proper relation between units are mentioned.

• Option (a) $1.9 \times 10^{10}$: This option is incorrect because it underestimates the conversion factor. The correct conversion involves multiplying by $10^{16-4}$, which results in $1.9 \times 10^{12}$, not $1.9 \times 10^{10}$.

• Option (b) $1.9 \times 10^{11}$: This option is incorrect because it does not account for the full conversion from $N/m^2$ to dyne/cm^2. The correct conversion factor is $10^{16-4}$, leading to $1.9 \times 10^{12}$, not $1.9 \times 10^{11}$.

• Option (d) $1.9 \times 10^{13}$: This option is incorrect because it overestimates the conversion factor. The correct conversion results in $1.9 \times 10^{12}$ dyne/cm^2, not $1.9 \times 10^{13}$.

Answer (d) Given, fundamental quantities are momentum $(p)$, area $(A)$ and time $(T)$. We can write energy $E$ as

$ \begin{aligned} & E \propto p^{a} A^{b} T^{c} \\ & E=k p^{a} A^{A} T^{c} \end{aligned} $

where $k$ is dimensionless constant of proportionality.

Dimensions of

$ \begin{aligned} E & =[E]=[ML^{2} T^{-2}] \text { and }[p]=[MLT^{-1}] \\ {[A] } & =[L^{2}] \\ {[T] } & =[T] \\ {[E] } & =[K][p]^{a}[A]^{b}[T]^{c} \end{aligned} $

Putting all the dimensions, we get

$ \begin{aligned} ML^{2} T^{-2} & =[MLT^{-1}]^{a}[L^{2}]^{b}[T]^{c} \\ & =M^{a} L^{2 b+a} T^{-a+c} \end{aligned} $

By principle of homogeneity of dimensions,

$ a =1,2 b+a=2 $

$\Rightarrow 2 b+1 =2 $

$\Rightarrow b =1 / 2-a+c=-2 $

$\Rightarrow c =-2+a=-2+1=-1 $

$\text{ Hence, } E =p A^{1 / 2} T^{-1}$

• Option (a) $[pA^{-1} T^{1}]$: This option is incorrect because the dimensional analysis does not match the dimensions of energy. The dimensions of energy are $[ML^2 T^{-2}]$, but the given option has dimensions $[MLT^{-1}][L^{-2}][T] = [ML^{-1}T^0]$, which does not equate to the dimensions of energy.

• Option (b) $[p^{2} AT]$: This option is incorrect because the dimensional analysis does not match the dimensions of energy. The dimensions of energy are $[ML^2 T^{-2}]$, but the given option has dimensions $[MLT^{-1}]^2[L^2][T] = [M^2L^4T^{-2}][T] = [M^2L^4T^{-1}]$, which does not equate to the dimensions of energy.

• Option (c) $[p A^{-1 / 2} T]$: This option is incorrect because the dimensional analysis does not match the dimensions of energy. The dimensions of energy are $[ML^2 T^{-2}]$, but the given option has dimensions $[MLT^{-1}][L^{-1}][T] = [ML^0T^0] = [M]$, which does not equate to the dimensions of energy.

Thinking Process

We know that angle is dimensionless. Here, $a$ is displacement and $y$ is also displacement, hence they are having same dimensions.

Answer $(b, c)$

Now, by principle of homogeneity of dimensions LHS and RHS of (a) and (d) will be same and is $L$.

For (c)

$ \begin{aligned} & {[LHS]=L} \\ & {[RHS]=\frac{L}{T}=LT^{-1}} \\ & {[LHS] \neq[RHS]} \end{aligned} $

Hence, (c) is not correct option.

In option (b) dimension of angle is [vt ]i.e., $L$

$ \begin{matrix} \Rightarrow & R H S=L . L=L^{2} \text { and } L H S=L \\ \Rightarrow & L H S \neq R H S . \end{matrix} $

So, option (b) is also not correct.

• For option (b):

  • The dimension of the angle in the sine function is [vt], which is $[L]$.
  • Therefore, the RHS has dimensions $L \cdot L = L^2$.
  • The LHS has dimensions $L$.
  • Hence, $[LHS] \neq [RHS]$.

• For option (c):

  • The LHS has dimensions $L$.
  • The RHS has dimensions $\frac{L}{T} = LT^{-1}$.
  • Hence, $[LHS] \neq [RHS]$.

Thinking Process

We should keep in mind that when two physical quantities are added or subtracted they should have same dimensions.

Answer $(a, e)$

In this question, it is given that $P, Q$ and $R$ are having different dimensions, hence they cannot be added or subtracted, so we can say that (a) and (e) are not meaningful. We cannot say about the dimension of product of these quantities, hence (b), (c) and (d) may be meaningful.

Note In this question, we are certain about the quantity which is never meaningful but we should keep in mind that others may or may not be meaningful.

• For option (b) (PQ - R):

  • The product (PQ) results in a new quantity with dimensions that are a combination of the dimensions of (P) and (Q). Since (R) has different dimensions, subtracting (R) from (PQ) is not meaningful because quantities with different dimensions cannot be added or subtracted.

• For option (c) (PQ / R):

  • The product (PQ) divided by (R) results in a new quantity with dimensions that are a combination of the dimensions of (P), (Q), and (R). This combination can result in a meaningful quantity depending on the specific dimensions of (P), (Q), and (R).

• For option (d) ((PR - Q^2) / R):

  • The term (PR) has dimensions that are a combination of (P) and (R), and (Q^2) has dimensions that are the square of (Q). Since (P), (Q), and (R) have different dimensions, (PR) and (Q^2) cannot be subtracted meaningfully. However, the entire expression ((PR - Q^2) / R) can still result in a meaningful quantity depending on the specific dimensions of (P), (Q), and (R).

• For option (e) ((R + Q) / P):

  • The sum (R + Q) is not meaningful because (R) and (Q) have different dimensions and cannot be added. Therefore, the entire expression ((R + Q) / P) is not meaningful.

Answer

( $b, d)$

We know that energy of radiation, $E=h v$

$ [h]=\frac{[E]}{[v]}=\frac{[ML^{2} T^{-2}]}{[T^{-1}]}=[ML^{2} T^{-1}] $

Dimension of linear impulse $=$ Dimension of momentum $=[MLT^{-1}]$

As we know that linear impulse $J=\Delta P$

$\Rightarrow \quad$ Angular impulse $=\tau d t=\Delta L=$ Change in angular momentum

Hence, dimension of angular impulse

$ \begin{aligned} & =\text { Dimension of angular momentum } \\ & =[ML^{2} T^{-1}] . \end{aligned} $

This is similar to the dimension of Planck’s constant $h$.

• Option (a) linear impulse: The dimension of linear impulse is the same as that of linear momentum, which is ([MLT^{-1}]). This is different from the dimension of Planck’s constant (h), which is ([ML^2T^{-1}]).

• Option (c) linear momentum: The dimension of linear momentum is ([MLT^{-1}]). This does not match the dimension of Planck’s constant (h), which is ([ML^2T^{-1}]).

Answer

$(a, b, d)$

We know that dimension of $h=[h]=[ML^{2} T^{-1}]$

$[c]=[LT^{-1}],[m_{e}]=M$

$[G]=[M^{-1} L^{3} T^{-2}]$

$[e]=[A T],[m_{p}]=[M]$

$[\frac{h c}{G}]=\frac{[ML^{2} T^{-1}][LT^{-1}]}{[M^{-1} L^{3} T^{-2}]}=[M^{2}]$

$M=\sqrt{\frac{h c}{G}}$

Similarly,

$\frac{h}{c}=\frac{[ML^{2} T^{-1}]}{[LT^{-1}]}=[ML]$

$L=\frac{h}{c M}=\frac{h}{c} \sqrt{\frac{G}{h c}}=\frac{\sqrt{G h}}{c^{3 / 2}}$

As,

$ c=L T^{-1} $

$\Rightarrow \quad[T]=\frac{[L]}{[c]}=\frac{\sqrt{G h}}{c^{3 / 2} \cdot c}=\frac{\sqrt{G h}}{c^{5 / 2}}$

Hence, (a), (b) or (d) any can be used to express $L, M$ and $T$ in terms of three chosen fundamental quantities.

• Option (c) Charge of electron (e) is incorrect because its dimension is $[A T]$, which involves the unit of electric current (A). Since the chosen fundamental quantities are Planck’s constant $(h)$ and speed of light in vacuum $(c)$, which do not involve electric current, the charge of the electron cannot be used to express length, mass, and time in terms of the three chosen fundamental quantities.

Thinking Process

While solving this type of questions, we should first write an expression and try to express it in terms of quantities given in the option.

Answer $(a, b)$

We know that pressure $=\frac{\text { Force }}{\text { Area }}$

$ \text { Pressure }=\frac{\text { Force } \times \text { Distance }}{\text { Area } \times \text { Distance }}=\frac{\text { Work }}{\text { Volume }}=\frac{\text { Energy }}{\text { Volume }} $

Note Here, we should keep it in mind that above values are not exactly equal but these are equivalent with respect to their units.

• Option (c) Energy/Area: This ratio does not express pressure because pressure is defined as force per unit area, not energy per unit area. Energy per unit area would represent a different physical quantity, such as energy density on a surface.

• Option (d) Force/Volume: This ratio does not express pressure because pressure is defined as force per unit area, not force per unit volume. Force per unit volume would represent a different physical quantity, such as force density.

Answer $(b, d)$

We know that 1 light year $=9.46 \times 10^{11} m$

$=$ distance that light travels in 1 year with speed $3 \times 10^{8} m / s$.

1 parsec $=3.08 \times 10^{16} m$

$=$ Distance at which average radius of earth’s orbit subtends an angle of 1 parsecond

Here, second and year represent time.

• Parsec: A parsec is a unit of distance used in astronomy to measure large distances to objects outside our solar system. It is equivalent to approximately 3.26 light-years or about 3.08 × 10^16 meters. It is not a unit of time.

• Light year: A light year is also a unit of distance, not time. It represents the distance that light travels in one year in a vacuum, which is approximately 9.46 × 10^12 kilometers or about 5.88 × 10^12 miles.

Answer The value of any given physical quantity may vary over a wide range, therefore, different units of same physical quantity are required.

e.g., The length of a pen can be easily measured in $cm$, the height of a tree can be measured in metres, the distance between two cities can be measured in kilometres and distance between two heavenly bodies can be measured in light year.

Answer

$ \begin{aligned} \text { Radius of atom } & =1 \AA=10^{-10} m \\ \text { Radius of nucleus } & =1 \text { fermi }=10^{-15} m \\ \text { Volume of atom } & =V_{A}=\frac{4}{3} \pi R_A^{3} \\ \text { Volume of nucleus } V_{N} & =\frac{4}{3} \pi R_N^{3} \\ \frac{V_{A}}{V_{N}} & =\frac{\frac{4}{3} \pi R_A^{3}}{\frac{4}{3} \pi R_N^{3}}=(\frac{R_{A}}{R_{N}})^{3}=(\frac{10^{-10}}{10^{-15}})^{3}=10^{15} \end{aligned} $

Note In such type of questions, always change the value in same unit.

Answer One atomic mass unit is the $\frac{1}{12}$ of the mass of $a_6 C^{12}$ atom.

Mass of one mole of $ _6 C^{12}$ atom $=12 g$

Number of atoms in one mole $=$ Avogadro’s number

$ =6.023 \times 10^{23} $

$ \begin{aligned} \therefore \quad \text { Mass of one } _6 C^{12} \text { atom } & =\frac{12}{6.023 \times 10^{23}} g \\ 1 amu & =\frac{1}{12} \times \text { mass of one } _6 C^{12} \text { atom } \\ \therefore \quad 1 amu & =(\frac{1}{12} \times \frac{12}{6.023 \times 10^{23}}) g=1.67 \times 10^{-24} g \\ & =1.67 \times 10^{-27} kg \quad(\because 1 g=10^{-3} kg) \end{aligned} $

Answer Length, mass and time are chosen as base quantities in mechanics because

(i) Length, mass and time cannot be derived from one another, that is these quantities are independent.

(ii) All other quantities in mechanics can be expressed in terms of length, mass and time.

Thinking Process

To solve this question, we have to treat radius of earth as an arc as seen from the moon.

Answer (a) Angle subtended at distance $r$ due to an arc of length $l$ is

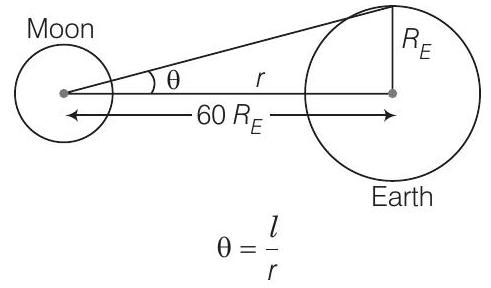
Given,

$ \begin{aligned} l & =R_{E} ; r=60 R_{E} \\ \theta & =\frac{R_{E}}{60 R_{E}}=\frac{1}{60} rad=\frac{1}{60} \times \frac{180}{\pi} \text { degree } \\ & =\frac{3}{\pi} \approx 1^{\circ} \end{aligned} $

Hence, angle subtended by diameter of the earth $=2 \theta=2^{\circ}$.

(b) Given that moon is seen as $(\frac{1}{2})^{\circ}$ diameter and earth is seen as $2^{\circ}$ diameter.

Hence,

$ \frac{\text { Diameter of earth }}{\text { Diameter of moon }}=\frac{(2 / \pi) rad}{(\frac{1}{2 \pi}) rad}=4 $

(c) From parallax measurement given that sun is at a distance of about 400 times the earth-moon distance, hence, $\frac{r_{\text {sun }}}{r_{\text {moon }}}=400$

(Suppose, here $r$ stands for distance and $D$ for diameter) sun and moon both appear to be of the same angular diameter as seen from the earth.

$ \begin{matrix} \therefore & \frac{D_{\text {sun }}}{r_{\text {sun }}}=\frac{D_{\text {moon }}}{r_{\text {moon }}} \\ \therefore & \frac{D_{\text {sun }}}{D_{\text {moon }}}=400 \\ \text { But } & \frac{D_{\text {earth }}}{D_{\text {moon }}}=4 \\ \therefore & \frac{D_{\text {sun }}}{D_{\text {earth }}}=100 \end{matrix} $

Answer Given, distance of the galaxy $=10^{25} m$

$ \text { Speed of light }=3 \times 10^{8} m / s $

Hence, time taken by light to reach us from galaxy is,

$ \begin{aligned} t & =\frac{\text { Distance }}{\text { Speed }}=\frac{10^{25}}{3 \times 10^{8}} \approx \frac{1}{3} \times 10^{17} \\ & =\frac{10}{3} \times 10^{16}=3.33 \times 10^{16} s \end{aligned} $

Thinking Process

Inaccuracy will be measured by difference of MSD and 1VSD, where MSD = main scale division and VSD = verneir scale division.

Answer By question, it is given that

$ \begin{aligned} 50 VSD & =49 MSD \\ 1 MSD & =\frac{50}{49} VSD \\ 1 VSD & =\frac{49}{50} MSD \\ \text { ccuracy } & =1 MSD-1 VSD \\ & =1 MSD-\frac{49}{50} MSD=\frac{1}{50} MSD \end{aligned} $

$ \text { Minimum inaccuracy }=1 MSD-1 VSD $

Given,

Hence,

$ \begin{aligned} 1 MSD & =0.5 mm \\ \text { minimum inaccuracy } & =\frac{1}{50} \times 0.5 mm=\frac{1}{100}=0.01 mm \end{aligned} $

Answer

Consider the diagram given below

$R_{m e}=$ Distance of moon from earth

$R_{\text {se }}=$ Distance of sun from earth

Let angle made by sun and moon is $\theta$, we can write

$ \theta=\frac{A_{\text {sun }}}{R_se^{2}}=\frac{A_{\text {moon }}}{R_{\text {me }}^{2}} $

Here,

$A_{\text {sun }}=$ Area of the sun

$A_{\text {moon }}=$ Area of the moon

$ \begin{matrix} \Rightarrow & & \theta & =\frac{\pi R_s^{2}}{R_{s e}^{2}}=\frac{\pi R_m^{2}}{R_{m e}^{2}} \\ \Rightarrow & & (\frac{R_{s}}{R_{s e}})^{2} & =(\frac{R_{m}}{R_{m e}})^{2} \\ \Rightarrow & \frac{R_{s}}{R_{s e}} & =\frac{R_{m}}{R_{m e}} \\ \Rightarrow & \frac{R_{s}}{R_{m}} & =\frac{R_{s e}}{R_{m e}} \end{matrix} $

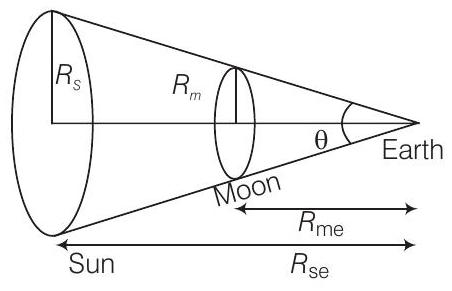
(Here, radius of sun and moon represents their sizes respectively)

Thinking Process

First write dimension of each quantity and then relate them.

Answer Dimension of force $F=[MLT^{-2}]=100 N$

$\begin{aligned} \text { Length }(L) & =[L]=10 m \\ Time(t) & =[T]=100 s\end{aligned}$

Substituting values of $L$ and $T$ from Eqs. (ii) and (iii) in Eq. (i), we get

$ M \times 10 \times(100)^{-2}=100 $

$\Rightarrow \quad \frac{M \times 10}{100 \times 100}=100$

$\Rightarrow \quad M=100 \times 1000 kg$

$M=10^{5} kg$

Answer (a) Plane angle $\theta=\frac{L}{r}$ radian

its unit is radian but has no dimensions

(b) Strain $=\frac{\Delta L}{L}=\frac{\text { Change in length }}{\text { length }}$

It has neither unit nor dimensions

(c) Gravitational constant $(G)=6.67 \times 10^{-11} N-m^{2} / kg^{2}$

(d) Reynold’s number is a constant which has no unit.

Answer We know that angle

$ \begin{aligned} & \theta=\frac{l}{r} \text { radian } \\ & \theta=\frac{\pi}{6}=\frac{l}{31} cm \end{aligned} $

Given,

Hence,

$ \text { length }=l=31 \times \frac{\pi}{6} cm=\frac{31 \times 3.14}{6} cm=16.22 cm $

Rounding off to three significant figures it would be $16.2 cm$.

Answer We know that solid angle $\Omega=\frac{\text { Area }}{(\text { Distance }^{2}.}$

$ =\frac{1 cm^{2}}{(5 cm)^{2}}=\frac{1}{25}=4 \times 10^{-2} \text { steradian } $

$(\because.$ Area $=1 cm^{2}$, distance $.=5 cm)$

Note We should not confuse, solid angle with plane angle $\theta=\frac{l}{r}$ radian.

Thinking Process

In solving these type of questions, we should apply principle of homogeneity of dimensions.

Answer Now, by the principle of homogeneity, i.e., dimensions of LHS and RHS should be equal, hence

$[LHS]=[RHS]$

$\Rightarrow$

$[L]=[A]=L$

As $\omega t-k x$ should be dimensionless, $[\omega t]=[k x]=1$

$\begin{matrix} \Rightarrow & {[\omega] T=[k] L=1}\end{matrix} $

$\Rightarrow \quad[\omega]=T^{-1}$ and $[k]=L^{-1}$

Thinking Process

We will apply formula for mean value, absolute error as well as mean absolute error.

Answer Given, $\quad t_1=39.6 s, t_2=39.9 s$ and $t_3=39.5 s$

Least count of measuring instrument $=0.1 s$

(As measurements have only one decimal place)

Precision in the measurement $=$ Least count of the measuring instrument $=0.1 s$

Mean value of time for 20 oscillations is given by

$ \begin{aligned} t & =\frac{t_1+t_2+t_3}{3} \\ & =\frac{39.6+39.9+39.5}{3}=39.7 s \end{aligned} $

Absolute errors in the measurements

$ \begin{aligned} & \Delta t_1=t-t_1=39.7-39.6=0.1 s \\ & \Delta t_2=t-t_2=39.7-39.9=-0.2 s \\ & \Delta t_3=t-t_3=39.7-39.5=0.2 s \\ & \text { Mean absolute error }= \frac{|\Delta t_1|+|\Delta t_2|+|\Delta t_3|}{3} \\ &= \frac{0.1+0.2^{2}+0.2}{3} \\ &= \frac{0.5}{3}=0.17 \approx 0.2 \quad \text { (rounding off upto one decimal place) } \end{aligned} $

$\therefore \quad$ Accuracy of measurement $= \pm 0.2 s$

Thinking Process

For solving this question, we will apply the formula for a system of unit $u, n u=$ constant.

Answer We know that dimension of energy $=[ML^{2} T^{-2}]$

Let $M_1, L_1, T_1$ and $M_2, L_2, T_2$ are units of mass, length and time in given two systems.

$ \begin{matrix} \therefore \quad & M_1=1 kg, L_1=1 m, T_1=1 s \\ M_2 & =\alpha kg, L_2=\beta m, T_2=\gamma s \end{matrix} $

The magnitude of a physical quantity remains the same, whatever be the system of units of its measurement i.e. $n_1 u_1=n_2 u_2$

$ \begin{aligned} \Rightarrow \quad n_2 & =n_1 \frac{u_1}{u_2}=n_1 \frac{[M_1 L_1^{2} T_1^{-2}]}{[M_2 L_2^{2} T_2^{-2}]}=5[\frac{M_1}{M_2}] \times[\frac{L_1}{L_2}]^{2} \times[\frac{T_1}{T_2}]^{-2} \\ & =5[\frac{1}{\alpha} kg] \times[\frac{1}{\beta} m]^{2} \times[\frac{1}{\gamma} s]^{-2} \\ & =5 \times \frac{1}{\alpha} \times \frac{1}{\beta^{2}} \times \frac{1}{\gamma^{-2}} \\ n_2 & =\frac{5 \gamma^{2}}{\alpha \beta^{2}} \end{aligned} $

Thus, new unit of energy will be $\frac{\gamma^{2}}{\alpha \beta^{2}}$.

Thinking Process

If dimensions of LHS of an equation is equal to dimensions of RHS, then equation is said to be dimensionally correct.

Answer The volume of a liquid flowing out per second of a pipe is given by $V=\frac{\pi}{8} \frac{p r^{4}}{\eta l}$

Dimension of V= $\frac{\text { Dimension of volume }}{\text { Dimension of time }}=\frac{[L^{3}]}{[T]}=[L^{3} T^{-1}]$

$(\because V$ is the volume of liquid flowing out per second)

Dimension of p =$[ML^{-1} T^{-2}] $

Dimension of $\eta =[ML^{-1} T^{-1}] $

Dimension of l =[L]

Dimension of r =[L]

Dimensions of LHS, $[V]=\frac{[L^{3}]}{[T]}=[L^{3} T^{-1}]$

Dimensions of RHS, $\frac{[ML^{-1} T^{-2}] \times[L^{4}]}{[ML^{-1} T^{-1}] \times[L]}=[L^{3} T^{-1}]$

As dimensions of LHS is equal to the dimensions of RHS.

Therefore, equation is correct dimensionally.

Thinking Process

We will apply the formula for percentage error in quantity $x$, as $\frac{\Delta x}{x} \times 100$.

Answer Given, physical quantity is $X=a^{2} b^{3} c^{5 / 2} d^{-2}$

Maximum percentage error in $X$ is

$ \begin{aligned} \frac{\Delta X}{X} \times 100 & = \pm[2(\frac{\Delta a}{a} \times 100)+3(\frac{\Delta b}{b} \times 100)+\frac{5}{2}(\frac{\Delta c}{c} \times 100)+2(\frac{\Delta d}{d} \times 100)] \\ & = \pm[2(1)+3(2)+\frac{5}{2}(3)+2(4)] % \\ & = \pm[2+6+\frac{15}{2}+8]= \pm 23.5 % \end{aligned} $

$\therefore$ Percentage error in quantity $X= \pm 23.5 %$

Mean absolute error in $X= \pm 0.235= \pm 0.24 \quad$ (rounding-off upto two significant digits)

The calculated value of $x$ should be round-off upto two significant digits.

$\therefore \quad X=2.8$

Thinking Process

A dimensionless quantity will have dimensional formula as $[M^{0} L^{0} T^{0}]$.

Answer Given, expression is

$ \begin{aligned} P & =E L^{2} m^{-5} G^{-2} \\ {[E] } & =[M L^{2} T^{-2}] \\ {[m] } & =[M] \\ {[L] } & =[M L^{2} T^{-1}] \\ {[G] } & =[M^{-1} L^{3} T^{-2}] \end{aligned} $

where $E$ is energy

$m$ is mass

$L$ is angular momentum

$G$ is gravitational constant

Substituting dimensions of each term in the given expression,

$ \begin{aligned} {[P] } & =[ML^{2} T^{-2}] \times[ML^{2} T^{-1}]^{2} \times[M]^{-5} \times[M^{-1} L^{3} T^{-2}]^{-2} \\ & =[M^{1+2-5+2} L^{2+4-6} T^{-2-2+4}]=[M^{0} L^{0} T^{0}] \end{aligned} $

Therefore, $P$ is a dimensionless quantity.

Thinking Process

In this problem, we have to apply principle of homogeneity of dimensions that is LHS and RHS of an equation will have same dimensions.

Answer We know that, dimensions of

$ (h)=[ML^{2} T^{-1}] $

Dimensions of

$(c)=[L T^{-1}]$

Dimensions of gravitational constant

$ (G)=[M^{-1} L^{3} T^{-2}] $

(i) Let

$m \propto c^{x} h^{y} G^{z}$

$\Rightarrow \quad m=k c^{x} h^{y} G^{z}$

where, $k$ is a dimensionless constant of proportionality.

Substituting dimensions of each term in Eq. (i), we get

$ \begin{aligned} {[ML^{0} T^{0}] } & =[LT^{-1}]^{x} \times[ML^{2} T^{-1}]^{y}[M^{-1} L^{3} T^{-2}]^{z} \\ & =[M^{y-z} L^{x+2 y+3 z} T^{-x-y-2 z}] \end{aligned} $

Comparing powers of same terms on both sides, we get

$ \begin{matrix} y-z=1 \\ x+2 y+3 z=0 \\ -x-y-2 z=0 \end{matrix} $

Adding Eqs. (ii), (iii) and (iv), we get

$ 2 y=1 \Rightarrow y=\frac{1}{2} $

Substituting value of $y$ in Eq. (ii), we get

$ z=-\frac{1}{2} $

From Eq. (iv)

$ x=-y-2 z $

Substituting values of $y$ and $z$, we get

$ x=-\frac{1}{2}-2(-\frac{1}{2})=\frac{1}{2} $

Putting values of $x, y$ and $z$ in Eq. (i), we get

$ m=k c^{1 / 2} h^{1 / 2} G^{-1 / 2} $

$ \Rightarrow \quad m=k \sqrt{\frac{c h}{G}} $

(ii) Let

$ L \propto c^{x} h^{y} G^{z} $

$ \Rightarrow \quad L=k c^{x} h^{y} G^{z} $

where, $k$ is a dimensionless constant.

Substituting dimensions of each term in Eq. (v), we get

$ \begin{aligned} {[M^{0} LT^{0}] } & =[LT^{-1}]^{x} \times[ML^{2} T^{-1}]^{y} \times[M^{-1} L^{3} T^{-2}]^{z} \\ & =[M^{y-z} L^{x+2 y+3 z} T^{-x-y-2 z}] \end{aligned} $

On comparing powers of same terms, we get

$ \begin{matrix} y-z=0 \\ x+2 y+3 z=1 \\ -x-y-2 z=0 \end{matrix} $

Adding Eqs. (vi), (vii) and (viii), we get

$\begin{matrix} & & 2 y=1 \\ y & y & =\frac{1}{2}\end{matrix} $

Substituting value of $y$ in Eq. (vi), we get

$ z=\frac{1}{2} $

From Eq. (viii),

$ x=-y-2 z $

Substituting values of $y$ and $z$, we get

$ x=-\frac{1}{2}-2(\frac{1}{2})=-\frac{3}{2} $

Putting values of $x, y$ and $z$ in Eq. (v), we get

$ \begin{aligned} & L=k c^{-3 / 2} h^{1 / 2} G^{1 / 2} \\ & L=k \sqrt{\frac{h G}{c^{3}}} \end{aligned} $

(iii) Let $T \propto c^{x} h^{y} G^{z}$

$ \Rightarrow \quad T=k c^{x} h^{y} G^{z} $

where, $k$ is a dimensionless constant.

Substituting dimensions of each term in Eq. (ix), we get

$ \begin{aligned} {[M^{0} L^{0} T.} & =[LT^{-1}]^{x} \times[ML^{2} T^{-1}]^{y} \times[M^{-1} L^{3} T^{-2}]^{z} \\ & =[M^{y-z} L^{x+2 y+3 z} T^{-x-y-2 z}] \end{aligned} $

On comparing powers of same terms, we get

$ \begin{matrix} y-z=0 \\ x+2 y+3 z=0 \\ -x-y-2 z=1 \end{matrix} $

Adding Eqs. (x), (xi) and (xii), we get

$ \begin{aligned} & 2 y & =1 \\ \Rightarrow & y & =\frac{1}{2} \end{aligned} $

Substituting value of $y$ in Eq. ( $x$ ), we get

$ z=y=\frac{1}{2} $

From Eq. (xii),

$ x=-y-2 z-1 $

Substituting values of $y$ and $z$, we get

$ x=-\frac{1}{2}-2(\frac{1}{2})-1=-\frac{5}{2} $

Putting values of $x, y$ and $z$ in Eq. (ix), we get

$ \begin{aligned} T & =k c^{-5 / 2} h^{1 / 2} G^{1 / 2} \\ T & =k \sqrt{\frac{h G}{c^{5}}} \end{aligned} $

Thinking Process

In this problem, we have to apply Kepler’s third law, $T^{2} \propto a^{3}$ i.e., square of time period $(T^{2})$ of a satellite revolving around a planet, is proportional to cube of the radius of the orbit $(a^{3})$.

Answer By Kepler’s third law, $\quad T^{2} \propto r^{3} \Rightarrow T \propto r^{3 / 2}$

We know that $T$ is a function of $R$ and $g$.

Let

$ \begin{aligned} & T \propto r^{3 / 2} R^{a} g^{b} \\ & T=k r^{3 / 2} R^{a} g^{b} \end{aligned} $

where, $k$ is a dimensionless constant of proportionality.

Substituting the dimensions of each term in Eq. (i), we get

$ \begin{aligned} {[M^{0} L^{0} T] } & =k[L]^{3 / 2}[L]^{a}[LT^{-2}]^{b} \\ & =k[L^{a+b+3 / 2} T^{-2 b}] \end{aligned} $

On comparing the powers of same terms, we get

$ \begin{aligned} a+b+3 / 2 & =0 \\ -2 b & =1 \Rightarrow b=-1 / 2 \end{aligned} $

From Eq. (ii), we get

$ a-1 / 2+3 / 2=0 \Rightarrow a=-1 $

Substituting the values of $a$ and $b$ in Eq. (i), we get

$ \begin{matrix} \Rightarrow & T & =k r^{3 / 2} R^{-1} g^{-1 / 2} \\ T & =\frac{k}{R} \sqrt{\frac{r^{3}}{g}} \end{matrix} $

Note When we are applying formulae, we should be careful about $r$ (radius of orbit) and $R$ (radius of planet).

Answer (a) Oleic acid does not dissolve in water hence, it is dissolved in alcohol.

(b) Lycopodium powder spreads over the entire surface of water when it is sprinkled evenly. When a drop of prepared solution is dropped on water, oleic acid does not dissolve in water. Instead it spreads on the water surface pushing the lycopodium powder away to clear a circular area where the drop falls. We can therefore, measure the area over which oleic acid spreads.

(c) In each $mL$ of solution prepared volume of oleic acid $=\frac{1}{20} mL \times \frac{1}{20}=\frac{1}{400} mL$

(d) Volume of $n$ drops of this solution of oleic acid can be calculated by means of a burette and measuring cylinder and measuring the number of drops.

(e) If $n$ drops of the solution make $1 mL$, the volume of oleic acid in one drop will be $\frac{1}{(400) n} mL$.

Answer (a) By definition,

1 parsec $=$ Distance at which $1 AU$ long arc subtends an angle of $1 s$.

$ \begin{aligned} \therefore & 1 \text { parsec } & =(\frac{1 AU}{1 arcsec}) \\ \therefore & 1 deg & =3600 arcsec \\ \therefore & 1 \text { parsec } & =\frac{\pi}{3600 \times 180} rad \\ & 1 \text { parsec } & =\frac{3600 \times 180}{\pi} AU=206265 AU \approx 2 \times 10^{5} AU \end{aligned} $

(b) Sun’s diameter is $(\frac{1}{2})^{\circ}$ at $1 AU$.

Therefore, at 1 parsec, star is $\frac{1 / 2}{2 \times 10^{5}}$ degree in diameter $=15 \times 10^{-5}$ arc min.

With 100 magnification, it should look $15 \times 10^{-3}$ arcmin. However, due to atmospheric fluctuations, it will still look of about 1 arcmin. It cannot be magnified using telescope.

(c) Given that

$ \frac{D_{\text {mars }}}{D_{\text {earth }}}=\frac{1}{2} $

where $D$ represents diameter.

From answer 25(e)

$\begin{matrix} \text { we know that, } & \frac{D_{\text {earth }}}{D_{\text {sun }}}=\frac{1}{100} \\ \therefore & \frac{D_{\text {mars }}}{D_{\text {sun }}}=\frac{1}{2} \times \frac{1}{100}\end{matrix} $

[from Eq. (i)]

$ \begin{aligned} & \text { At } 1 AU \text { sun’s diameter }=(\frac{1}{2})^{\circ} \\ & \therefore \quad \text { mar’s diameter }=\frac{1}{2} \times \frac{1}{200}=\frac{1}{400} \\ & \text { At } \frac{1}{2} AU, \text { mar’s diameter }=\frac{1}{400} \times 2^{\circ}=(\frac{1}{200})^{\circ} \end{aligned} $

With 100 magnification, Mar’s diameter $=\frac{1}{200} \times 100^{\circ}=(\frac{1}{2})^{\circ}=30^{\prime}$

This is larger than resolution limit due to atmospheric fluctuations. Hence, it looks magnified.

Thinking Process

In this problem, we have to apply Einstein’s mass-energy relation. $E=m c^{2}$, to calculate the energy equivalent of the given mass.

Answer (a) We know that

$ \text { Applying } \begin{aligned} 1 amu & =1 u=1.67 \times 10^{-27} kg \\ E & =m c^{2} \\ \text { Energy } & =E=(1.67 \times 10^{-27})(3 \times 10^{8})^{2} J \\ & =1.67 \times 9 \times 10^{-11} J \\ E & =\frac{1.67 \times 9 \times 10^{-11}}{1.6 \times 10^{-13}} MeV=939.4 MeV \approx 931.5 MeV \end{aligned} $

(b) The dimensionally correct relation is

$1 amu \times c^{2}=1 u \times c^{2}=931.5 MeV$