Waves
Multiple Choice Questions (MCQs)
1. Water waves produced by a motorboat sailing in water are
(a) neither longitudinal nor transverse
(b) both longitudinal and transverse
(c) only longitudinal
(d) only transverse
Show Answer
Answer (b) Water waves produced by a motorboat sailing in water are both longitudinal and transverse, because the waves, produce transverse as well as lateral vibrations in the particles of the medium.
-
(a) Water waves produced by a motorboat sailing in water are not “neither longitudinal nor transverse” because they involve both types of vibrations: longitudinal (parallel to the direction of wave propagation) and transverse (perpendicular to the direction of wave propagation).
-
(c) Water waves produced by a motorboat sailing in water are not “only longitudinal” because they also involve transverse vibrations, where the particles of the medium move perpendicular to the direction of wave propagation.
-
(d) Water waves produced by a motorboat sailing in water are not “only transverse” because they also involve longitudinal vibrations, where the particles of the medium move parallel to the direction of wave propagation.
2. Sound waves of wavelength
(a)
(b)
(c)
(d)
Show Answer
Answer
(c) Let the frequency in the first medium is
So,
So,
-
Option (a)
-
Option (b)
-
Option (d)
3. Speed of sound wave in air
(a) is independent of temperature
(b) increases with pressure
(c) increases with increase in humidity
(d) decreases with increase in humidity
Show Answer
Answer (c) Due to presence of moisture density of air decreases.
We know that speed of sound in air is given by
For air
where
As
Hence, speed of sound wave in air increases with increase in humidity.
-
(a) The speed of sound in air is not independent of temperature. In fact, it increases with an increase in temperature because the speed of sound is proportional to the square root of the absolute temperature of the air.
-
(b) The speed of sound in air is not significantly affected by pressure under normal atmospheric conditions because both the pressure and density of air change proportionally with altitude, leaving the speed of sound relatively constant.
-
(d) The speed of sound does not decrease with an increase in humidity. As explained, the presence of moisture decreases the density of air, which in turn increases the speed of sound.
4. Change in temperature of the medium changes
(a) frequency of sound waves
(b) amplitude of sound waves
(c) wavelength of sound waves
(d) loudness of sound waves
Show Answer
Answer
(c) Speed of sound wave in a medium
As,
where
Frequency
As does not change, so wavelength
-
(a) Frequency of sound waves: The frequency of a sound wave is determined by the source of the sound and does not change with the temperature of the medium. The temperature affects the speed of sound, but the frequency remains constant.
-
(b) Amplitude of sound waves: The amplitude of a sound wave is related to the energy and intensity of the wave, which are influenced by the source of the sound and the medium’s properties, but not directly by the temperature of the medium.
-
(d) Loudness of sound waves: Loudness is a perceptual characteristic related to the amplitude and intensity of the sound wave. While temperature can affect the propagation of sound and potentially its perceived loudness due to changes in air density and absorption, it does not directly change the loudness of the sound wave itself.
5. With propagation of longitudinal waves through a medium, the quantity transmitted is
(a) matter
(b) energy
(c) energy and matter
(d) energy, matter and momentum
Show Answer
Answer (b) Propagation of longitudinal waves through a medium leads to transmission of energy through the medium without matter being transmitted.
There is no movement of matter (mass) and hence momentum.
-
(a) Matter: Longitudinal waves do not transmit matter through the medium; they only cause particles of the medium to oscillate back and forth around their equilibrium positions without any net movement of matter.
-
(c) Energy and matter: While longitudinal waves do transmit energy, they do not result in the net movement of matter through the medium. The particles of the medium only oscillate around their equilibrium positions.
-
(d) Energy, matter and momentum: Longitudinal waves transmit energy but do not cause a net movement of matter or momentum through the medium. The particles oscillate back and forth, but there is no overall transfer of matter or momentum.
6. Which of the following statements are true for wave motion?
(a) Mechanical transverse waves can propagate through all mediums
(b) Longitudinal waves can propagate through solids only
(c) Mechanical transverse waves can propagate through solids only
(d) Longitudinal waves can propagate through vacuum
Show Answer
Answer (c) When mechanical transverse wave propagates through a medium, the constituent of the medium oscillate perpendicular to wave motion causing change in shape. That is each, element of the medium is subjected to shearing stress. Solids and strings have shear modulus, that is why, sustain shearing stress.
Fluids have no shape of, their own, they yield to shearing stress. This is why transverse waves are possible in solids and strings but not in fluids.
-
(a) Mechanical transverse waves can propagate through all mediums: This is incorrect because mechanical transverse waves require a medium that can sustain shearing stress. Solids and strings can sustain shearing stress due to their shear modulus, but fluids (liquids and gases) cannot. Therefore, mechanical transverse waves cannot propagate through all mediums, particularly not through fluids.
-
(b) Longitudinal waves can propagate through solids only: This is incorrect because longitudinal waves involve the oscillation of particles in the direction of wave propagation, which results in compressions and rarefactions. These waves can propagate through solids, liquids, and gases, as all these mediums can support compressional stress.
-
(d) Longitudinal waves can propagate through vacuum: This is incorrect because longitudinal waves are mechanical waves that require a medium to propagate. In a vacuum, there are no particles to oscillate and transmit the wave, so longitudinal waves cannot propagate through a vacuum.
7. A sound wave is passing through air column in the form of compression and rarefaction. In consecutive compressions and rarefactions,
(a) density remains constant
(b) Boyle’s law is obeyed
(c) bulk modulus of air oscillates
(d) there is no transfer of heat
Show Answer
Answer (d) (a) Due to compression and rarefactions density of the medium (air) changes. At compressed regions density is maximum and at rarefactions density is minimum
(b) As density is changing, so Boyle’s law is not obeyed
(c) Bulk modulus remains same
(d) The time of compression and rarefaction is too small i.e., we can assume adiabatic process and hence no transfer of heat
-
(a) Due to compression and rarefactions density of the medium (air) changes. At compressed regions density is maximum and at rarefactions density is minimum.
-
(b) As density is changing, so Boyle’s law is not obeyed.
-
(c) Bulk modulus remains same.
8. Equation of a plane progressive wave is given by
(a)
(b)
(c)
(d)
Show Answer
Thinking Process
Due to reflection from a denser medium there is a phase change of
Answer (b) Amplitude of reflected wave
Given equation of incident wave
Equation of reflected wave is
[
So,
-
Option (a): The amplitude of the reflected wave is not correctly adjusted. The given amplitude is 0.6, but it should be
-
Option (c): The amplitude is correctly adjusted to 0.4, but the phase change of
-
Option (d): The amplitude is correctly adjusted to 0.4, but the direction of propagation is not reversed. The correct equation should have a positive sign in the argument of the sine function to indicate the reversal of direction.
9. A string of mass
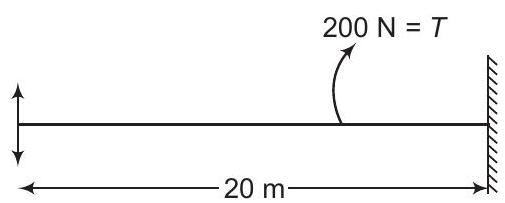
(a)
(b)
(c)
(d) data given is insufficient
Show Answer
Answer (b)
Mass
-
Option (a)
-
Option (c)
-
Option (d) data given is insufficient: This option is incorrect because the given data (mass of the string, tension, and length of the string) is sufficient to calculate the wave speed and the time it takes for the disturbance to travel the length of the string. The problem provides all necessary information to determine the correct answer.
10. A train whistling at constant frequency is moving towards a station at a constant speed

Show Answer
Thinking Process
The observed frequency is apparent frequency due to Doppler shift.
Answer
(c) Let the original frequency of the source is
As observer is stationary
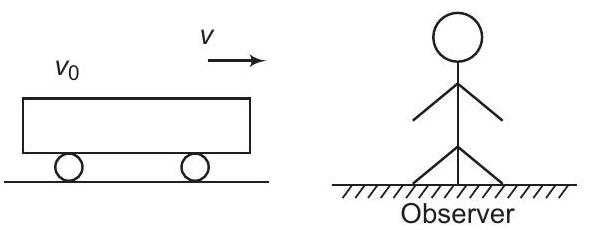
Apparent frequency
[when train is approaching]
When the train is going away from the observer
Apparent frequency
Hence, the expected curve is (c).
-
Option (a): This option suggests a constant frequency over time, which is incorrect because the Doppler effect causes a change in frequency as the train approaches and then recedes from the observer. The frequency should increase as the train approaches and decrease as it moves away.
-
Option (b): This option suggests a linear change in frequency, which is incorrect because the Doppler effect results in a sudden change in frequency at the moment the train passes the observer. The frequency should not change linearly but rather exhibit a sharp transition.
-
Option (d): This option suggests a symmetrical curve with a smooth transition, which is incorrect because the Doppler effect causes an abrupt change in frequency when the train passes the observer. The frequency should show a distinct jump rather than a smooth curve.
Multiple Choice Questions (More Than One Options)
11. A transverse harmonic wave on a string is described by
where
(a) the wave is travelling from right to left
(b) the speed of the wave is
(c) frequency of the wave is
(d) the least distance between two successive crests in the wave is
Show Answer
Thinking Process
To find the characteristic parameters associated with a wave, compare the given equation of the wave with a standard equation.
Answer
Given equation is
Compare the equation with the standard form.
(a) As the equation involves positive sign with
(b) Given
(c)
(d)
Hence, least distance between two successive crests
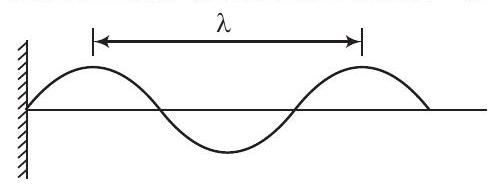
- Option (d) is incorrect: The least distance between two successive crests in the wave is given by the wavelength (\lambda). From the calculations, (\lambda = 3.48 , \text{cm}), not (2.5 , \text{cm}). Therefore, the least distance between two successive crests is not (2.5 , \text{cm}).
12. The displacement of a string is given by
where
(a) It represents a progressive wave of frequency
(b) It represents a stationary wave of frequency
(c) It is the result superposition of two waves of wavelength
(d) Amplitude of this wave is constant
Show Answer
Answer (b, c)
Given equation is
(a) Comparing with a standard equation of stationary wave
Clearly, the given equation belongs to stationary wave. Hence, option (a) is not correct.
(b) By comparing,
(c)
(d) Since in stationary wave, all particles of the medium execute SHM with varying amplitude ’nodes.
-
(a) It represents a progressive wave of frequency
The given equation ( y(x, t) = 0.06 \sin \left( \frac{2 \pi x}{3} \right) \cos (120 \pi t) ) matches the form of a stationary wave equation ( y(x, t) = a \sin (kx) \cos (\omega t) ). A progressive wave would have the form ( y(x, t) = A \sin (kx - \omega t) ) or ( y(x, t) = A \sin (kx + \omega t) ). Therefore, the given equation does not represent a progressive wave.
-
(d) Amplitude of this wave is constant
In a stationary wave, the amplitude varies along the length of the string. The amplitude is zero at the nodes and maximum at the antinodes. The given equation ( y(x, t) = 0.06 \sin \left( \frac{2 \pi x}{3} \right) \cos (120 \pi t) ) shows that the amplitude depends on the position ( x ) (specifically, it is ( 0.06 \sin \left( \frac{2 \pi x}{3} \right) )), indicating that the amplitude is not constant.
13. Speed of sound wave in a fluid depends upon
(a) directly on density of the medium
(b) square of Bulk modulus of the medium
(c) inversly on the square root of density
(d) directly on the square root of bulk modulus of the medium
Show Answer
Answer
(c,
Speed of sound waves in a fluid is given by
Clearly,
and
-
(a) directly on density of the medium: This is incorrect because the speed of sound in a fluid is inversely proportional to the square root of the density, not directly proportional to the density. If the density increases, the speed of sound decreases.
-
(b) square of Bulk modulus of the medium: This is incorrect because the speed of sound in a fluid is directly proportional to the square root of the Bulk modulus, not the square of the Bulk modulus. If the Bulk modulus increases, the speed of sound increases, but not as the square of the Bulk modulus.
14. During propagation of a plane progressive mechanical wave,
(a) all the particles are vibrating in the same phase
(b) amplitude of all the particles is equal
(c) particles of the medium executes SHM
(d) wave velocity depends upon the nature of the medium
Show Answer
Answer
(
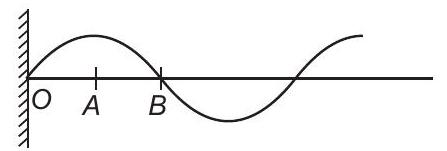
During propagation of a plane progressive mechanical wave, like shown in the diagram, amplitude of all the particles is equal.
(i) Clearly, the particles
(ii) Particles of the wave shown in the figure are having up and down SHM.
(iii) For a progressive wave propagating in a fluid.
Hence,
As
- Reason why option (a) is incorrect: During the propagation of a plane progressive mechanical wave, not all particles are vibrating in the same phase. Different particles are at different points in their cycles of motion, as indicated by the particles O, A, and B having different phases in the diagram.
15. The transverse displacement of a string (clamped at its both ends) is given by
All the points on the string between two consecutive nodes vibrate with
(a) same frequency
(b) same phase
(c) same energy
(d) different amplitude
Show Answer
Answer
Given equation is
Comparing with standard equation of stationary wave
It is represented by diagram.
where
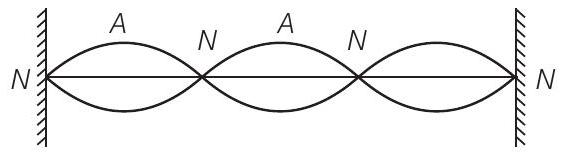
(a) Clearly, frequency is common for all the points.
(b) Consider all the particles between two nodes they are having same phase of
(c) and (d) But are having different amplitudes of
- Option (c) is incorrect because the points between two consecutive nodes have different amplitudes given by (0.06 \sin \left(\frac{2 \pi}{3} x\right)). Since energy is proportional to the square of the amplitude, different amplitudes result in different energies.
16. A train, standing in a station yard, blows a whistle of frequency
(a) the frequency of sound as heard by an observer standing on the platform is
(b) the speed of sound for the observer standing on the platform is
(c) the frequency of sound as heard by the observer standing on the platform will increase
(d) the frequency of sound as heard by the observer standing on the platform will decrease
Show Answer
Thinking Process
When the wind is blowing in the same direction as that of sound wave then net speed of the wave is sum of speed of sound wave and speed of the wind.
Answer
(
Given,
Speed of wind
(a) As both source and observer are stationary, hence frequency observed will be same as natural frequency
(b) The speed of sound
(c) and (d) There will be no effect on frequency,because there is no relative motion between source and observer hence (c),(d) are incorrect.
-
(c) The frequency of sound as heard by the observer standing on the platform will increase: This is incorrect because there is no relative motion between the source (train) and the observer (standing on the platform). The wind affects the speed of sound but not the frequency when both the source and observer are stationary.
-
(d) The frequency of sound as heard by the observer standing on the platform will decrease: This is incorrect for the same reason as (c). There is no relative motion between the source and the observer, so the frequency remains unchanged.
17. Which of the following statement are true for a stationary waves?
(a) Every particle has a fixed amplitude which is different from the amplitude of its nearest particle
(b) All the particles cross their mean position at the same time
(c) All the particles are oscillating with same amplitude
(d) There is no net transfer of energy across any plane
(e) There are some particles which are always at rest
Show Answer
Answer
Consider the equation of a stationary wave
(a) clearly every particle at
(b) for mean position
Hence, for a fixed value of
(c) amplitude of all the particles are a
(d) the energy is a stationary wave is confined between two nodes
(e) particles at different nodes are always at rest.
- (c) The amplitude of all the particles is (a \sin (kx)), which is different for different particles at different values of (x). Therefore, not all particles are oscillating with the same amplitude.
Very Short Answer Type Questions
18. A sonometer wire is vibrating in resonance with a tuning fork. Keeping the tension applied same, the length of the wire is doubled. Under what conditions would the tuning fork still be is resonance with the wire?
Show Answer
Answer
Wire of twice the length vibrates in its second harmonic. Thus, if the tuning fork resonates at
The sonometer frequency is given by
Now, as it vibrates with length
When length is doubled, then
Dividing Eq. (i) by Eq. (ii), we get
To keep the resonance
Hence, when the wire is doubled the number of loops also get doubled to produce the resonance. That is it resonates in second harmonic.
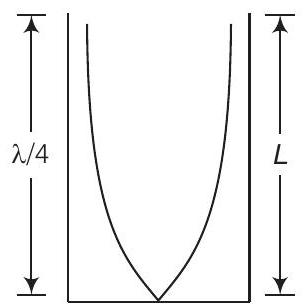
19. An organ pipe of length
Show Answer
Thinking Process
We should not confuse between pressure wave and displacement wave. By considering any type of wave outcome will be same.
Answer Consider the situation shown in the diagram
As the organ pipe is open at both ends, hence for first harmonic
where
For pipe closed at one end
c for first harmonic
Hence,
20. A tuning fork
Show Answer
Answer
Frequency of tuning fork
Probable frequency of tuning fork
when
If it is
If it is
Note For production of beats frequencies of the two tuning forks must be nearly equal i.e., slight difference in frequencies.
21. The displacement of an elastic wave is given by the function
Show Answer
Answer
Given, displacement of an elastic wave
On dividing Eq. (ii) by Eq. (i)
Also,
Hence,
where
Hence, amplitude
22. A sitar wire is replaced by another wire of same length and material but of three times the earlier radius. If the tension in the wire remains the same, by what factor will the frequency change?
Show Answer
Thinking Process
In a sitar wire, the vibration is assumed to be similar as a wire fixed at both ends.
Answer Frequency of vibrations produced by a stretched wire
23. At what temperatures
Show Answer
Answer
We know that speed of sound in air
24. When two waves of almost equal frequencies
Show Answer
Thinking Process
When two waves of almost equal frequencies interfere, they are producing beats.
Answer Let,
Beat frequency
Time period of beats
Short Answer Type Questions
25. A steel wire has a length of
Show Answer
Answer Given, length of the wire
Mass of wire
Tension
Speed of transverse wave
26. A pipe
Show Answer
Answer Length of pipe
Hence, 3rd harmonic node of the pipe is resonantly excited by the source of given frequency.
27. A train standing at the outer signal of a railway station blows a whistle of frequency
Show Answer
Answer As the source (train) is moving towards the observer (platform) hence apparent frequency observed is more than the natural frequency.
Frequency of whistle
Speed of train
Velocity of sound in air
Apparent frequency when source is moving
28. The wave pattern on a stretched string is shown in figure. Interpret what kind of wave this is and find its wavelength.
Show Answer
Answer We have to observe the displacement and position of different points, then accordingly nature of two wave is decided.
Points on positions
29. The pattern of standing waves formed on a stretched string at two instants of time are shown in figure. The velocity of two waves superimposing to form stationary waves is
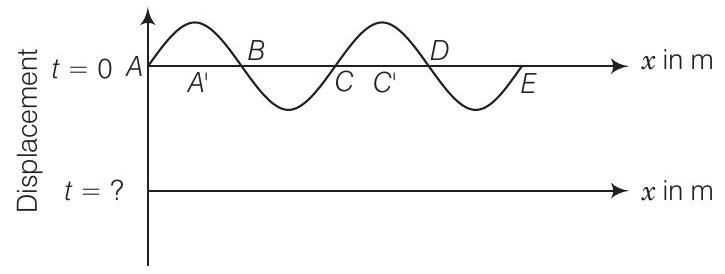
(a) Calculate the time at which the second curve is plotted.
(b) Mark nodes and antinodes on the curve.
(c) Calculate the distance between
Show Answer
Answer
Given, frequency of the wave
Time period
(a) Time taken to pass through mean position is
(b) Nodes are
(c) It is clear from the diagram
30. A tuning fork vibrating with a frequency of
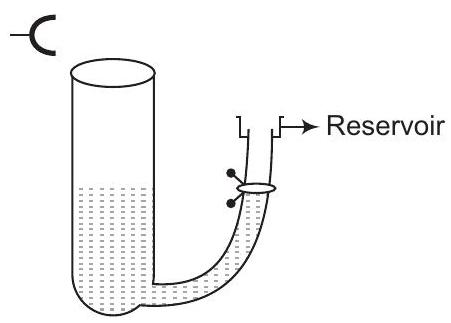
(a) speed of sound in air at room temperature.
(b) speed of sound in air at
(c) if the water in the tube is replaced with mercury, will there be any difference in your observations?
Show Answer
Thinking Process
The pipe partially filled with water, acts as closed organ pipe. According to this, we will find associated frequencies.
Answer
Consider the diagram frequency of tuning fork
For observation of first maxima of intensity
(a)
[for closed pipe]
(b) We know that
where temperature
(c) Resonance will be observed at
31. Show that when a string fixed at its two ends vibrates in 1 loop, 2 loops, 3 loops and 4 loops, the frequencies are in the ratio
Show Answer
Answer
Let, there are
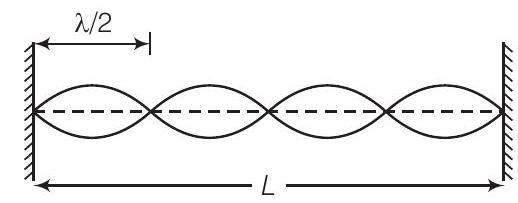
Length corresponding each loop is
Now, we can write
Long Answer Type Questions
32. The earth has a radius of
Assume that the
Show Answer
Answer
Speed of wave in solid
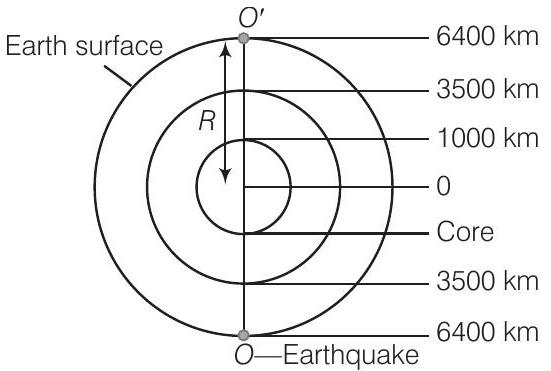
Speed of wave in liquid
Required time
As we are considering at diametrically opposite point, hence there is a multiplication of 2.
33. If
Show Answer
Answer We know that rms speed of molecules of a gas
where
Speed of sound wave in gas
On dividing Eq. (i) by Eq. (ii), we get
where
Hence,
34. Given below are some functions of
(i)
(ii)
(iii)
(iv)
State which of these represent
(a) a travelling wave along-
(b) a stationary wave
(c) beats
(d) a travelling wave along-
Given reasons for your answers.
Show Answer
Thinking Process
To predict the nature of wave we have to compare with standard equations.
Answer
(a) The equation
(b) The equation
(c) As the equation
(d) As the equation
Note We must not confuse with sign connected with
35. In the given progressive wave
(a) amplitude?
(b) wavelength?
(c) frequency?
(d) wave velocity?
(e) particle velocity amplitude?
Show Answer
Answer Standard equation of a progressive wave is given by
This is travelling along positive
Given equation is
Comparing with the standard equation
(a) Amplitude
(b)
(c)
(d) Wave velocity
(e)
From Eq. (i),
For particle velocity amplitude
Which will be for
36. For the harmonic travelling wave
(a)
(b)
(c)
(d)
(e) What is the phase difference between the oscillation of a particle located at
Show Answer
Answer Given, wave functions are
Now, standard equation of a travelling wave can be written as
On comparing with above equation, we get
Path difference
(a) Phase difference
(b)
(c)
(d)
(e)
Again, at










