Kinetic theory
Multiple Choice Questions (MCQs)
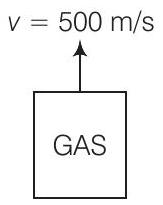
1. A cubic vessel (with face horizontal + vertical) contains an ideal gas at NTP. The vessel is being carried by a rocket which is moving at a speed of
(a) remains the same because
(b) remains the same because motion of the vessel as a whole does not affect the relative motion of the gas molecules and the walls
(c) will increase by a factor equal to
(d) will be different on the top wall and bottom wall of the vessel
Show Answer
Thinking Process
This phenomenon is based on the concept of relative motion that is when collision takes place, it is the relative velocity which changes.
Answer (b) As the motion of the vessel as a whole does not effect the relative motion of the gas molecules with respect to the walls of the vessel, hence pressure of the gas inside the vessel, as observed by us, on the ground remains the same.
-
(a) The statement is incorrect because the comparison between the rocket’s speed and the root mean square speed (
-
(c) This option is incorrect because it suggests that the pressure will increase by a factor involving the square of the rocket’s speed and the original mean square velocity of the gas. However, the pressure of an ideal gas is dependent on the temperature and volume, not on the external motion of the vessel. The relative motion of the gas molecules with respect to the walls of the vessel remains unchanged, so the pressure does not increase by this factor.
-
(d) This option is incorrect because it implies that the pressure will be different on the top and bottom walls of the vessel due to the rocket’s vertical motion. However, the pressure inside the vessel is isotropic (the same in all directions) and is determined by the collisions of gas molecules with the walls, which are unaffected by the uniform motion of the vessel.
2. 1 mole of an ideal gas is contained in a cubical volume
(a) the pressure on
(b) the pressure on all the faces will the equal
(c) the pressure of
(d) the pressure on
Show Answer
Answer
(d) In an ideal gas, when a molecule collides elastically with a wall, the momentum transferred to each molecule will be twice the magnitude of its normal momentum. For the face
-
(a) the pressure on
-
(b) the pressure on all the faces will be equal: This is incorrect because the face
-
(c) the pressure of
3. Boyle’s law is applicable for an
(a) adiabatic process
(b) isothermal process
(c) isobaric process
(d) isochoric process
Show Answer
Answer
(b) Boyle’s law is applicable when temperature is constant
i.e.,
i.e.,
[where,
So, this process can be called as isothermal process.
-
Adiabatic process: In an adiabatic process, there is no heat exchange with the surroundings, and the temperature of the gas changes. Boyle’s law requires the temperature to remain constant, which is not the case in an adiabatic process.
-
Isobaric process: In an isobaric process, the pressure remains constant. Boyle’s law describes the relationship between pressure and volume at a constant temperature, not at a constant pressure.
-
Isochoric process: In an isochoric process, the volume remains constant. Boyle’s law involves changes in volume and pressure while keeping the temperature constant, which is not applicable when the volume is fixed.
4. A cylinder containing an ideal gas is in vertical position and has a piston of mass
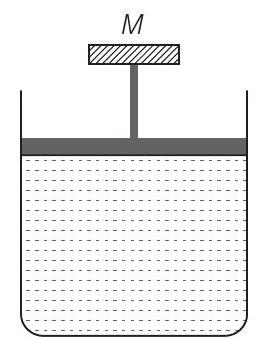
(a) both
(b) only
(c)
(d)
Show Answer
Answer
(c) Consider the diagram where an ideal gas is contained in a cylinder, having a piston of mass
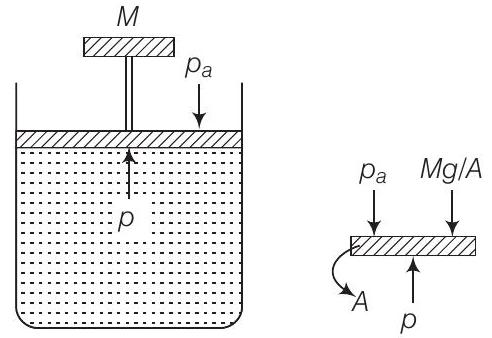
The pressure inside the gas will be
where,
Hence,
When temperature increases
as
-
Option (a): This option is incorrect because it states that both pressure ( p ) and volume ( V ) of the gas will change. However, in the given scenario, the pressure ( p ) remains constant due to the balance of forces on the piston (atmospheric pressure plus the weight of the piston). Only the volume ( V ) changes as the temperature increases, according to the ideal gas law ( pV = nRT ).
-
Option (b): This option is incorrect because it states that only pressure ( p ) will increase according to Charles’ law. Charles’ law actually states that the volume of a gas is directly proportional to its temperature at constant pressure. In this scenario, the pressure remains constant, and it is the volume ( V ) that increases with temperature, not the pressure.
-
Option (d): This option is incorrect because it states that pressure ( p ) will change but not volume ( V ). In the given setup, the pressure ( p ) remains constant due to the balance of forces on the piston. As the temperature increases, the volume ( V ) must increase to maintain the relationship described by the ideal gas law ( pV = nRT ).
5. Volume versus temperature graphs for a given mass of an ideal gas are shown in figure. At two different values of constant pressure. What can be inferred about relation between
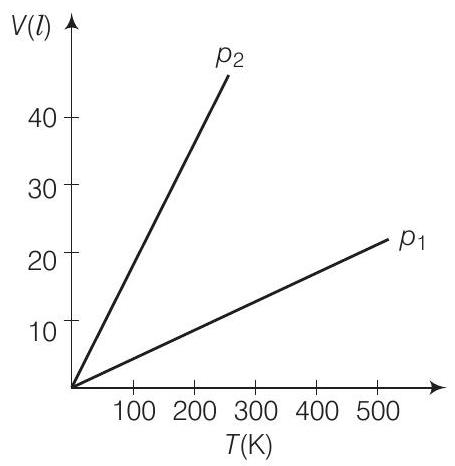
(a)
(b)
(c)
(d) Data is insufficient
Show Answer
Thinking Process
To find the required relation, we have to consider slope of the
Answer (a) We know for an ideal gas,
where,
-
Option (b)
-
Option (c)
-
Option (d) Data is insufficient: This option is incorrect because the given information and the ideal gas law provide enough data to determine the relationship between ( p_1 ) and ( p_2 ). The slopes of the graphs and the derived relationship ( p \propto \frac{1}{m} ) are sufficient to conclude that ( p_1 > p_2 ).
6. 1 mole of
(a) same as the pressure initially
(b) 2 times the pressure initially
(c) 10 times the pressure initially
(d) 20 times the pressure initially
Show Answer
Answer (d) Consider the diagram, when the molecules breaks into atoms, the number of moles would become twice.
Now, by ideal gas equation
As volume
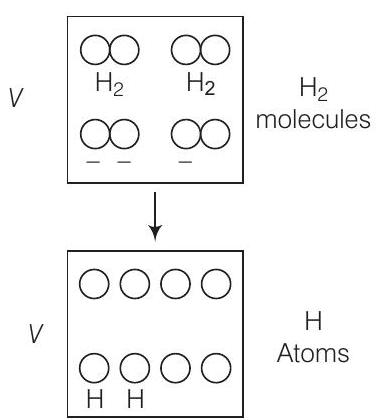
As gases breaks number of moles becomes twice of initial, so
So,
Hence, final pressure of the gas would be 20 times the pressure initially.
-
Option (a) same as the pressure initially: This option is incorrect because when the gas is heated and the
-
Option (b) 2 times the pressure initially: This option is incorrect because although the number of moles doubles when
-
Option (c) 10 times the pressure initially: This option is incorrect because it only accounts for the increase in temperature by a factor of 10. It does not consider the doubling of the number of moles when
7. A vessel of volume
(a)
(b)
(c) neither
(d)
Show Answer
Answer
(b) For a function
For each function
-
(a)
-
(c) neither
-
(d)
8. An inflated rubber balloon contains one mole of an ideal gas, has a pressure
(a)
(b)
(c) less than
(d) between
Show Answer
Answer
(d) We know for an ideal gas,
As number of moles of the gas remains fixed, hence, we can write
Hence, final pressure
-
Option (a)
-
Option (b)
-
Option (c) less than
Multiple Choice Questions (More Than One Options)
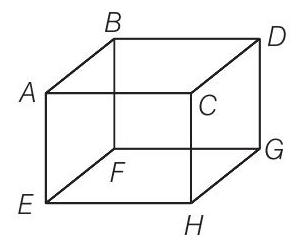
9. A B C D E F G H is a hollow cube made of an insulator (figure) face
The usual kinetic theory expression for pressure
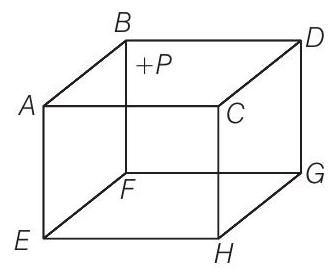
(a) will be valid
(b) will not be valid, since the ions would experience forces other than due to collisions with the walls
(c) will not be valid, since collisions with walls would not be elastic
(d) will not be valid because isotropy is lost
Show Answer
Thinking Process
As ionised hydrogen is present inside the cube, they are having charge. Now, due to presence of positive charge on the surface
Answer
Due to presence of external positive charge on the face
-
(a) will be valid: This option is incorrect because the presence of an external positive charge on face (ABCD) introduces additional electrostatic forces on the ions inside the cube. The usual kinetic theory expression for pressure assumes that the only forces acting on the particles are due to collisions with the walls, which is not the case here.
-
(c) will not be valid, since collisions with walls would not be elastic: This option is incorrect because the problem does not specify any reason for the collisions with the walls to be inelastic. The presence of an external charge affects the forces on the ions but does not necessarily imply that the collisions with the walls are inelastic.
10. Diatomic molecules like hydrogen have energies due to both translational as well as rotational motion. From the equation in kinetic theory
(a) the total energy per unit volume
(b) only the translational part of energy because rotational energy is very small compared to the translational energy
(c) only the translational part of the energy because during collisions with the wall pressure relates to change in linear momentum
(d) the translational part of the energy because rotational energies of molecules can be of either sign and its average over all the molecules is zero
Show Answer
Answer (c) According to kinetic theory, we assume the walls only exert perpendicular forces on molecules. They do not exert any parallel force, hence there will not be any type of rotation present.
The wall produces only change in translational motion.
Hence, in the equation
-
(a) the total energy per unit volume: This option is incorrect because the equation ( pV = \frac{2}{3} E ) specifically relates to the translational kinetic energy of the gas molecules, not the total energy which would include rotational and possibly vibrational energies as well.
-
(b) only the translational part of energy because rotational energy is very small compared to the translational energy: This option is incorrect because the reason given is not accurate. The rotational energy is not necessarily very small compared to the translational energy. The correct reason is that the equation ( pV = \frac{2}{3} E ) is derived considering only the translational kinetic energy due to the change in linear momentum during collisions with the walls.
-
(d) the translational part of the energy because rotational energies of molecules can be of either sign and its average over all the molecules is zero: This option is incorrect because rotational energies cannot be of either sign; they are always positive. The correct reason is that the equation ( pV = \frac{2}{3} E ) is derived from the translational kinetic energy, which is directly related to the pressure and volume through the change in linear momentum during collisions with the walls.
11. In a diatomic molecule, the rotational energy at a given temperature
(a) obeys Maxwell’s distribution
(b) have the same value for all molecules
(c) equals the translational kinetic energy for each molecule
(d) is (2/3)rd the translational kinetic energy for each molecule
Show Answer
Answer
Consider a diatomic molecule as shown in the diagram.
The total energy associated with the molecule is
This above expression contains translational kinetic energy
The number of independent terms in the above expression is 5.
As we can predict velocities of molecules by Maxwell’s distribution, hence the above expression also obeys Maxwell’s distribution.
-
(b) have the same value for all molecules: This option is incorrect because the rotational energy of molecules follows a distribution (Maxwell-Boltzmann distribution) and does not have the same value for all molecules. The energy levels are quantized and can vary among different molecules.
-
(c) equals the translational kinetic energy for each molecule: This option is incorrect because the rotational energy is not equal to the translational kinetic energy. In a diatomic molecule, the rotational energy is a fraction of the translational kinetic energy, specifically (\frac{2}{3}) of the translational kinetic energy, as derived from the degrees of freedom associated with the molecule.
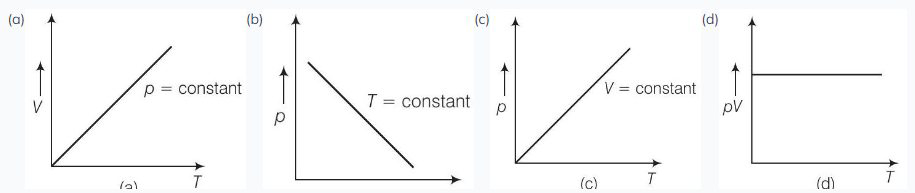
12. Which of the following diagrams (figure) depicts ideal gas behaviour?
Show Answer
Answer
We know that ideal gas equation is
(a) When pressure,
(b) When
From (i)
So, the graph is rectangular hyperbola.
(c) When
From (i)
So, the graph is straight line passes through the origin.
(d) From (i)
So, (d) is not correct.
-
Option (b): When temperature ( T ) is constant, the relationship ( pV = \text{constant} ) should form a rectangular hyperbola. However, the graph in option (b) does not depict a rectangular hyperbola, hence it does not represent ideal gas behavior under isothermal conditions.
-
Option (d): The relationship ( \frac{pV}{T} = \text{constant} ) implies that the graph should pass through the origin. However, the graph in option (d) does not pass through the origin, hence it does not represent ideal gas behavior.
13. When an ideal gas is compressed adiabatically, its temperature rises the molecules on the average have more kinetic energy than before. The kinetic energy increases,
(a) because of collisions with moving parts of the wall only
(b) because of collisions with the entire wall
(c) because the molecules gets accelerated in their motion inside the volume
(d) because of redistribution of energy amongest the molecules
Show Answer
Thinking Process
The elastic collisions of the molecules with a moving part of two system increases their energy.
Answer (a) When the gas is compressed adiabatically, the total work done on the gas increases its internal energy which in turn increase the KE of gas molecules and hence, the collisions between molecules also increases.
-
(b) The kinetic energy does not increase because of collisions with the entire wall. In an adiabatic process, there is no heat exchange with the surroundings, so the increase in kinetic energy is due to the work done on the gas, not because of collisions with the entire wall.
-
(c) The kinetic energy does not increase because the molecules get accelerated in their motion inside the volume. The acceleration of molecules is a result of the increase in kinetic energy, not the cause. The cause is the work done on the gas during compression.
-
(d) The kinetic energy does not increase because of the redistribution of energy amongst the molecules. Redistribution of energy among molecules does not change the total kinetic energy; it only changes the distribution of energy. The increase in kinetic energy is due to the work done on the gas during adiabatic compression.
Very Short Answer Type Questions
14. Calculate the number of atoms in
Show Answer
Answer We know that,
Given,
Now,
15. The volume of a given mass of a gas at
Show Answer
Answer We have to convert the given temperatures in kelvin . If pressure of a given mass of the gas is kept constant, then
Note To apply ideal gas equation, we must convert the given temperature in kelvin.
16. The molecules of a given mass of a gas have root mean square speeds of
Show Answer
Answer We know that for a given mass of a gas
where,
Clearly,
As
Given,
from eq (i)
17. Two molecules of a gas have speeds of
Show Answer
Answer
For
where
For two molecules,
Given,
and
18. A gas mixture consists of 2.0 moles of oxygen and 4.0 moles of neon at temperature
Show Answer
Thinking Process
To find exact value of total energy for a given molecule of a gas, we must know the number of degree of freedom associated with the molecules of the gas.
Answer
Energy (total internal) per mole of the gas
For 2 moles of the gas total internal energy
Neon (Ne) is a monoatomic gas having 3 degrees of freedom.
We have 4 moles of
Hence,
19. Calculate the ratio of the mean free paths of the molecules of two gases having molecular diameters
Show Answer
Answer Mean free path of a molecule is given by
where,
Now, we can write
Given,
As
Hence,
Short Answer Type Questions
20. The container shown in figure has two chambers, separated by a partition, of volumes
Show Answer
Answer Consider the diagram,
Given,
For chamber 1,
For chamber 2,
When the partition is removed the gases get mixed without any loss of energy. The mixture now attains a common equilibrium pressure and the total volume of the system is sum of the volume of individual chambers
So,
From kinetic theory of gases,
For
For
For
Total energy is
From the abvne relation,
21. A gas mixture consists of molecules of
Show Answer
Answer (a) The average KE will be the same, as conditions of temperature and pressure are the same.
Now as,
where,
Clearly,
(b) As k = Boltzmann constant
But
OR
22. We have
Show Answer
Thinking Process
For justification of assuming the ideal gas law, the molecular volume and the volume occupied of the ideal gas is compared. If both matches, then law holds good otherwise not.
Answer
Assuming hydrogen molecules as spheres of radius
So,
The volume of hydrogen molecules
Molecules of
Now, if ideal gas law is considered to be constant.
Hence, on compression the volume of the gas is of the order of the molecular volume [form Eq.(i) and Eq.(ii)]. The intermolecular forces will play role and the gas will deviate from ideal gas behaviour.
23. When air is pumped into a cycle tyre the volume and pressure of the air in the tyre both are increased. What about Boyle’s law in this case?
Show Answer
Answer When air is pumped, more molecules are pumped and Boyle’s law is stated for situation where number of molecules remains constant.
In this case, as the number of air molecules keep increasing. Hence, this is a case of variable mass. Boyle’s law (and even Charle’s law) is only applicable in situations, where number of gas molecules remains fixed.
Hence, in this case Boyle’s law is not applicable.
24. A balloon has 5.0 mole of helium at
(a) the number of atoms of helium in the balloon.
(b) the total internal energy of the system.
Show Answer
Thinking Process
Energy associated with a monoatomic molecule is
Answer
Given, number of moles of helium
(a) Hence, number of atoms (He is monoatomic)
(b) Now, average kinetic energy per molecule
Here,
(It has only 3 degrees of freedom)
25. Calculate the number of degrees of freedom of molecules of hydrogen in 1 cc of hydrogen gas at NTP.
Show Answer
Thinking Process
Total number of degrees of freedom in a thermodynamical system
Answer As given molecules are of hydrogen.
Note Any ideal gas has a molar volume of
26. An insulated container containing monoatomic gas of molar mass
Show Answer
Thinking Process
As the container is suddenly stopped there is no time for exchange of heat in the process.
Answer According to kinetic interpretation of temperature, absolute temperature of a given sample of a gas is proportional to the total translational kinetic energy of its molecules.
Hence, any change in absolute temperature of a gas will contribute to corresponding change in translational KE and vice-versa.
Assuming
Given,
When, the container stops, its total KE is transferred to gas molecules in the form of translational KE, thereby increasing the absolute temperature.
If
Then,
Increase in translational
According to kinetic theory Eqs. (i) and (ii) are equal
Long Answer Type Questions
27. Explain why
(a) there is no atmosphere on moon
(b) there is fall in temperature with altitude
Show Answer
Answer
(a) The moon has small gravitational force (pull) and hence, the escape velocity is small. The value of escape velocity for the moon is
As the moon is in the proximity of the earth as seen from the sun, the moon has the same amount of heat per unit area as that of the earth.
The air molecules have large range of speeds. Even though the rms speed of the air molecules is smaller than the escape velocity on the moon, a significant number of molecules have speed greater than escape velocity and they escape.
Now, rest of the molecules arrange the speed distribution for the equilibrium temperature. Again a significant number of molecules escape as their speed exceed escape speed. Hence, over a long time the moon has lost most of its atmosphere.
(b) As the molecules move higher; their potential energy increases and hence, kinetic energy decreases and hence, temperature reduces.
At greater height more volume is available and gas expands and hence, some cooling takes place.
Note We should not relate temperature directly with potential energy. It is directly related with kinetic energy of the molecules.
28. Consider an ideal gas with following distribution of speeds.
| Speed |
% of molecules |
|---|---|
| 200 | 10 |
| 400 | 20 |
| 600 | 40 |
| 800 | 20 |
| 1000 | 10 |
(a) Calculate
(b) If all the molecules with speed
Show Answer
Thinking Process
In this problem, it is shown that cooling takes place after evaporation.
Answer (a) We know that
This is the rms speed for all molecules collectively.
Now, according to kinetic theory of gasses
(b) If all the molecules with speed
Note After escaping of molecules with speed of
29. Ten small planes are flying at a speed of
Show Answer
Thinking Process
To solve this problem, we have to consider the relaxation time as well as mean free path.
Answer The situation can be considered as the time of relaxation, based on kinetic theory of gases. Mean free path is the distance between two successive collisions, which we will consider here as the distance travelled by the plane before it just avoids the collision safe radius is equivalent to radius of the atom.
Hence, the required time
By putting the given data,
30. A box of
Show Answer
Answer
Given, volume of the box,
Temperature outside
Initial pressure inside the
Final pressure inside the
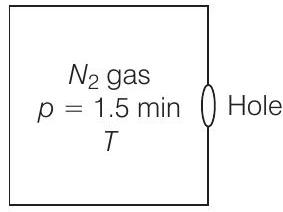
Let area of the wall, number of particles colliding in time
Inside the box,
[According to kinetic theory of gases]
Now
or
If particles collide along hole, they move out. Similarly, outer particles colliding along hole will move in.
If
Then, net particle flow in time
[Temperatures inside and outside the box are equal]
Let
Let
If after time
Now, number of molecules gone out
Putting the values from the data given,
31. Consider a rectangular block of wood moving with a velocity
Show Answer
Thinking Process
If a massive body is moving with respect to a lighter body with velocity
Answer Consider the diagram
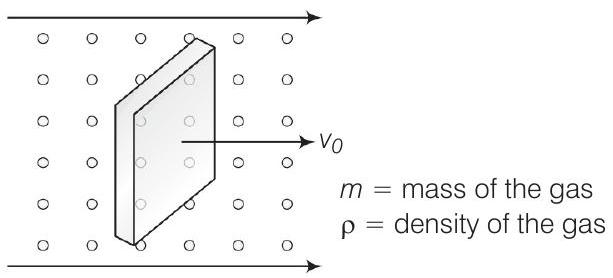
Let
When block is moving with speed
Coming head on, momentum transferred to block per collision
where,
Number of collission in time
Similarly, momentum transferred in time
where we have assumed
[from front]
If
Then, we can write










