Differential Equations
Short Answer Type Questions
1. Find the solution of $\frac{d y}{d x}=2^{y-x}$.
Show Answer
Solution
The given differential equation is
Separating the variables, we get
$ \frac{d y}{d x}=2^{y-x} \Rightarrow \frac{d y}{d x}=\frac{2^{y}}{2^{x}} $
$ \frac{d y}{2^{y}}=\frac{d x}{2^{x}} \Rightarrow 2^{-y} d y=2^{-x} d x $
Integrating both sides, we get
$ \begin{aligned} \int 2^{-y} d y & =\int 2^{-x} d x \\ & \\ \frac{-2^{-y}}{\log 2} & =\frac{-2^{-x}}{\log 2}+c \quad \Rightarrow-2^{-y}=-2^{-x}+c \log 2 \\ \Rightarrow \quad-2^{-y}+2^{-x} & =c \log 2 \\ \Rightarrow \quad 2^{-x}-2^{-y} & =k \quad \quad \quad \text{ [where $c \log$ 2=k ]} \end{aligned} $
2. Find the differential equation of all non vertical lines in a plane.
Show Answer
Solution
Equation of all non vertical lines are $y=m x+c$
Differentiating with respect to $x$, we get $\frac{d y}{d x}=m$
Again differentiating w.r.t. $x$ we have $\frac{d^{2} y}{d x^{2}}=0$
Hence, the required equation is $\frac{d^{2} y}{d x^{2}}=0$.
3. Given that $\frac{d y}{d x}=e^{-2 y}$ and $y=0$ when $x=5$. Find the value of $x$ when $y=3$.
Show Answer
Solution
Given equation is
$ \begin{aligned} \frac{d y}{d x} & =e^{-2 y} \\ \Rightarrow \quad \frac{d y}{e^{-2 y}} & =d x \Rightarrow e^{2 y} \cdot d y=d x \end{aligned} $
Integrating both sides, we get
Put $y=0$ and $x=5$
$ \int e^{2 y} d y=\int d x \Rightarrow \frac{1}{2} e^{2 y}=x+c $
$\Rightarrow \frac{1}{2} e^{0}=5+c \Rightarrow c=\frac{1}{2}-5=-\frac{9}{2}$
$\therefore$ The equation becomes $\frac{1}{2} e^{2 y}=x-\frac{9}{2}$
Now putting $y=3$, we get
$ \frac{1}{2} e^{6}=x-\frac{9}{2} \Rightarrow x=\frac{1}{2} e^{6}+\frac{9}{2} $
Hence the required value of $x=\frac{1}{2}(e^{6}+9)$.
4. Solve the differential equation $(x^{2}-1) \frac{d y}{d x}+2 x y=\frac{1}{x^{2}-1}$.
Show Answer
Solution
Given differential equation is
$ (x^{2}-1) \frac{d y}{d x}+2 x y=\frac{1}{x^{2}-1} $
Dividing by $(x^{2}-1)$, we get
$ \frac{d y}{d x}+\frac{x y}{x^{2}-1}=\frac{}{(x^{2}-1)^{2}} $
It is a linear differential equation of first order and first degree.
$\therefore \quad P=\frac{2 x}{x^{2}-1}$ and $Q=\frac{1}{(x^{2}-1)^{2}}$
Integrating factor I.F. $=e^{\int P d x}=e^{\int \frac{2 x}{x^{2}-1} d x}=e^{\log (x^{2}-1)}=(x^{2}-1)$.
$\therefore$ Solution of the equation is
$ \begin{aligned} & y \times \text{ I.F. }=\int \text{ Q.I.F. } d x+\text{ C } \\ & \Rightarrow y \times(x^{2}-1)=\int \frac{1}{(x^{2}-1)^{2}} \times(x^{2}-1) d x+\text{ C } \\ & \Rightarrow y(x^{2}-1)=\int \frac{1}{x^{2}-1} d x+C \Rightarrow y(x^{2}-1)=\frac{1}{2} \log |\frac{x-1}{x+1}|+C \end{aligned} $
Hence the required solution is $y(x^{2}-1)=\frac{1}{2} \log |\frac{x-1}{x+1}|+C$.
5. Solve the differential equation $\frac{d y}{d x}+2 x y=y$.
Show Answer
Solution
Given equation is $\frac{d y}{d x}+2 x y=y$.
$ \Rightarrow \quad \frac{d y}{d x}=y-2 x y \quad \Rightarrow \frac{d y}{d x}=y(1-2 x) \Rightarrow \frac{d y}{y}=(1-2 x) d x $
Integrating both sides, we have
$ \begin{aligned} & \int \frac{d y}{d y}=\int(1-2 x) d x \Rightarrow \log y=x-2 \cdot \frac{x^{2}}{2}+\log c \\ & \Rightarrow \quad \log y=x-x^{2}+\log c \Rightarrow \log y-\log c=x-x^{2} \\ & \Rightarrow \quad \log \frac{y}{c}=x-x^{2} \Rightarrow \frac{y}{c}=e^{x-x^{2}} \\ & \therefore \quad y=y=c \cdot e^{x-x^{2}} \end{aligned} $
Hence, the required solution is $y=c \cdot e^{x-x^{2}}$.
6. Find the general solution of $\frac{d y}{d x}+a y=e^{m x}$.
Show Answer
Solution
Given equation is $\frac{d y}{d x}+a y=e^{m x}$.
Here, $P=a$ and $Q=e^{m x}$
$\therefore$ I.F $=e^{\int P d x}=e^{\int a \cdot d x}=e^{a x}$.
Solution of equation is $y \times$ I.F $=\int Q$ I.F $d x+c$
$ \begin{matrix} \Rightarrow \quad y \cdot e^{a x}=\int e^{m x} \cdot e^{a x} d x+c \Rightarrow y \cdot e^{a x}=\int e^{(m+a) x} d x+c \\ \Rightarrow \qquad y \cdot e^{a x}=\frac{e^{(m+a) x}}{(m+a)}+c \Rightarrow y=\frac{e^{(m+a) x}}{(m+a)} \cdot e^{-a x}+c \cdot e^{-a x} \\ \therefore \qquad y=\frac{e^{m x}}{(m+a)}+c \cdot e^{-a x} \end{matrix} $
Hence the required solution is $y=\frac{e^{m x}}{(m+a)}+c \cdot e^{-a x}$.
7. Solve the differential equation $\frac{d y}{d x}+1=e^{x+y}$.
Show Answer
Solution
Given that: $\frac{d y}{d x}+1=e^{x+y}$
Put $x+y=t$
$ \begin{matrix} \therefore & 1+\frac{d y}{d x} & =\frac{d t}{d x} \\ & \therefore & \frac{d t}{d x} & =e^{t} \Rightarrow \frac{d t}{e^{t}}=d x \Rightarrow e^{-t} d t=d x \end{matrix} $
Integrating both sides, we have
$ \begin{gathered} \int e^{-t} d t=\int d x \Rightarrow-e^{-t}=x+c \\ \Rightarrow \quad-e^{-(x+y)}=x+c \Rightarrow \frac{-1}{e^{x+y}}=x+c \Rightarrow(x+c) e^{x+y}=-1 \end{gathered} $
Hence, the required solution is $(x+c) \cdot e^{x} \quad y+1=0$.
8. Solve: $y d x-x d y=x^{2} y d x$.
Show Answer
Solution
Given equation is $y d x-x d y=x^{2} y d x$.
$ \begin{aligned} & \Rightarrow \quad y d x-x^{2} y d x=x d y \\ & \Rightarrow \quad y(1-x^{2}) d x=x d y \\ & \Rightarrow \quad(\frac{1-x^{2}}{x}) d x=\frac{d y}{y} \Rightarrow(\frac{1}{x}-x) d x=\frac{d y}{y} \end{aligned} $
Integrating both sides we get
$ \begin{aligned} & \int(\frac{1}{x}-x) d x=\int \frac{d y}{y} \\ \Rightarrow & \log x-\frac{x^{2}}{2}=\log y+\log c \end{aligned} $
$ \begin{aligned} & \Rightarrow \log x-\frac{x^{2}}{2}=\log y c \Rightarrow \log x-\log c=\frac{x^{2}}{2} \Rightarrow \log \frac{x}{y c}=\frac{x^{2}}{2} \\ & \Rightarrow \quad \frac{x}{y c}=e^{x^{2} / 2} \Rightarrow \frac{y c}{x}=e^{-x^{2} / 2} \Rightarrow y c=x e^{-x^{2} / 2} \\ & \therefore \quad y=\frac{1}{c} \cdot x e^{-x^{2} / 2} \Rightarrow y=k x e^{-x^{2} / 2} \quad[\because k=\frac{1}{c}] \end{aligned} $
Hence, the required solution is $y=k x e^{-x^{2} / 2}$.
9. Solve the differential equation $\frac{d y}{d x}=1+x+y^{2}+x y^{2}$, when $y=0, x=0$.
Show Answer
Solution
Given equation is
$ \begin{aligned} \frac{d y}{d x} & =1+x+y^{2}+x y^{2} \\ \Rightarrow \quad \frac{d y}{d x} & =1(1+x)+y^{2}(1+x) \\ \Rightarrow \quad \frac{d y}{d x} & =(1+x)(1+y^{2}) \Rightarrow \frac{d y}{1+y^{2}}=(1+x) d x \end{aligned} $
Integrating both sides, we get
$ \int \frac{d y}{1+y^{2}}=\int(1+x) d x \Rightarrow \tan ^{-1} y=x+\frac{x^{2}}{2}+c $
Put $x=0$ and $y=0$, we get $\tan ^{-1}(0)=0+0+c \Rightarrow c=0$
$\therefore \quad \tan ^{-1} y=x+\frac{x^{2}}{2} \Rightarrow y=\tan (x+\frac{x^{2}}{2})$
Hence, the required solution is $y=\tan (x+\frac{x^{2}}{2})$.
10. Find the general solution of $(x+2 y^{3}) \frac{d y}{d x}=y$.
Show Answer
Solution
Given equation is $(x+2 y^{3}) \frac{d y}{d x}=y$
$ \begin{aligned} & \Rightarrow \quad \frac{d y}{d x}=\frac{y}{x+2 y^{3}} \Rightarrow \frac{d x}{d y}=\frac{x+2 y^{3}}{y} \\ & \Rightarrow \quad \frac{d x}{d y}=\frac{x}{y}+\frac{2 y^{3}}{y} \Rightarrow \frac{d x}{d y}-\frac{x}{y}=2 y^{2} \end{aligned} $
Here $P=-\frac{1}{y}$ and $Q=2 y^{2}$.
$\therefore$ Integrating factor I.F. $=e^{\int P d y}=e^{\int-\frac{1}{y} d y}=e^{-\log y}=e^{\log \frac{1}{y}}=\frac{1}{y}$.
So the solution of the equation is
$ \begin{aligned} x . I . F . & =\int \text{ Q.I.F. } d y+c \\ x \cdot \frac{1}{y} & =\int 2 y^{2} \cdot \frac{1}{y} d y+c \\ \Rightarrow \quad \frac{x}{y} & =2 \int y d y+c \Rightarrow \frac{x}{y}=2 \cdot \frac{y^{2}}{2}+c \Rightarrow \frac{x}{y}=y^{2}+c \end{aligned} $
So $x=y^{3}+c y=y(y^{2}+c)$
Hence, the required solution is $x=y(y^{2}+c)$.
11. If $y(x)$ is a solution of $(\frac{2+\sin x}{1+y}) \frac{d y}{d x}=-\cos x$ and $y(0)=1$, then find the value of $y(\frac{\pi}{2})$.
Show Answer
Solution
Given equation is
$ \begin{aligned} & (\frac{2+\sin x}{1+y}) \frac{d y}{d x}=-\cos x \\ \Rightarrow & (\frac{2+\sin x}{\cos x}) \frac{d y}{d x}=-(1+y) \Rightarrow \frac{d y}{(1+y)}=-(\frac{\cos x}{2+\sin x}) d x \end{aligned} $
Integrating both sides, we get
$ \begin{aligned} \int \frac{d y}{1+y} & =-\int \frac{\cos x}{2+\sin x} d x \\ \log |1+y| & =-\log |2+\sin x|+\log c \\ \Rightarrow \log |1+y|+\log |2+\sin x| & =\log c \\ \Rightarrow \quad \log (1+y)(2+\sin x) & =\log c \Rightarrow(1+y)(2+\sin x)=c \end{aligned} $
Put $x=0$ and $y=1$, we get
$(1+1)(2+\sin 0)=c \Rightarrow 4=c$
$\therefore$ equation is $(1+y)(2+\sin x)=4$
Now put $x=\frac{\pi}{2}$
$ \begin{aligned} & \therefore \quad(1+y)(2+\sin \frac{\pi}{2})=4 \\ & \Rightarrow \quad(1+y)(2+1)=4 \Rightarrow 1+y=\frac{4}{3} \Rightarrow y=\frac{4}{3}-1 \Rightarrow \frac{1}{3} \end{aligned} $
So, $y(\frac{\pi}{2})=\frac{1}{3}$
Hence, the required solution is $y(\frac{\pi}{2})=\frac{1}{3}$.
12. If $y(t)$ is a solution of $(1+t) \frac{d y}{d t}-t y=1$ and $y(0)=-1$, then show that $y(1)=-\frac{1}{2}$.
Show Answer
Solution
Given equation is
$ (1+t) \frac{d y}{d t}-t y=1 \Rightarrow \frac{d y}{d t}-(\frac{t}{1+t}) y=\frac{1}{1+t} $
Here, $P=\frac{-t}{1+t}$ and $Q=\frac{1}{1+t}$
$\therefore$ Integrating factor I.F. $=e^{\int P d t}=e^{\int \frac{-t}{1+t} d t}=e^{-\int \frac{1+t-1}{1+t} d t}$
$\therefore$ I.F. $=e^{-t} \cdot(1+t)$
$ \begin{aligned} & =e^{-\int(1-\frac{1}{1+t}) d t}=e^{-[t-\log (1+t)]} \\ & =e^{-t+\log (1+t)}=e^{-t} \cdot e^{\log (1+t)} \end{aligned} $
Required solution of the given differential equation is
$ \begin{matrix} y \cdot \text{ I.F. } =\int \text{ Q.I.F. } d t+c \\ \Rightarrow \qquad y \cdot e^{-t}(1+t) =\int \frac{1}{(1+t)} \cdot e^{-t} \cdot(1+t) d t+c \\ \Rightarrow \qquad y \cdot e^{-t}(1+t) =\int e^{-t} d t+c \\ \Rightarrow \qquad y \cdot e^{-t}(1+t) =-e^{-t}+c \end{matrix} $
$ \begin{aligned} & \text{ Put } t=0 \text{ and } y=-1 \\ & \Rightarrow \quad-1 \cdot e^{0} \cdot 1=-e^{0}+c \\ & \Rightarrow \quad-1=-1+c \Rightarrow c=0 \end{aligned} $
So the equation becomes
Now put $t=1$
$ y e^{-t}(1+t)=-e^{-t} $
$\therefore \quad y \cdot e^{-1}(1+1)=-e^{-1}$
$\Rightarrow \quad 2 y=-1 \Rightarrow y=-\frac{1}{2}$
Hence $y(1)=-\frac{1}{2}$ is verified.
$[\because y(0)=-1]$
13. Form the differential equation having $y=(\sin ^{-1} x)^{2}+A$ $\cos ^{-1} x+B$ where $A$ and $B$ are arbitrary constants, as its general solution.
Show Answer
Solution
Given equation is $y=(\sin ^{-1} x)^{2}+A \cos ^{-1} x+B$
$ \frac{d y}{d x}=2 \sin ^{-1} x \cdot \frac{1}{\sqrt{1-x^{2}}}+A \cdot(\frac{-1}{\sqrt{1-x^{2}}}) $
Multiplying both sides by $\sqrt{1-x^{2}}$, we get
$ \sqrt{1-x^{2}} \frac{d y}{d x}=2 \sin ^{-1} x-A $
Again differentiating w.r.t $x$, we get
$ \begin{aligned} & \sqrt{1-x^{2}} \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x} \cdot \frac{1 \times(-2 x)}{2 \sqrt{1-x^{2}}}=\frac{2}{\sqrt{1-x^{2}}} \\ \Rightarrow \quad & \sqrt{1-x^{2}} \frac{d^{2} y}{d x^{2}}-\frac{x}{\sqrt{1-x^{2}}} \frac{d y}{d x}=\frac{2}{\sqrt{1-x^{2}}} \end{aligned} $
Multiplying both sides by $\sqrt{1-x^{2}}$, we get
$ \Rightarrow \quad(1-x^{2}) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}-2=0 $
Which is the required differential equation.
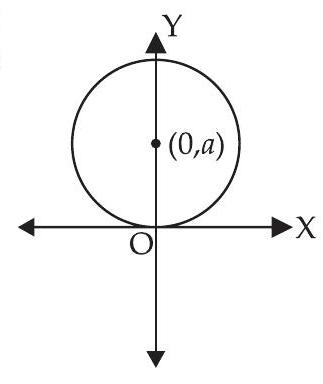
14. Form the differential equation of all circles which pass through origin and whose centres lie on $y$-axis.
Show Answer
Solution
Equation of circle which passes through the origin and whose centre lies on $y$-axis is
$$(x-0)^{2}+(y-a)^{2} =a^{2}$$
$$\Rightarrow \qquad x^{2}+y^{2}+a^{2}-2 a y =a^{2}$$
$$\Rightarrow \qquad x^{2}+y^{2}-2 a y =0 \tag{i}$$
$\Rightarrow \quad 2 x+2 y \cdot \frac{d y}{d x}-2 a \cdot \frac{d y}{d x}=0$
$\Rightarrow \quad x+y \frac{d y}{d x}-a \cdot \frac{d y}{d x}=0 \Rightarrow x+(y-a) \cdot \frac{d y}{d x}=0$
$ y-a=\frac{x}{d y / d x} $
$ \therefore \quad a=y+\frac{-x}{d y / d x} $
Putting the value of $a$ in eq. (i), we get
$ \begin{aligned} & x^{2}+y^{2}-2(y+\frac{x}{d y / d x}) y=0 \\ & \Rightarrow \quad x^{2}+y^{2}-2 y^{2}-\frac{2 x y}{\frac{d y}{d x}}=0 \Rightarrow x^{2}-y^{2}=\frac{2 x y}{\frac{d y}{d x}} \\ & \therefore \quad(x^{2}-y^{2}) \frac{d y}{d x}-2 x y=0 \end{aligned} $
Hence, the required differential equation is
$ (x^{2}-y^{2}) \frac{d y}{d x}-2 x y=0 $
15. Find the equation of a curve passing through origin and satisfying the differential equation $(1+x^{2}) \frac{d y}{d x}+2 x y=4 x^{2}$.
Show Answer
Solution
Given equation is
$ \begin{aligned} & (1+x^{2}) \frac{d y}{d x}+2 x y=4 x^{2} \\ & \Rightarrow \quad \frac{d y}{d x}+\frac{2 x}{1+x^{2}} \cdot y=\frac{4 x^{2}}{1+x^{2}} \end{aligned} $
Here, $P=\frac{2 x}{1+x^{2}}$ and $Q=\frac{4 x^{2}}{1+x^{2}}$
Integrating factor I.F. $=e^{\int P d x}=e^{\int \frac{2 x}{1+x^{2}} d x}=e^{\log (1+x^{2})}=1+x^{2}$
$\therefore$ Solution is
$$ \begin{align*} & y \times \text{ I.F. }=\int Q \times \text{ I.F. } d x+c \\ & \Rightarrow y(1+x^{2})=\int \frac{4 x^{2}}{1+x^{2}} \times(1+x^{2}) d x+c \\ & \Rightarrow \quad y(1+x^{2})=\int 4 x^{2} d x+c \\ & \Rightarrow \quad y(1+x^{2})=\frac{4}{3} x^{3}+c \tag{i} \end{align*} $$
Since the curve is passing through origin i.e., $(0,0)$
$\therefore$ Put $y=0$ and $x=0$ in eq. (i)
$0(1+0)=\frac{4}{3}(0)^{3}+c \Rightarrow c=0$
$\therefore$ Equation is $y(1+x^{2})=\frac{4}{3} x^{3} \Rightarrow y=\frac{4 x^{3}}{3(1+x^{2})}$
Hence, the required solution is $y=\frac{4 x^{3}}{3(1+x^{2})}$.
16. Solve : $x^{2} \cdot \frac{d y}{d x}=x^{2}+x y+y^{2}$
Show Answer
Solution
Given equation is $x^{2} \frac{d y}{d x}=x^{2}+x y+y^{2}$
$ \Rightarrow \quad \frac{d y}{d x}=\frac{x^{2}+x y+y^{2}}{x^{2}} $
Put $y=v x$
$\therefore \quad \frac{d y}{d x}=v+x \cdot \frac{d v}{d x}$
differential equation]
$\therefore \quad v+x \cdot \frac{d v}{d x}=\frac{x^{2}+v x^{2}+v^{2} x^{2}}{x^{2}}$
$\Rightarrow \quad v+x \cdot \frac{d v}{d x}=\frac{x^{2}(1+v+v^{2})}{x^{2}}$
$\Rightarrow \quad v+x \cdot \frac{d v}{d x}=1+v+v^{2} \Rightarrow x \cdot \frac{d v}{d x}=1+v+v^{2}-v$
$ \Rightarrow \quad x \cdot \frac{d v}{d x}=1+v^{2} \Rightarrow \frac{d v}{1+v^{2}}=\frac{d x}{x} $
Integrating both sides, we get
$ \begin{aligned} \int \frac{d v}{1+v^{2}} & =\int \frac{d x}{x} \\ \Rightarrow \quad \tan ^{-1} v & =\log x+c \Rightarrow \tan ^{-1}(\frac{y}{x})=\log x+c \end{aligned} $
Hence, the required solution is $\tan ^{-1}(\frac{y}{x})=\log |x|+c$.
17. Find the general solution of the differential equation
$ (1+y^{2})+(x-e^{\tan ^{-1} y}) \frac{d y}{d x}=0 $
Show Answer
Solution
Given equation is
$ \begin{aligned} & (1+y^{2})+(x-e^{\tan ^{-1} y}) \frac{d y}{d x}=0 \\ \Rightarrow & (x-e^{\tan ^{-1} y}) \frac{d y}{d x}=-(1+y^{2}) \Rightarrow \frac{d y}{d x}=\frac{-(1+y^{2})}{x-e^{\tan ^{-1} y}} \\ \Rightarrow & \quad \frac{d x}{d y}=\frac{x-e^{\tan ^{-1} y}}{-(1+y^{2})} \Rightarrow \frac{d x}{d y}=-\frac{x}{(1+y^{2})}+\frac{e^{\tan ^{-1} y}}{1+y^{2}} \\ \Rightarrow & \frac{d x}{d y}+\frac{x}{(1+y^{2})}=\frac{e^{\tan ^{-1} y}}{1+y^{2}} \end{aligned} $
Here, $P=\frac{1}{1+y^{2}}$ and $Q=\frac{e^{\tan ^{-1} y}}{1+y^{2}}$
$\therefore$ Integrating factor I.F. $=e^{\int P d y}=e^{\int \frac{1}{1+y^{2}} d y}=e^{\tan ^{-1} y}$
$\therefore$ Solution is
$ \begin{aligned} x . \text{ I.F. } & =\int \text{ Q.I.F. } d y+c \\ \Rightarrow \quad x \cdot e^{\tan ^{-1} y} & =\int \frac{e^{\tan ^{-1} y}}{1+y^{2}} \cdot e^{\tan ^{-1} y} d y+c \end{aligned} $
Put $e^{\tan ^{-1} y}=t$
$\therefore e^{\tan ^{-1} y} \cdot \frac{1}{1+y^{2}} d y=d t$
$\therefore \quad x \cdot e^{\tan ^{-1} y}=\int t \cdot d t+c$
$\Rightarrow x \cdot e^{\tan ^{-1} y}=\frac{1}{2} t^{2}+c$
$ \begin{aligned} & \Rightarrow \quad x \cdot e^{\tan ^{-1} y}=\frac{1}{2}(e^{\tan ^{-1} y})^{2}+c \Rightarrow x=\frac{1}{2}(e^{\tan ^{-1} y})+\frac{c}{e^{\tan ^{-1} y}} \\ & \Rightarrow \quad 2 x=e^{\tan ^{-1} y}+\frac{2 c}{e^{\tan ^{-1} y}} \\ & \Rightarrow 2 x \cdot e^{\tan ^{-1} y}=(e^{\tan ^{-1} y})^{2}+2 c \end{aligned} $
Hence, this is the required general solution.
18. Find the general solution of $y^{2} d x+(x^{2}-x y+y^{2}) d y=0$.
Show Answer
Solution
The given equation is $y^{2} d x+(x^{2}-x y+y^{2}) d y=0$.
$ \begin{matrix} \Rightarrow & y^{2} d x=-(x^{2}-x y+y^{2}) d y \\ \Rightarrow & \frac{d x}{d y}=-\frac{x^{2}-x y+y^{2}}{y^{2}} \end{matrix} $
Since it is a homogeneous differential equation
$\therefore$ Put $x=v y \Rightarrow \frac{d x}{d y}=v+y \cdot \frac{d v}{d y}$
So, $\quad v+y \cdot \frac{d v}{d y}=-(\frac{v^{2} y^{2}-v y^{2}+y^{2}}{y^{2}})$
$\Rightarrow \quad v+y \cdot \frac{d v}{d y}=-\frac{y^{2}(v^{2}-v+1)}{y^{2}}$
$\Rightarrow \quad v+y \cdot \frac{d v}{d y}=(-v^{2}+v-1) \Rightarrow y \cdot \frac{d v}{d y}=-v^{2}+v-1-v$
$\Rightarrow \quad y \cdot \frac{d v}{d y}=-v^{2}-1 \Rightarrow \frac{d v}{(v^{2}+1)}=-\frac{d y}{y}$
Integrating both sides, we get
$ \begin{aligned} & \Rightarrow \quad \int \frac{d v}{(v^{2}+1)}=-\int \frac{d y}{y} \Rightarrow \tan ^{-1} v=-\log y+c \\ & \Rightarrow \quad \tan ^{-1}(\frac{x}{y})+\log y+c \end{aligned} $
Hence the required solution is $\tan ^{-1}(\frac{x}{y})+\log y=c$.
19. Solve: $(x+y)(d x-d y)=d x+d y$.
Show Answer
Solution
Given differential equation is
$\qquad (x+y)(d x-d y) =d x+d y$
$\Rightarrow \quad (x+y) d x-(x+y) d y =d x+d y$
$\Rightarrow \quad -(x+y) d y-d y =d x-(x+y) d x$
$ \begin{aligned} \Rightarrow \quad -(x+y+1) d y =-(x+y-1) d x \\ \Rightarrow \frac{d y}{d x} =\frac{x+y-1}{x+y+1} \end{aligned} $
Put $x+y=z$
$ \begin{aligned} \therefore \quad 1+\frac{d y}{d x} & =\frac{d z}{d x} \\ \frac{d y}{d x} & =\frac{d z}{d x}-1 \end{aligned} $
So, $\quad \frac{d z}{d x}-1=\frac{z-1}{z+1}$
$\Rightarrow \quad \frac{d z}{d x}=\frac{z-1}{z+1}+1 \Rightarrow \frac{d z}{d x}=\frac{z-1+z+1}{z+1}$
$\Rightarrow \quad \frac{d z}{d x}=\frac{2 z}{z+1} \quad \Rightarrow \frac{z+1}{z} d z=2 \cdot d x$
Integrating both sides, we get
$ \begin{aligned} & \int \frac{z+1}{z} d z=2 \int d x \\ & \Rightarrow \quad \int(1+\frac{1}{z}) d z=2 \int d x \\ & \Rightarrow \quad z+\log |z|=2 x+\log |c| \\ & \Rightarrow \quad x+y+\log |x+y|=2 x+\log |c| \\ & \Rightarrow \quad y+\log |x+y|=x+\log |c| \\ & \Rightarrow \quad \log |x+y|=x-y+\log |c| \\ & \Rightarrow \log |x+y|-\log |c|=(x-y) \\ & \Rightarrow \quad \log |\frac{x+y}{c}|=(x-y) \Rightarrow \frac{x+y}{c}=e^{x-y} \\ & \therefore \quad x+y=c \cdot e^{x-y} \end{aligned} $
Hence, the required solution is $x+y=c \cdot e^{x-y}$.
20. Solve: $2(y+3)-x y \cdot \frac{d y}{d x}=0$, given that $y(1)=-2$.
Show Answer
Solution
Given differential equation is
$ \begin{aligned} 2(y+3)-x y \cdot \frac{d y}{d x} & =0 \\ \Rightarrow \quad x y \cdot \frac{d y}{d x} & =2 y+6 \\ \Rightarrow \quad(\frac{y}{2 y+6}) d y & =\frac{d x}{x} \Rightarrow \frac{1}{2}(\frac{y}{y+3}) d y=\frac{d x}{x} \end{aligned} $
Integrating both sides, we get
$ \begin{aligned} & \Rightarrow \quad \frac{1}{2} \int \frac{y}{y+3} \cdot d y=\int \frac{d x}{x} \Rightarrow \frac{1}{2} \int \frac{y+3-3}{y+3} d y=\int \frac{d x}{x} \\ & \Rightarrow \quad \frac{1}{2} \int(1-\frac{3}{y+3}) d y=\int \frac{d x}{x} \end{aligned} $
$ \begin{aligned} & \Rightarrow \frac{1}{2} \int 1 \cdot d y-\frac{3}{2} \int \frac{1}{y+3} d y=\int \frac{d x}{x} \\ & \Rightarrow \quad \frac{1}{2} y-\frac{3}{2} \log |y+3|=\log x+c \end{aligned} $
Put $x=1, y=-2$
$\Rightarrow \quad \frac{1}{2}(-2)-\frac{3}{2} \log |-2+3|=\log (1)+c$
$\Rightarrow \quad-1-\frac{3}{2} \log (1)=\log (1)+c$
$\Rightarrow \quad-1-0=0+c \qquad[\because \log (1)=0]$
$\therefore \quad c=-1$
$\therefore$ equation is
$\quad \frac{1}{2} y-\frac{3}{2} \log |y+3| =\log x-1$
$\Rightarrow \quad y-3 \log |y+3| =2 \log x-2$
$\Rightarrow \quad y-\log |(y+3)^{3}| =\log x^{2}-2$
$\Rightarrow \quad \log |(y+3)^{3}|+\log x^{2} =y+2$
$\Rightarrow \quad \log |x^{2}(y+3)^{3}|=y+2\Rightarrow x^{2}(y+3)^{3}=e^{y+2}$
Hence, the required solution is $x^{2}(y+3)^{3}=e^{y+2}$.
21. Solve the differential equation $d y=\cos x(2-y \cosec x) d x$ given that $y=2$ when $x=\frac{\pi}{2}$.
Show Answer
Solution
The given differential equation is
$ d y=\cos x(2-y cosec x) d x $
$\Rightarrow \frac{d y}{d x}=\cos x(2-y cosec x) \Rightarrow \frac{d y}{d x}=2 \cos x-y \cos x \cdot cosec x$
$\Rightarrow \frac{d y}{d x}=2 \cos x-y \cot x \Rightarrow \frac{d y}{d x}+y \cot x=2 \cos x$
Here, $P=\cot x$ and $Q=2 \cos x$.
$\therefore$ Integrating factor I.F. $=e^{\int P d x}=e^{\int \cot x d x}=e^{\log \sin x}=\sin x$
$\therefore$ Required solution is $y \times$ I.F $=\int Q \times$ I.F. $d x+c$ $\Rightarrow y \cdot \sin x=\int 2 \cos x \cdot \sin x d x+c$
$\Rightarrow y \cdot \sin x=\int \sin 2 x d x+c \Rightarrow y \cdot \sin x=-\frac{1}{2} \cos 2 x+c$
Put $x=\frac{\pi}{2}$ and $y=2$, we get
$ \begin{aligned} 2 \sin \frac{\pi}{2} & =-\frac{1}{2} \cos \pi+c \\ \Rightarrow \quad 2(1) & =-\frac{1}{2}(-1)+c \Rightarrow 2=\frac{1}{2}+c \Rightarrow c=2-\frac{1}{2}=\frac{3}{2} \end{aligned} $
$\therefore$ The equation is $y \sin x=-\frac{1}{2} \cos 2 x+\frac{3}{2}$.
22. Form the differential equation by eliminating $A$ and $B$ in $A x^{2}+B y^{2}=1$.
Show Answer
Solution
Given that $A x^{2}+B y^{2}=1$
Differentiating w.r.t. $x$, we get
$\qquad 2 A \cdot x+2 B y \frac{d y}{d x} =0$
$\Rightarrow \qquad A x+B y \cdot \frac{d y}{d x} =0 \Rightarrow B y \cdot \frac{d y}{d x}=-A x$
$\therefore \qquad \frac{y}{x} \cdot \frac{d y}{d x} =-\frac{A}{B}$
Differentiating both sides again w.r.t. $x$, we have
$ \begin{aligned} & \frac{y}{x} \cdot \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}(\frac{x \cdot \frac{d y}{d x}-y \cdot 1}{x^{2}})=0 \\ \Rightarrow & \frac{y x^{2}}{x} \cdot \frac{d^{2} y}{d x^{2}}+x \cdot(\frac{d y}{d x})^{2}-y \cdot \frac{d y}{d x}=0 \\ \Rightarrow & x y \cdot \frac{d^{2} y}{d x^{2}}+x \cdot(\frac{d y}{d x})^{2}-y \cdot \frac{d y}{d x}=0 \Rightarrow x y \cdot y^{\prime \prime}+x \cdot(y^{\prime})^{2}-y \cdot y^{\prime}=0 \end{aligned} $
Hence, the required equation is
$ x y \cdot y^{\prime \prime}+x \cdot(y^{\prime})^{2}-y \cdot y^{\prime}=0 $
23. Solve the differential equation $(1+y^{2}) \tan ^{-1} x d x+2 y(1+x^{2}) d y=0$.
Show Answer
Solution
Given differential equation is
$ \begin{matrix} (1+y^{2}) \tan ^{-1} x d x+2 y(1+x^{2}) d y=0 \\ \Rightarrow \qquad 2 y(1+x^{2}) d y=-(1+y^{2}) \cdot \tan ^{-1} x \cdot d x \\ \Rightarrow \qquad \frac{2 y}{1+y^{2}} d y=-\frac{\tan ^{-1} x}{1+x^{2}} \cdot d x \end{matrix} $
Integrating both sides, we get
$\int \frac{2 y}{1+y^{2}} d y =-\int \frac{\tan ^{-1} x}{1+x^{2}} \cdot d x $
$\Rightarrow \quad \log |1+y^{2}| =-\frac{1}{2}(\tan ^{-1} x)^{2}+c$
$\Rightarrow \quad \frac{1}{2}(\tan ^{-1} x)^{2}+\log |1+y^{2}|=c$
Which is the required solution.
24. Find the differential equation of system of concentric circles with centre $(1,2)$.
Show Answer
Solution
Family of concentric circles with centre $(1,2)$ and radius ’ $r$ ’ is
$ (x-1)^{2}+(y-2)^{2}=r^{2} $
Differentiating both sides w.r.t., $x$ we get
$ 2(x-1)+2(y-2) \frac{d y}{d x}=0 \Rightarrow(x-1)+(y-2) \frac{d y}{d x}=0 $
Which is the required equation.
Long Answer Type Questions
25. Solve: $y+\frac{d}{d x}(x y)=x(\sin x+\log x)$
Show Answer
Solution
The given differential equation is
$ \begin{aligned} & y+\frac{d}{d x}(x y)=x(\sin x+\log x) \\ & \Rightarrow \quad y+x \cdot \frac{d y}{d x}+y=x(\sin x+\log x) \\ & \Rightarrow \quad x \frac{d y}{d x}=x(\sin x+\log x)-2 y \\ & \Rightarrow \quad \frac{d y}{d x}=(\sin x+\log x)-\frac{2 y}{x} \Rightarrow \frac{d y}{d x}+\frac{2}{x} y=(\sin x+\log x) \end{aligned} $
Here, $P=\frac{2}{x}$ and $Q=(\sin x+\log x)$
Integrating factor I.F. $=e^{\int P d x}=e^{\int \frac{2}{x} d x}=e^{2 \log x}=e^{\log x^{2}}=x^{2}$
$\therefore$ Solution is
$$ \begin{align*} y \times \text{ I.F. } & =\int \text{ Q.I.F. } d x+c \\ \Rightarrow \quad y \cdot x^{2} & =\int(\sin x+\log x) x^{2} d x+c \tag{1} \end{align*} $$
Let I
$ \begin{aligned} & =\int(\sin x+\log x) x^{2} d x \\ & =\int x_I^{2} \sin _{II} x d x+\int _{II} x^{2} \log x d x \\ & \begin{aligned} = & {[x^{2} \cdot \int \sin x d x-\int(D(x^{2}) \cdot \int \sin x d x) d x]+} \\ & {[\log x \cdot \int x^{2} d x-\int(D(\log x) \cdot \int x^{2} d x) d x] } \end{aligned} \\ & =[x^{2}(-\cos x)-2 \int-x \cos x d x]+[\log x \cdot \frac{x^{3}}{3}-\int \frac{1}{x} \cdot \frac{x^{3}}{3} d x] \\ & =[-x^{2} \cos x+2(x \sin x-\int 1 \cdot \sin x d x)]+[\frac{x^{3}}{3} \log x-\frac{1}{3} \int x^{2} d x] \\ & =-x^{2} \cos x+2 x \sin x+2 \cos x+\frac{x^{3}}{3} \log x-\frac{1}{9} x^{3} \end{aligned} $
Now from eq (1) we get,
$ \begin{aligned} y \cdot x^{2} & =-x^{2} \cos x+2 x \sin x+2 \cos x+\frac{x^{3}}{3} \log x-\frac{1}{9} x^{3}+c \\ \therefore \quad & y=-\cos x+\frac{2 \sin x}{x}+\frac{2 \cos x}{x^{2}}+\frac{x \log x}{3}-\frac{1}{9} x+c \cdot x^{-2} \end{aligned} $
Hence, the required solution is
$ y=-\cos x+\frac{2 \sin x}{x}+\frac{2 \cos x}{x^{2}}+\frac{x \log x}{3}-\frac{1}{9} x+c \cdot x^{-2} $
26. Find the general solution of $(1+\tan y)(d x-d y)+2 x d y=0$.
Show Answer
Solution
Given that: $(1+\tan y)(d x-d y)+2 x d y=0$
$\Rightarrow \quad(1+\tan y) d x-(1+\tan y) d y+2 x d y=0$
$ \Rightarrow \quad(1+\tan y) d x-(1+\tan y-2 x) d y=0 $
$ \begin{aligned} & \Rightarrow \quad(1+\tan y) \frac{d x}{d y}=(1+\tan y-2 x) \Rightarrow \frac{d x}{d y}=\frac{1+\tan y-2 x}{1+\tan y} \\ & \Rightarrow \quad \frac{d x}{d y}=1-\frac{2 x}{1+\tan y} \Rightarrow \frac{d x}{d y}+\frac{2 x}{1+\tan y}=1 \end{aligned} $
Here, $P=\frac{2}{1+\tan y}$ and $Q=1$
Integrating factor I.F.
$ \begin{aligned} & =e^{\int \frac{2}{1+\tan y} d y}=e^{\int \frac{2 \cos . y}{\sin y+\cos y} d y} \\ & =e^{\int \frac{\sin y+\cos y-\sin y+\cos y}{(\sin y+\cos y)} d y}=e^{\int(1+\frac{\cos y-\sin y}{\sin y+\cos y}) d y} \\ & =e^{\int 1 \cdot d y} \cdot e^{\int \frac{\cos y-\sin y}{\sin y+\cos y} d y} \\ & =e^{y} \cdot e^{\log (\sin y+\cos y)}=e^{y} \cdot(\sin y+\cos y) \end{aligned} $
So, the solution is $\quad x \times$ I.F. $=\int Q \times$ I.F. $d y+c$
$\Rightarrow x \cdot e^{y}(\sin y+\cos y)=\int 1 \cdot e^{y}(\sin y+\cos y) d y+c$
$\Rightarrow \quad x \cdot e^{y}(\sin y+\cos y)=e^{y} \cdot \sin y+c$
$ [\because \int e^{x}[f(x)+f^{\prime}(x)] d x=e^{x} f(x)+c] $
$\Rightarrow \quad x(\sin y+\cos y)=\sin y+c \cdot e^{-y}$
Hence, the required solution is $x(\sin y+\cos y)=\sin y+c \cdot e^{-y}$.
27. Solve : $\frac{d y}{d x}=\cos (x+y)+\sin (x+y)$. [Hint: Substitute $x+y=z$ ]
Show Answer
Solution
Given that : $\frac{d y}{d x}=\cos (x+y)+\sin (x+y)$
Put $\quad x+y=v$, on differentiating w.r.t. $x$, we get,
$1+\frac{d y}{d x} =\frac{d v}{d x}$
$\therefore \quad \frac{d y}{d x} =\frac{d v}{d x}-1$
$\therefore \quad \frac{d v}{d x}-1 =\cos v+\sin v$
$\Rightarrow \quad \frac{d v}{d x} =\cos v+\sin v+1$
$\Rightarrow \frac{d v}{\cos v+\sin v+1} =d x$
Integrating both sides, we have
$ \begin{aligned} \frac{d v}{\cos v+\sin v+1} =\int 1 . d x \\ \Rightarrow \quad \frac{d v}{(\frac{1-\tan ^{2} \frac{v}{2}}{1+\tan ^{2} \frac{v}{2}}+\frac{2 \tan \frac{v}{2}}{1+\tan ^{2} \frac{v}{2}}+1)} =\int 1 . d x \\ \Rightarrow \quad \int \frac{(1+\tan ^{2} \frac{v}{2})}{1-\tan ^{2} \frac{v}{2}+2 \tan \frac{v}{2}+1+\tan ^{2} \frac{v}{2}} d v =\int 1 . d x \\ \Rightarrow \quad \int \frac{\sec ^{2} \frac{v}{2}}{2+2 \tan ^{2}} d v =\int 1 . d x \\ \text{ Put } \quad 2+2 \tan \frac{v}{2} \end{aligned} $
$ \begin{matrix} 2 \cdot \frac{1}{2} \sec ^{2} \frac{v}{2} d v =d t \Rightarrow \sec ^{2} \frac{v}{2} d v=d t \\ \int \frac{d t}{t} =\int 1 \cdot d x \\ \Rightarrow \quad \log |t| =x+c \\ \Rightarrow \quad \log |2+2 \tan \frac{v}{2}| =x+c \\ \Rightarrow \quad \log |2+2 \tan (\frac{x+y}{2})|=x+c \Rightarrow \log 2[1+\tan (\frac{x+y}{2})]=x+c \\ \Rightarrow \quad \log 2+\log [1+\tan (\frac{x+y}{2})] =x+c \\ \Rightarrow \quad \log [1+\tan (\frac{x+y}{2})] =x+c-\log 2 \end{matrix} $
Hence, the required solution is
$ \log [1+\tan (\frac{x+y}{2})]=x+K \quad[c-\log 2=K] $
28. Find the general solution of $\frac{d y}{d x}-3 y=\sin 2 x$.
Show Answer
Solution
Given equation is $\frac{d y}{d x}-3 y=\sin 2 x$.
Here, $P=-3$ and $Q=\sin 2 x$
$\therefore$ Integrating factor I.F. $=e^{\int P d x}=e^{\int-3 d x}=e^{-3 x}$
$\therefore$ Solution is
$ \begin{aligned} & y \times \text{ I.F. }=\int Q . \text{ I.F. } d x+c \\ & \Rightarrow \quad y \cdot e^{-3 x}=\int \sin 2 x \cdot e^{-3 x} d x+c \\ & \text{ Let } \quad I=\int \sin _{I} 2 x \cdot e_II^{-3 x} d x \\ & \Rightarrow \quad I=\sin 2 x \cdot \int e^{-3 x} d x-\int(D(\sin 2 x) \cdot \int e^{-3 x} d x) d x \\ & \Rightarrow \quad I=\sin 2 x \cdot \frac{e^{-3 x}}{-3}-\int 2 \cos 2 x \cdot \frac{e^{-3 x}}{-3} d x \\ & \Rightarrow \quad I=\frac{e^{-3 x}}{-3} \sin 2 x+\frac{2}{3} \iint_I^{\cos 2 x} \cdot e_II^{-3 x} d x \\ & \Rightarrow \quad I=\frac{e^{-3 x}}{-3} \sin 2 x+\frac{2}{3}[\cos 2 x \cdot \int e^{-3 x} d x-. \\ & .\int[D \cos 2 x \cdot \int e^{-3 x} d x] d x] \end{aligned} $
$ \begin{aligned} \Rightarrow \quad I & =\frac{e^{-3 x}}{-3} \sin 2 x+\frac{2}{3}[\cos 2 x \cdot \frac{e^{-3 x}}{-3}-. \\ & .2 \sin 2 x \cdot \frac{e^{-3 x}}{-3}] d x \\ \Rightarrow \quad I & =\frac{e^{-3 x}}{-3} \sin 2 x-\frac{2}{9} \cos 2 x \cdot e^{-3 x}-\frac{4}{9} \int \sin 2 x \cdot e^{-3 x} d x \\ \Rightarrow \quad & =\frac{e^{-3 x}}{-3} \sin 2 x-\frac{2}{9} e^{-3 x} \cos 2 x-\frac{4}{9} I \\ \Rightarrow \quad I+\frac{4}{9} I & =\frac{e^{-3 x}}{-3} \sin 2 x-\frac{2}{9} e^{-3 x} \cos 2 x \\ \Rightarrow \quad \frac{13 I}{9} & =-\frac{1}{9}[3 e^{-3 x} \sin 2 x+2 e^{-3 x} \cos 2 x] \\ \Rightarrow \quad I & =-\frac{1}{13} e^{-3 x}[3 \sin 2 x+2 \cos 2 x] \end{aligned} $
$\therefore$ The equation becomes
$ \begin{aligned} y \cdot e^{-3 x} & =-\frac{1}{13} e^{-3 x}[3 \sin 2 x+2 \cos 2 x]+c \\ \therefore \quad y & =-\frac{1}{13}[3 \sin 2 x+2 \cos 2 x]+c \cdot e^{3 x} \end{aligned} $
Hence, the required solution is
$ y=-[\frac{3 \sin 2 x+2 \cos 2 x}{13}]+c \cdot e^{3 x} $
29. Find the equation of a curve passing through $(2,1)$ if the slope of the tangent to the curve at any point $(x, y)$ is $\frac{x^{2}+y^{2}}{2 x y}$.
Show Answer
Solution
Given that the slope of tangent to a curve at $(x, y)$ is
$ \frac{d y}{d x}=\frac{x^{2}+y^{2}}{2 x y} $
It is a homogeneous differential equation
So, put $y=v x \Rightarrow \frac{d y}{d x}=v+x \cdot \frac{d v}{d x}$
$ v+x \cdot \frac{d v}{d x}=\frac{x^{2}+v^{2} x^{2}}{2 x \cdot v x} $
$ \begin{aligned} & \Rightarrow \quad v+x \cdot \frac{d v}{d x}=\frac{1+v^{2}}{2 v} \\ & \Rightarrow \quad x \cdot \frac{d v}{d x}=\frac{1+v^{2}}{2 v}-v \Rightarrow x \cdot \frac{d v}{d x}=\frac{1+v^{2}-2 v^{2}}{2 v} \\ & \Rightarrow \quad x \cdot \frac{d v}{d x}=\frac{1-v^{2}}{2 v} \Rightarrow \frac{2 v}{1-v^{2}} d v=\frac{d x}{x} \end{aligned} $
Integrating both sides, we get
$ \begin{gathered} \int \frac{2 v}{1-v^{2}} d v=\int \frac{d x}{x} \Rightarrow-\log |1-v^{2}|=\log x+\log c \\ \Rightarrow-\log |1-\frac{y^{2}}{x^{2}}|=\log x+\log c \Rightarrow-\log |\frac{x^{2}-y^{2}}{x^{2}}|=\log x+\log c \\ \Rightarrow \log |\frac{x^{2}}{x^{2}-y^{2}}|=\log |x c| \Rightarrow \frac{x^{2}}{x^{2}-y^{2}}=x c \end{gathered} $
Since, the curve is passing through the point $(2,1)$
$ \therefore \quad \frac{(2)^{2}}{(2)^{2}-(1)^{2}}=2 c \Rightarrow \frac{4}{3}=2 c \Rightarrow c=\frac{2}{3} $
Hence, the required equation is
$ \frac{x^{2}}{x^{2}-y^{2}}=\frac{2}{3} x \Rightarrow 2(x^{2}-y^{2})=3 x $
30. Find the equation of the curve through the point $(1,0)$ if the slope of the tangent to the curve at any point $(x, y)$ is $\frac{y-1}{x^{2}+x}$.
Show Answer
Solution
Given that the slope of the tangent to the curve at $(x, y)$ is
$ \frac{d y}{d x}=\frac{y-1}{x^{2}+x} \Rightarrow \frac{d y}{y-1}=\frac{d x}{x^{2}+x} $
Integrating both sides, we have
$ \begin{aligned} & \int \frac{d y}{y-1}=\int \frac{d x}{x^{2}+x} \\ & \Rightarrow \quad \int \frac{d y}{y-1}=\int \frac{d x}{x^{2}+x+\frac{1}{4}-\frac{1}{4}} \text{ [making perfect square] } \\ & \Rightarrow \quad \int \frac{d y}{y-1}=\int \frac{d x}{(x+\frac{1}{2})^{2}-(\frac{1}{2})^{2}} \end{aligned} $
$ \begin{matrix} \Rightarrow & \log |y-1|=\frac{1}{2 \times \frac{1}{2}} \log |\frac{x+\frac{1}{2}-\frac{1}{2}}{x+\frac{1}{2}+\frac{1}{2}}|+\log c \\ \Rightarrow & \log |y-1|=\log |\frac{x}{x+1}|+\log c \\ \Rightarrow & \log |y-1|=\log |c(\frac{x}{x+1})| \\ \therefore & y-1=\frac{c x}{x+1} \Rightarrow(y-1)(x+1)=c x \end{matrix} $
Since, the line is passing through the point $(1,0)$, then $(0-1)(1+1)=c(1) \Rightarrow c=2$.
Hence, the required solution is $(y-1)(x+1)=2 x$.
31. Find the equation of a curve passing through origin if the slope of the tangent to the curve at any point $(x, y)$ is equal to the square of the difference of the abscissa and ordinate of the point.
Show Answer
Solution
Here, slope of the tangent of the curve $=\frac{d y}{d x}$ and the difference between the abscissa and ordinate $=x-y$.
$\therefore$ As per the condition, $\frac{d y}{d x}=(x-y)^{2}$
Put $x-y=v$
$ \begin{aligned} & 1-\frac{d y}{d x}=\frac{d v}{d x} \\ & \therefore \quad \frac{d y}{d x}=1-\frac{d v}{d x} \end{aligned} $
$\therefore$ the equation becomes
$ 1-\frac{d v}{d x}=v^{2} \Rightarrow \frac{d v}{d x}=1-v^{2} \Rightarrow \frac{d v}{1-v^{2}}=d x $
Integrating both sides, we get
$$ \begin{align*} \int \frac{d v}{1-v^{2}} & =\int d x \\ \Rightarrow \quad \frac{1}{2} \log |\frac{1+v}{1-v}| & =x+c \quad \Rightarrow \quad \frac{1}{2} \log |\frac{1+x-y}{1-x+y}|=x+c \tag{1} \end{align*} $$
Since, the curve is passing through $(0,0)$
then $\frac{1}{2} \log |\frac{1+0-0}{1-0+0}|=0+c \quad \Rightarrow \quad c=0$ $\therefore$ On putting $c=0$ in eq. (1) we get
$ \begin{aligned} & & \frac{1}{2} \log |\frac{1+x-y}{1-x+y}| & =x \Rightarrow \log |\frac{1+x-y}{1-x+y}| \\ & \therefore & \frac{1+x-y}{1-x+y} & =e^{2 x} \\ \Rightarrow & & (1+x-y) & =e^{2 x}(1-x+y) \end{aligned} $
Hence, the required equation is $(1+x-y)=e^{2 x}(1-x+y)$.
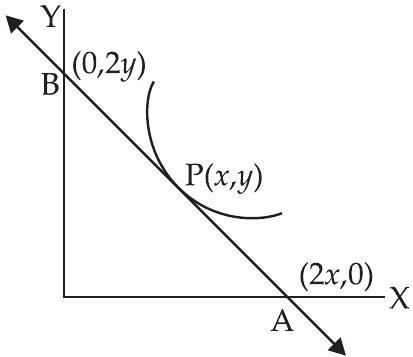
32. Find the equation of a curve passing through the point $(1,1)$, if the tangent drawn at any point $P(x, y)$ on the curve meets the coordinate axes at $A$ and $B$ such that $P$ is the mid point of $AB$.
Show Answer
Solution
Let $P(x, y)$ be any point on the curve and $AB$ be the tangent to the given curve at $P$.
$P$ is the mid point of $A B$ (given)
$\therefore$ Coordinates of $A$ and $B$ are $(2 x, 0)$ and $(0,2 y)$ respectively.
$\therefore$ Slope of the tangent
$ AB= $
$ \begin{aligned} & \frac{2 y-0}{0-2 x}=-\frac{y}{x} \\ & \therefore \quad \frac{d y}{d x}=-\frac{y}{x} \Rightarrow \frac{d y}{y}=-\frac{d x}{x} \end{aligned} $
Integrating both sides, we get
$ \begin{aligned} & \int \frac{d y}{y}=-\int \frac{d x}{x} \Rightarrow \log y=-\log x+\log c \\ & \Rightarrow \quad \log y+\log x=\log c \quad \Rightarrow \log y x=\log c \\ & \therefore \quad y x=c \end{aligned} $
Since, the curve passes through $(1,1)$
$ \begin{aligned} \therefore & & 1 \times 1 & =c \quad \therefore \quad c=1 \\ \Rightarrow & & y x & =1 \end{aligned} $
Hence, the required equation is $x y=1$.
33. Solve: $x \frac{d y}{d x}=y(\log y-\log x+1)$
Show Answer
Solution
Given that: $x \frac{d y}{d x}=y(\log y-\log x+1)$
$ \Rightarrow \quad x \frac{d y}{d x}=y[\log (\frac{y}{x})+1] \Rightarrow \frac{d y}{d x}=\frac{y}{x}[\log (\frac{y}{x})+1] $
Since, it is a homogeneous differential equation.
$\therefore$ Put $y=v x \Rightarrow \frac{d y}{d x}=v+x \cdot \frac{d v}{d x}$
$\therefore \quad v+x \cdot \frac{d v}{d x}=\frac{v x}{x}[\log (\frac{v x}{x})+1]$
$\Rightarrow \quad v+x \cdot \frac{d v}{d x}=v[\log v+1]$
$\Rightarrow \quad x \cdot \frac{d v}{d x}=v[\log v+1]-v \Rightarrow x \cdot \frac{d v}{d x}=v[\log v+1-1]$
$\Rightarrow \quad x \cdot \frac{d v}{d x}=v \cdot \log v \Rightarrow \frac{d v}{v \log v}=\frac{d x}{x}$
Integrating both sides, we get
Put $\log v=t$ on L.H.S.
$ \qquad \int \frac{d v}{v \log v}=\int \frac{d x}{x} $
$ \begin{matrix} \frac{1}{v} d v =dt \\ \therefore \quad \int \frac{d t}{t} =\int \frac{d x}{x} \\ \log |t| =\log |x|+\log c \\ \Rightarrow \quad \log |\log v| =\log x c \Rightarrow \log v=x c \\ \Rightarrow \quad \log (\frac{y}{x}) =x c \end{matrix} $
Hence, the required solution is $\log (\frac{y}{x})=x c$.
Objective Type Questions
34. The degree of the differential equation
$ (\frac{d^{2} y}{d x^{2}})^{2}+(\frac{d y}{d x})^{2}=x \sin (\frac{d y}{d x}) \text{ is } $
(a) 1
(b) 2
(c) 3
(d) not defined
Show Answer
Solution
The degree of the given differential equation is not defined because the value of $\sin (\frac{d y}{d x})$ on expansion will be in increasing power of $(\frac{d y}{d x})$.
-
Option (a) 1: This is incorrect because the degree of a differential equation is defined as the highest power of the highest order derivative, provided the equation is polynomial in derivatives. In this case, the equation involves a trigonometric function of the derivative, making it non-polynomial.
-
Option (b) 2: This is incorrect because, although the highest power of the second-order derivative is 2, the presence of the trigonometric function $\sin (\frac{d y}{d x})$ means the equation is not polynomial in its derivatives, so the degree is not defined.
-
Option (c) 3: This is incorrect because the degree of a differential equation is not simply the highest power of any derivative term. The equation must be polynomial in its derivatives, and the presence of $\sin (\frac{d y}{d x})$ means it is not polynomial, so the degree is not defined.
35. The degree of the differential equation $[1+(\frac{d y}{d x})^{2}]^{3 / 2}=\frac{d^{2} y}{d x^{2}}$ is
(a) 4
(b) $\frac{3}{2}$
(c) not defined
(d) 2
Show Answer
Solution
The given differential equation is
$ [1+(\frac{d y}{d x})^{2}]^{3 / 2}=(\frac{d^{2} y}{d x^{2}}) $
Squaring both sides, we have
$ [1+(\frac{d y}{d x})^{2}]^{3}=(\frac{d^{2} y}{d x^{2}})^{2} $
So, the degree of the given differential equation is 2 .
Hence, the correct option is $(d)$.
-
Option (a) 4: This option is incorrect because the degree of the differential equation is determined by the highest power of the highest order derivative after the equation is made polynomial in derivatives. In this case, after squaring both sides, the highest power of the highest order derivative ((\frac{d^2 y}{d x^2})) is 2, not 4.
-
Option (b) (\frac{3}{2}): This option is incorrect because the degree of a differential equation must be a whole number. The degree is defined as the exponent of the highest order derivative when the equation is expressed in polynomial form. In this case, the degree is 2, not a fractional value like (\frac{3}{2}).
-
Option (c) not defined: This option is incorrect because the degree of the differential equation can be defined. After squaring both sides of the given equation, it becomes a polynomial equation in terms of the highest order derivative ((\frac{d^2 y}{d x^2})), and the degree is clearly 2.
36. The order and degree of the differential equation $\frac{d^{2} y}{d x^{2}}+(\frac{d y}{d x})^{\frac{1}{4}}+x^{\frac{1}{5}}=0$ respectively are
(a) 2 and not defined
(b) 2 and 2
(c) 2 and 3
(d) 3 and 3
Show Answer
Solution
Given differential equation is
$ \begin{aligned} & \frac{d^{2} y}{d x^{2}}+(\frac{d y}{d x})^{\frac{1}{4}}+x^{\frac{1}{5}}=0 \\ & \Rightarrow \quad \frac{d^{2} y}{d x^{2}}+(\frac{d y}{d x})^{\frac{1}{4}}=-x^{\frac{1}{5}} \end{aligned} $
Since the degree of $\frac{d y}{d x}$ is in fraction.
So, the degree of the differential equation is not defined as the order is 2.
Hence, the correct option is $(a)$.
-
Option (b): 2 and 2
- Incorrect because the degree of the differential equation is not defined. The term ((\frac{d y}{d x})^{\frac{1}{4}}) has a fractional exponent, which means the degree cannot be an integer.
-
Option (c): 2 and 3
- Incorrect because the degree of the differential equation is not defined. The term ((\frac{d y}{d x})^{\frac{1}{4}}) has a fractional exponent, which means the degree cannot be an integer.
-
Option (d): 3 and 3
- Incorrect because the order of the differential equation is 2, not 3. The highest derivative present is (\frac{d^{2} y}{d x^{2}}), which indicates the order is 2. Additionally, the degree is not defined due to the fractional exponent in ((\frac{d y}{d x})^{\frac{1}{4}}).
37. If $y=e^{-x}(A \cos x+B \sin x)$, then $y$ is a solution of
(a) $\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0$
(b) $\frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+2 y=0$
(c) $\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}+2 y=0$
(d) $\frac{d^{2} y}{d x^{2}}+2 y=0$
Show Answer
Solution
Given equation is $y=e^{-x}(A \cos x+B \sin x)$
Differentiating both sides, w.r.t. $x$, we get
$ \begin{aligned} & \frac{d y}{d x}=e^{-x}(-A \sin x+B \cos x)-e^{-x}(A \cos x+B \sin x) \\ & \frac{d y}{d x}=e^{-x}(-A \sin x+B \cos x)-y \end{aligned} $
Again differentiating w.r.t. $x$, we get
$ \begin{aligned} & \frac{d^{2} y}{d x^{2}}=e^{-x}(-A \cos x-B \sin x)-e^{-x}(-A \sin x+B \cos x)-\frac{d y}{d x} \\ \Rightarrow & \frac{d^{2} y}{d x^{2}}=-e^{-x}(A \cos x+B \sin x)-[\frac{d y}{d x}+y]-\frac{d y}{d x} \\ \Rightarrow & \frac{d^{2} y}{d x^{2}}=-y-\frac{d y}{d x}-y-\frac{d y}{d x} \\ \Rightarrow & \frac{d^{2} y}{d x^{2}}=-2 \frac{d y}{d x}-2 y \Rightarrow \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}+2 y=0 \end{aligned} $
Hence, the correct option is (c)
-
Option (a): $\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0$
- This option is incorrect because it does not account for the term involving ( y ). The correct differential equation derived from the given function includes a term ( +2y ), which is missing in this option.
-
Option (b): $\frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+2 y=0$
- This option is incorrect because the sign in front of the first derivative term ( \frac{d y}{d x} ) is negative. The correct differential equation has a positive sign in front of ( 2 \frac{d y}{d x} ).
-
Option (d): $\frac{d^{2} y}{d x^{2}}+2 y=0$
- This option is incorrect because it does not include the first derivative term ( \frac{d y}{d x} ). The correct differential equation includes a term ( +2 \frac{d y}{d x} ), which is missing in this option.
38. The differential equation for $y=A \cos \alpha x+B \sin \alpha x$, where $A$ and $B$ are arbitrary constants is:
(a) $\frac{d^{2} y}{d x^{2}}-\alpha^{2} y=0$
(b) $\frac{d^{2} y}{d x^{2}}+\alpha^{2} y=0$
(c) $\frac{d^{2} y}{d x^{2}}+\alpha y=0$
(d) $\frac{d^{2} y}{d x^{2}}-\alpha y=0$
Show Answer
Solution
Given equation is : $y=A \cos \alpha x+B \sin \alpha x$ Differentiating both sides w.r.t. $x$, we have
$ \begin{aligned} \frac{d y}{d x} & =-A \sin \alpha x \cdot \alpha+B \cos \alpha x \cdot \alpha \\ & =-A \alpha \sin \alpha x+B \alpha \cos \alpha x \end{aligned} $
Again differentiating w.r.t. $x$, we get
$ \begin{aligned} \frac{d^{2} y}{d x^{2}} & =-A \alpha^{2} \cos \alpha x-B \alpha^{2} \sin \alpha x \\ \Rightarrow \quad \frac{d^{2} y}{d x^{2}} & =-\alpha^{2}(A \cos \alpha x+B \sin \alpha x) \\ \Rightarrow \quad \frac{d^{2} y}{d x^{2}} & =-\alpha^{2} y \Rightarrow \frac{d^{2} y}{d x^{2}}+\alpha^{2} y=0 \end{aligned} $
Hence, the correct option is (b).
-
Option (a): The equation $\frac{d^{2} y}{d x^{2}}-\alpha^{2} y=0$ is incorrect because, as derived, the second derivative of $y$ with respect to $x$ is $-\alpha^{2} y$. Therefore, the correct form should have a positive $\alpha^{2} y$ term on the left-hand side when moved to the right-hand side, resulting in $\frac{d^{2} y}{d x^{2}}+\alpha^{2} y=0$.
-
Option (c): The equation $\frac{d^{2} y}{d x^{2}}+\alpha y=0$ is incorrect because the term involving $\alpha$ should be squared. The correct differential equation involves $\alpha^{2}$, not just $\alpha$, as shown in the derivation.
-
Option (d): The equation $\frac{d^{2} y}{d x^{2}}-\alpha y=0$ is incorrect because, similar to option (c), the term involving $\alpha$ should be squared. The correct differential equation involves $\alpha^{2}$, not just $\alpha$, as shown in the derivation.
39. Solution of differential equation $x d y-y d x=0$ represents:
(a) a rectangular hyperbola
(b) parabola whose vertex is at origin
(c) straight line passing through origin
(d) a circle whose centre is at origin.
Show Answer
Solution
The given differential equation is
$ x d y-y d x=0 $
$ \Rightarrow \quad \frac{d y}{d x}=\frac{y}{x} \Rightarrow \frac{d y}{y}=\frac{d x}{x} $
Integrating both sides, we get
$ \begin{aligned} & \qquad \int \frac{d y}{y}=\int \frac{d x}{x} \\ & \Rightarrow \quad \log y=\log x+\log c \Rightarrow \log y=\log x c \\ & \Rightarrow \quad y=x c \text{ which is a straight line passing } \\ & \text{ through the origin. } \\ & \text{ Hence, the correct answer is }(c) \end{aligned} $
-
(a) a rectangular hyperbola: A rectangular hyperbola is represented by an equation of the form (xy = k), where (k) is a constant. The given differential equation (x , dy - y , dx = 0) simplifies to (y = cx), which is a linear relationship and not a hyperbolic one.
-
(b) parabola whose vertex is at origin: A parabola with its vertex at the origin typically has an equation of the form (y^2 = 4ax) or (x^2 = 4ay). The given differential equation (x , dy - y , dx = 0) leads to (y = cx), which is a straight line and not a parabolic curve.
-
(d) a circle whose centre is at origin: A circle with its center at the origin is represented by an equation of the form (x^2 + y^2 = r^2), where (r) is the radius. The given differential equation (x , dy - y , dx = 0) results in (y = cx), which describes a straight line and not a circular shape.
40. Integrating factor of the differential equation $\cos x \cdot \frac{d y}{d x}+y \sin x=1$ is
(a) $\cos x$
(b) $\tan x$
(c) $\sec x$
(d) $\sin x$
Show Answer
Solution
The given differential equation is
$ \begin{aligned} \cos x \cdot \frac{d y}{d x}+y \sin x =1 \\ \Rightarrow \qquad \frac{d y}{d x}+\frac{\sin x}{\cos x} y =\frac{1}{\cos x} \Rightarrow \frac{d y}{d x}+\tan x y=\sec x \end{aligned} $
Here, $P=\tan x$ and $Q=\sec x$
$\therefore$ Integrating factor $=e^{\int P d x}=e^{\int \tan x d x}=e^{\log \sec x}=\sec x$
Hence, the correct option is (c).
-
Option (a) $\cos x$: This is incorrect because the integrating factor is derived from the exponential of the integral of the coefficient of ( y ) in the standard form of the differential equation. The coefficient of ( y ) is ( \tan x ), not ( \cos x ). Therefore, ( \cos x ) is not the correct integrating factor.
-
Option (b) $\tan x$: This is incorrect because the integrating factor is found by taking the exponential of the integral of ( \tan x ). The integral of ( \tan x ) is ( \log |\sec x| ), and the exponential of this is ( \sec x ), not ( \tan x ).
-
Option (d) $\sin x$: This is incorrect because the integrating factor must be derived from the coefficient of ( y ) in the differential equation, which is ( \tan x ). The integral of ( \tan x ) does not involve ( \sin x ) directly, and thus ( \sin x ) cannot be the integrating factor.
41. Solution of differential equation $\tan y \sec ^{2} x d x+\tan x \sec ^{2} y d y=0$ is
(a) $\tan x+\tan y=k$
(b) $\tan x-\tan y=k$
(c) $\frac{\tan x}{\tan y}=k$
(d) $\tan x \cdot \tan y=k$
Show Answer
Solution
The given differential equation is
$ \tan y \sec ^{2} x d x+\tan x \sec ^{2} y d y=0 $
$\Rightarrow \tan x \sec ^{2} y d y=-\tan y \sec ^{2} x d x$
$\Rightarrow \quad \frac{\sec ^{2} y}{\tan y} \cdot d y=\frac{-\sec ^{2} x}{\tan x} \cdot d x$
Integrating both sides, we get
$ \begin{aligned} & \Rightarrow \quad \int \frac{\sec ^{2} y}{\tan y} d y=\int \frac{-\sec ^{2} x}{\tan x} d x \\ & \Rightarrow \quad \log |\tan y|=-\log |\tan x|+\log c \\ & \Rightarrow \quad \log |\tan y|+\log |\tan x|=\log c \end{aligned} $
-
Option (a) $\tan x + \tan y = k$: This option suggests a linear relationship between $\tan x$ and $\tan y$. However, the integration of the given differential equation results in a logarithmic relationship involving the product of $\tan x$ and $\tan y$, not their sum. Therefore, this option does not satisfy the derived solution.
-
Option (b) $\tan x - \tan y = k$: This option suggests a linear relationship involving the difference between $\tan x$ and $\tan y$. Similar to option (a), the integration of the given differential equation results in a logarithmic relationship involving the product of $\tan x$ and $\tan y$, not their difference. Hence, this option is also incorrect.
-
Option (c) $\frac{\tan x}{\tan y} = k$: This option suggests a ratio relationship between $\tan x$ and $\tan y$. The derived solution from the differential equation involves the product of $\tan x$ and $\tan y$, not their ratio. Therefore, this option does not match the solution obtained from the integration process.
42. Family $y=A x+A^{3}$ of curves is represented by the differential equation of degree
(a) 1
(b) 2
(c) 3
(d) 4
Show Answer
Solution
Given equation is $y=A x+A^{3}$
Differentiating both sides, we get
$ \frac{d y}{d x}=\text{ A which has degree } 1 \text{. } $
Hence, the correct answer is (a).
-
Option (b) is incorrect because the differential equation derived from the given family of curves, (\frac{dy}{dx} = A), is a first-order differential equation, not a second-order one.
-
Option (c) is incorrect because the differential equation derived from the given family of curves, (\frac{dy}{dx} = A), is a first-order differential equation, not a third-order one.
-
Option (d) is incorrect because the differential equation derived from the given family of curves, (\frac{dy}{dx} = A), is a first-order differential equation, not a fourth-order one.
43. Integrating factor of $x \frac{d y}{d x}-y=x-x$ is
(a) $x_1$
(c) $\frac{1}{x}$
(b) $\log x$
(d) $-x$
Show Answer
Solution
The given differential equation is
$ x \frac{d y}{d x}-y=x^{4}-3 x \Rightarrow \frac{d y}{d x}-\frac{y}{x}=x^{3}-3 $
Here, $P=-\frac{1}{x}$ and $Q=x^{3}-3$
So, integrating factor $=e^{\int P d x}=e^{\int-\frac{1}{x} d x}=e^{-\log x}=e^{\log \frac{1}{x}}=\frac{1}{x}$
Hence, the correct option is (c).
-
Option (a) $x_1$: This option is not a valid mathematical expression for an integrating factor. The notation $x_1$ is ambiguous and does not correspond to any standard form of an integrating factor.
-
Option (b) $\log x$: The integrating factor is derived from the exponential of the integral of $P$. In this case, $P = -\frac{1}{x}$, so the integrating factor should be $e^{\int -\frac{1}{x} dx} = e^{-\log x} = \frac{1}{x}$. $\log x$ does not fit this form and is not the correct integrating factor.
-
Option (d) $-x$: The integrating factor is derived from the exponential of the integral of $P$. Here, $P = -\frac{1}{x}$, so the integrating factor should be $e^{\int -\frac{1}{x} dx} = e^{-\log x} = \frac{1}{x}$. $-x$ does not match this form and is not the correct integrating factor.
44. Solution of $\frac{d y}{d x}-y=1, y(0)=1$ is given by
(a) $x y=-e^{x}$
(b) $x y=-e^{-x}$
(c) $x y=-1$
(d) $y=2 e^{x}-1$
Show Answer
Solution
The given differential equation is
$ \frac{d y}{d x}-y=1 $
Here, $P=-1, Q=1$
$\therefore$ Integrating factor, I.F. $=e^{\int P d x}=e^{\int-1 d x}=e^{-x}$
So, the solution is
$ \begin{aligned} & y \times \text{ I.F. }=\int \text{ Q. I.F. } d x+c \\ & \Rightarrow \quad y \times e^{-x}=\int 1 . e^{-x} d x+c \\ & \Rightarrow \quad y \cdot e^{-x}=-e^{-x}+c \\ & \text{ Put } x=0, y=1 \\ & \Rightarrow \quad 1 \cdot e^{0}=-e^{0}+c \\ & \Rightarrow \quad 1=-1+c \quad \therefore c=2 \end{aligned} $
So the equation is $y \cdot e^{-x}=-e^{-x}+2$
$ \Rightarrow \quad y=-1+2 e^{x}=2 e^{x}-1 $
Hence, the correct option is $(d)$.
-
Option (a): ( x y = -e^{x} )
- This option is incorrect because it does not satisfy the given differential equation (\frac{d y}{d x} - y = 1). When you differentiate ( y = -\frac{e^{x}}{x} ) and substitute it back into the differential equation, it does not hold true.
-
Option (b): ( x y = -e^{-x} )
- This option is incorrect because it does not satisfy the given differential equation (\frac{d y}{d x} - y = 1). When you differentiate ( y = -\frac{e^{-x}}{x} ) and substitute it back into the differential equation, it does not hold true.
-
Option (c): ( x y = -1 )
- This option is incorrect because it does not satisfy the given differential equation (\frac{d y}{d x} - y = 1). When you differentiate ( y = -\frac{1}{x} ) and substitute it back into the differential equation, it does not hold true.
45. The number of solutions of $\frac{d y}{d x}=\frac{y+1}{x-1}$ when $y(1)=2$ is
(a) none
(b) one
(c) two
(d) infinite
Show Answer
Solution
The given differential equation is $\frac{d y}{d x}=\frac{y+1}{x-1}$
$ \Rightarrow \quad \frac{d y}{y+1}=\frac{d x}{x-1} $
Integrating both sides, we get
$\int \frac{d y}{y+1}=\int \frac{d x}{x-1}$
$\Rightarrow \log (y+1)=\log (x-1)+\log c $
$\Rightarrow \quad \log (y+1)-\log (x-1)=\log c$
$\Rightarrow \log |\frac{y+1}{x-1}|=\log c $
$\Rightarrow \frac{y+1}{x-1}=c \text{ Put } x=1 \text{ and } y=2$
$\Rightarrow \frac{2+1}{1-1}=c \quad \therefore c=\infty$
$\therefore \frac{y+1}{x-1}=\frac{1}{0} \Rightarrow x-1=0 \Rightarrow x=1$
Hence, the correct option is $(b)$.
-
Option (a) none: This option is incorrect because the differential equation does have a solution. The process of solving the differential equation shows that there is at least one solution that satisfies the initial condition ( y(1) = 2 ).
-
Option (c) two: This option is incorrect because the differential equation does not yield two distinct solutions. The integration and application of the initial condition lead to a unique solution.
-
Option (d) infinite: This option is incorrect because the differential equation does not yield an infinite number of solutions. The integration and application of the initial condition result in a specific, unique solution.
46. Which of the following is a second order differential equation?
(a) $(y^{\prime})^{2}+x=y^{2}$
(c) $y^{\prime \prime}+(y^{\prime \prime})^{2}+y=0$
(b) $y^{\prime} y^{\prime \prime}+y=\sin x$
(d) $y^{\prime}=y^{2}$
Show Answer
Solution
Second order differential equation is $y^{\prime} y^{\prime \prime}+y=\sin x$ Hence, the correct option is $(b)$.
-
Option (a) $(y^{\prime})^{2}+x=y^{2}$ is incorrect because it is a first order differential equation. The highest derivative present is $y’$, which is the first derivative of $y$.
-
Option (c) $y^{\prime \prime}+(y^{\prime \prime})^{2}+y=0$ is incorrect because it is a second order differential equation, but it is not the only second order differential equation in the list. The question asks for identifying a second order differential equation, and option (b) is also a second order differential equation.
-
Option (d) $y^{\prime}=y^{2}$ is incorrect because it is a first order differential equation. The highest derivative present is $y’$, which is the first derivative of $y$.
47. Integrating factor of the differential equation
$ (1-x^{2}) \frac{d y}{d x}-x y=1 \text{ is } $
(a) $-x$
(b) $\frac{x}{1+x^{2}}$
(c) $\sqrt{1-x^{2}}$
(d) $\frac{1}{2} \log (1-x^{2})$
Show Answer
Solution
The given differential equation is
$ \begin{aligned} & (1-x^{2}) \frac{d y}{d x}-x y=1 \\ \Rightarrow \quad & \frac{d y}{d x}-\frac{x}{1-x^{2}} \cdot y=\frac{1}{1-x^{2}} \end{aligned} $
Here, $P=-\frac{x}{1-x^{2}}$ and $Q=\frac{1}{1-x^{2}}$
$\therefore$ Integrating factor
$ \text{ I.F. }=e^{\int P d x}=e^{\int \frac{-x}{1-x^{2}} d x}=e^{\frac{1}{2} \log (1-x^{2})}=\sqrt{1-x^{2}} $
Hence, the correct option is (c).
-
Option (a) $-x$: This is incorrect because the integrating factor is derived from the exponential of the integral of $P$, which is $-\frac{x}{1-x^{2}}$. The integral of this function does not result in $-x$.
-
Option (b) $\frac{x}{1+x^{2}}$: This is incorrect because the integrating factor should be derived from the integral of $P = -\frac{x}{1-x^{2}}$. The integral of $-\frac{x}{1-x^{2}}$ does not yield $\frac{x}{1+x^{2}}$.
-
Option (d) $\frac{1}{2} \log (1-x^{2})$: This is incorrect because while $\frac{1}{2} \log (1-x^{2})$ appears in the exponent of the integrating factor, the integrating factor itself is the exponential of this term, which simplifies to $\sqrt{1-x^{2}}$. Thus, $\frac{1}{2} \log (1-x^{2})$ is not the integrating factor but rather part of the exponent in its derivation.
48. $\tan ^{-1} x+\tan ^{-1} y=c$ is the general solution of the differential equation:
(a) $\frac{d y}{d x}=\frac{1+y^{2}}{1+x^{2}}$
(b) $\frac{d y}{d x}=\frac{1+x^{2}}{1+y^{2}}$
(c) $(1+x^{2}) d y+(1+y^{2}) d x=0$
(d) $(1+x^{2}) d x+(1+y^{2}) d y=0$
Show Answer
Solution
Given equation is $\tan ^{-1} x+\tan ^{-1} y=c$
Differentiating w.r.t. $x$, we have
$ \begin{aligned} \frac{1}{1+x^{2}}+\frac{1}{1+y^{2}} \cdot \frac{d y}{d x} & =0 \\ \Rightarrow \quad(\frac{1}{1+y^{2}}) \frac{d y}{d x}=-(\frac{1}{1+x^{2}}) & \Rightarrow \frac{d y}{d x}=-(\frac{1+y^{2}}{1+x^{2}}) \\ \Rightarrow \quad(1+x^{2}) d y & =-(1+y^{2}) d x \\ \Rightarrow \quad(1+x^{2}) d y+(1+y^{2}) d x & =0 \end{aligned} $
Hence the correct option is (c).
-
Option (a): The given differential equation $\frac{d y}{d x}=\frac{1+y^{2}}{1+x^{2}}$ does not match the derived differential equation $\frac{d y}{d x}=-(\frac{1+y^{2}}{1+x^{2}})$. The sign is incorrect, as the correct equation has a negative sign.
-
Option (b): The given differential equation $\frac{d y}{d x}=\frac{1+x^{2}}{1+y^{2}}$ is not equivalent to the derived differential equation $\frac{d y}{d x}=-(\frac{1+y^{2}}{1+x^{2}})$. The numerator and denominator are swapped, and the sign is incorrect.
-
Option (d): The given differential equation $(1+x^{2}) d x+(1+y^{2}) d y=0$ does not match the derived differential equation $(1+x^{2}) d y+(1+y^{2}) d x=0$. The terms involving $dx$ and $dy$ are incorrectly placed.
49. The differential equation $y \frac{d y}{d x}+x=c$ represents:
(a) Family of hyperbolas
(c) Family of ellipses
(b) Family of parabolas
(d) Family of circles
Show Answer
Solution
Given differential equation is
$ \begin{aligned} y \frac{d y}{d x}+x & =c \\ \Rightarrow \quad y \frac{d y}{d x} & =c-x \quad \Rightarrow y d y=(c-x) d x \end{aligned} $
$\therefore$ Integrating both sides, we get
$\int y d y =\int(c-x) d x$
$\Rightarrow \frac{y^{2}}{2} =c x-\frac{x^{2}}{2}+k\Rightarrow \frac{x^{2}}{2}+\frac{y^{2}}{2}-c x=k$
$\Rightarrow x^{2}+y^{2}-2 c x =2 k \text{ which is a family of circles. }$
Hence, the correct option is (d).
-
Option (a) Family of hyperbolas: The general equation of a hyperbola is of the form (\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1) or (\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1). The given differential equation, when integrated, results in an equation of the form (x^2 + y^2 - 2cx = 2k), which does not match the standard form of a hyperbola.
-
Option (b) Family of parabolas: The general equation of a parabola is of the form (y^2 = 4ax) or (x^2 = 4ay). The integrated form of the given differential equation (x^2 + y^2 - 2cx = 2k) does not resemble the standard form of a parabola.
-
Option (c) Family of ellipses: The general equation of an ellipse is of the form (\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1). The integrated form of the given differential equation (x^2 + y^2 - 2cx = 2k) does not match the standard form of an ellipse.
50. The general solution of $e^{x} \cos y d x-e^{x} \sin y d y=0$ is:
(a) $e^{x} \cos y=k$
(b) $e^{x} \sin y=k$
(c) $e^{x}=k \cos y$
(d) $e^{x}=k \sin y$
Show Answer
Solution
The given differential equation is
$ e^{x} \cos y d x-e^{x} \sin y d y=0 $
$\Rightarrow e^{x}(\cos y d x-\sin y d y)=0$
$\Rightarrow \quad \cos y d x-\sin y d y=0$
$\Rightarrow \quad \sin y d y=\cos y d x \Rightarrow \frac{\sin y}{\cos y} d y=d x$
Integrating both sides, we have
$ \begin{aligned} \int \frac{\sin y}{\cos y} d y & =\int d x \\ \Rightarrow \quad-\log |\cos y| & =x+\log k \Rightarrow \log \frac{1}{\cos y}-\log k=x \\ \Rightarrow \quad \log (\frac{1}{k \cos y}) & =x \Rightarrow \frac{1}{k \cos y}=e^{x} \\ \Rightarrow \quad \frac{1}{k} & =e^{x} \cos y \Rightarrow e^{x} \cos y=c \quad[c=\frac{1}{k}] \end{aligned} $
Hence, the correct option is (a).
-
Option (b) ( e^{x} \sin y = k ): This option is incorrect because the integration process and the resulting equation do not lead to ( e^{x} \sin y ). The correct integration results in ( e^{x} \cos y = c ), not involving ( \sin y ).
-
Option (c) ( e^{x} = k \cos y ): This option is incorrect because it suggests that ( e^{x} ) is directly proportional to ( \cos y ) with a constant ( k ). However, the correct form after integration is ( e^{x} \cos y = c ), indicating a product relationship rather than a direct proportionality.
-
Option (d) ( e^{x} = k \sin y ): This option is incorrect because it implies a direct relationship between ( e^{x} ) and ( \sin y ), which does not arise from the integration of the given differential equation. The correct relationship involves ( \cos y ) and not ( \sin y ).
51. The degree of the differential equation:
$ \frac{d^{2} y}{d x^{2}}+(\frac{d y}{d x})^{3}+6 y^{5}=0 \text{ is } $
(a) 1
(b) 2
(c) 3
(d) 5
Show Answer
Solution
The degree of the given differential equation is 1 as the power of the highest order is 1.
Hence, the correct option is $(a)$.
-
Option (b) is incorrect because the degree of the differential equation is not 2. The degree is determined by the power of the highest order derivative, which in this case is (\frac{d^2 y}{dx^2}) raised to the power of 1.
-
Option (c) is incorrect because the degree of the differential equation is not 3. The degree is determined by the power of the highest order derivative, and (\frac{d^2 y}{dx^2}) is raised to the power of 1, not 3.
-
Option (d) is incorrect because the degree of the differential equation is not 5. The degree is determined by the power of the highest order derivative, and (\frac{d^2 y}{dx^2}) is raised to the power of 1, not 5.
52. The solution of the differential equation
$ \frac{d y}{d x}+y=e^{-x}, y(0)=0 \text{ is } $
(a) $y=e^{x}(x-1)$
(c) $y=x e^{-x}+1$
(b) $y=x e^{-x}$
(d) $y=(x+1) e^{-x}$
Show Answer
Solution
The given differential equation is
$ \frac{d y}{d x}+y=e^{-x} $
Since, it is a linear differential equation
$\therefore P=1$ and $Q=e^{-x}$
$\therefore$ I.F $=e^{\int 1 . d x}=e^{x}$
So, the solution is
$ \begin{aligned} & \quad y \times \text{ I.F. }=\int Q \cdot \text{ I.F. } d x+c \Rightarrow y \cdot e^{x}=\int e^{-x} \cdot e^{x} d x+c \\ & \Rightarrow \quad y \cdot e^{x}=\int 1 \cdot d x+c \Rightarrow y \cdot e^{x}=x+c \\ & \text{ Put } x=0, y=0, \text{ we have } 0=0+c \quad \therefore c=0 \end{aligned} $
So, the solution is $y e^{x}=x \Rightarrow y=x \cdot e^{-x}$
Hence, the correct option is (b).
-
Option (a) $y=e^{x}(x-1)$: This option is incorrect because when you substitute $y=e^{x}(x-1)$ into the differential equation $\frac{d y}{d x}+y=e^{-x}$, it does not satisfy the equation. Specifically, the derivative $\frac{d y}{d x}$ of $y=e^{x}(x-1)$ is $e^{x}(x-1) + e^{x} = e^{x}x$, and adding $y$ to this derivative does not yield $e^{-x}$.
-
Option (c) $y=x e^{-x}+1$: This option is incorrect because it does not satisfy the initial condition $y(0)=0$. When $x=0$, $y=x e^{-x}+1$ evaluates to $1$, not $0$. Therefore, it cannot be the correct solution.
-
Option (d) $y=(x+1) e^{-x}$: This option is incorrect because when you substitute $y=(x+1) e^{-x}$ into the differential equation $\frac{d y}{d x}+y=e^{-x}$, it does not satisfy the equation. Specifically, the derivative $\frac{d y}{d x}$ of $y=(x+1) e^{-x}$ is $-x e^{-x}$, and adding $y$ to this derivative does not yield $e^{-x}$.
53. Integrating factor of the differential equation
$ \frac{d y}{d x}+y \tan x-\sec x=0 \text{ is } $
(a) $\cos x$
(b) $\sec x$
(c) $e^{\cos x}$
(d) $e^{\sec x}$
Show Answer
Solution
Given differential equation is
$ \frac{d y}{d x}+y \tan x-\sec x=0 \Rightarrow \frac{d y}{d x}+y \tan x=\sec x $
Here, $P=\tan x$ and $Q=\sec x$
$\therefore$ I.F. $=e^{\int P d x}=e^{\int \tan x d x}=e^{\log \sec x}=\sec x$
Hence, the correct option is (b).
-
Option (a) $\cos x$: This is incorrect because the integrating factor is derived from the exponential of the integral of $P$, which is $\tan x$. The integral of $\tan x$ is $\log \sec x$, and exponentiating this gives $\sec x$, not $\cos x$.
-
Option (c) $e^{\cos x}$: This is incorrect because the integrating factor should be $e^{\int \tan x , dx}$, which simplifies to $e^{\log \sec x} = \sec x$. The expression $e^{\cos x}$ does not relate to the integral of $\tan x$.
-
Option (d) $e^{\sec x}$: This is incorrect because the integrating factor is derived from $e^{\int \tan x , dx}$, which simplifies to $e^{\log \sec x} = \sec x$. The expression $e^{\sec x}$ is not the result of integrating $\tan x$.
54. The solution of the differential equation
$ \frac{d y}{d x}=\frac{1+y^{2}}{1+x^{2}} \text{ is } $
(a) $y=\tan ^{-1} x$
(b) $y-x=k(1+x y)$
(c) $x=\tan ^{-1} y$
(d) $\tan (x y)=k$
Show Answer
Solution
The given differential equation is
$ \frac{d y}{d x}=\frac{1+y^{2}}{1+x^{2}} \Rightarrow \frac{d y}{1+y^{2}}=\frac{d x}{1+x^{2}} $
Integrating both sides, we get
$\int \frac{d y}{1+y^{2}} =\int \frac{d x}{1+x^{2}}$
$\Rightarrow \tan ^{-1} y =\tan ^{-1} x+c \Rightarrow \tan ^{-1} y-\tan ^{-1} x=c$
$\Rightarrow \tan^{-1}(\frac{y-x}{1+x y}) =c$
$\Rightarrow \frac{y-x}{1+x y} =\tan c \Rightarrow \frac{y-x}{1+x y}=k \quad[k=\tan c]$
$\Rightarrow y-x =k(1+x y)$
Hence, the correct option is $(b)$.
-
Option (a) $y=\tan^{-1} x$: This option suggests that the solution to the differential equation is a direct inverse tangent function of (x). However, upon integrating both sides of the given differential equation, we obtain a relationship involving both (y) and (x) with an arbitrary constant (c). The solution is not a simple inverse tangent function of (x) alone, but rather a more complex relationship involving both variables.
-
Option (c) $x=\tan^{-1} y$: This option implies that (x) is the inverse tangent of (y). Similar to option (a), this does not satisfy the form of the solution derived from the integration process. The correct solution involves both (x) and (y) in a combined form, not as a simple inverse tangent function of one variable.
-
Option (d) $\tan(x y)=k$: This option suggests that the product (xy) is related to a constant (k) through the tangent function. However, the integration of the given differential equation results in a linear relationship between (y) and (x) involving an arbitrary constant (k). The correct form of the solution is (y - x = k(1 + xy)), which is not equivalent to (\tan(x y) = k).
55. The integrating factor of the differential equation
$ \frac{d y}{d x}+y=\frac{1+y}{x} \text{ is: } $
(a) $\frac{x}{e^{x}}$
(b) $\frac{e^{x}}{x}$
(c) $x e^{x}$
(d) $e^{x}$
Show Answer
Solution
The given differential equation is
$ \frac{d y}{d x}+y=\frac{1+y}{x} $
$\begin{matrix} \Rightarrow & \frac{d y}{d x}=\frac{1+y}{x}-y \\ \Rightarrow & \frac{d y}{d x}=\frac{1}{x}+y \frac{(1-x)}{x} \Rightarrow \frac{d y}{d x}-(\frac{1-x}{x}) y=\frac{1}{x}\end{matrix} $
Here, $P=-(\frac{1-x}{x})$ and $Q=\frac{1}{x}$
$\therefore$ Integrating factor I.F. $=e^{\int P d x}=e^{\int \frac{x-1}{x} d x}=e^{\int(1-\frac{1}{x}) d x}$
$ =e^{(x-\log x)}=e^{x} \cdot e^{-\log x} $
$ =e^{x} \cdot e^{\log \frac{1}{x}}=e^{x} \cdot \frac{1}{x} $
Hence, the correct option is $(b)$.
-
Option (a) $\frac{x}{e^{x}}$: This option is incorrect because the integrating factor derived from the given differential equation is ( e^{x} \cdot \frac{1}{x} ), not ( \frac{x}{e^{x}} ). The correct integrating factor involves the exponential function in the numerator and ( x ) in the denominator, not the other way around.
-
Option (c) $x e^{x}$: This option is incorrect because the integrating factor should simplify to ( e^{x} \cdot \frac{1}{x} ). The presence of ( x e^{x} ) suggests a multiplication of ( x ) and ( e^{x} ), which does not match the derived integrating factor.
-
Option (d) $e^{x}$: This option is incorrect because the integrating factor must account for the ( \frac{1}{x} ) term in the denominator. The correct integrating factor is ( e^{x} \cdot \frac{1}{x} ), which includes the ( \frac{1}{x} ) term, whereas ( e^{x} ) alone does not.
56. $y=a e^{m x}+b e^{-m x}$ satisfies which of the following differential equations?
(a) $\frac{d y}{d x}+m y=0$
(b) $\frac{d y}{d x}-m y=0$
(c) $\frac{d^{2} y}{d x^{2}}-m^{2} y=0$
(d) $\frac{d^{2} y}{d x^{2}}+m^{2} y=0$
Show Answer
Solution
The given equation is $y=a e^{m x}+b e^{-m x}$
On differentiation, we get $\frac{d y}{d x}=a \cdot m e^{m x}-b \cdot m e^{-m x}$
Again differentiating w.r.t., we have
$ \begin{aligned} & \frac{d^{2} y}{d x^{2}}=a m^{2} e^{m x}+b m^{2} e^{-m x} \\ \Rightarrow & \frac{d^{2} y}{d x^{2}}=m^{2}(a e^{m x}+b e^{-m x}) \Rightarrow \frac{d^{2} y}{d x^{2}}=m^{2} y \Rightarrow \frac{d^{2} y}{d x^{2}}-m^{2} y=0 \end{aligned} $
Hence, the correct option is (c).
-
Option (a): The differential equation (\frac{d y}{d x} + m y = 0) implies that the first derivative of (y) plus (m) times (y) should equal zero. However, for (y = a e^{m x} + b e^{-m x}), the first derivative is (\frac{d y}{d x} = a m e^{m x} - b m e^{-m x}). Substituting this into the equation gives (a m e^{m x} - b m e^{-m x} + m (a e^{m x} + b e^{-m x}) = 0), which simplifies to (2 a m e^{m x} \neq 0) (unless (a = 0) and (b = 0), which is not generally true). Therefore, this option is incorrect.
-
Option (b): The differential equation (\frac{d y}{d x} - m y = 0) implies that the first derivative of (y) minus (m) times (y) should equal zero. For (y = a e^{m x} + b e^{-m x}), the first derivative is (\frac{d y}{d x} = a m e^{m x} - b m e^{-m x}). Substituting this into the equation gives (a m e^{m x} - b m e^{-m x} - m (a e^{m x} + b e^{-m x}) = 0), which simplifies to (-2 b m e^{-m x} \neq 0) (unless (a = 0) and (b = 0), which is not generally true). Therefore, this option is incorrect.
-
Option (d): The differential equation (\frac{d^{2} y}{d x^{2}} + m^{2} y = 0) implies that the second derivative of (y) plus (m^2) times (y) should equal zero. For (y = a e^{m x} + b e^{-m x}), the second derivative is (\frac{d^{2} y}{d x^{2}} = a m^2 e^{m x} + b m^2 e^{-m x}). Substituting this into the equation gives (a m^2 e^{m x} + b m^2 e^{-m x} + m^2 (a e^{m x} + b e^{-m x}) = 0), which simplifies to (2 a m^2 e^{m x} + 2 b m^2 e^{-m x} \neq 0) (unless (a = 0) and (b = 0), which is not generally true). Therefore, this option is incorrect.
57. The solution of the differential equation $\cos x \sin y d x+\sin x \cos y d y=0$ is
(a) $\frac{\sin x}{\sin y}=c$
(b) $\sin x \sin y=c$
(c) $\sin x+\sin y=c$
(d) $\cos x \cos y=c$
Show Answer
Solution
The given differential equation is $\cos x \sin y d x+\sin x \cos y d y=0$
$\Rightarrow \quad \sin x \cos y d y=-\cos x \sin y d x$
$\Rightarrow \frac{\cos y}{\sin y} d y=-\frac{\cos x}{\sin x} d x \Rightarrow \cot y d y=-\cot x d x$
Integrating both sides, we have
$\Rightarrow \quad \int \cot y d y=-\int \cot x d x$
$ \begin{aligned} & \Rightarrow \quad \log |\sin y|=-\log |\sin x|+\log c \\ & \Rightarrow \quad \log |\sin y|+\log |\sin x|=\log c \\ & \Rightarrow \quad \log |\sin y \cdot \sin x|=\log c \Rightarrow \sin x \sin y=c \end{aligned} $
Hence, the correct option is (b).
-
Option (a): $\frac{\sin x}{\sin y}=c$ is incorrect because the integration of the given differential equation leads to a product of $\sin x$ and $\sin y$, not a ratio. The correct form involves the product $\sin x \sin y$, not their quotient.
-
Option (c): $\sin x+\sin y=c$ is incorrect because the integration of the given differential equation results in a logarithmic relationship involving the product of $\sin x$ and $\sin y$. The sum of $\sin x$ and $\sin y$ does not appear in the solution derived from the differential equation.
-
Option (d): $\cos x \cos y=c$ is incorrect because the differential equation involves $\sin x$ and $\sin y$ in its terms. The integration process shows that the solution is related to the product of $\sin x$ and $\sin y$, not $\cos x$ and $\cos y$.
58. The solution of $x \frac{d y}{d x}+y=e^{x}$ is:
(a) $y=\frac{e^{x}}{x}+\frac{k}{x}$
(b) $y=x e^{x}+c x$
(c) $y=x \cdot e^{x}+k$
(d) $x=\frac{e^{y}}{y}+\frac{k}{y}$
Show Answer
Solution
The given differential equation is $x \frac{d y}{d x}+y=e^{x}$
$\Rightarrow \quad \frac{d y}{d x}+\frac{y}{x}=\frac{e^{x}}{x}$
Here $P=\frac{1}{x}$ and $Q=\frac{e^{x}}{x}$
$\therefore$ Integrating factor I.F. $=e^{\int \frac{1}{x} d x}=e^{\log |x|}=x$
So, the solution is
$ \begin{aligned} y \times \text{ I.F. } & =\int Q \times \text{ I.F. } d x+k \Rightarrow y \times x=\int \frac{e^{x}}{x} \times x d x+k \\ \Rightarrow y \times x & =\int e^{x} d x+k \Rightarrow y \times x=e^{x}+k \\ \therefore y & =\frac{e^{x}}{x}+\frac{k}{x} \end{aligned} $
Hence, the correct option is $(a)$.
-
Option (b) $y=x e^{x}+c x$ is incorrect because it does not satisfy the form of the solution derived from the integrating factor method. The correct solution involves dividing by $x$, which is not reflected in this option.
-
Option (c) $y=x \cdot e^{x}+k$ is incorrect because it does not account for the division by $x$ that is necessary in the solution. The correct solution involves terms of the form $\frac{e^{x}}{x}$ and $\frac{k}{x}$, not $x \cdot e^{x}$.
-
Option (d) $x=\frac{e^{y}}{y}+\frac{k}{y}$ is incorrect because it represents a different equation altogether. The original differential equation involves $x$ and $y$ in a specific relationship that does not match this form. This option does not correspond to the solution of the given differential equation.
59. The differential equation of the family of curves $x^{2}+y^{2}-2 a y=0$, where $a$ is arbitrary constant, is:
(a) $(x^{2}-y^{2}) \frac{d y}{d x}=2 x y$
(b) $2(x^{2}+y^{2}) \frac{d y}{d x}=x y$
(c) $2(x^{2}-y^{2}) \frac{d y}{d x}=x y$
(d) $(x^{2}+y^{2}) \frac{d y}{d x}=2 x y$
Show Answer
Solution
The given equation is
$$ \begin{equation*} x^{2}+y^{2}-2 a y=0 \tag{1} \end{equation*} $$
Differentiating w.r.t. $x$, we have
$ \begin{aligned} & 2 x+2 y \cdot \frac{d y}{d x}-2 a \frac{d y}{d x}=0 \\ & \Rightarrow \quad x+y \frac{d y}{d x}-a \frac{d y}{d x}=0 \quad \Rightarrow \quad x+(y-a) \frac{d y}{d x}=0 \\ & \Rightarrow \quad(y-a) \frac{d y}{d x}=-x \quad \Rightarrow y-a=\frac{-x}{d y / d x} \end{aligned} $
$\Rightarrow \quad a=y+\frac{x}{d y / d x} \Rightarrow a=\frac{y \cdot \frac{d y}{d x}+x}{\frac{d y}{d x}}$ Putting the value of $a$ in eq. (1) we get
$ \begin{aligned} & x^{2}+y^{2}-2 y[\frac{y \frac{d y}{d x}+x}{\frac{d y}{d x}}]=0 \\ & \Rightarrow \quad(x^{2}+y^{2}) \frac{d y}{d x}-2 y(y \frac{d y}{d x}+x)=0 \\ & \Rightarrow \quad(x^{2}+y^{2}) \frac{d y}{d x}-2 y^{2} \frac{d y}{d x}-2 x y=0 \\ & \Rightarrow \quad(x^{2}+y^{2}-2 y^{2}) \frac{d y}{d x}=2 x y \Rightarrow(x^{2}-y^{2}) \frac{d y}{d x}=2 x y \end{aligned} $
$\therefore$ Hence the correct option is $(a)$.
-
Option (b): The equation (2(x^{2}+y^{2}) \frac{d y}{d x}=x y) is incorrect because, after differentiating the given equation and substituting the value of (a), the correct form involves ((x^{2}-y^{2})) on the left-hand side, not ((x^{2}+y^{2})). The correct differential equation should balance the terms correctly, which this option does not.
-
Option (c): The equation (2(x^{2}-y^{2}) \frac{d y}{d x}=x y) is incorrect because the factor on the right-hand side should be (2 x y) instead of (x y). The correct differential equation derived from the given family of curves involves a factor of 2 on the right-hand side.
-
Option (d): The equation ((x^{2}+y^{2}) \frac{d y}{d x}=2 x y) is incorrect because, similar to option (b), the left-hand side should involve ((x^{2}-y^{2})) instead of ((x^{2}+y^{2})). The correct differential equation must reflect the proper balance of terms derived from the original equation.
60. Family $y=A x+A^{3}$ of curves will correspond to a differential equation of order
(a) 3
(b) 2
(c) 1
(d) not defined
Show Answer
Solution
The given equation is
$ y=A x+A^{3} $
Differentiating both sides, we get $\frac{d y}{d x}=A$
Again differentiating both sides, we have $\frac{d^{2} y}{d x^{2}}=0$
So the order of the differential equation is 2 .
Hence, the correct option is $(b)$.
-
Option (a) 3: This option is incorrect because the given family of curves results in a second-order differential equation, not a third-order one. The highest derivative present in the differential equation is the second derivative, (\frac{d^2 y}{d x^2} = 0).
-
Option (c) 1: This option is incorrect because the given family of curves results in a second-order differential equation, not a first-order one. The first derivative, (\frac{d y}{d x} = A), is not sufficient to describe the family of curves completely; the second derivative is also needed.
-
Option (d) not defined: This option is incorrect because the order of the differential equation is clearly defined. The highest derivative present in the differential equation is the second derivative, (\frac{d^2 y}{d x^2} = 0), which means the order is 2.
61. The general solution of $\frac{d y}{d x}=2 x e^{x^{2}-y}$ is :
(a) $e^{x^{2}-y}=c$
(c) $e^{y}=e^{x^{2}}+c$
(b) $e^{-y}+e^{x^{2}}=c$
(d) $e^{x^{2}+y}=c$
Show Answer
Solution
The given differential equation is
$ \begin{aligned} \frac{d y}{d x} & =2 x \cdot e^{x^{2}-y} \\ \Rightarrow \quad \frac{d y}{d x} & =2 x \cdot e^{x^{2}} \cdot e^{-y} \Rightarrow \frac{d y}{e^{-y}}=2 x \cdot e^{x^{2}} d x \end{aligned} $
Integrating both sides, we have
$ \begin{aligned} \int \frac{d y}{e^{-y}}=\int 2 x \cdot e^{x^{2}} d x \Rightarrow & \int e^{y} d y=\int 2 x \cdot e^{x^{2}} d x \\ & \text{ Put in RHS } x^{2}=t \therefore 2 x d x=d t \end{aligned} $
$ \begin{aligned} \therefore \quad \int e^{y} d y & =\int e^{t} d t \\ \Rightarrow \quad e^{y} & =e^{t}+c \Rightarrow e^{y}=e^{x^{2}}+c \end{aligned} $
Hence, the correct option is (c).
-
Option (a) $e^{x^{2}-y}=c$: This option suggests that the solution is in the form of $e^{x^{2}-y}$ being a constant. However, integrating the given differential equation correctly shows that the solution involves $e^{y}$ and $e^{x^{2}}$ separately, not combined in the exponent as $x^{2} - y$.
-
Option (b) $e^{-y}+e^{x^{2}}=c$: This option implies that the sum of $e^{-y}$ and $e^{x^{2}}$ is a constant. The correct integration process shows that the solution involves $e^{y}$ and $e^{x^{2}}$ in an additive form, not $e^{-y}$.
-
Option (d) $e^{x^{2}+y}=c$: This option suggests that the solution is in the form of $e^{x^{2}+y}$ being a constant. The correct integration process shows that the solution involves $e^{y}$ and $e^{x^{2}}$ separately, not combined in the exponent as $x^{2} + y$.
62. The curve for which the slope of the tangent at any point is equal to the ratio of the abscissa to the ordinate of the point is:
(a) an ellipse
(b) parabola
(c) circle
(d) rectangular hyperbola
Show Answer
Solution
Since, the slope of the tangent to the curve $=x: y$
$ \therefore \quad \frac{d y}{d x}=\frac{x}{y} \Rightarrow y d y=x d x $
Integrating both sides, we get $\int y d y=\int x d x$
$ \begin{aligned} & \Rightarrow \quad \frac{y^{2}}{2}=\frac{x^{2}}{2}+c \Rightarrow y^{2}=x^{2}+2 c \\ & \Rightarrow \quad y^{2}-x^{2}=2 c=k \text{ which is rectangular hyperbola. } \end{aligned} $
Hence, the correct option is $(d)$.
-
Ellipse: An ellipse is defined by the equation (\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1). The slope of the tangent to an ellipse at any point ((x, y)) is not given by the ratio of the abscissa to the ordinate of the point. Therefore, the condition (\frac{dy}{dx} = \frac{x}{y}) does not hold for an ellipse.
-
Parabola: A parabola is typically defined by the equation (y = ax^2 + bx + c) or (x = ay^2 + by + c). The slope of the tangent to a parabola at any point ((x, y)) is not given by the ratio of the abscissa to the ordinate of the point. Therefore, the condition (\frac{dy}{dx} = \frac{x}{y}) does not hold for a parabola.
-
Circle: A circle is defined by the equation (x^2 + y^2 = r^2). The slope of the tangent to a circle at any point ((x, y)) is not given by the ratio of the abscissa to the ordinate of the point. Therefore, the condition (\frac{dy}{dx} = \frac{x}{y}) does not hold for a circle.
63. The general solution of the differential equation $\frac{d y}{d x}=e^{\frac{x^{2}}{2}}+x y$ is:
(a) $y=c \cdot e^{\frac{-x^{2}}{2}}$
(c) $y=(x+c) \cdot e^{\overline{2}}$
(b) $y=c \cdot e^{\frac{x^{2}}{2}}$
(d) $y=(c-x) e^{\overline{2}}$
Show Answer
Solution
The given differential equation is
$ \frac{d y}{d x}=e^{\frac{x^{2}}{2}}+x y \Rightarrow \frac{d y}{d x}-x y=e^{\frac{x^{2}}{2}} $
Since it is linear differential equation where $P=-x$ and $Q=e^{\frac{x^{2}}{2}}$
$\therefore$ Integrating factor I.F. $=e^{\int P d x}=e^{\int-x d x}=e^{-\frac{x^{2}}{2}}$
So, the solution is
$ \begin{aligned} & y \times \text{ I.F. }=\int Q \times \text{ I.F. } d x+c \\ & \Rightarrow \quad y \times e^{-\frac{x^{2}}{2}}=\int e^{\frac{x^{2}}{2}} e^{-\frac{x^{2}}{2}} d x+c \\ & \Rightarrow \quad y \times e^{-\frac{x^{2}}{2}}=\int e^{0} d x+c \\ & \Rightarrow \quad y \times e^{-\frac{x^{2}}{2}}=\int 1 . d x+c \Rightarrow y \times e^{-\frac{x^{2}}{2}}=x+c \end{aligned} $
$ \therefore \quad y=(x+c) e^{\frac{x^{2}}{2}} $
Hence the correct option is $(c)$.
-
Option (a) $y=c \cdot e^{\frac{-x^{2}}{2}}$: This option is incorrect because it does not satisfy the given differential equation. When substituting $y=c \cdot e^{\frac{-x^{2}}{2}}$ into the differential equation $\frac{d y}{d x}=e^{\frac{x^{2}}{2}}+x y$, the left-hand side will not equal the right-hand side.
-
Option (b) $y=c \cdot e^{\frac{x^{2}}{2}}$: This option is incorrect because it does not satisfy the given differential equation. When substituting $y=c \cdot e^{\frac{x^{2}}{2}}$ into the differential equation $\frac{d y}{d x}=e^{\frac{x^{2}}{2}}+x y$, the left-hand side will not equal the right-hand side.
-
Option (d) $y=(c-x) e^{\overline{2}}$: This option is incorrect because it does not satisfy the given differential equation. The term $e^{\overline{2}}$ is not defined in the context of the problem, and even if it were, the form $(c-x) e^{\overline{2}}$ does not match the structure of the solution derived from the integrating factor method.
64. The solution of the equation $(2 y-1) d x-(2 x+3) d y=0$ is
(a) $\frac{2 x-1}{2 y+3}=k$
(b) $\frac{2 y+1}{2 x-3}=k$
(c) $\frac{2 x+3}{2 y-1}=k$
(d) $\frac{2 x-1}{2 y-1}=k$
Show Answer
Solution
The given differential equation is
$ \begin{aligned} (2 y-1) d x-(2 x+3) d y & =0 \Rightarrow(2 x+3) d y=(2 y-1) d x \\ \Rightarrow \quad \frac{d y}{2 y-1} & =\frac{d x}{2 x+3} \end{aligned} $
Integrating both sides, we get
$ \begin{matrix} \int \frac{d y}{2 y-1} =\int \frac{d x}{2 x+3} \\ \Rightarrow \quad \frac{1}{2} \log |2 y-1| =\frac{1}{2} \log |2 x+3|+\log c \\ \Rightarrow \quad \log |2 y-1| =\log |2 x+3|+2 \log c \\ \Rightarrow \quad \log |2 y-1|-\log |2 x+3| =\log c^{2} \\ \Rightarrow \quad \log |\frac{2 y-1}{2 x+3}| =\log c^{2} \\ \Rightarrow \quad \frac{2 y-1}{2 x+3} =c^{2} \Rightarrow \frac{2 x+3}{2 y-1}=\frac{1}{c^{2}} \\ \Rightarrow \quad \frac{2 x+3}{2 y-1} =k \text{, where } k=\frac{1}{c^{2}} \end{matrix} $
Hence, the correct option is (c).
-
Option (a): (\frac{2 x-1}{2 y+3}=k)
This option is incorrect because the integration of the given differential equation leads to the relationship (\frac{2 y-1}{2 x+3} = c^2). Rearranging this, we get (\frac{2 x+3}{2 y-1} = k), where (k = \frac{1}{c^2}). The expression (\frac{2 x-1}{2 y+3}) does not match the derived relationship.
-
Option (b): (\frac{2 y+1}{2 x-3}=k)
This option is incorrect because it does not correspond to the derived relationship from the differential equation. The correct relationship is (\frac{2 x+3}{2 y-1} = k). The expression (\frac{2 y+1}{2 x-3}) is not derived from the given differential equation and does not match the correct form.
-
Option (d): (\frac{2 x-1}{2 y-1}=k)
This option is incorrect because the integration of the given differential equation results in the relationship (\frac{2 x+3}{2 y-1} = k). The expression (\frac{2 x-1}{2 y-1}) does not match the derived relationship and is not a solution to the given differential equation.
65. The differential equation for which $y=a \cos x+b \sin x$ is a solution, is:
(a) $\frac{d^{2} y}{d x^{2}}+y=0$
(b) $\frac{d^{2} y}{d x^{2}}-y=0$
(c) $\frac{d^{2} y}{d x^{2}}+(a+b) y=0$
(d) $\frac{d^{2} y}{d x^{2}}+(a-b) y=0$
Show Answer
Solution
The given equation is
$ \begin{gathered} y=a \cos x+b \sin x \\ \frac{d y}{d x}=-a \sin x+b \cos x \end{gathered} $
$ \begin{aligned} \frac{d^{2} y}{d x^{2}} & =-a \cos x-b \sin x \\ \Rightarrow \quad \frac{d^{2} y}{d x^{2}} & =-(a \cos x+b \sin x) \Rightarrow \frac{d^{2} y}{d x^{2}}=-y \Rightarrow \frac{d y}{d x}+y=0 \end{aligned} $
Hence, the correct option is $(a)$.
-
Option (b): The differential equation $\frac{d^{2} y}{d x^{2}}-y=0$ implies that the second derivative of ( y ) is equal to ( y ). However, for the given solution ( y = a \cos x + b \sin x ), the second derivative is ( -y ), not ( y ). Therefore, this option is incorrect.
-
Option (c): The differential equation $\frac{d^{2} y}{d x^{2}}+(a+b) y=0$ suggests that the second derivative of ( y ) plus ((a+b) y) equals zero. This would imply that the coefficient of ( y ) in the differential equation depends on the constants ( a ) and ( b ). However, the correct differential equation should be independent of these constants, as shown by the given solution. Therefore, this option is incorrect.
-
Option (d): The differential equation $\frac{d^{2} y}{d x^{2}}+(a-b) y=0$ implies that the second derivative of ( y ) plus ((a-b) y) equals zero. Similar to option (c), this would mean that the coefficient of ( y ) in the differential equation depends on the constants ( a ) and ( b ). The correct differential equation should not depend on these constants. Therefore, this option is incorrect.
66. The solution of $\frac{d y}{d x}+y=e^{-x}, y(0)=0$ is:
(a) $y=e^{-x}(x-1)$
(b) $y=x \cdot e^{x}$
(c) $y=x e^{-x}+1$
(d) $y=x \cdot e^{-x}$
Show Answer
Solution
The given differential equation is $\frac{d y}{d x}+y=e^{-x}$
Since, it is a linear differential equation then $P=1$ and $Q=e^{-x}$
Integrating factor I.F. $=e^{\int P d x}=e^{\int 1 . d x}=e^{x}$
$\therefore$ Solution is
$ \begin{aligned} y \times \text{ I.F. } & =\int Q \times \text{ I.F. } d x+c \\ \Rightarrow \quad y \times e^{x} & =\int e^{-x} \times e^{x} d x+c \Rightarrow y \times e^{x}=\int e^{0} d x+c \\ \Rightarrow \quad y \times e^{x} & =\int 1 . d x+c \Rightarrow y \times e^{x}=x+c \end{aligned} $
Put $y=0$ and $x=0$
$\therefore \quad 0=0+c \quad \therefore \quad c=0$
$\therefore$ equation is $y \times e^{x}=x$
So $\quad y=x \cdot e^{-x}$
Hence, the correct option is $(d)$.
-
Option (a) $y = e^{-x}(x-1)$: This solution does not satisfy the initial condition ( y(0) = 0 ). When ( x = 0 ), ( y = e^{-0}(0-1) = -1 ), which is not equal to 0.
-
Option (b) $y = x \cdot e^{x}$: This solution does not satisfy the differential equation (\frac{d y}{d x} + y = e^{-x}). Substituting ( y = x \cdot e^{x} ) into the differential equation results in (\frac{d}{dx}(x \cdot e^{x}) + x \cdot e^{x} \neq e^{-x}).
-
Option (c) $y = x e^{-x} + 1$: This solution does not satisfy the initial condition ( y(0) = 0 ). When ( x = 0 ), ( y = 0 \cdot e^{-0} + 1 = 1 ), which is not equal to 0.
67. The order and degree of the differential equation
$ [\frac{d^{3} y}{d x^{3}}]^{2}-3 \frac{d^{2} y}{d x^{2}}+2(\frac{d y}{d x})^{4}=y^{4} \text{ are } $
(a) 1,4
(b) 3,4
(c) 2,4
(d) 3,2
Show Answer
Solution
The given differential equation is
$ [\frac{d^{3} y}{d x^{3}}]^{2}-3 \frac{d^{2} y}{d x^{2}}+2(\frac{d y}{d x})^{4}=y^{4} $
Here the highest derivative is $\frac{d^{3} y}{d x^{3}}$.
$\therefore$ the order of the differential equation is 3 and since, the power of highest order is 2
$\therefore$ its degree is 2
Hence, the correct option is (d).
-
Option (a) is incorrect because the order of the differential equation is not 1; it is 3. The highest derivative present in the equation is $\frac{d^{3} y}{d x^{3}}$.
-
Option (b) is incorrect because the degree of the differential equation is not 4; it is 2. The highest power of the highest order derivative $\left(\frac{d^{3} y}{d x^{3}}\right)$ is 2.
-
Option (c) is incorrect because the order of the differential equation is not 2; it is 3. The highest derivative present in the equation is $\frac{d^{3} y}{d x^{3}}$.
68. The order and degree of the differential equation
$[1+(\frac{d y}{d x})^{2}]=\frac{d^{2} y}{d x^{2}}$ are:
(a) $2, \frac{3}{2}$
(b) 2,3
(c) 2, 1
(d) 3, 4
Show Answer
Solution
The given differential equation is
$ [1+(\frac{d y}{d x})^{2}]=\frac{d^{2} y}{d x^{2}} $
Here, the highest derivative is 2 ,
$\therefore$ order $=2$
and the power of the highest derivative is 1
$\therefore$ degree $=1$
Hence, the correct option is (c).
-
Option (a) is incorrect because the degree of the differential equation is not (\frac{3}{2}). The degree is defined as the power of the highest order derivative when the equation is polynomial in derivatives, which in this case is 1.
-
Option (b) is incorrect because the degree of the differential equation is not 3. The degree is 1, as the highest order derivative (\frac{d^2 y}{d x^2}) appears to the power of 1.
-
Option (d) is incorrect because the order of the differential equation is not 3, and the degree is not 4. The order is 2, as the highest derivative is (\frac{d^2 y}{d x^2}), and the degree is 1.
69. The differential equation of the family of curves $y^{2}=4 a(x+a)$ is:
(a) $y^{2}=4 \frac{d y}{d x}(x+\frac{d y}{d x})$
(b) $2 y \cdot \frac{d y}{d x}=4 a$
(c) $y \cdot \frac{d^{2} y}{d x^{2}}+(\frac{d y}{d x})^{2}=0$
(d) $2 x \cdot \frac{d y}{d x}+y(\frac{d y}{d x})^{2}-y$
Show Answer
Solution
The given equation of family of curves is
$$ \begin{align*} & y^{2}=4 a(x+a) \\ \Rightarrow \quad & y^{2}=4 a x+4 a^{2} \tag{1} \end{align*} $$
Differentiating both sides, w.r.t. $x$, we get
$ \begin{aligned} 2 y \cdot \frac{d y}{d x} & =4 a \\ \Rightarrow \quad y \cdot \frac{d y}{d x} & =2 a \Rightarrow \frac{y}{2} \frac{d y}{d x}=a \end{aligned} $
Now, putting the value of $a$ in eq. (1) we get
$ \begin{aligned} y^{2} & =4 x(\frac{y}{2} \frac{d y}{d x})+4(\frac{y}{2} \cdot \frac{d y}{d x})^{2} \\ \Rightarrow \quad y^{2} & =2 x y \frac{d y}{d x}+y^{2}(\frac{d y}{d x})^{2} \Rightarrow y=2 x \frac{d y}{d x}+y(\frac{d y}{d x})^{2} \end{aligned} $
$ \Rightarrow \quad 2 x \cdot \frac{d y}{d x}+y \cdot(\frac{d y}{d x})^{2}-y=0 $
Hence, the correct option is (d).
-
Option (a): The equation $y^{2}=4 \frac{d y}{d x}(x+\frac{d y}{d x})$ is incorrect because it does not correctly represent the relationship derived from the given family of curves. The correct differential equation involves a combination of $x$, $y$, and $\frac{d y}{d x}$ terms that satisfy the original curve equation after differentiation and substitution.
-
Option (b): The equation $2 y \cdot \frac{d y}{d x}=4 a$ is a step in the differentiation process but not the final differential equation. It represents an intermediate result before substituting back into the original equation to eliminate the parameter $a$.
-
Option (c): The equation $y \cdot \frac{d^{2} y}{d x^{2}}+(\frac{d y}{d x})^{2}=0$ involves the second derivative $\frac{d^{2} y}{d x^{2}}$, which is not necessary for the given family of curves. The correct differential equation can be obtained using only the first derivative $\frac{d y}{d x}$.
70. Which of the following is the general solution of
$ \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+y=0 ? $
(a) $y=(A x+B) \cdot e^{x}$
(b) $y=(A x+B) e^{-x}$
(c) $y=A e^{x}+B e^{-x}$
(d) $y=A \cos x+B \sin x$
Show Answer
Solution
The given differential equation is
$ \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+y=0 $
Since the above equation is of second order and first degree
$\therefore \quad D^{2} y-2 D y+y=0$, where $D=\frac{d}{d x}$
$\Rightarrow(D^{2}-2 D+1) y=0$
$\therefore$ auxiliary equation is
$ m^{2}-2 m+1=0 \Rightarrow(m-1)^{2}=0 \Rightarrow m=1,1 $
If the roots of Auxiliary equation are real and equal say $(m)$ then $C F=(c_1 x+c_2) \cdot e^{m x}$
$\therefore \quad C F=(A x+B) e^{x}$
So $y=(A x+B) \cdot e^{x}$
Hence, the correct option is $(a)$.
-
Option (b) $y=(A x+B) e^{-x}$: This solution form suggests that the characteristic equation has a repeated root at $m = -1$. However, the characteristic equation derived from the given differential equation is $(m-1)^2 = 0$, which has a repeated root at $m = 1$, not $m = -1$. Therefore, this form does not satisfy the given differential equation.
-
Option (c) $y=A e^{x}+B e^{-x}$: This solution form suggests that the characteristic equation has distinct roots at $m = 1$ and $m = -1$. However, the characteristic equation derived from the given differential equation is $(m-1)^2 = 0$, which has a repeated root at $m = 1$. Therefore, this form does not satisfy the given differential equation.
-
Option (d) $y=A \cos x+B \sin x$: This solution form suggests that the characteristic equation has complex roots of the form $m = \pm i$. However, the characteristic equation derived from the given differential equation is $(m-1)^2 = 0$, which has a repeated real root at $m = 1$. Therefore, this form does not satisfy the given differential equation.
71. General solution of $\frac{d y}{d x}+y \tan x=\sec x$ is:
(a) $y \sec x=\tan x+c$
(b) $y \tan x=\sec x+c$
(c) $\tan x=y \tan x+c$
(d) $x \sec x=\tan y+c$
Show Answer
Solution
The given differential equation is $\frac{d y}{d x}+y \tan x=\sec x$
Since, it is a linear differential equation
$\therefore \quad P=\tan x$ and $Q=\sec x$
Integrating factor I.F. $=e^{\int P d x}=e^{\int \tan x d x}=e^{\log \sec x}=\sec x$
$\therefore$ Solution is
$ \begin{aligned} y \times \text{ I.F. } & =\int Q \times \text{ I.F. } d x+c \\ \Rightarrow \quad y \times \sec x & =\int \sec x \cdot \sec x d x+c \\ \Rightarrow \quad y \sec x & =\int \sec ^{2} x d x+c \Rightarrow y \sec x=\tan x+c \end{aligned} $
Hence, the correct option is (a).
-
Option (b): $y \tan x=\sec x+c$ is incorrect because the integration of $\sec^2 x$ results in $\tan x$, not $\sec x$. Therefore, the term on the right side of the equation should be $\tan x + c$, not $\sec x + c$.
-
Option (c): $\tan x=y \tan x+c$ is incorrect because it does not properly represent the solution form of a linear differential equation. The correct form should have $y$ multiplied by the integrating factor $\sec x$, not $\tan x$.
-
Option (d): $x \sec x=\tan y+c$ is incorrect because it incorrectly mixes the variables $x$ and $y$. The solution to the differential equation should be in terms of $y$ and $x$, not $x$ and $y$. Additionally, the integrating factor and the integration process do not lead to such a form.
72. Solution of differential equation $\frac{d y}{d x}+\frac{y}{x}=\sin x$ is:
(a) $x(y+\cos x)=\sin x+c$
(b) $x(y-\cos x)=\sin x+c$
(c) $x y \cos x=\sin x+c$
(d) $x(y+\cos x)=\cos x+c$
Show Answer
Solution
The given differential equation is $\frac{d y}{d x}+\frac{y}{x}=\sin x$
Since, it is a linear differential equation
$\therefore \quad P=\frac{1}{x}$ and $Q=\sin x$
Integrating factor I.F. $=e^{\int \frac{1}{x} d x}=e^{\log x}=x$
$\therefore$ Solution is $y \times$ I.F. $=\int Q \times$ I.F. $d x+c$
$ \begin{matrix} y \times x =\int \sin x \cdot x d x+c \Rightarrow y \times x=\int x \sin x d x+c \\ y x =x \cdot \int \sin x d x-\int(D(x) \int \sin x d x) d x+c \\ \Rightarrow y x =x(-\cos x)-\int-\cos x d x \\ \Rightarrow y x=-x \cos x+\int \cos x d x \Rightarrow y x=-x \cos x+\sin x+c \\ \Rightarrow y x+x \cos x =\sin x+c \\ \Rightarrow x(y+\cos x) =\sin x+c \end{matrix} $
Hence, the correct option is $(a)$.
-
Option (b): The expression $x(y-\cos x)=\sin x+c$ is incorrect because the correct solution derived from the linear differential equation is $x(y+\cos x)=\sin x+c$. The sign in front of $\cos x$ should be positive, not negative.
-
Option (c): The expression $x y \cos x=\sin x+c$ is incorrect because it does not match the form of the solution derived from the differential equation. The correct solution involves a sum of $y$ and $\cos x$ multiplied by $x$, not a product of $x$, $y$, and $\cos x$.
-
Option (d): The expression $x(y+\cos x)=\cos x+c$ is incorrect because the right-hand side of the equation should be $\sin x+c$ as derived from the differential equation. The presence of $\cos x$ instead of $\sin x$ on the right-hand side makes this option incorrect.
73. The general solution of the differential equation $(e^{x}+1) y d y=(y+1) e^{x} d x$ is:
(a) $(y+1)=k(e^{x}+1)$
(b) $y+1=e^{x}+1+k$
(c) $y=\log [k(y+1)(e^{x}+1)]$
(d) $y=\log {\frac{e^{x}+1}{y+1}}+k$
Show Answer
Solution
The given differential equation is
$ \begin{aligned} (e^{x}+1) y d y & =(y+1) e^{x} d x \\ \Rightarrow \quad \frac{y}{y+1} d y & =\frac{e^{x}}{e^{x}+1} d x \end{aligned} $
Integrating both sides, we get
$ \begin{aligned} \int \frac{y}{y+1} d y & =\int \frac{e^{x}}{e^{x}+1} d x \\ \Rightarrow \quad \int \frac{y+1-1}{y+1} d y & =\int \frac{e^{x}}{e^{x}+1} d x \\ \Rightarrow \quad \int 1 \cdot d y-\int \frac{1}{y+1} d y & =\int \frac{e^{x}}{e^{x}+1} d x \end{aligned} $
$ \begin{aligned} \Rightarrow & y-\log |y+1| & =\log |e^{x}+1|+\log k \\ \Rightarrow & y & =\log |y+1|+\log |e^{x}+1|+\log k \\ \Rightarrow & y & =\log |k(y+1)(e^{x}+1)| \end{aligned} $
Hence, the correct option is (c).
-
Option (a): $(y+1)=k(e^{x}+1)$
- This option suggests a linear relationship between ( y+1 ) and ( e^{x}+1 ). However, the differential equation involves logarithmic terms after integration, which is not captured by this linear form. The correct solution involves a logarithmic relationship, not a simple linear one.
-
Option (b): $y+1=e^{x}+1+k$
- This option implies that ( y+1 ) is a sum of ( e^{x}+1 ) and a constant ( k ). This form does not satisfy the differential equation after integration, as the correct solution involves a product of terms inside a logarithm, not a simple additive form.
-
Option (d): $y=\log {\frac{e^{x}+1}{y+1}}+k$
- This option suggests a logarithmic relationship but incorrectly places ( y+1 ) in the denominator inside the logarithm. The correct solution involves ( y+1 ) and ( e^{x}+1 ) being multiplied together inside the logarithm, not divided.
74. The solution of differential equation $\frac{d y}{d x}=e^{x-y}+x^{2} e^{-y}$ is:
(a) $y=e^{x-y}-x^{2} e^{-y}+c$
(b) $e^{y}-e^{x}=\frac{x^{3}}{3}+c$
(c) $e^{x}+e^{y}=\frac{x^{3}}{3}+c$
(d) $e^{x}-e^{y}=\frac{x^{3}}{3}+c$
Show Answer
Solution
The given differential equation is
$ \begin{aligned} & \frac{d y}{d x}=e^{x-y}+x^{2} e^{-y} \\ & \Rightarrow \quad \frac{d y}{d x}=e^{x} \cdot e^{-y}+x^{2} \cdot e^{-y} \Rightarrow \frac{d y}{d x}=e^{-y}(e^{x}+x^{2}) \\ & \Rightarrow \quad \frac{d y}{e^{-y}}=(e^{x}+x^{2}) d x \Rightarrow e^{y} \cdot d y=(e^{x}+x^{2}) d x \end{aligned} $
Integrating both sides, we have
$ \begin{aligned} \int e^{y} d y & =\int(e^{x}+x^{2}) d x \\ \Rightarrow \quad e^{y} & =e^{x}+\frac{x^{3}}{3}+c \Rightarrow e^{y}-e^{x}=\frac{x^{3}}{3}+c \end{aligned} $
Hence, the correct option is $(b)$.
-
Option (a): The expression $y = e^{x-y} - x^{2} e^{-y} + c$ is not a valid solution to the given differential equation. The correct solution involves integrating both sides of the equation, which results in an equation involving $e^y$ and $e^x$, not $y$ directly.
-
Option (c): The expression $e^{x} + e^{y} = \frac{x^{3}}{3} + c$ is incorrect because, after integrating both sides of the differential equation, the correct form involves $e^y - e^x$, not $e^y + e^x$. The integration process leads to a subtraction, not an addition.
-
Option (d): The expression $e^{x} - e^{y} = \frac{x^{3}}{3} + c$ is incorrect because the correct solution involves $e^y - e^x$, not $e^x - e^y$. The signs are reversed in this option, which does not match the result obtained from integrating both sides of the differential equation.
75. The solution of the differential equation
$ \frac{d y}{d x}+\frac{2 x y}{1+x^{2}}=\frac{1}{(1+x^{2})^{2}} \text{ is: } $
(a) $y(1+x^{2})=c+\tan ^{-1} x$
(b) $\frac{y}{1+x^{2}}=c+\tan ^{-1} x$
(c) $y \log (1+x^{2})=c+\tan ^{-1} x$
(d) $y(1+x^{2})=c+\sin ^{-1} x$
Show Answer
Solution
The given differential equation is
$ \frac{d y}{d x}+\frac{2 x y}{1+x^{2}}=\frac{1}{(1+x^{2})^{2}} $
Since, it is a linear differential equation
$ P=\frac{2 x}{1+x^{2}} \text{ and } Q=\frac{1}{(1+x^{2})^{2}} $
Integrating factor I.F. $=e^{\int P d x}=e^{\int \frac{2 x}{1+x^{2}} d x}=e^{\log (1+x^{2})}=(1+x^{2})$
$\therefore$ Solution is $y \times$ I.F. $=\int Q \times$ I.F. $d x+c$
$ \begin{aligned} & \Rightarrow \quad y(1+x^{2})=\int \frac{1}{(1+x^{2})^{2}} \times(1+x^{2}) d x+c \\ & \Rightarrow \quad y(1+x^{2})=\int \frac{1}{(1+x^{2})} d x+c \Rightarrow y(1+x^{2})=\tan ^{-1} x+c \end{aligned} $
Hence, the correct option is $(a)$.
-
Option (b): $\frac{y}{1+x^{2}}=c+\tan ^{-1} x$
- This option is incorrect because the solution derived from the integrating factor method results in $y(1+x^{2})=\tan ^{-1} x+c$. Dividing both sides by $(1+x^{2})$ would not yield the form $\frac{y}{1+x^{2}}=c+\tan ^{-1} x$.
-
Option (c): $y \log (1+x^{2})=c+\tan ^{-1} x$
- This option is incorrect because the integrating factor derived is $(1+x^{2})$, not $\log (1+x^{2})$. The solution involves multiplying $y$ by $(1+x^{2})$, not $\log (1+x^{2})$.
-
Option (d): $y(1+x^{2})=c+\sin ^{-1} x$
- This option is incorrect because the integral of $\frac{1}{1+x^{2}}$ is $\tan^{-1} x$, not $\sin^{-1} x$. Therefore, the correct form of the solution involves $\tan^{-1} x$ and not $\sin^{-1} x$.
Fillers
76. Fill in the blanks of the following ( $i$ to $x i$ ):
(i) The degree of the differential equation $\frac{d^{2} y}{d x^{2}}+e^{d y / d x}=0$ is ……
(ii) The degree of the differential equation $\sqrt{1+(\frac{d y}{d x})^{2}}=x$ is ……
(iii) The number of arbitrary constants in the general solution of a differential equation of order three is ……
(iv) $\frac{d y}{d x}+\frac{y}{x \log x}=\frac{1}{x}$ is an equation of the type ……
(v) General solution of the differential equation of the type $\frac{d x}{d y}+P_1 x=Q_1$ is given by ……
(vi) The solution of the differential equation $x \frac{d y}{d x}+2 y=x^{2}$ is ……
(vii) The solution of $(1+x^{2}) \frac{d y}{d x}+2 x y-4 x^{2}=0$ is ……
(viii) The solution of the differential equation $y d x+(x+x y) d y=0$ is ……
(ix) General solution of $\frac{d y}{d x}+y=\sin x$ is ……
( $x$ ) The solution of differential equation $\cot y d x=x d y$ is ……
(xi) The integrating factor of $\frac{d y}{d x}+y=\frac{1+y}{x}$ is ……
Show Answer
Solution
(i) The degree of the differential equation $\frac{d^{2} y}{d x^{2}}+e^{d y / d x}=0$ is not defined.
(ii) The given differential equation is $\sqrt{1+(\frac{d y}{d x})^{2}}=x$ Squaring both sides, we gett
$ 1+(\frac{d y}{d x})^{2}=x^{2} $
So, the degree of the equation is 2 .
(iii) The number of arbitrary constants in the solution is 3 .
(iv) The given differential equation $\frac{d y}{d x}+\frac{y}{x \log x}=\frac{1}{x}$ is of the type $\frac{d y}{d x}+P y=Q$.
(v) General solution of the differential equation of the type $\frac{d x}{d y}+P_1 x=Q_1$ is given by $x \times$ I.F. $=\int Q \times$ I.F. $d y+c$
$\Rightarrow \quad x \cdot e^{\int P_1 d y}=\int Q_1 \cdot e^{\int P_1 d y} d y+c$.
(vi) The given differential equation is $x \frac{d y}{d x}+2 y=x^{2}$
$\Rightarrow \quad \frac{d y}{d x}+\frac{2}{x} y=x$.
Since, it is linear differential equation
$\therefore \quad P=\frac{2}{x}$ and $Q=x$
Integrating factor I.F. $=e^{\int P d x}=e^{\int \frac{2}{x} d x}=e^{2 \log x}=e^{\log x^{2}}=x^{2}$
$\therefore$ Solution is
$ \begin{aligned} y \times \text{ I.F. } & =\int Q \times \text{ I.F. } d x+c \\ \Rightarrow \quad y \cdot x^{2} & =\int x \cdot x^{2} d x+c \quad \Rightarrow y \cdot x^{2}=\int x^{3} d x+c \\ \Rightarrow \quad y \cdot x^{2} & =\frac{1}{4} x^{4}+c \quad \Rightarrow y=\frac{1}{4} x^{2}+c \cdot x^{-2} \end{aligned} $
Hence, the solution is $y=\frac{1}{4} x^{2}+c \cdot x^{-2}$.
(vii) The given differential equation is
$ \begin{aligned} & (1+x^{2}) \frac{d y}{d x}+2 x y-4 x^{2}=0 \\ \Rightarrow \quad & \frac{d y}{d x}+\frac{2 x y}{1+x^{2}}=\frac{4 x^{2}}{1+x^{2}} \end{aligned} $
Since it is a linear differential equation
$\therefore \quad P=\frac{2 x}{1+x^{2}}$ and $Q=\frac{4 x^{2}}{1+x^{2}}$
Integrating factorI.F. $=e^{\int P d x}=e^{\int \frac{2 x}{1+x^{2}} d x}=e^{\log (1+x^{2})}=(1+x^{2})$
$\therefore$ Solution is $y \times I$.F $=\int Q \times$ I.F. $d x+c$
$ \begin{aligned} \Rightarrow y \times(1+x^{2}) =\int \frac{4 x}{1+x^{2}} \times(1+x^{2}) d x+c \\ \Rightarrow y \times(1+x^{2}) =\int 4 x^{2} d x+c \Rightarrow y \times(1+x^{2})=\frac{4}{3} x^{3}+c \\ \Rightarrow y =\frac{4}{3} \frac{x^{3}}{(1+x^{2})}+c(1+x^{2})^{-1} \end{aligned} $
Hence, the required solution is $y=\frac{4}{3} \frac{x^{3}}{(1+x^{2})}+c(1+x^{2})^{-1}$.
(viii) The given differential equation is
$ \begin{gathered} y d x+(x+x y) d y=0 \\ \Rightarrow \quad(x+x y) d y=-y d x \Rightarrow x(1+y) d y=-y d x \\ \Rightarrow \quad \frac{1+y}{y} d y=-\frac{1}{x} d x \end{gathered} $
Integrating both sides, we get
$ \begin{aligned} & \int \frac{1+y}{y} d y=-\int \frac{1}{x} d x \\ & \Rightarrow \quad \int(\frac{1}{y}+1) d y=-\int \frac{1}{x} d x \\ & \Rightarrow \quad \log y+y=-\log x+\log c \\ & \Rightarrow \log x+\log y+\log e^{y}=\log c \\ & \Rightarrow \quad \log (x y \cdot e^{y})=\log c \\ & \therefore \quad x y=c e^{-y} \end{aligned} $
Hence, the required solution is $x y=c e^{-y}$.
(ix) The given differential equation is $\frac{d y}{d x}+y=\sin x$
Since, it it a linear differential equation
$\therefore \quad P=1$ and $Q=\sin x$
Integrating factor I.F. $=e^{\int P d x}=e^{\int 1 . d x}=e^{x}$
$\therefore$ Solution is $y \times$ I.F. $=\int Q \times$ I.F. $d x+c$
$\Rightarrow \quad y \cdot e^{x}=\int \sin x \cdot e^{x} d x+c$
Let $I=\int \sin _{I} x \cdot e^{x} d x$
$ \begin{aligned} & I=\sin x \cdot \int e^{x} d x-\int(D(\sin x) \cdot \int e^{x} d x) d x \\ & I=\sin x \cdot e^{x}-\int \cos x \cdot e^{x} d x \\ & I=\sin x \cdot e^{x}-[\cos x \cdot \int e^{x} d x-\int(D(\cos x) \int e^{x} d x) d x] \end{aligned} $
$ \begin{aligned} I & =\sin x \cdot e^{x}-[\cos x \cdot e^{x}-\int-\sin x \cdot e^{x} d x] \\ I & =\sin x \cdot e^{x}-\cos x \cdot e^{x}-\int \sin x \cdot e^{x} d x \\ I & =\sin x \cdot e^{x}-\cos x \cdot e^{x}-I \\ \Rightarrow I+I & =e^{x}(\sin x-\cos x) \\ \Rightarrow \quad 2 I & =e^{x}(\sin x-\cos x) \\ \therefore \quad I & =\frac{e^{x}}{2}(\sin x-\cos x) \end{aligned} $
From eq. (1) we get
$ \begin{aligned} y \cdot e^{x} & =\frac{e^{x}}{2}(\sin x-\cos x)+c \\ y & =(\frac{\sin x-\cos x}{2})+c \cdot e^{-x} \end{aligned} $
Hence, the required solution is
$ y=(\frac{\sin x-\cos x}{2})+c \cdot e^{-x} $
(x) The given differential equation is $\cot y d x=x d y$
$ \Rightarrow \frac{d y}{\cot y}=\frac{d x}{x} \Rightarrow \tan y d y=\frac{d x}{x} $
Integrating both sides, we get
$ \begin{aligned} & \quad \int \tan y d y=\int \frac{d x}{x} \Rightarrow \log \sec y=\log x+\log c \\ \Rightarrow \quad & \log \sec y-\log x=\log c \\ \Rightarrow \quad & \log |\frac{\sec y}{x}|=\log C \\ \therefore \quad & \frac{\sec y}{x}=C \Rightarrow \frac{x}{\sec y}=\frac{1}{C} \Rightarrow \frac{x}{\sec y}=C \quad[\frac{1}{c}=C] \\ \therefore \quad & x=C \sec y \end{aligned} $
Hence, the required solution is $x=C \sec y$.
$(x i)$ The given differential equation is
$ \begin{aligned} \frac{d y}{d x}+y & =\frac{1+y}{x} \\ \frac{d y}{d x}+y & =\frac{1}{x}+\frac{y}{x} \\ \Rightarrow \quad \frac{d y}{d x}+y-\frac{y}{x} & =\frac{1}{x} \Rightarrow \frac{d y}{d x}+(1-\frac{1}{x}) y=\frac{1}{x} \end{aligned} $
$ \begin{aligned} & \text{ Here } P=(1-\frac{1}{x}) \\ & \therefore \quad \text{ I.F. }=e^{\int P d x}=e^{\int(1-\frac{1}{x}) d x}=e^{(x-\log x)} \\ & =e^{x} \cdot e^{-\log x}=e^{x} \cdot e^{\log \frac{1}{x}}=e^{x} \cdot \frac{1}{x} \end{aligned} $
Hence, the required I.F. $=e^{x} \cdot \frac{1}{x}$.
True/False
77. State True or False for the following:
(i) Integrating factor of the differential equation of the form $\frac{d x}{d y}+P_1 x=Q_1$ is given by $e^{\int P_1 d y}$.
(ii) Solution of the differential equation of the type $\frac{d x}{d y}+P_1 x=Q_1$ is given by $x$. I.F. $=\int$ (I.F.) $Q_1 d y$.
(iii) Correct substitution for the solution of the differential equation of the type $\frac{d y}{d x}=f(x, y)$, where $f(x, y)$ is a homogeneous function of zero degree is $y=v x$.
(iv) Correct substitution for the solution of the differential equation of the type $\frac{d x}{d y}=g(x, y)$, where $g(x, y)$ is a homogeneous function of the degree zero is $x=v y$.
(v) Number of arbitrary constants in the particular solution of a differential equation of order two is two.
(vi) The differential equation representing the family of circles $x^{2}+(y-a)^{2}=a^{2}$ will be of order two.
(vii) The solution of $\frac{d y}{d x}=(\frac{y}{x})^{1 / 3}$ is $y^{2 / 3}-x^{2 / 3}=c$.
(viii) Differential equation representing the family of curves
$ y=e^{x}(A \cos x+B \sin x) \text{ is } \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+2 y=0 . $
(ix) The solution of differential equation $\frac{d y}{d x}=\frac{x+2 y}{x}$ is $x+y=k x^{2}$.
(x) Solution of $\frac{x d y}{d x}=y+x \tan \frac{y}{x}$ is $\sin (\frac{y}{x})=c x$.
(xi) The differential equation of all non-horizontal lines in a plane is $\frac{d^{2} x}{d y^{2}}=0$.
Show Answer
Solution
(i) True
I.F. of the given differential equation
$ \frac{d x}{d y}+P_1 x=Q \text{ is } e^{\int P_1 d y} $
(ii) True
(iii) True
(iv) True
(v) False
Since particular solution of a differential equation has no arbitrary constant.
(vi) False
We know that the order of the differential equation is equal to the number of arbitrary constants.
(vii) True
The given differential equation is
$ \begin{aligned} \frac{d y}{d x} & =(\frac{y}{x})^{1 / 3} \\ \Rightarrow \quad \frac{d y}{d x} & =\frac{y^{1 / 3}}{x^{1 / 3}} \Rightarrow \frac{d y}{y^{1 / 3}}=\frac{d x}{x^{1 / 3}} \end{aligned} $
Integrating both sides, we get
$\int \frac{d y}{y^{1 / 3}} =\int \frac{d x}{x^{1 / 3}} \Rightarrow \int y^{-1 / 3} d y=\int x^{-1 / 3} d x$
$\Rightarrow \frac{1}{-\frac{1}{3}+1} y^{-1 / 3+1} =\frac{1}{-1 / 3+1} \cdot x^{-1 / 3+1}+c$
$\Rightarrow \quad \frac{3}{2} y^{2 / 3} =\frac{3}{2} x^{2 / 3}+c$
$\Rightarrow \quad y^{2 / 3} =x^{2 / 3}+\frac{2}{3} c \Rightarrow y^{2 / 3}-x^{2 / 3}=k[k=\frac{2}{3} c]$
(viii) True
Given equation is
$ y=e^{x}(A \cos x+B \sin x) $
Differentiating both sides, we get
$ \begin{aligned} & \frac{d y}{d x}=e^{x}(-A \sin x+B \cos x)+(A \cos x+B \sin x) e^{x} \\ & \frac{d y}{d x}=e^{x}(-A \sin x+B \cos x)+y \end{aligned} $
Again differentiating w.r.t. $x$, we get
$ \begin{aligned} & \frac{d^{2} y}{d x^{2}}=e^{x}(-A \cos x-B \sin x)+(-A \sin x+B \cos x) \cdot e^{x}+\frac{d y}{d x} \\ & \frac{d^{2} y}{d x^{2}}=-e^{x}(A \cos x+B \sin x)+\frac{d y}{d x}-y+\frac{d y}{d x} \\ & \frac{d^{2} y}{d x^{2}}=-y-y+2 \frac{d y}{d x} \quad \therefore \quad \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+2 y=0 \end{aligned} $
(ix) True
The given differential equation is
$ \begin{aligned} \frac{d y}{d x} & =\frac{x+2 y}{x} \\ \Rightarrow \quad \frac{d y}{d x} & =1+2 \frac{y}{x} \Rightarrow \frac{d y}{d x}-\frac{2 y}{x}=1 \end{aligned} $
Here, $P=\frac{-2}{x}$ and $Q=1$
Integrating factor I.F. $=e^{\int \frac{-2}{x} d x}=e^{-2 \log x}=e^{\log x^{-2}}=\frac{1}{x^{2}}$
$\therefore$ Solution is $y \times$ I.F. $=\int Q \times$ I.F. $d x+c$
$\Rightarrow y \times \frac{1}{x^{2}}=\int 1 \times \frac{1}{x^{2}} d x+c$
$\Rightarrow \quad \frac{y}{x^{2}}=\int \frac{1}{x^{2}} d x+c \Rightarrow \frac{y}{x^{2}}=-\frac{1}{x}+c$
$\Rightarrow \quad y=-x+c x^{2} \Rightarrow y+x=c x^{2}$
(x) True
The given differential equation is
$ \begin{aligned} & x \frac{d y}{d x}=y+x \tan (\frac{y}{x}) \\ & x \frac{d y}{d x}=-x \tan (\frac{y}{x})=y \\ & \Rightarrow \frac{d y}{d x}-\tan (\frac{y}{x})=\frac{y}{x} \Rightarrow \frac{d y}{d x}=\frac{y}{x}+\tan (\frac{y}{x}) \\ & \text{ Put } y=v x \Rightarrow \frac{d y}{d x}=v+x \frac{d v}{d x} \\ & \Rightarrow \quad v+x \cdot \frac{d v}{d x}=\frac{v x}{x}+\tan (\frac{v x}{x}) \end{aligned} $
$ \begin{aligned} & \Rightarrow \quad v+x \frac{d v}{d x}=v+\tan v \Rightarrow x \frac{d v}{d x}=\tan v \\ & \Rightarrow \quad \frac{d v}{\tan v}=\frac{d x}{x} \Rightarrow \cot v d v=\frac{d x}{x} \end{aligned} $
Integrating both sides, we get
$ \begin{matrix} \int \cot v d v =\int \frac{d x}{x} \Rightarrow \log \sin v=\log x+\log c \\ \Rightarrow \quad \log \sin v-\log x =\log c \Rightarrow \log \sin \frac{y}{x}=\log x c \\ \therefore \qquad \sin \frac{y}{x} =x c \end{matrix} $
(xi) True
Let $y=m x+c$ be the non-horizontal line in a plane
$\therefore \qquad \frac{d y}{d x}=m$ and $\frac{d^{2} y}{d x^{2}}=0$.










