SATHEE: Trigonometric Functions

Trigonometric Functions

Short Answer Type Questions

1. Prove that $\frac{\tan A + \sec A - 1}{\tan A - \sec A + 1} = \frac{1 + \sin A}{\cos A}$ .

Show Answer

Thinking Process

Here, use the formulae i.e., $\sec^{2} A - \tan^{2} A = 1$ and $a^{2} - b^{2} = (a + b) (a - b)$ to solve the above problem.

Solution

$\begin{aligned} L H S & = \frac{\tan A + \sec A - 1}{\tan A - \sec A + 1} \\ = \frac{\tan A + \sec A - (\sec^{2} A - \tan^{2} A)}{(\tan A - \sec A + 1)} \\ [∵ \sec^{2} A - \tan^{2} A = 1] \\ = \frac{(\tan A + \sec A) - (\sec A + \tan A) (\sec A - \tan A)}{(1 - \sec A + \tan A)} \\ = \frac{(\sec A + \tan A) (1 - \sec A + \tan A)}{1 - \sec A + \tan A} \\ = \sec A + \tan A = \frac{1}{\cos A} + \frac{\sin A}{\cos A} \\ = \frac{1 + \sin A}{\cos A} = R H S Hence proved. \end{aligned}$

2. If $\frac{2 \sin α}{1 + \cos α + \sin α} = y$ , then prove that $\frac{1 - \cos α + \sin α}{1 + \sin α}$ is also equal to $y$ .

Show Answer

Solution

Given that, $\frac{2 \sin α}{1 + \cos α + \sin α} = y$

$\begin{aligned} Now, & \frac{1 - \cos α + \sin α}{1 + \sin α} \\ = \frac{(1 - \cos α + \sin α)}{(1 + \sin α)} \cdot \frac{(1 + \cos α + \sin α)}{(1 + \cos α + \sin α)} \\ = \frac{(1 + \sin α) - \cos α}{(1 + \sin α)} \cdot \frac{(1 + \sin α) + \cos α}{(1 + \cos α + \sin α)} \\ = \frac{(1 + \sin α)^{2} - \cos^{2} α}{(1 + \sin α) (1 + \sin α + \cos α)} \\ = \frac{(1 + \sin^{2} α + 2 \sin α) - \cos^{2} α}{(1 + \sin α) (1 + \sin α + \cos α)} \end{aligned}$

$\begin{aligned} = \frac{1 + \sin^{2} α + 2 \sin α - 1 + \sin^{2} α}{(1 + \sin α) (1 + \sin α + \cos α)} \\ = \frac{2 \sin^{2} α + 2 \sin α}{(1 + \sin α) (1 + \sin α + \cos α)} \\ = \frac{2 \sin α (1 + \sin α)}{(1 + \sin α) (1 + \sin α + \cos α)} \\ = \frac{2 \sin α}{1 + \sin α + \cos α} = y \end{aligned}$

Hence proved.

3. If $m \sin θ = n \sin (θ + 2 α)$ , then prove that $\tan (θ + α) \cot α = \frac{m + n}{m - n}$ .

Show Answer

Solution

Given that,

$\begin{aligned} Given that, \begin{aligned} m \sin θ & = n \sin (θ + 2 α) \\ ∴ & \frac{\sin (θ + 2 α)}{\sin θ} = \frac{m}{n} \end{aligned} \end{aligned}$

Using componendo and dividendo, we get

$\begin{array}{r} \frac{\sin (θ + 2 α) + \sin θ}{\sin (θ + 2 α) - \sin θ} = \frac{m + n}{m - n} \\ \Rightarrow \frac{2 \sin \frac{θ + 2 α + θ}{2} \cdot \cos \frac{θ + 2 α - θ}{2}}{2 \cos \frac{θ + 2 α + θ}{2} \cdot \sin \frac{θ + 2 α - θ}{2}} = \frac{m + n}{m - n} \\ \Rightarrow [∵ \sin x + \sin y = 2 \sin \frac{x + y}{2} \cdot \cos \frac{x - y}{2} . \\ and . \sin x - \sin y = 2 \cos \frac{x + y}{2} \sin \cdot \frac{x - y}{2}] \\ \Rightarrow \frac{\sin (θ + α) \cdot \cos α}{\cos (θ + α) \cdot \sin α} = \frac{m + n}{m - n} \\ \tan (θ + α) \cdot \cot α = \frac{m + n}{m - n} Hence proved. \end{array}$

4. If $\cos (α + β) = \frac{4}{5}$ and $\sin (α - β) = \frac{5}{13}$ , where $α$ lie between 0 and $\frac{π}{4}$ , then find that value of $\tan 2 α$ .

Show Answer

Solution

Given that,

$\cos (α + β) = \frac{4}{5} and \sin (α - β) = \frac{5}{13}$

$\Rightarrow \sin (α + β) = \sqrt{1 - \frac{16}{25}} = \sqrt{\frac{9}{25}} = \pm \frac{3}{5}$

$∴ \sin (α + β) = \frac{3}{5}$

$and \cos (α - β) = \sqrt{1 - \frac{25}{169}} = \sqrt{\frac{144}{169}} = \pm \frac{12}{13}$

$∴ \cos (α - β) = \frac{12}{13}$

$Now, \tan (α + β) = \frac{\sin (α + β)}{\cos (α + β)}$

$[since, α lies between 0 and \frac{π}{4}]$

$= \frac{\frac{3}{5}}{\frac{4}{5}} = \frac{3}{4}$

$and \tan (α - β) = \frac{\sin (α - β)}{\cos (α - β)} = \frac{\frac{5}{13}}{\frac{12}{13}} = \frac{5}{12}$

$∴ \tan 2 α = \tan (α + β + α - β)$

$= \frac{\tan (α + β) + \tan (α - β)}{1 - \tan (α + β) \cdot \tan (α - β)} [∵ \tan (x \pm y) = \frac{\tan x \pm \tan y}{1 \mp \tan x \cdot \tan y}]$

$= \frac{\frac{3}{4} + \frac{5}{12}}{1 - \frac{3}{4} \cdot \frac{5}{12}} = \frac{\frac{9 + 5}{12}}{\frac{16 - 5}{16}} = \frac{14 \times 16}{12 \times 11} = \frac{56}{33}$

5. If $\tan x = \frac{b}{a}$ , then find the value of $\sqrt{\frac{a + b}{a - b}} + \sqrt{\frac{a - b}{a + b}}$ .

Show Answer

Thinking Process

First of all rationalise the given expression and used the formula, i.e., $\cos 2 x = \cos^{2} x - \sin^{2} x$ .

Solution

Given that, $\tan x = \frac{b}{a}$

$∴ \sqrt{\frac{a + b}{a - b}} + \sqrt{\frac{a - b}{a + b}} = \frac{\sqrt{(a + b)^{2}} + \sqrt{(a - b)^{2}}}{\sqrt{(a - b) (a + b)}}$

$= \frac{(a + b) + (a - b)}{\sqrt{a^{2} - b^{2}}} = \frac{2 a}{\sqrt{a^{2} - b^{2}}} = \frac{2 a}{a \sqrt{1 - \frac{b}{a}}} [∵ \frac{b}{a} = \tan]$

$= \frac{2}{\sqrt{1 - \tan^{2} x}} = \frac{2 \cos x}{\sqrt{\cos^{2} x - \sin^{2} x}} [∵ \cos 2 x = \cos^{2} x - \sin^{2} x] x$

$= \frac{2 \cos x}{\sqrt{\cos 2 x}}$

6. Prove that $\cos θ \cos \frac{θ}{2} - \cos 3 θ \cos \frac{9 θ}{2} = \sin 7 θ \sin 8 θ$ .

Show Answer

Solution

LHS $= \cos θ \cos \frac{θ}{2} - \cos 3 θ \cos \frac{9 θ}{2}$

$\begin{aligned} = \frac{1}{2} 2 \cos θ \cdot \cos \frac{θ}{2} - 2 \cos 3 θ \cdot \cos \frac{9 θ}{2} \\ = \frac{1}{2} \cos θ + \frac{θ}{2} + \cos θ - \frac{θ}{2} - \cos 3 θ + \frac{9 θ}{2} - \cos 3 θ - \frac{9 θ}{2} \\ = \frac{1}{2} (\cos \frac{3 θ}{2} + \cos \frac{θ}{2} - \cos \frac{15 θ}{2} - \cos \frac{3 θ}{2} . \\ = \frac{1}{2} \cos \frac{θ}{2} - \cos \frac{15 θ}{2} \end{aligned}$

$= - \frac{1}{2} 2 \sin \frac{θ + 15 θ}{2} \cdot \sin \frac{θ - 15 θ}{2}$

$[∵ \cos x - \cos y = - 2 \sin \frac{x + y}{2} \cdot \sin \frac{x - y}{2}]$

$= + (\sin 8 θ \cdot \sin 7 θ) = R H S$

$∴ LHS = RHS$

Hence Proved

7. If $a \cos θ + b \sin θ = m$ and $a \sin θ - b \cos θ = n$ , then show that $a^{2} + b^{2} = m^{2} + n^{2}$ .

Show Answer

Solution

Given that,

and

$a \cos θ + b \sin θ = m . . (i)$

$a \sin θ - b \cos θ = n . . (i i)$

On squaring and adding of Eqs. (i) and (ii), we get

$m^{2} + n^{2} = (a \cos θ + b \sin θ)^{2} + (a \sin θ - b \cos θ)^{2}$

$= a^{2} \cos^{2} θ + b^{2} \sin^{2} θ + 2 a b \sin θ \cdot \cos θ + a^{2} \sin^{2} θ + b^{2} \cos^{2} θ$

$\Rightarrow m^{2} + n^{2} = a^{2} (\cos^{2} θ + \sin^{2} θ) + b^{2} (\sin^{2} θ + \cos^{2} θ) - 2 a b \sin θ \cdot \cos θ$

$\Rightarrow m^{2} + n^{2} = a^{2} + b^{2} Hence proved.$

8. Find the value of $\tan 22^{\circ} 30^{'}$ .

Show Answer

Solution

Let

$Let θ = 45^{\circ}$

$We know that, \tan \frac{θ}{2} = \frac{\sin \frac{θ}{2}}{\cos \frac{θ}{2}} = \frac{2 \sin \frac{θ}{2} \cdot \cos \frac{θ}{2}}{2 \cos^{2} \frac{θ}{2}} \Rightarrow \tan \frac{θ}{2} = \frac{\sin θ}{1 + \cos θ}$

$∴ \tan 22^{\circ} 30^{'} = \frac{\sin 45^{\circ}}{1 + \cos 45^{\circ}} [∵ θ = 45^{\circ}]$

$= \frac{\frac{1}{\sqrt{2}}}{1 + \frac{1}{\sqrt{2}}} = \frac{1}{\sqrt{2} + 1}$

9. Prove that $\sin 4 A = 4 \sin A \cos^{3} A - 4 \cos A \sin^{3} A$ .

Show Answer

Thinking Process

Here, apply the formula i.e., $\sin 2 x = 2 \sin x \cos x$ and $\cos 2 x = \cos^{2} x - \sin^{2} x$

Solution

$L H S = \sin 4 A$

$= 2 \sin 2 A \cdot \cos 2 A$

$= 2 (2 \sin A \cdot \cos A) (\cos^{2} A - \sin^{2} A)$

$= 4 \sin A \cdot \cos^{3} A - 4 \cos A \sin^{3} A$

$[∵ \cos 2 A = \cos^{2} A - \sin^{2} A and \sin 2 A = 2 \sin A \cdot \cos A]$

$∴ L H S = R H S Hence Proved$

10. If $\tan θ + \sin θ = m$ and $\tan θ - \sin θ = n$ , then prove that $m^{2} - n^{2} = 4 \sin θ \tan θ$ .

Show Answer

Solution

Now,

Also, Given that,

$\tan θ + \sin θ = m . . (i)$

$and \tan θ - \sin θ = n . . (i i)$

$Now m + n = \tan θ + \sin θ + \tan θ - \sin θ$

$m + n = 2 \tan θ \dots (i i i)$

$also m - n = \tan θ + \sin θ - \tan θ + \sin θ$

$m - n = 2 \sin θ \dots (i v)$

From Eqs. (iii) and (iv),

$\begin{aligned} (m + n) (m - n) & = 4 \sin θ \cdot \tan θ \\ m^{2} - n^{2} & = 4 \sin θ \cdot \tan θ Hence Proved \end{aligned}$

11. If $\tan (A + B) = p$ and $\tan (A - B) = q$ , then show that $\tan 2 A = \frac{p + q}{1 - p q}$ .

Show Answer

Solution

Given that $\tan (A + B) = p . . (i)$

and $\tan (A - B) = q . . (i i)$

$∴ \tan 2 A = \tan (A + B + A - B)$

$= \frac{\tan (A + B) + \tan (A - B)}{1 - \tan (A + B) \tan (A - B)} [∵ \tan (x + y) = \frac{\tan x + \tan y}{1 - \tan x \tan y}]$

$= \frac{p + q}{1 - p q}$ [from Eqs. (i) and (ii)]

12. If $\cos α + \cos β = 0 = \sin α + \sin β$ , then prove that $\cos 2 α + \cos 2 β = - 2 \cos (α + β)$ .

Show Answer

Solution

Given that, $\cos α + \cos β = 0 = \sin α + \sin β$

$\Rightarrow (\cos α + \cos β)^{2} - (\sin α + \sin β)^{2} = 0$

$\Rightarrow \cos^{2} α + \cos^{2} β + 2 \cos α \cos β - \sin^{2} α - \sin^{2} β - 2 \sin α \sin β = 0$

$\Rightarrow \cos^{2} α - \sin^{2} α + \cos^{2} β - \sin^{2} β = 2 (\sin α \sin β - \cos α \cos β)$

$\Rightarrow \cos 2 α + \cos 2 β = - 2 \cos (α + β)$

Hence proved.

13. If $\frac{\sin (x + y)}{\sin (x - y)} = \frac{a + b}{a - b}$ , then show that $\frac{\tan x}{\tan y} = \frac{a}{b}$ .

Show Answer

Solution

Given that, $\frac{\sin (x + y)}{\sin (x - y)} = \frac{a + b}{a - b}$

Using componendo and dividendo,

$\Rightarrow= \frac{\sin (x + y) + [\sin (x - y)]}{\sin (x + y) - \sin (x - y)} = \frac{a + b + a - b}{a + b - a + b}$

$\Rightarrow= \frac{2 \sin \frac{x + y + x - y}{2} \cdot \cos \frac{x + y - x + y}{2}}{2 \cos \frac{x + y + x - y}{2} \cdot \sin \frac{x + y - x + y}{2}} = \frac{2 a}{2 b}$

$[∵ \sin x + \sin y = 2 \sin \frac{x + y}{2} \cdot \cos \frac{x - y}{2} and \sin x - \sin y = 2 \cos \frac{x + y}{2} \cdot \sin \frac{x - y}{2}]$

$\Rightarrow= \frac{\sin x \cdot \cos y}{\cos x \cdot \sin y} = \frac{a}{b}$

$\frac{\tan x}{\tan y} = \frac{a}{b}$

14. If $\tan θ = \frac{\sin α - \cos α}{\sin α + \cos α}$ , then show that $\sin α + \cos α = \sqrt{2} \cos θ$ .

Show Answer

Solution

Given that, $\tan θ = \frac{\sin α - \cos α}{\sin α + \cos α}$

$\begin{matrix} \Rightarrow \tan θ = \frac{\cos α (\tan α - 1)}{\cos α (\tan α + 1)} \\ \Rightarrow \tan θ = \frac{\tan α - \tan \frac{π}{4}}{1 + \tan \frac{π}{4} \cdot \tan α} & [∵ \tan \frac{π}{4} = 1] \end{matrix}$

Trigonometric Functions

$\Rightarrow \tan θ = \tan (α - \frac{π}{4})$

$\Rightarrow θ = α - \frac{π}{4} \Rightarrow α = θ + \frac{π}{4}$

$∴ \sin α + \cos α = \sin (θ + \frac{π}{4}) + \cos (θ + \frac{π}{4})$

$= \sin θ \cdot \cos \frac{π}{4} + \cos θ \cdot \sin \frac{π}{4} + \cos θ \cdot \cos \frac{π}{4} - \sin θ \cdot \sin \frac{π}{4}$

$= \frac{1}{\sqrt{2}} \sin θ + \frac{1}{\sqrt{2}} \cos θ + \frac{1}{\sqrt{2}} \cos θ - \frac{1}{\sqrt{2}} \sin θ [∵ \sin \frac{π}{4} = \cos \frac{π}{4} = \frac{1}{\sqrt{2}}]$

$= \frac{2}{\sqrt{2}} \cdot \cos θ = \sqrt{2} \cos θ$

15. If $\sin θ + \cos θ = 1$ , then find the general value of $θ$ .

Show Answer

Thinking Process

If $\sin θ = \sin α$ , then $θ = n π + (- 1)^{n} \cdot α$ , gives general solution of the given equation.

Solution

Given that, $\sin θ + \cos θ = 1$

On squaring both sides, we get

$\sin^{2} θ + \cos^{2} θ + 2 \sin θ \cdot \cos θ = 1$

$\Rightarrow 1 + 2 \sin θ \cdot \cos = 1 [∵ \sin 2 x = 2 \sin x \cos x]$

$\Rightarrow \sin 2 θ = 02 θ = n π + (- 1)^{n} \cdot 0$

$∴ θ = \frac{n π}{2}$

Alternate Method

$\sin θ + \cos θ = 1$

$\Rightarrow \frac{1}{\sqrt{2}} \cdot \sin θ + \frac{1}{\sqrt{2}} \cdot \cos θ = \frac{1}{\sqrt{2}}$

$\Rightarrow \sin θ \cdot \cos \frac{π}{4} + \cos θ \cdot \sin \frac{π}{4} = \frac{1}{\sqrt{2}} ∵ \sin \frac{π}{4} = \frac{1}{\sqrt{2}} = \cos \frac{π}{4}$

$\Rightarrow \sin θ + \frac{π}{4} = \sin \frac{π}{4} [∵ \sin (x + y) = \sin x \cdot \cos y + \cos x \cdot \sin y]$

$\Rightarrow θ + \frac{π}{4} = n π + (- 1)^{n} \frac{π}{4}$

$∴ θ = n π + (- 1)^{n} \frac{4}{4} - \frac{π}{4}$

16. Find the most general value of $θ$ satisfying the equation $\tan θ = - 1$ and $\cos θ = \frac{1}{\sqrt{2}}$ .

Show Answer

Solution

The given equations are

$\tan θ = - 1 . . (i)$

$and \cos θ = \frac{1}{\sqrt{2}} . . (i i)$

$From Eq. (i), \tan θ = - \tan \frac{π}{4}$

$\Rightarrow \tan θ = \tan (2 π - \frac{π}{4}) \Rightarrow \tan θ = \tan \frac{7 π}{4}$

$∴ θ = \frac{7 π}{4}$

From Eq. (ii),

$\Rightarrow \cos θ = \cos (2 π - \frac{π}{4}) \Rightarrow \cos θ = \cos \frac{7 π}{4}$

$∴ θ = \frac{7 π}{4}$

Hence, the most general value of $θ$ i.e., $θ = 2 n π + \frac{7 π}{4}$ .

17. If $\cot θ + \tan θ = 2 c o s e c θ$ , then find the general value of $θ$ .

Show Answer

Solution

Given that,

$\cot θ + \tan θ = 2 c o s e c θ$

$\frac{\cos θ}{\sin θ} + \frac{\sin θ}{\cos θ} = \frac{2}{\sin θ}$

$\Rightarrow \frac{\cos^{2} + \sin^{2} θ}{\sin θ \cdot \cos θ} = \frac{2}{\sin θ}$

$\Rightarrow \frac{1}{\cos θ} = 2 [∵ \sin^{2} θ + \cos^{2} θ = 1]$

$\Rightarrow \cos θ = \frac{1}{2} \Rightarrow \cos θ = \cos \frac{π}{3}$

$∴ θ = 2 n π \pm \frac{π}{3}$

18. If $2 \sin^{2} θ = 3 \cos θ$ , where $0 \leq θ \leq 2 π$ , then find the value of $θ$ .

Show Answer

Solution

Given that,

$Given that , 2 \sin^{2} θ = 3 \cos θ$

$\Rightarrow 2 - 2 \cos^{2} θ = 3 \cos θ$

$\Rightarrow 2 \cos^{2} θ + 3 \cos θ - = 0$

$\Rightarrow 2 \cos^{2} θ + 4 \cos θ - \cos θ - 2 = 0$

$\Rightarrow 2 \cos θ (\cos θ + 2) - 1 (\cos θ + 2) = 0$

$\Rightarrow (\cos θ + 2) (2 \cos θ - 1) = 0$

$\Rightarrow \cos θ = - 2 n o t p o s s i b l e [∵ - 1 \leq \cos θ \leq 1]$

$\Rightarrow 2 \cos θ = 1$

$\Rightarrow \cos θ = \frac{1}{2}$

$\Rightarrow \cos θ = \cos \frac{π}{3}$

$∴ θ = \frac{π}{3}$

$A l s o, \cos θ = \cos (2 π - \frac{π}{3})$

$\Rightarrow \cos θ = \cos \frac{5 π}{6}$

$∴ θ = \frac{5 π}{6}$

So, the values of $θ$ are $\frac{π}{3}$ and $\frac{5 π}{6}$ .

19. If $\sec x \cos 5 x + 1 = 0$ , where $0 < x \leq \frac{π}{2}$ , then find the value of $x$ .

Show Answer

Solution

Given that, $\sec x \cos 5 x + 1 = 0$

$\frac{\cos 5 x}{\cos x} + 1 = 0 \Rightarrow \cos 5 x + \cos x = 0$

$\Rightarrow 2 \cos (\frac{5 x + x}{2}) \cdot \cos (\frac{5 x - x}{2}) = 0$

$[∵ \cos x + \cos y = 2 \cos \frac{x + y}{2} \cdot \cos \frac{x - y}{2}]$

$\Rightarrow 2 \cos 3 x \cdot \cos 2 x = 0$

$\Rightarrow \cos 3 x = 0 or \cos 2 x = 0$

$\Rightarrow \cos 3 x = \cos \frac{π}{2} or \cos 2 x = \cos \frac{π}{2}$

$∴ 3 x = \frac{π}{2} \Rightarrow 2 x = \frac{π}{2}$

$x = \frac{π}{6} \Rightarrow x = \frac{π}{4}$

Hence, the solutions are $\frac{π}{2}, \frac{π}{4}$ and $\frac{π}{6}$ .

Long Answer Type Questions

20. If $\sin (θ + α) = a$ and $\sin (θ + β) = b$ , then prove that $\cos (α + β) - 4 a b \cos (α - β) = 1 - 2 a^{2} - 2 b^{2}$ .

$∵$ Thinking Process

Express $\cos (α - β) = \cos (θ + α) - (θ + β)$

Show Answer

Solution

Given that, $\sin (θ + α) = a . . (i)$

and

$\sin (θ + β) = b . . (i i)$

$∴ \cos (θ + α) = \sqrt{1 - a^{2}}$ and $\cos (θ + β) = \sqrt{1 - b^{2}}$

$∴ \cos (α - β) = \cos θ + α - (θ + β)$

$= \cos (θ + β) \cos (θ + α) + \sin (θ + α) \sin (θ + β)$

$\begin{aligned} = \sqrt{1 - a^{2}} \sqrt{1 - b^{2}} + a \cdot b = a b + \sqrt{(1 - a^{2}) (1 - b^{2})} \\ = a b + \sqrt{1 - a^{2} - b^{2} + a^{2} b^{2}} \end{aligned}$

and

$\cos (α - β) = a b + \sqrt{1 - a^{2} - b^{2} + a^{2} b^{2}}$

$= \cos 2 (α - β) - 4 a b \cos (α - β)$

$= 2 \cos^{2} (α - β) - 1 - 4 a b \cos (α - β)$

$= 2 \cos (α - β) (\cos α - β - 2 a b) - 1$

$= 2 (a b + \sqrt{1 - a^{2} - b^{2} + a^{2} b^{2}}) (a b + \sqrt{1 - a^{2} - b^{2} + a^{2} b^{2}} - 2 a b) - 1$

$= 2 [(\sqrt{1 - a^{2} - b^{2} + a^{2} b^{2} + a b}) (\sqrt{1 - a^{2} - b^{2} + a^{2} b^{2}} - a b)] - 1$

$= 2 [1 - a^{2} - b^{2} + a^{2} b^{2} - a^{2} b^{2}] - 1$

$= 2 - 2 a^{2} - 2 b^{2} - 1$

$= 1 - 2 a^{2} - 2 b^{2} H e n c e P r o v e d$

21. If $\cos (θ + φ) = m \cos (θ - φ)$ , then prove that $\tan θ = \frac{1 - m}{1 + m} \cot φ$ .

Show Answer

Solution

Given that,

$\begin{aligned} \cos (θ + φ) = m \cos (θ - φ) \\ \Rightarrow \frac{\cos (θ + φ)}{\cos (θ - φ)} = \frac{m}{1} \end{aligned}$

Using componendo and dividendo rule,

$\frac{\cos (θ - φ) - \cos (θ + φ)}{\cos (θ - φ) + \cos (θ + φ)} = \frac{1 - m}{1 + m}$

$\Rightarrow \frac{- 2 \sin \frac{θ - φ + θ + φ}{2} \cdot \sin \frac{θ - φ - θ - φ}{2}}{2 \cos \frac{θ - φ + θ + φ}{2} \cdot \cos \frac{θ - φ - θ - φ}{2}} = \frac{1 - m}{1 + m}$

$\Rightarrow \frac{\sin θ \cdot \sin φ}{\cos θ \cdot \cos φ} = \frac{1 - m}{1 + m} [∵ \sin (- θ) = - \sin θ a n d \cos (- θ) = \cos θ]$

$\Rightarrow \tan θ \cdot \tan φ = \frac{1 - m}{1 + m}$

$\Rightarrow \tan θ = \frac{1 - m}{1 + m} \cot φ$

22. Find the value of the expression

$3 [\sin^{4} \frac{3 π}{2} - α + \sin^{4} (3 π + α)] - 2 [\sin^{6} (\frac{π}{2} + α) + \sin^{6} (5 π - α)] .$

Show Answer

Solution

Given expression,

$\begin{aligned} 3 [\sin^{4} & (\frac{3 π}{2}) - α + \sin^{4} (3 π + α)] - 2 [\sin^{6} \frac{π}{2} + α + \sin^{6} (5 π - α)] \\ = 3 [\cos^{4} α + \sin^{4} (π + α)] - 2 [\cos^{6} α + \sin^{6} (π - α)] \\ = 3 [\cos^{4} α + \sin^{4} α] - 2 [\cos^{6} α + \sin^{6} α] = 3 - 2 = 1 \end{aligned}$

23. If $a \cos 2 θ + b \sin 2 θ = c$ has $α$ and $β$ as its roots, then prove that $\tan α + \tan β = \frac{2 b}{a + c}$ .

Show Answer

Solution

Given that, $a \cos 2 θ + b \sin 2 θ = c$

$\Rightarrow a \frac{1 - \tan^{2} θ}{1 + \tan^{2} θ} + b \frac{2 \tan θ}{1 + \tan^{2} θ} = c$

$[∵ \sin 2 θ = \frac{2 \tan θ}{1 + \tan^{2} θ} and \cos 2 θ = \frac{1 - \tan^{2} θ}{1 + \tan^{2} θ}]$

$\Rightarrow a (1 - \tan^{2} θ) + 2 b \tan θ = c (1 + \tan^{2} θ)$

$\Rightarrow a - a - \tan^{2} θ + 2 b \tan θ = c + c \tan^{2} θ$

$\Rightarrow (a + c) \tan^{2} θ - 2 b \tan θ + c - a = 0$

Since, this equation has $\tan α$ and $\tan β$ as its roots.

$∵ \tan α + \tan β = \frac{- (- 2 b)}{a + c} = \frac{2 b}{a + c}$

24. If $x = \sec φ - \tan φ$ and $y = c o s e c φ + \cot φ$ , then show that $x y + x - y + 1 = 0$ .

Show Answer

Solution

Given that, and $x = \sec φ - \tan φ . . (i)$

Now,

$y = c o s e c φ + \cot φ . . (i i)$

$\Rightarrow x y = \sec φ \cdot c o s e c φ - c o s e c φ \cdot \tan φ + \sec φ \cdot \cot φ - \tan φ \cdot \cot φ$

$\Rightarrow x y = \sec φ \cdot c o s e c φ - \frac{1}{\cos φ} + \frac{1}{\sin φ} - 1$

$\Rightarrow 1 + x y = \sec φ c o s e c φ - \sec φ + c o s e c φ . . (i i i)$

From Eqs. (i) and (ii), we get

$x - y = \sec φ - \tan φ - c o s e c φ - \cot φ$

$\Rightarrow x - y = \sec φ - c o s e c φ - \frac{\sin φ}{\cos φ} - \frac{\cos φ}{\sin φ}$

$\Rightarrow x - y = \sec φ - c o s e c φ - (\frac{\sin^{2} φ + \cos^{2} φ}{\sin φ \cdot \cos φ})$

$\Rightarrow x - y = \sec φ - c o s e c φ - \frac{1}{\sin φ \cdot \cos φ}$

$\begin{aligned} \Rightarrow x - y = \sec φ - c o s e c φ - c o s e c φ \cdot \sec φ \\ \Rightarrow x - y = - (\sec φ \cdot c o s e c φ - \sec φ + c o s e c φ) \\ \Rightarrow x - y = - (x y + 1) \\ \Rightarrow x y + x - y + 1 = 0 [from Eq. (iii)] Hence proved. \end{aligned}$

25. If $θ$ lies in the first quadrant and $\cos θ = \frac{8}{17}$ , then find the value of $\cos (30^{\circ} + θ) + \cos (45^{\circ} - θ) + \cos (120^{\circ} - θ)$ .

Show Answer

Solution

Given that,

$\Rightarrow \sin θ = \sqrt{\frac{289 - 64}{289}}$

$\Rightarrow \sin θ = \pm \frac{15}{17}$

$\Rightarrow \sin θ = \frac{15}{17} [Since, θ lies in first quadrant]$

$Now, \cos (30^{\circ} + θ) + \cos (45^{\circ} - θ) + \cos (120^{\circ} - θ)$

$= \cos (30^{\circ} + θ) + \cos (45^{\circ} - θ) + \cos (90^{\circ} + 30^{\circ} - θ)$

$= \cos (30^{\circ} + θ) + \cos (45^{\circ} - θ) - \sin (30^{\circ} - θ)$

$= \cos 30^{\circ} \cos θ - \sin 30^{\circ} \sin θ + \cos 45^{\circ} \cos θ + \sin 45^{\circ} \sin θ$

$= \frac{\sqrt{3}}{2} \cos θ - \frac{1}{2} \sin θ + \frac{1}{\sqrt{2}} \cos θ + \frac{1}{\sqrt{2}} \sin θ - \frac{1}{2} \cos θ \frac{\sqrt{3}}{2} \sin θ$

$= \frac{\sqrt{3}}{2} + \frac{1}{\sqrt{2}} - \frac{1}{2} \cos θ + \frac{1}{\sqrt{2}} - \frac{1}{2} + \frac{\sqrt{3}}{2} \sin θ$

$= \frac{\sqrt{6} + 2 - \sqrt{2}}{2 \sqrt{2}} \cos θ + \frac{2 - \sqrt{2} + \sqrt{6}}{2 \sqrt{2}} \sin θ$

$= \frac{\sqrt{6} + 2 - \sqrt{2}}{2 \sqrt{2}} \frac{8}{17} + \frac{2 - \sqrt{2} + \sqrt{6}}{2 \sqrt{2}} \frac{15}{17}$

$\begin{aligned} = \frac{1}{17 (2 \sqrt{2})} (8 \sqrt{6} + 16 - 8 \sqrt{2} + 30 - 15 \sqrt{2} + 15 \sqrt{6}) \\ = \frac{1}{17 (2 \sqrt{2})} (23 \sqrt{6} - 23 \sqrt{2} + 46) \\ = \frac{23 \sqrt{6}}{17 (2 \sqrt{2})} - \frac{23 \sqrt{2}}{17 (2 \sqrt{2})} + \frac{46}{17 (2 \sqrt{2})} \\ = \frac{23 \sqrt{3}}{17 (2)} - \frac{23}{17 (2)} + \frac{23}{17 \sqrt{2}} \\ = \frac{23}{17} \frac{\sqrt{3} - 1}{2} + \frac{1}{\sqrt{2}} \end{aligned}$

26. Find the value of $\cos^{4} \frac{π}{8} + \cos^{4} \frac{3 π}{8} + \cos^{4} \frac{5 π}{8} + \cos^{4} \frac{7 π}{8}$ .

Show Answer

Solution

Given expression, $\cos^{4} \frac{π}{8} + \cos^{4} \frac{3 π}{8} + \cos^{4} \frac{5 π}{8} + \cos^{4} \frac{7 π}{8}$

$\begin{aligned} = \cos^{4} \frac{π}{8} + \cos^{4} \frac{3 π}{8} + \cos^{4} π - \frac{3 π}{8} + \cos^{4} π - \frac{π}{8} \\ = \cos^{4} \frac{π}{8} + \cos^{4} \frac{3 π}{8} + \cos^{4} (\frac{3 π}{8}) + \cos^{4} (\frac{π}{8}) \\ = 2 [\cos^{4} \frac{π}{8} + \cos^{4} \frac{3 π}{8}] = 2 [\cos^{4} \frac{π}{8} + \cos^{4} (\frac{π}{2} - \frac{π}{8})] \\ = 2 [\cos^{4} \frac{π}{8} + \sin^{4} \frac{π}{8}] \\ = 2 [\cos^{2} \frac{π}{8} + \sin^{2} \frac{π^{2}}{8} - 2 \cos^{2} \frac{π}{8} \cdot \sin^{2} \frac{π}{8}] \\ = 21 - 2 \cos^{2} \frac{π}{8} \cdot \sin^{2} \frac{π}{8} = 2 - 2 \sin \frac{π}{8} \cdot \cos \frac{π^{2}}{8} \\ = 2 - \sin (\frac{2 π}{8})^{2} = 2 - (\frac{1}{\sqrt{2}}) \\ = 2 - \frac{1}{2} = \frac{3}{2} \end{aligned}$

27. Find the general solution of the equation $5 \cos^{2} θ + 7 \sin^{2} θ - 6 = 0$ .

Show Answer

Solution

Given equation,

$\begin{matrix} \Rightarrow 5 \cos^{2} θ + 7 \sin^{2} θ - 6 & = 0 \\ \Rightarrow 5 \cos^{2} + 7 (1 - \cos^{2} θ) - 6 & = 0 \\ \Rightarrow 5 \cos^{2} θ + 7 - 7 \cos^{2} θ - 6 & = 0 \\ \Rightarrow 5 \cos^{2} θ + 7 - 7 \cos^{2} θ - 6 & = 0 \Rightarrow & \Rightarrow - 2 \cos^{2} θ + 1 = 0 \\ \Rightarrow 2 \cos^{2} θ - 1 = 0 & [∵ \cos^{2} θ = \cos^{2} α] \\ \Rightarrow \cos^{2} θ = \frac{1}{2} & ∴ θ = n π \pm α \\ \Rightarrow \cos^{2} θ & = \cos^{2} \frac{π}{4} \\ θ & = n π \pm \frac{π}{4} \end{matrix}$

28. Find the general of the equation $\sin x - 3 \sin 2 x + \sin 3 x$ $= \cos x - 3 \cos 2 x + \cos 3 x$ .

Show Answer

Solution

Given equation, $\sin x - 3 \sin 2 x + \sin 3 x = \cos x - 3 \cos 2 x + \cos 3 x$

$\begin{aligned} \Rightarrow 2 \sin (\frac{x + 3 x}{2}) \cdot \cos (\frac{3 x - x}{2}) - 3 \sin 2 x \\ = 2 \cos (\frac{3 x + x}{2}) \cdot \cos (\frac{3 x - x}{2}) - 3 \cos 2 x \\ \Rightarrow 2 \sin 2 x \cos x - 3 \sin 2 x = 2 \cos 2 x \cdot \cos x - 3 \cos 2 x \\ \Rightarrow \sin 2 x (2 \cos x - 3) = \cos 2 x (2 \cos x - 3) \\ \Rightarrow \frac{\sin 2 x}{\cos 2 x} = 1 \\ \begin{array}{c} \Rightarrow & \tan 2 x = 1 \end{array} \\ \Rightarrow \tan 2 x = \tan \frac{π}{4} \\ \Rightarrow 2 x = n π + \frac{π}{4} \\ ∴ x = \frac{n π}{2} + \frac{4}{8} \end{aligned}$

29. Find the general solution of the equation

Show Answer

Solution

Given equation is,

$(\sqrt{3} - 1) \cos θ + (\sqrt{3} + 1) \sin θ = 2 . . (i)$

$\begin{aligned} Put \sqrt{3} - 1 = r \sin α and \sqrt{3} + 1 = r \cos α \\ ∴ r^{2} = (\sqrt{3} - 1)^{2} + (\sqrt{3} + 1)^{2} \\ \Rightarrow = 3 + 1 - 2 \sqrt{3} + 3 + 1 + 2 \sqrt{3} \\ \Rightarrow r^{2} = 8 \\ ∴ r = 2 \sqrt{2} \\ now, \tan α = \frac{\sqrt{3} - 1}{\sqrt{3} + 1} = \frac{\tan \frac{π}{3} - \tan \frac{π}{4}}{1 + \tan \frac{π}{3} \cdot \frac{π}{4}} \\ \Rightarrow \tan α = \tan \frac{π}{3} - \frac{π}{4} \\ \Rightarrow \tan α = \tan \frac{π}{12} \\ ∴ α = \frac{π}{12} \end{aligned}$

From Eq. (i), $r \sin α \cos θ + r \cos α \sin θ = 2$

$\begin{matrix} \Rightarrow & r [\sin (θ + α)] = 2 \\ \sin (θ + α) = \frac{2}{2 \sqrt{2}} \\ \Rightarrow & \sin (θ + α) = \frac{1}{\sqrt{2}} \\ \Rightarrow & \sin (θ + α) = \sin \frac{π}{4} θ + α = n π + (- 1)^{n} \frac{π}{4} \\ θ = n π + (- 1)^{n} \cdot \frac{π}{4} - \frac{π}{12} \end{matrix}$

Alternate Method

$\begin{aligned} (\sqrt{3} - 1) \cos θ + (\sqrt{3} + 1) \sin θ & = 2 \\ Put \sqrt{3} - 1 & = r \cos α and \sqrt{3} + 1 = r \sin α \\ ∴ r & = 2 \sqrt{2} \end{aligned}$

Now, $\tan α = \frac{\sqrt{3} + 1}{\sqrt{3} - 1} = \frac{1 + \frac{1}{\sqrt{3}}}{1 - \frac{1}{\sqrt{3}}}$

$\begin{aligned} \Rightarrow \tan α = \frac{\tan \frac{π}{4} + \tan \frac{π}{6}}{1 - \tan \frac{π}{4} \cdot \tan \frac{π}{6}} \\ \Rightarrow \tan α = \tan \frac{π}{4} + \frac{π}{6} \Rightarrow \tan α = \tan \frac{5 π}{12} \end{aligned}$

$α = \frac{5 π}{12}$

From Eq. (i), $r \cos α \cos θ + r \sin α \sin θ = 2$

$r [\cos (θ - α)]$

$\Rightarrow \cos (θ - α) = \frac{2}{2 \sqrt{2}}$

$\Rightarrow \cos (θ - α) = \frac{1}{\sqrt{2}}$

$\Rightarrow \cos (θ - α) = \cos \frac{π}{4}$

$\Rightarrow θ - α = 2 n π \pm \frac{π}{4}$

$∴ θ = 2 n π \pm \frac{π}{4} + \frac{5 π}{12}$

Objective Type Questions

30. If $\sin θ + c o s e c θ = 2$ , then $\sin^{2} θ + c o s e c^{2} θ$ is equal to

(a) 1

(b) 4

(d) None of these

Show Answer

Solution

$\Rightarrow \sin^{2} θ + c o s e c^{2} θ + 2 \sin θ \cdot c o s e c θ = 4$

$\Rightarrow \sin^{2} θ + c o s e c^{2} θ = 4 - 2$

$\Rightarrow \sin^{2} θ + c o s e c^{2} θ = 2$

Option (a) 1: This option is incorrect because if (\sin \theta + \cosec \theta = 2), then (\sin^2 \theta + \cosec^2 \theta) cannot be 1. The given equation leads to (\sin^2 \theta + \cosec^2 \theta = 2), not 1.
Option (b) 4: This option is incorrect because the given equation (\sin \theta + \cosec \theta = 2) simplifies to (\sin^2 \theta + \cosec^2 \theta = 2), not 4.
Option (d) None of these: This option is incorrect because the correct answer is provided in option (c), which is 2. Therefore, “None of these” is not applicable.

31. If $f (x) = \cos^{2} x + \sec^{2} x$ , then

(a) $f (x) < 1$

(b) $f (x) = 1$

(d) $f (x) \geq 2$

Show Answer

Solution

(d) Given that, $f (x) = \cos^{2} x + \sec^{2} x$

We know that, $A M \geq G M$

$\frac{\cos^{2} x + \sec^{2} x}{2} \geq \sqrt{\cos^{2} x \cdot \sec^{2} x}$

$\Rightarrow$

$\cos^{2} x + \sec^{2} x \geq 2$

$[∵ \cos x \cdot \sec x = 1]$

$\Rightarrow f (x) \geq 2$

(a) $f (x) < 1$ : This option is incorrect because $\cos^{2} x$ and $\sec^{2} x$ are both non-negative and $\sec^{2} x$ is always greater than or equal to 1. Therefore, their sum cannot be less than 1.
(b) $f (x) = 1$ : This option is incorrect because $\sec^{2} x$ is always greater than or equal to 1, and $\cos^{2} x$ is always less than or equal to 1. The sum $\cos^{2} x + \sec^{2} x$ cannot equal 1 since $\sec^{2} x$ alone is at least 1.
(c) $2 < f (x) < 1$ : This option is incorrect because it is logically inconsistent. A value cannot be both greater than 2 and less than 1 simultaneously. Additionally, as shown in the solution, $f (x) \geq 2$ .

32. If $\tan θ = \frac{1}{2}$ and $\tan φ = \frac{1}{3}$ , then the value of $θ + φ$ is

(a) $\frac{π}{6}$

(b) $π$

(d) $\frac{π}{4}$

Show Answer

Solution

(d) Given that,

$\begin{matrix} Now, & \tan (θ + φ) = \frac{\tan θ + \tan φ}{1 - \tan θ \cdot \tan φ} \\ \Rightarrow & \tan (θ + φ) = \frac{\frac{1}{2} + \frac{1}{3}}{1 - \frac{1}{2} \cdot \frac{1}{3}} \Rightarrow \tan (θ + φ) = \frac{\frac{3 + 2}{\frac{6}{6}}}{\frac{6 - 1}{6}} = \frac{5}{5} = 1 \\ \Rightarrow & \tan (θ + φ) = \tan \frac{π}{4} \\ ∴ & θ + φ = \frac{π}{4} \end{matrix}$

Option (a) $\frac{π}{6}$ : This option is incorrect because if $θ + φ = \frac{π}{6}$ , then $\tan (θ + φ) = \tan \frac{π}{6} = \frac{1}{\sqrt{3}}$ . However, from the given values of $\tan θ = \frac{1}{2}$ and $\tan φ = \frac{1}{3}$ , we calculated $\tan (θ + φ) = 1$ , which does not match $\frac{1}{\sqrt{3}}$ .
Option (b) $π$ : This option is incorrect because if $θ + φ = π$ , then $\tan (θ + φ) = \tan π = 0$ . However, from the given values of $\tan θ = \frac{1}{2}$ and $\tan φ = \frac{1}{3}$ , we calculated $\tan (θ + φ) = 1$ , which does not match 0.
Option (c) 0: This option is incorrect because if $θ + φ = 0$ , then $\tan (θ + φ) = \tan 0 = 0$ . However, from the given values of $\tan θ = \frac{1}{2}$ and $\tan φ = \frac{1}{3}$ , we calculated $\tan (θ + φ) = 1$ , which does not match 0.

33. Which of the following is not correct?

(a) $\sin θ = - \frac{1}{5}$

(b) $\cos θ = 1$

(d) $\tan θ = 20$

Show Answer

Solution

Hence, $\sec θ$ cannot be equal to $\frac{1}{2}$ .

(a) $\sin θ = - \frac{1}{5}$ : This is incorrect because the range of $\sin θ$ is $[- 1, 1]$ , and $- \frac{1}{5}$ falls within this range. Therefore, this option is actually correct.
(b) $\cos θ = 1$ : This is incorrect because the range of $\cos θ$ is $[- 1, 1]$ , and $1$ falls within this range. Therefore, this option is actually correct.
(d) $\tan θ = 20$ : This is incorrect because the range of $\tan θ$ is all real numbers, so $20$ is a valid value for $\tan θ$ . Therefore, this option is actually correct.

34. The value of $\tan 1^{\circ} \tan 2^{\circ} \tan 3^{\circ} \dots \tan 89^{\circ}$ is

(a) 0

(b) 1

(d) Not defined

Show Answer

Solution

(b) Given expression, $\tan 1^{\circ} \tan 2^{\circ} \tan 3^{\circ} \dots \tan 89^{\circ}$

$\begin{aligned} = \tan 1^{\circ} \tan 2^{\circ} \dots \tan 45^{\circ} \cdot \tan (90^{\circ} - 44^{\circ}) \tan (90^{\circ} - 43^{\circ}) \dots \tan (90^{\circ} - 1^{\circ}) \\ = \tan 1^{\circ} \cdot \cot 1^{\circ} \cdot \tan 2^{\circ} \cdot \cot 2^{\circ} \dots \tan 89^{\circ} \cdot \cot 89^{\circ} \\ = 1 \cdot 1 \dots 1 \cdot 1 = 1 \end{aligned}$

Option (a) 0: The product of the tangent values from (1^\circ) to (89^\circ) cannot be zero because none of the individual tangent values are zero within this range. The tangent function is zero only at integer multiples of (180^\circ), which are not included in the given range.
Option (c) (\frac{1}{2}): The product of the tangent values from (1^\circ) to (89^\circ) does not simplify to (\frac{1}{2}). The correct simplification, as shown in the solution, results in 1 due to the pairing of (\tan x) and (\cot x) which each multiply to 1.
Option (d) Not defined: The product of the tangent values from (1^\circ) to (89^\circ) is defined. Each tangent value within this range is finite and non-zero, and their product is well-defined and equals 1.

35. The value of $\frac{1 - \tan^{2} 15^{\circ}}{1 + \tan^{2} 15^{\circ}}$ is

(a) 1

(b) $\sqrt{3}$

(d) 2

Show Answer

Solution

$\begin{aligned} Let θ = 15^{\circ} \\ We know that, \cos 2 θ = \overset{―}{1 + \tan^{2} θ} \\ ∴ \cos 30^{\circ} = \frac{1 - \tan^{2} 15^{\circ}}{1 + \tan^{2} 15^{\circ}} \\ \Rightarrow \frac{1 - \tan^{2} 15^{\circ}}{1 + \tan^{2} 15^{\circ}} = \frac{\sqrt{3}}{2} [∵ \cos 30^{\circ} = \frac{\sqrt{3}}{2}] \end{aligned}$

Option (a) 1: This option is incorrect because the value of (\frac{1-\tan^2 15^\circ}{1+\tan^2 15^\circ}) is not equal to 1. The expression simplifies to (\cos 30^\circ), which is (\frac{\sqrt{3}}{2}), not 1.
Option (b) (\sqrt{3}): This option is incorrect because (\cos 30^\circ) is (\frac{\sqrt{3}}{2}), not (\sqrt{3}). The given expression (\frac{1-\tan^2 15^\circ}{1+\tan^2 15^\circ}) simplifies to (\cos 30^\circ), which is (\frac{\sqrt{3}}{2}).
Option (d) 2: This option is incorrect because the value of (\cos 30^\circ) is (\frac{\sqrt{3}}{2}), not 2. The expression (\frac{1-\tan^2 15^\circ}{1+\tan^2 15^\circ}) simplifies to (\cos 30^\circ), which is (\frac{\sqrt{3}}{2}).

36. The value of $\cos 1^{\circ} \cos 2^{\circ} \cos 3^{\circ} \dots \cos 179^{\circ}$ is

(a) $\frac{1}{\sqrt{2}}$

(b) 0

(d) -1

Show Answer

Solution

(b) Given expression, $\cos 1^{\circ} \cos 2^{\circ} \cos 3^{\circ} \dots \cos 179^{\circ}$

$\begin{aligned} = \cos 1^{\circ} \cos 2^{\circ} \dots \cos 90^{\circ} \dots \cos 179^{\circ} [∵ \cos 90^{\circ} = 0] \\ = 0 \end{aligned}$

Option (a) $\frac{1}{\sqrt{2}}$ is incorrect because the product of cosines from $1^{\circ}$ to $179^{\circ}$ includes $\cos 90^{\circ}$ , which is 0. Therefore, the entire product is 0, not $\frac{1}{\sqrt{2}}$ .
Option (c) 1 is incorrect because, as mentioned, the product includes $\cos 90^{\circ}$ , which is 0. Hence, the product cannot be 1.
Option (d) -1 is incorrect because the product includes $\cos 90^{\circ}$ , which is 0. Therefore, the product cannot be -1.

37. If $\tan θ = 3$ and $θ$ lies in third quadrant, then the value of $\sin θ$ is

(a) $\frac{1}{\sqrt{10}}$

(b) $- \frac{1}{\sqrt{10}}$

(d) $\frac{3}{\sqrt{10}}$

Show Answer

Solution

(c)

$Given that, \tan θ = 3$

$\Rightarrow \sec^{2} θ = 1 + \tan^{2} θ$

$\Rightarrow \sec θ = \sqrt{1 + 9} = \pm \sqrt{10}$

$\Rightarrow \sec θ = - \sqrt{10}$

$\Rightarrow \cos θ = - \frac{1}{\sqrt{10}}$

$\Rightarrow \sin θ = \pm \sqrt{1 - \frac{1}{10}} = \pm \sqrt{\frac{9}{10}} = \pm \frac{3}{\sqrt{10}}$ [since, $θ$ lies in third quadrant]

$∴ \sin θ = - \frac{3}{\sqrt{10}}$

Option (a) $\frac{1}{\sqrt{10}}$ : This option is incorrect because in the third quadrant, both sine and cosine functions are negative. Since $\sin θ$ must be negative in the third quadrant, $\frac{1}{\sqrt{10}}$ is not a valid value for $\sin θ$ .
Option (b) $- \frac{1}{\sqrt{10}}$ : This option is incorrect because it does not satisfy the relationship between $\sin θ$ and $\tan θ$ . Given $\tan θ = 3$ , we have $\sin θ = - \frac{3}{\sqrt{10}}$ and not $- \frac{1}{\sqrt{10}}$ .
Option (d) $\frac{3}{\sqrt{10}}$ : This option is incorrect because in the third quadrant, the sine function is negative. Therefore, $\sin θ$ cannot be positive, and $\frac{3}{\sqrt{10}}$ is not a valid value for $\sin θ$ .

38. The value of $\tan 75^{\circ} - \cot 75^{\circ}$ is

(a) $2 \sqrt{3}$

(b) $2 + \sqrt{3}$

(d) 1

Show Answer

Solution

(a) Given expression, $\tan 75^{\circ} - \cot 75^{\circ}$

$\begin{aligned} = \frac{\sin 75^{\circ}}{\cos 75^{\circ}} - \frac{\cos 75^{\circ}}{\sin 75^{\circ}} \\ = \frac{\sin^{2} 75^{\circ} - \cos^{2} 75^{\circ}}{\sin 75^{\circ} \cdot \cos_{7}^{\circ}} \\ = \frac{- 2 \cos 150^{\circ}}{\sin 150^{\circ}} \\ = \frac{- 2 \cos (90^{\circ} + 60^{\circ})}{\sin (90^{\circ} + 60^{\circ})} \\ = \frac{+ 2 \sin 60^{\circ}}{\cos 60^{\circ}} \\ = \frac{2 \cdot \frac{\sqrt{3}}{2}}{\frac{1}{2}} = 2 \sqrt{3} \end{aligned}$

Option (b) $2 + \sqrt{3}$ : This option is incorrect because the correct simplification of $\tan 75^{\circ} - \cot 75^{\circ}$ results in $2 \sqrt{3}$ , not a sum involving $\sqrt{3}$ . The trigonometric identities and simplifications do not lead to an expression of the form $2 + \sqrt{3}$ .
Option (c) $2 - \sqrt{3}$ : This option is incorrect because the correct simplification of $\tan 75^{\circ} - \cot 75^{\circ}$ results in $2 \sqrt{3}$ , not a difference involving $\sqrt{3}$ . The trigonometric identities and simplifications do not lead to an expression of the form $2 - \sqrt{3}$ .
Option (d) 1: This option is incorrect because the correct simplification of $\tan 75^{\circ} - \cot 75^{\circ}$ results in $2 \sqrt{3}$ , not a simple integer like 1. The trigonometric identities and simplifications do not lead to a value of 1.

39. Which of the following is correct?

(a) $\sin 1^{\circ} > \sin 1$

(b) $\sin 1^{\circ} < \sin 1$

(d) $\sin 1^{\circ} = \frac{π}{18^{\circ}} \sin 1$

Show Answer

Solution

(b) We know that, if $θ$ is increasing, then $\sin θ$ is also increasing.

$∴ \sin 1^{\circ} < \sin 1 [∵ 1 r a d = 57^{\circ 30}]$

Option (a): $\sin 1^{\circ} > \sin 1$ is incorrect because, in the range of angles from $0$ to $90$ degrees, the sine function is increasing. Since $1$ degree is much smaller than $1$ radian (approximately $57.3$ degrees), $\sin 1^{\circ}$ will be less than $\sin 1$ .
Option (c): $\sin 1^{\circ} = \sin 1$ is incorrect because $1$ degree and $1$ radian are not the same measure. $1$ radian is approximately $57.3$ degrees, so $\sin 1^{\circ}$ and $\sin 1$ cannot be equal.
Option (d): $\sin 1^{\circ} = \frac{π}{18^{\circ}} \sin 1$ is incorrect because the expression $\frac{π}{18^{\circ}}$ does not make sense dimensionally. The sine function takes an angle as input, and $\frac{π}{18^{\circ}}$ is not a valid angle measure. Additionally, there is no known trigonometric identity that relates $\sin 1^{\circ}$ to $\sin 1$ in this manner.

40. If $\tan α = \frac{m}{m + 1}$ and $\tan β = \frac{1}{2 m + 1}$ , then $α + β$ is equal to

(a) $\frac{π}{2}$

(b) $\frac{π}{3}$

(d) $\frac{π}{4}$

Show Answer

Solution

(d) Given that, $\tan α = \frac{m}{m + 1}$ and $\tan β = \frac{1}{2 m + 1}$

Now, $\tan (α + β) = \frac{\tan α + \tan β}{1 - \tan α \cdot \tan β}$

$\begin{matrix} \Rightarrow & \tan (α + β) = \frac{\frac{m}{m + 1} + \frac{1}{2 m + 1}}{1 - \frac{m}{m + 1} \frac{1}{2 m + 1}} \\ \Rightarrow & \tan (α + β) = \frac{m (2 m + 1) + m + 1}{(m + 1) (2 m + 1) - m} \\ \Rightarrow & \tan (α + β) = \frac{2 m^{2} + m + m + 1}{2 m^{2} + 2 m + m + 1 - m} \\ \Rightarrow & \tan (α + β) = \frac{2 m^{2} + 2 m + 1}{2 m^{2} + 2 m + 1} \Rightarrow \tan (α + β) = 1 \\ ∴ & α + β = \frac{π}{4} \end{matrix}$

Option (a) $\frac{π}{2}$ : This option is incorrect because if $α + β = \frac{π}{2}$ , then $\tan (α + β)$ would be undefined (since $\tan (\frac{π}{2})$ is undefined). However, in the given solution, $\tan (α + β) = 1$ , which is a defined value.
Option (b) $\frac{π}{3}$ : This option is incorrect because if $α + β = \frac{π}{3}$ , then $\tan (α + β) = \sqrt{3}$ . However, in the given solution, $\tan (α + β) = 1$ , which does not equal $\sqrt{3}$ .
Option (c) $\frac{π}{6}$ : This option is incorrect because if $α + β = \frac{π}{6}$ , then $\tan (α + β) = \frac{1}{\sqrt{3}}$ . However, in the given solution, $\tan (α + β) = 1$ , which does not equal $\frac{1}{\sqrt{3}}$ .

41. The minimum value of $3 \cos x + 4 \sin x + 8$ is

(a) 5

(b) 9

(d) 3

Show Answer

Thinking Process

For the expression $A \cos θ + B \sin θ$ , then the minimum value is $- \sqrt{A^{2} + B^{2}}$ .

Solution

(d) Given expression, $3 \cos x + 4 \sin x + 8$

$\begin{matrix} Let & y = 3 \cos x + 4 \sin x + 8 \\ \Rightarrow & y - 8 = 3 \cos x + 4 \sin x \\ ∴ & Minimum value of y - 8 = - \sqrt{9 + 16} \\ \Rightarrow & y - 8 = - 5 \Rightarrow y = - 5 + 8 \\ ∴ & y = 3 \end{matrix}$

Hence, the minimum value of $3 \cos x + 4 \sin x + 8$ is 3 .

Option (a) 5: This is incorrect because the minimum value of the expression $3 \cos x + 4 \sin x + 8$ is calculated to be 3, not 5. The calculation shows that the minimum value of $3 \cos x + 4 \sin x$ is $- 5$ , and adding 8 to this gives 3.
Option (b) 9: This is incorrect because the minimum value of the expression $3 \cos x + 4 \sin x + 8$ is 3, not 9. The calculation shows that the minimum value of $3 \cos x + 4 \sin x$ is $- 5$ , and adding 8 to this gives 3.
Option (c) 7: This is incorrect because the minimum value of the expression $3 \cos x + 4 \sin x + 8$ is 3, not 7. The calculation shows that the minimum value of $3 \cos x + 4 \sin x$ is $- 5$ , and adding 8 to this gives 3.

42. The value of $\tan 3 A - \tan 2 A - \tan A$ is

(a) $\tan 3 A \tan 2 A \tan A$

(b) $- \tan 3 A \tan 2 A \tan A$

(d) None of the above

Show Answer

Solution

(a)

$\begin{aligned} Let 3 A & = A + 2 A \\ \tan 3 A & = \tan (A + 2 A) \end{aligned}$

$\Rightarrow \tan 3 A = \frac{\tan A + \tan 2 A}{1 - \tan A \cdot \tan 2 A}$

$\Rightarrow \tan A + \tan 2 A = \tan 3 A - \tan 3 A \cdot \tan 2 A \cdot \tan A$

$\Rightarrow \tan 3 A - \tan 2 A - \tan A = \tan 3 A \cdot \tan 2 A \cdot \tan A$

Option (b): The expression $- \tan 3 A \tan 2 A \tan A$ is incorrect because the correct expression derived from the given trigonometric identity is $\tan 3 A \cdot \tan 2 A \cdot \tan A$ without the negative sign. The negative sign would change the value and does not match the derived result.
Option (c): The expression $\tan A \tan 2 A - \tan 2 A \tan 3 A - \tan 3 A \tan A$ is incorrect because it does not simplify to the given expression $\tan 3 A - \tan 2 A - \tan A$ . The correct derivation involves the product of the three tangent terms, not a combination of products and differences.
Option (d): This option is incorrect because option (a) is the correct answer, as shown by the derivation. Therefore, “None of the above” is not applicable.

43. The value of $\sin (45^{\circ} + θ) - \cos (45^{\circ} - θ)$ is

(a) $2 \cos θ$

(b) $2 \sin θ$

(d) 0

Show Answer

Thinking Process

Use formula i.e., $\sin (A + B) = \sin A \cos B + \cos A \sin B$ and $\cos (A - B) = \cos A \cos B + \sin A \sin B$ .

Solution

(d) Given expression,

$\begin{aligned} \sin (45^{\circ} + θ) & - \cos (45^{\circ} - θ) \\ = \sin 45^{\circ} \cdot \cos θ + \cos 45^{\circ} \cdot \sin θ - \cos 45^{\circ} \cdot \cos θ - \sin 45^{\circ} \cdot \sin θ \\ = \frac{1}{\sqrt{2}} \cdot \cos θ + \frac{1}{\sqrt{2}} \cdot \sin θ - \frac{1}{\sqrt{2}} \cdot \cos θ - \frac{1}{\sqrt{2}} \sin θ \\ = 0 \end{aligned}$

Option (a) $2 \cos θ$ : This option is incorrect because the given expression simplifies to zero, not to $2 \cos θ$ . The terms involving $\cos θ$ and $\sin θ$ cancel each other out, resulting in zero.
Option (b) $2 \sin θ$ : This option is incorrect because the given expression simplifies to zero, not to $2 \sin θ$ . The terms involving $\cos θ$ and $\sin θ$ cancel each other out, resulting in zero.
Option (c) 1: This option is incorrect because the given expression simplifies to zero, not to 1. The terms involving $\cos θ$ and $\sin θ$ cancel each other out, resulting in zero.

44. The value of $\cot (\frac{π}{4} + θ) \cot (\frac{π}{4} - θ)$ is

(a) -1

(b) 0

(d) Not defined

Show Answer

Thinking Process

$Use formula i.e., (\cot (A + B) = \frac{\cot A \cot B - 1}{\cot A + \cot B}) and \cot (A - B) = (\frac{\cot A \cot B + 1}{\cot A - \cot B})$

Solution

(c)

$\begin{aligned} Given expression, (\cot \frac{π}{4} + θ) - \cot (\frac{π}{4} - θ) \\ = (\frac{\cot \frac{π}{4} \cot θ - 1}{\cot \frac{π}{4} + \cot θ}) \cdot (\frac{\cot \frac{π}{4} \cot θ + 1}{\cot θ - \cot \frac{π}{4}}) \\ = (\frac{\cot θ - 1}{\cot θ + 1}) \cdot (\frac{\cot θ + 1}{\cot θ - 1}) \\ = 1 \end{aligned}$

Option (a) -1: This option is incorrect because the product of the cotangent functions in the given expression simplifies to 1, not -1. The cotangent function does not introduce a negative sign in this context.
Option (b) 0: This option is incorrect because the product of the cotangent functions in the given expression does not result in zero. The cotangent values and their product do not lead to a zero value in this scenario.
Option (d) Not defined: This option is incorrect because the expression is defined for all values of (\theta) where the cotangent functions are defined. There are no values of (\theta) that make the expression undefined within the given context.

45. $\cos 2 θ \cos 2 φ + \sin^{2} (θ - φ) - \sin^{2} (θ + φ)$ is equal to

(a) $\sin 2 (θ + φ)$

(b) $\cos 2 (θ + φ)$

(d) $\cos 2 (θ - φ)$

Show Answer

Solution

(b) Given expression, $\cos 2 θ \cos 2 φ + \sin^{2} (θ - φ) - \sin^{2} (θ + φ)$

$\begin{aligned} = \cos 2 θ \cdot \cos 2 φ + \sin (θ - φ + θ + φ) \cdot \sin (θ - φ - θ - φ) \\ = \cos 2 θ \cdot \cos 2 φ - \sin 2 θ \cdot \sin 2 φ \\ = \cos (2 θ + 2 φ) = \cos 2 (θ + φ) \end{aligned}$

Option (a) $\sin 2 (θ + φ)$ : This option is incorrect because the given expression simplifies to a cosine function, not a sine function. The trigonometric identities used in the simplification process lead to a cosine term, specifically $\cos 2 (θ + φ)$ , rather than a sine term.
Option (c) $\sin 2 (θ - φ)$ : This option is incorrect because the given expression does not involve the sine of the difference of the angles $θ$ and $φ$ . The simplification process shows that the expression involves the sum of the angles, not their difference.
Option (d) $\cos 2 (θ - φ)$ : This option is incorrect because the given expression simplifies to $\cos 2 (θ + φ)$ , not $\cos 2 (θ - φ)$ . The trigonometric identities used in the solution clearly indicate that the sum of the angles is involved, not the difference.

46. The value of $\cos 12^{\circ} + \cos 84^{\circ} + \cos 156^{\circ} + \cos 132^{\circ}$ is

(a) $\frac{1}{2}$

(b) 1

(d) $\frac{1}{8}$

Show Answer

Thinking Process

Use the formula $\cos A + \cos B = 2 \cos \frac{A + B}{2} \cdot \cos \frac{A - B}{2}$ and

$\cos A - \cos B = - 2 \sin \frac{A + B}{2} \cdot \sin \frac{A - B}{2}$ to solve this problem.

Solution

$= \cos 12^{\circ} + \cos 150^{\circ} + \cos 84^{\circ} + \cos 132^{\circ}$

$= 2 \cos (\frac{12^{\circ} + 150^{\circ}}{2}) \cdot \cos (\frac{12^{\circ} - 150^{\circ}}{2}) + 2 \cos (\frac{84^{\circ} + 132^{\circ}}{2}) \cdot \cos (\frac{84^{\circ} - 132^{\circ}}{2})$

$= 2 \cos 84^{\circ} \cos 72^{\circ} + 2 \cos 108^{\circ} \cdot \cos 24^{\circ}$

$= 2 \cos 84^{\circ} \cos (90^{\circ} - 18^{\circ}) + 2 \cos (90^{\circ} + 18^{\circ}) \cdot \cos 24^{\circ}$

$= 2 \cos 84^{\circ} \sin 18^{\circ} - 2 \sin 18^{\circ} \cdot \cos 24^{\circ}$

$= 2 \sin 18^{\circ} (\cos 84^{\circ} - \cos 24^{\circ})$

$= 2 \sin 18^{\circ} \cdot 2 \sin (\frac{84^{\circ} + 24^{\circ}}{2}) \cdot \sin (\frac{84^{\circ} - 24^{\circ}}{2})$

$= - 4 \sin 18^{\circ} \cdot \sin 54^{\circ} \sin 30^{\circ}$

$= - 4 \frac{\sqrt{5} - 1}{4} \cdot \cos 36^{\circ} \cdot \frac{1}{2}$

$= - (\sqrt{5} - 1) \frac{\sqrt{5} + 1}{4} \cdot \frac{1}{2} = - \frac{5 - 1}{8} = \frac{- 4}{8} = \frac{- 1}{2}$

Option (a) $\frac{1}{2}$ : This option is incorrect because the sum of the given cosine values does not simplify to a positive fraction. The detailed trigonometric manipulations and identities used in the solution show that the result is negative, specifically $- \frac{1}{2}$ .
Option (b) 1: This option is incorrect because the sum of the given cosine values does not equal 1. The trigonometric identities and calculations used in the solution demonstrate that the sum is negative, not positive, and certainly not equal to 1.
Option (d) $\frac{1}{8}$ : This option is incorrect because the sum of the given cosine values does not simplify to a small positive fraction like $\frac{1}{8}$ . The detailed solution shows that the sum is $- \frac{1}{2}$ , which is a negative value and not a small positive fraction.

47. If $\tan A = \frac{1}{2}$ and $\tan B = \frac{1}{3}$ , then $\tan (2 A + B)$ is equal to

(a) 1

(b) 2

(d) 4

Show Answer

Solution

Now, $\tan (2 A + B) = \frac{\tan 2 A + \tan B}{1 - \tan 2 A \cdot \tan B}$

Also, $\tan 2 A = \frac{2 \tan A}{1 - \tan^{2} A} = \frac{2 \cdot \frac{1}{2}}{1 - \frac{1}{4}} = \frac{4}{3}$

From Eq. (i), $\tan (2 A + B) = \frac{\frac{4}{3} + \frac{1}{3}}{1 - \frac{4}{3} \cdot \frac{1}{3}} = \frac{\frac{4}{3} + \frac{1}{3}}{\frac{9 - 4}{9}} = \frac{\frac{5}{3}}{\frac{5}{9}} = 3$

Option (a) 1: This option is incorrect because the calculated value of (\tan(2A + B)) is 3, not 1. The mathematical operations and trigonometric identities used in the solution do not yield 1.
Option (b) 2: This option is incorrect because the calculated value of (\tan(2A + B)) is 3, not 2. The intermediate steps involving (\tan 2A) and the final formula for (\tan(2A + B)) do not result in 2.
Option (d) 4: This option is incorrect because the calculated value of (\tan(2A + B)) is 3, not 4. The correct application of trigonometric identities and simplification steps do not lead to 4.

48. The value of $\sin \frac{π}{10} \sin \frac{13 π}{10}$ is

(a) $\frac{1}{2}$

(b) $- \frac{1}{2}$

(d) 1

Show Answer

Solution

$\begin{aligned} = - \sin \frac{π}{10} \sin \frac{3 π}{10} = - \sin 18^{\circ} \cdot \sin 54^{\circ} \\ = - \sin 18^{\circ} \cdot \cos 36^{\circ} \\ = - \frac{\sqrt{5} - 1}{4} \frac{\sqrt{5} + 1}{4} [since,put this value here] \\ = - \frac{5 - 1}{16} = - \frac{1}{4} \end{aligned}$

Option (a) $\frac{1}{2}$ : This option is incorrect because the product of $\sin \frac{π}{10}$ and $\sin \frac{13 π}{10}$ does not simplify to $\frac{1}{2}$ . The trigonometric identities and values involved do not yield this result.
Option (b) $- \frac{1}{2}$ : This option is incorrect because the product of $\sin \frac{π}{10}$ and $\sin \frac{13 π}{10}$ does not simplify to $- \frac{1}{2}$ . The correct simplification using trigonometric identities results in a different value.
Option (d) 1: This option is incorrect because the product of $\sin \frac{π}{10}$ and $\sin \frac{13 π}{10}$ does not simplify to 1. The trigonometric identities and values involved do not yield this result.

49. The value of $\sin 50^{\circ} - \sin 70^{\circ} + \sin 10^{\circ}$ is

(a) 1

(b) 0

(d) 2

Show Answer

Thinking Process

Here, use the formula i.e., $\sin A - \sin B = 2 \cos \frac{A + B}{2} \cdot \sin \frac{A - B}{2}$ also $\sin (- θ) = - \sin θ$

Solution

(b) Given expression, $\sin 50^{\circ} - \sin 70^{\circ} + \sin 10^{\circ}$

$\begin{aligned} = 2 \cos (\frac{50^{\circ} + 70^{\circ}}{2}) \cdot \sin (\frac{50^{\circ} - 70^{\circ}}{2} + \sin 10^{\circ}) \\ = - 2 \cos 60^{\circ} \sin 10^{\circ} + \sin 10^{\circ} \\ = - 2 \cdot \frac{1}{2} \sin 10^{\circ} + \sin 10^{\circ} = 0 \end{aligned}$

Option (a) 1: The given expression $\sin 50^{\circ} - \sin 70^{\circ} + \sin 10^{\circ}$ simplifies to 0, not 1. The trigonometric identities and simplifications used in the solution show that the terms cancel each other out, resulting in 0.
Option (c) $\frac{1}{2}$ : The simplification of the given expression does not yield $\frac{1}{2}$ . The correct simplification using trigonometric identities results in 0, not $\frac{1}{2}$ .
Option (d) 2: The given expression $\sin 50^{\circ} - \sin 70^{\circ} + \sin 10^{\circ}$ does not simplify to 2. The trigonometric identities and calculations show that the terms cancel each other out, resulting in 0, not 2.

50. If $\sin θ + \cos θ = 1$ , then the value of $\sin 2 θ$ is

(a) 1

(b) $\frac{1}{2}$

(d) -1

Show Answer

Solution

On squaring both sides, we get

$\sin^{2} θ + \cos^{2} θ + 2 \sin θ \cdot \cos θ = 1$

$\Rightarrow 1 + \sin 2 θ = 1$

$∴ \sin 2 θ = 0$

Option (a) 1: If (\sin 2\theta = 1), then (\sin \theta) and (\cos \theta) would need to satisfy (\sin 2\theta = 2\sin \theta \cos \theta = 1). However, given (\sin \theta + \cos \theta = 1), this condition cannot be met because the maximum value of (\sin \theta) and (\cos \theta) is (\frac{\sqrt{2}}{2}), which does not satisfy the equation.
Option (b) (\frac{1}{2}): If (\sin 2\theta = \frac{1}{2}), then (2\sin \theta \cos \theta = \frac{1}{2}). This would imply (\sin \theta \cos \theta = \frac{1}{4}). However, given (\sin \theta + \cos \theta = 1), this condition cannot be met because the values of (\sin \theta) and (\cos \theta) that satisfy this equation do not result in (\sin \theta \cos \theta = \frac{1}{4}).
Option (d) -1: If (\sin 2\theta = -1), then (2\sin \theta \cos \theta = -1). This would imply (\sin \theta \cos \theta = -\frac{1}{2}). However, given (\sin \theta + \cos \theta = 1), this condition cannot be met because the values of (\sin \theta) and (\cos \theta) that satisfy this equation do not result in (\sin \theta \cos \theta = -\frac{1}{2}).

51. If $α + β = \frac{π}{4}$ , then the value of $(1 + \tan α) (1 + \tan β)$ is

(a) 1

(b) 2

(d) Not defined

Show Answer

Thinking Process

Formula i.e., $\tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \cdot \tan B}$ to solve this problem.

Solution

(b) Given that, $α + β = \frac{π}{4}$

Now, $(1 + \tan α) (1 + \tan β) = 1 + \tan α + \tan β + \tan α \tan β \dots (i)$

We know that, $\tan (α + β) = \frac{\tan α + \tan β}{1 - \tan α \cdot \tan β}$

$\begin{aligned} \Rightarrow 1 = \frac{\tan α + \tan β}{1 - \tan α \cdot \tan β} . . (i) \\ \Rightarrow \tan α + \tan β = 1 - \tan α \tan β \end{aligned}$

From Eq. (i),

$\begin{aligned} (1 + \tan α) (1 + \tan β) & = 1 + 1 - \tan α \cdot \tan β + \tan α \cdot \tan β \\ = 2 \end{aligned}$

Option (a) 1: This option is incorrect because the expression ((1 + \tan \alpha)(1 + \tan \beta)) simplifies to 2, not 1. The calculation shows that the sum of the terms results in 2.
Option (c) -2: This option is incorrect because the expression ((1 + \tan \alpha)(1 + \tan \beta)) does not yield a negative value. The terms involved are positive and their sum results in 2.
Option (d) Not defined: This option is incorrect because the expression ((1 + \tan \alpha)(1 + \tan \beta)) is well-defined for the given condition (\alpha + \beta = \frac{\pi}{4}). The trigonometric identities used in the solution are valid and lead to a defined numerical result.

52. If $\sin θ = \frac{- 4}{5}$ and $θ$ lies in third quadrant, then the value of $\cos \frac{θ}{2}$ is

(a) $\frac{1}{5}$

(b) $- \frac{1}{\sqrt{10}}$

(d) $\frac{1}{\sqrt{10}}$

Show Answer

Thinking Process

Use $\cos θ = \sqrt{1 - \sin^{2} θ}$ and $\cos θ = 2 \cos^{2} \frac{θ}{2} - 1$ .

Solution

$\begin{aligned} \cos θ & = \sqrt{1 - \frac{16}{25}} = \sqrt{\frac{25 - 16}{25}} = \pm \frac{3}{5} \\ \cos θ & = \frac{- 3}{5} [since, θ lies in third quadrant] \\ \Rightarrow 2 \cos^{2} \frac{θ}{2} - 1 & = \frac{- 3}{5} \\ \Rightarrow 2 \cos^{2} \frac{θ}{2} & = 1 - \frac{3}{5} \\ \Rightarrow 2 \cos^{2} \frac{θ}{2} & = \frac{2}{5} \\ ∴ \cos^{\frac{θ}{2}} & = \pm \frac{1}{\sqrt{5}} \\ \Rightarrow \cos \frac{θ}{2} & = - \frac{1}{\sqrt{5}} [since, θ lies in third quadrant] \end{aligned}$

Option (a) $\frac{1}{5}$ : This value is incorrect because it does not satisfy the equation derived from the given trigonometric identity. Specifically, $\cos \frac{θ}{2}$ must satisfy the equation $2 \cos^{2} \frac{θ}{2} = \frac{2}{5}$ , which simplifies to $\cos^{2} \frac{θ}{2} = \frac{1}{5}$ . Therefore, $\cos \frac{θ}{2}$ must be $\pm \frac{1}{\sqrt{5}}$ , not $\frac{1}{5}$ .
Option (b) $- \frac{1}{\sqrt{10}}$ : This value is incorrect because it does not satisfy the equation $2 \cos^{2} \frac{θ}{2} = \frac{2}{5}$ . If $\cos \frac{θ}{2} = - \frac{1}{\sqrt{10}}$ , then $\cos^{2} \frac{θ}{2} = \frac{1}{10}$ , which does not match $\frac{1}{5}$ .
Option (d) $\frac{1}{\sqrt{10}}$ : This value is incorrect for the same reason as option (b). If $\cos \frac{θ}{2} = \frac{1}{\sqrt{10}}$ , then $\cos^{2} \frac{θ}{2} = \frac{1}{10}$ , which does not match $\frac{1}{5}$ . Additionally, since $θ$ lies in the third quadrant, $\cos \frac{θ}{2}$ should be negative, not positive.

53. The number of solutions of equation $\tan x + \sec x = 2 \cos x$ lying in the interval $[0, 2 π]$ is

(a) 0

(b) 1

(d) 3

Show Answer

Solution

$\Rightarrow \tan + \sec x = 2 \cos x$

$\Rightarrow \frac{\sin x}{\cos x} + \frac{1}{\cos x} = 2 \cos x$

$\Rightarrow 1 + \sin x = 2 \cos^{2} x$

$1 + \sin x = 2 (1 - \sin^{2} x)$

$\Rightarrow 1 + \sin x = 2 - 2 \sin^{2} x$

$\Rightarrow 2 \sin^{2} x + \sin x - 1 = 0$

$\Rightarrow 2 \sin^{2} x + 2 \sin x - \sin x - 1 = 0$

$\Rightarrow 2 \sin x (\sin x + 1) - 1 (\sin x + 1) = 0$

$\Rightarrow (\sin x + 1) (2 \sin x - 1) = 0$

$\Rightarrow \sin x + 1 = 0$ or $(2 \sin x - 1) = 0$

$\Rightarrow \sin x = - 1, \sin x = \frac{1}{2}$

$∴ x = \frac{3 π}{2}, x = \frac{π}{6}$

Hence, only two solutions possible.

Option (a) is incorrect because there are indeed solutions to the equation $\tan x + \sec x = 2 \cos x$ within the interval $[0, 2 π]$ . Specifically, the solutions are $x = \frac{3 π}{2}$ and $x = \frac{π}{6}$ .
Option (b) is incorrect because there is more than one solution to the equation within the interval $[0, 2 π]$ . The correct number of solutions is two.
Option (d) is incorrect because there are not three solutions to the equation within the interval $[0, 2 π]$ . The correct number of solutions is two.

54. The value of $\sin \frac{π}{18} + \sin \frac{π}{9} + \sin \frac{2 π}{9} + \sin \frac{5 π}{18}$ is

(a) $\sin \frac{7 π}{18} + \sin \frac{4 π}{9}$

(b) 1

(d) $\cos \frac{π}{9} + \sin \frac{π}{9}$

Show Answer

Thinking Process

Here, apply the formulae i.e., $\sin A + \sin B = 2 \sin \frac{A + B}{2} \cos \frac{A - B}{2}$ .

Solution

(a) Given expression, $\sin \frac{π}{18} + \sin \frac{π}{9} + \sin \frac{2 π}{9} + \sin \frac{5 π}{18}$

$\begin{aligned} = \sin 10^{\circ} + \sin 20^{\circ} + \sin 40^{\circ} + \sin 50^{\circ} \\ = \sin 50^{\circ} + \sin 10^{\circ} + \sin 40^{\circ} + \sin 20^{\circ} \\ = \sin 130^{\circ} + \sin 10^{\circ} + \sin 140^{\circ} + \sin 20^{\circ} \\ = 2 \sin 70^{\circ} \cos 60^{\circ} + 2 \sin 80^{\circ} \cdot \cos 60^{\circ} [∵ \sin x + \sin y = 2 \sin \frac{x + y}{2} \cdot \cos \frac{x - y}{2}] \\ = 2 \cdot \frac{1}{2} \sin 70^{\circ} + 2 \cdot \frac{1}{2} \sin 80^{\circ} [∵ \cos 60^{\circ} = \frac{1}{2}] \\ = \sin 70^{\circ} + \sin 80^{\circ} = \sin \frac{7 π}{18} + \sin \frac{4 π}{9} \end{aligned}$

Option (b) 1: The given expression $\sin \frac{π}{18} + \sin \frac{π}{9} + \sin \frac{2 π}{9} + \sin \frac{5 π}{18}$ does not simplify to 1. The trigonometric identities and angle sum formulas used in the solution show that the expression simplifies to $\sin \frac{7 π}{18} + \sin \frac{4 π}{9}$ , not 1.
Option (c) $\cos \frac{π}{6} + \cos \frac{3 π}{7}$ : The given expression involves only sine functions, and there is no transformation or identity that converts it into a sum of cosine functions like $\cos \frac{π}{6} + \cos \frac{3 π}{7}$ . The angles involved in the original expression do not correspond to the angles in the cosine terms provided in this option.
Option (d) $\cos \frac{π}{9} + \sin \frac{π}{9}$ : The given expression $\sin \frac{π}{18} + \sin \frac{π}{9} + \sin \frac{2 π}{9} + \sin \frac{5 π}{18}$ does not simplify to a combination of $\cos \frac{π}{9}$ and $\sin \frac{π}{9}$ . The trigonometric identities used in the solution show that the expression simplifies to $\sin \frac{7 π}{18} + \sin \frac{4 π}{9}$ , which does not match the form of $\cos \frac{π}{9} + \sin \frac{π}{9}$ .

55. If $A$ lies in the second quadrant and $3 \tan A + 4 = 0$ , then the value of $2 \cot A - 5 \cos A + \sin A$ is

(a) $\frac{- 53}{10}$

(b) $\frac{23}{10}$

(d) $\frac{7}{10}$

Show Answer

Thinking Process

Use the formulae i.e., $\sec A = \sqrt{1 + \tan^{2} A}$ and $\sin A = \sqrt{1 - \cos^{2} A}, \sec A = \frac{1}{\cos A}$ and $\tan A = \frac{1}{\cot A}$ .

Solution (b)

$\begin{aligned} Given equation, 3 \tan A + 4 = 0 \\ \Rightarrow 3 \tan A = - 4 \\ \Rightarrow \tan A = \frac{- 4}{3} \\ \Rightarrow \cot A = \frac{- 3}{4} \\ \Rightarrow \sec A = \sqrt{1 + \frac{16}{9}} = \sqrt{\frac{25}{9}} = \pm \frac{5}{3} [since, A lies in second quadrant] \\ \Rightarrow \sec A = \frac{- 5}{3} \\ \cos A = \frac{- 3}{5} \\ \sin A = \sqrt{1 - \frac{9}{25}} = \frac{\sqrt{25 - 9}}{25} = \pm \frac{4}{5} \\ \sin A = \frac{4}{5} \end{aligned} [since, A lies in second quadrant]$

$\begin{aligned} ∴ 2 \cot A - 5 \cos A + \sin A & = 2 \frac{- 3}{4} - 5 \frac{- 3}{5} + \frac{4}{5} \\ = \frac{- 6}{4} + 3 + \frac{4}{5} \\ = \frac{- 30 + 60 + 16}{20} = \frac{46}{20} \\ = \frac{23}{10} \end{aligned}$

Option (a) $\frac{- 53}{10}$ : This option is incorrect because the calculations for $2 \cot A - 5 \cos A + \sin A$ do not yield a negative value. The correct value is positive, as shown in the solution.
Option (c) $\frac{37}{10}$ : This option is incorrect because the calculations for $2 \cot A - 5 \cos A + \sin A$ result in $\frac{23}{10}$ , not $\frac{37}{10}$ . The arithmetic steps in the solution confirm this.
Option (d) $\frac{7}{10}$ : This option is incorrect because the calculations for $2 \cot A - 5 \cos A + \sin A$ result in $\frac{23}{10}$ , not $\frac{7}{10}$ . The detailed steps in the solution show that the correct value is $\frac{23}{10}$ .

56. The value of $\cos^{2} 48^{\circ} - \sin^{2} 12^{\circ}$ is

(a) $\frac{\sqrt{5} + 1}{8}$

(b) $\frac{\sqrt{5} - 1}{8}$

(d) $\frac{\sqrt{5} + 1}{2 \sqrt{2}}$

Show Answer

Solution

(a) Given expression, $\cos^{2} 48^{\circ} - \sin^{2} 12^{\circ}$

$\begin{aligned} = \cos (48^{\circ} + 12^{\circ}) - \cos (48^{\circ} - 12^{\circ}) \\ = \cos 60^{\circ} \cdot \cos 36^{\circ} \\ = \frac{1}{2} \cdot \frac{\sqrt{5} + 1}{4} \\ = \frac{\sqrt{5} + 1}{8} \end{aligned}$

Option (b) $\frac{\sqrt{5} - 1}{8}$ : This option is incorrect because the given expression $\cos^{2} 48^{\circ} - \sin^{2} 12^{\circ}$ simplifies to $\frac{\sqrt{5} + 1}{8}$ , not $\frac{\sqrt{5} - 1}{8}$ . The value $\frac{\sqrt{5} - 1}{8}$ does not match the derived result.
Option (c) $\frac{\sqrt{5} + 1}{5}$ : This option is incorrect because the denominator is 5 instead of 8. The correct simplification of the given expression results in $\frac{\sqrt{5} + 1}{8}$ , not $\frac{\sqrt{5} + 1}{5}$ .
Option (d) $\frac{\sqrt{5} + 1}{2 \sqrt{2}}$ : This option is incorrect because the denominator is $2 \sqrt{2}$ instead of 8. The correct simplification of the given expression results in $\frac{\sqrt{5} + 1}{8}$ , not $\frac{\sqrt{5} + 1}{2 \sqrt{2}}$ .

57. If $\tan α = \frac{1}{7}$ and $\tan β = \frac{1}{3}$ , then $\cos 2 α$ is equal to

(a) $\sin 2 β$

(b) $\sin 4 β$

(d) $\cos 2 β$

Show Answer

Thinking Process

Use $\cos 2 α = \frac{1 - \tan^{2} α}{1 + \tan^{2} α}$ and $\sin 2 α = \frac{2 \tan α}{1 + \tan^{2} α}$

Solution

(b) Given that,

$\begin{aligned} \cos 2 α & = \frac{1 - \frac{1}{49}}{1 + \frac{1}{49}} = \frac{\frac{48}{49}}{\frac{50}{49}} \\ = \frac{48}{50} = \frac{24}{25} \\ \Rightarrow \cos 2 α & = \frac{24}{25} . . (i) \\ We know that, \sin 4 β & = \frac{2 \tan 2 β}{1 + \tan^{2} 2 β} . . (i i) \\ and \tan 2 β & = \frac{2 \tan^{2}}{1 - \tan^{2} β} = \frac{2 \times \frac{1}{3}}{1 - \frac{1}{9}} \\ = \frac{2}{\frac{3}{9}} = \frac{2 \times 9}{3 \times 8} = \frac{3}{4} \end{aligned}$

$\tan = \frac{1}{7} and \tan β = \frac{1}{3}$

From Eq, (ii),

$\sin 4 β = \frac{2 \times \frac{3}{4}}{1 + \frac{9}{16}} = \frac{\frac{6}{4}}{\frac{25}{16}} = \frac{6 \times 16}{4 \times 25}$

$\Rightarrow \sin 4 β = \frac{24}{25}$

$\Rightarrow \sin 4 β = \cos 2 α$

$∴ \cos 2 α = \sin 4 β$

Option (a) $\sin 2 β$ : This option is incorrect because $\sin 2 β$ is not equal to $\cos 2 α$ . The correct relationship is derived from the double-angle formula for sine, which is $\sin 2 β = \frac{2 \tan β}{1 + \tan^{2} β}$ . Given $\tan β = \frac{1}{3}$ , $\sin 2 β$ would be $\frac{2 \times \frac{1}{3}}{1 + {(\frac{1}{3})}^{2}} = \frac{\frac{2}{3}}{1 + \frac{1}{9}} = \frac{\frac{2}{3}}{\frac{10}{9}} = \frac{2}{3} \times \frac{9}{10} = \frac{3}{5}$ , which is not equal to $\cos 2 α = \frac{24}{25}$ .
Option (c) $\sin 3 β$ : This option is incorrect because $\sin 3 β$ is not equal to $\cos 2 α$ . The triple-angle formula for sine is $\sin 3 β = 3 \sin β - 4 \sin^{3} β$ . Given $\tan β = \frac{1}{3}$ , we can find $\sin β$ using $\sin β = \frac{\tan β}{\sqrt{1 + \tan^{2} β}} = \frac{\frac{1}{3}}{\sqrt{1 + {(\frac{1}{3})}^{2}}} = \frac{\frac{1}{3}}{\sqrt{\frac{10}{9}}} = \frac{1}{3} \times \frac{3}{\sqrt{10}} = \frac{1}{\sqrt{10}}$ . Therefore, $\sin 3 β = 3 \times \frac{1}{\sqrt{10}} - 4 {(\frac{1}{\sqrt{10}})}^{3} = \frac{3}{\sqrt{10}} - \frac{4}{10 \sqrt{10}} = \frac{3}{\sqrt{10}} - \frac{2}{5 \sqrt{10}} = \frac{15 - 2}{5 \sqrt{10}} = \frac{13}{5 \sqrt{10}}$ , which is not equal to $\cos 2 α = \frac{24}{25}$ .
Option (d) $\cos 2 β$ : This option is incorrect because $\cos 2 β$ is not equal to $\cos 2 α$ . The double-angle formula for cosine is $\cos 2 β = \frac{1 - \tan^{2} β}{1 + \tan^{2} β}$ . Given $\tan β = \frac{1}{3}$ , $\cos 2 β = \frac{1 - {(\frac{1}{3})}^{2}}{1 + {(\frac{1}{3})}^{2}} = \frac{1 - \frac{1}{9}}{1 + \frac{1}{9}} = \frac{\frac{8}{9}}{\frac{10}{9}} = \frac{8}{10} = \frac{4}{5}$ , which is not equal to $\cos 2 α = \frac{24}{25}$ .

58. If $\tan θ = \frac{a}{b^{'}}$ , then $b \cos 2 θ + a \sin 2 θ$ is equal to

(a) a

(b) $b$

(d) None of these

Show Answer

Solution

(b) Given that, $\tan θ = \frac{a}{b}$

$\begin{aligned} ∴ b \cos 2 θ + a \sin 2 θ & = b (\frac{1 - \tan^{2} θ}{1 + \tan^{2} θ}) + a (\frac{2 \tan θ}{1 + \tan^{2} θ}) \\ = b (\frac{1 - \frac{a^{2}}{b^{2}}}{1 + \frac{a^{2}}{b^{2}}}) + a (\frac{\frac{2 a}{b}}{1 + \frac{a^{2}}{b^{2}}}) \\ = b (\frac{b^{2} - a^{2}}{b^{2} + a^{2}}) + \frac{2 a^{2} b}{a^{2} + b^{2}} \\ = \frac{b}{a^{2} + b^{2}} [b^{2} - a^{2} + 2 a^{2}] = \frac{(a^{2} + b^{2}) b}{(a^{2} + b^{2})} \\ = b \end{aligned}$

Option (a): a
This option is incorrect because the expression ( b \cos 2\theta + a \sin 2\theta ) simplifies to ( b ) and not ( a ). The derivation shows that the terms involving ( a ) and ( b ) combine in such a way that the final result is ( b ).
Option (c): (\frac{a}{b})
This option is incorrect because the expression ( b \cos 2\theta + a \sin 2\theta ) does not simplify to (\frac{a}{b}). The derivation clearly shows that the final result is ( b ), and there is no division by ( b ) that would result in (\frac{a}{b}).
Option (d): None of these
This option is incorrect because the correct answer is indeed one of the given options, specifically option (b). The derivation confirms that ( b \cos 2\theta + a \sin 2\theta ) simplifies to ( b ), making option (d) incorrect.

59. If for real values of $x, \cos θ = x + \frac{1}{x}$ , then

(a) $θ$ is an acute angle

(b) $θ$ is right angle

(d) No value of $θ$ is possible

Show Answer

Thinking Process

The quadratic equation $a x^{2} + b x + c = 0$ has real roots, then $b^{2} - 4 a c = 0$ , use this condition to solve the above problem.

Solution

(d)

$\begin{aligned} Here, \cos θ & = x + \frac{1}{x} \\ \Rightarrow \cos θ & = \frac{x^{2} + 1}{x} \\ x^{2} - x \cos θ + 1 & = 0 \end{aligned}$

For real value of $x, (- \cos θ)^{2} - 4 \times 1 \times 1 = 0$

$\begin{aligned} \cos^{2} θ & = 4 \\ \cos θ & = \pm 2 \end{aligned}$

which is not possible.

$[∵ - 1 \leq \cos θ \leq 1]$

(a) $θ$ is an acute angle: This option is incorrect because for $θ$ to be an acute angle, $\cos θ$ must lie within the range $0 < \cos θ \leq 1$ . However, the given equation $\cos θ = x + \frac{1}{x}$ leads to $\cos θ = \pm 2$ , which is outside the valid range for $\cos θ$ .
(b) $θ$ is right angle: This option is incorrect because for $θ$ to be a right angle, $\cos θ$ must be $0$ . The given equation $\cos θ = x + \frac{1}{x}$ does not yield $\cos θ = 0$ for any real value of $x$ .
(c) $θ$ is an obtuse angle: This option is incorrect because for $θ$ to be an obtuse angle, $\cos θ$ must lie within the range $- 1 \leq \cos θ < 0$ . However, the given equation $\cos θ = x + \frac{1}{x}$ leads to $\cos θ = \pm 2$ , which is outside the valid range for $\cos θ$ .

Fillers

60. The value of $\frac{\sin 50^{\circ}}{\sin 130^{\circ}}$ is ……

Show Answer

Solution

Here,

$\begin{aligned} \frac{\sin 50^{\circ}}{\sin 130^{\circ}} & = \frac{\sin (180^{\circ} - 130^{\circ})}{\sin 130^{\circ}} \\ = \frac{\sin 130^{\circ}}{\sin 130^{\circ}} = 1 \end{aligned}$

61. If $k = \sin (\frac{π}{18}) \sin (\frac{5 π}{18}) \sin (\frac{7 π}{18})$ , then the numerical value of $k$ is ……

Show Answer

Solution Here, $k = \sin (\frac{π}{18}) \sin (\frac{5 π}{18}) \sin (\frac{7 π}{18})$

$= \sin 10^{\circ} \sin 50^{\circ} \sin 70^{\circ}$

$\begin{aligned} = \sin 10^{\circ} \cos 40^{\circ} \cdot \cos 20^{\circ} \\ = \frac{1}{2} \sin 10^{\circ} [2 \cos 40^{\circ} \cdot \cos 20^{\circ}] \\ = \frac{1}{2} \sin 10^{\circ} [\cos 60^{\circ} + \cos 20^{\circ}] [∵ 2 \cos x \cdot \cos y = \cos (x + y) + \cos (x - y)] \\ = \frac{1}{2} \sin 10^{\circ} \cdot \frac{1}{2} + \frac{1}{2} \sin 10^{\circ} \cos 20^{\circ} \\ = \frac{1}{4} \sin 10^{\circ} + \frac{1}{4} [\sin 30^{\circ} - \sin 10^{\circ}] \\ = \frac{1}{8} \end{aligned}$

62. If $\tan A = \frac{1 - \cos θ}{\sin B}$ , then $\tan 2 A =$ ……

Show Answer

Thinking Process

Use $\cos θ = 1 - 2 \sin^{2} \frac{θ}{2}$ and $\tan 2 θ = \frac{2 \tan θ}{1 - \tan^{2} θ}$ .

Solution

Given that,

$\begin{aligned} \tan A & = \frac{1 - \cos B}{\sin B} \\ = \frac{1 - 1 + 2 \sin^{2} \frac{B}{2}}{2 \sin \frac{B}{2} \cdot \cos \frac{B}{2}} = \tan \frac{B}{2} \end{aligned}$

$Now, \tan 2 A = \frac{2 \tan A}{1 - \tan^{2} A}$

$\Rightarrow \tan 2 A = \frac{2 \cdot \tan \frac{B}{2}}{1 - \tan^{2} \frac{B}{2}}$

$\Rightarrow \tan 2 A = \tan B$

63. If $\sin x + \cos x = a$ , then

(i) $\sin^{6} x + \cos^{6} x = \dots \dots .$

(ii) $| \sin x - \cos x | = \dots \dots$

Show Answer

Solution

Given that, $\sin x + \cos x = a$

On squaring both sides, we get

$\begin{aligned} (\sin x + \cos x)^{2} = (a)^{2} \\ \Rightarrow \sin^{2} x + \cos^{2} x + 2 \sin x \cos x = a^{2} \\ \Rightarrow \sin x \cdot \cos x = \frac{1}{2} (a^{2} - 1) \\ (i) & \sin^{6} x + \cos^{6} x = (s i n^{2} x)^{3} + (\cos^{2} x)^{3} \\ = (\sin^{2} x + \cos^{2} x) (\sin^{4} x - \sin^{2} x \cos^{2} x + \cos^{4} x) \\ = \sin^{4} x + \cos^{4} x - \frac{1}{4} (a^{2} - 1)^{2} \\ = (\sin^{2} x + \cos^{2} x)^{2} - 2 \sin^{2} x \cos^{2} x - \frac{1}{4} (a^{2} - 1)^{2} \\ = 1 - 2 \cdot \frac{1}{4} (a^{2} - 1)^{2} - \frac{1}{4} (a^{2} - 1)^{2} = \frac{1}{4} [4 - 3 (a^{2} - 1)^{2}] \end{aligned}$

(ii) $| \sin x - \cos x | = \sqrt{(\sin x - \cos x)^{2}}$

$\begin{aligned} = \sqrt{\sin^{2} x + \cos^{2} x - 2 \sin x \cos x} \\ = \sqrt{1 - 2 \frac{1}{2} (a^{2} - 1)} = \sqrt{1 - a^{2} + 1} = \sqrt{2 - a^{2}} \end{aligned}$

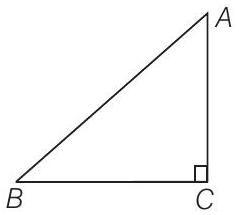
64. In right angled $△ A B C$ with $∠ C = 90^{\circ}$ the equation whose roots $a r e \tan A$ and $\tan B$ is ……

Show Answer

Solution

In right angled $△ A B C, ∠ C = 90^{\circ}$

$\begin{aligned} ∴ \tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} \\ \Rightarrow \frac{1}{0} = \frac{\tan A + \tan B}{1 - \tan A \tan B} \\ \Rightarrow \tan A \tan B = 1 \\ \tan A + \tan B = \frac{\sin A}{\cos A} + \frac{\sin B}{\cos B} \\ = \frac{\sin A}{\cos A} + \frac{\cos A}{\sin A} \\ = \frac{\sin^{2} A + \cos^{2} A}{\sin A \cdot \cos A} \\ = \frac{1}{\sin A \cdot \cos A} = \frac{2}{2 \cdot \sin A \cdot \cos A} \end{aligned}$

$\begin{matrix} = \frac{\sin A}{\cos A} + \frac{\sin (90^{\circ} - A)}{\cos (90^{\circ} - A)} & [∵ ∠ C = 90^{\circ}, ∠ B = 90^{\circ} - A] \\ = \frac{\sin A}{\cos A} + \frac{\cos A}{\sin A} \\ = \frac{\sin^{2} A + \cos^{2} A}{\sin A \cdot \cos A} \\ = \frac{1}{\sin A \cdot \cos A} = \frac{2}{2 \cdot \sin A \cdot \cos A} \\ = \frac{2}{\sin 2 A} & [∵ \sin 2 x = 2 \sin x \cos x] \end{matrix}$

So, the required equation is $x^{2} - \frac{2}{\sin A} x + 1$ .

$∵ \sin 2 x = 2 \sin x \cos x$

65. $3 (\sin x - \cos x)^{4} + 6 (\sin x + \cos x)^{2} + 4 (\sin^{6} x + \cos^{6} x) =$ ……

Show Answer

Thinking Process

Use formulae i.e., $(a^{3} + b^{3}) = (a + b) (a^{2} - a b + b^{2})$ and $a^{2} + b^{2} = (a + b)^{2} - 2 a b$ .

Solution

Given expression, $3 (\sin x - \cos x)^{4} + 6 (\sin x + \cos x)^{2} + 4 (\sin^{6} x + \cos^{6} x)$

$\begin{aligned} = 3 [\sin^{2} x + \cos^{2} x - 2 \sin x \cos x]^{2} + 6 [\sin^{2} x + \cos^{2} x + 2 \cdot \sin x \cdot \cos x] \\ + 4 [(\sin^{2} x)^{3} + (\cos^{2} x)^{3}] \\ = 3 (1 - \sin 2 x)^{2} + 6 (1 + \sin 2 x) + 4 [(\sin^{2} + \cos^{2} x) (\sin^{4} x - \sin x \cos^{2} x + \cos^{4} x) . \\ = 3 (1 + \sin^{2} 23 x - 2 \sin 2 x) + 6 + 6 \sin 2 x + 4 [(\sin^{2} x + \cos^{2} x)^{2} 3 \sin x \cos^{2} x] \\ = 3 + 3 \sin^{2} 2 x - 6 \sin 2 x + 6 + 6 \sin 2 x \\ = 4 - 3 \sin^{2} 2 x = 13 \end{aligned}$

66. Given $x > 0$ , the value of $f (x) = - 3 \cos \sqrt{3 + x + x^{2}}$ lie in the interval ……

Show Answer

Solution

Given function, $f (x) = - 3 \cos \sqrt{3 + x + x^{2}}$

$\begin{matrix} We know that, & - 1 \leq \cos x \leq 1 \\ \Rightarrow & - 3 \leq 3 \cos x \leq 3 \\ \Rightarrow & 3 \geq - 3 \cos x \geq - \\ \Rightarrow & - 3 \leq - 3 \cos x \leq 3 \end{matrix}$

So, the value of $f (x)$ lies in $[- 3, 3]$ .

67. The maximum distance of a point on the graph of the function $y = \sqrt{3} \sin x + \cos x$ from $X$ -axis is ……

Show Answer

Solution

Given that, $y = \sqrt{3} \sin x + \cos x$

$\begin{aligned} y & = 2 [\frac{\sqrt{3}}{2} \sin x + \frac{1}{2} \cos x] \\ = 2 [\sin x \cdot \cos \frac{π}{6} + \cos x \sin \frac{π}{6}] \\ = 2 \sin (x + π / 6) \end{aligned}$

Graph of $y = 2 \sin x$

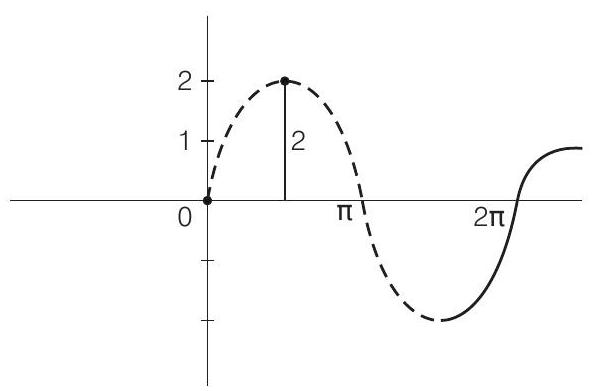
Hence, the maximum distance is 2 units.

True/False

68. In each of the questions 68 to 75 , state whether the statements is True or False? Also, give justification.

Show Answer

Thinking Process

$If \tan A = \frac{1 - \cos B}{\sin B}, then \tan 2 A = \tan B$

Solution

True

$\begin{aligned} Given that, & \tan A = \frac{1 - \cos B}{\sin B} = \frac{1 - 1 + 2 \sin^{2} \frac{B}{2}}{2 \sin \frac{B}{2} \cdot \cos \frac{B}{2}} = \tan \frac{B}{2} \\ Now, & \tan 2 A = \frac{2 \tan A}{1 - \tan^{2} A} = \frac{2 \cdot \tan \frac{B}{2}}{1 - \tan^{2} \frac{B}{2}} = \tan B \end{aligned}$

69. The equality $\sin A + \sin 2 A + \sin 3 A = 3$ holds for some real value of $A$ .

Show Answer

Solution

False

Given that, $\sin A + \sin 2 A + \sin 3 A = 3$

It is possible only if $\sin A, \sin 2 A, \sin 3 A$ each has a value one because maximum value of $\sin A$ is a certain angle is 1 . Which is not possible because angle are different.

70. $\sin 10^{\circ}$ is greater than $\cos 10^{\circ}$ .

Show Answer

Solution

False

$\sin 10^{\circ} = \sin (90^{\circ} - 80^{\circ})$

$\sin 10^{\circ} = \cos 80^{\circ}$

$∵ \cos 80^{\circ} < \cos 10^{\circ}$

$Hence, \sin 10^{\circ} < \cos 10^{\circ}$

71. $\cos \frac{2 π}{15} \cos \frac{4 π}{15} \cos \frac{8 π}{15} \cos \frac{16 π}{15} = \frac{1}{16}$

Show Answer

Solution

True

$\begin{aligned} LHS & = \cos \frac{2 π}{15} \cos \frac{4 π}{15} \cos \frac{8 π}{15} \cos \frac{16 π}{15} \\ = \cos 24^{\circ} \cos 48^{\circ} \cos 96^{\circ} \cos 192^{\circ} \\ = \frac{1}{16 \sin 24^{\circ}} [(2 \sin 24^{\circ} \cos 24^{\circ}) (2 \cos 48^{\circ}) (2 \cos 96^{\circ}) (2 \cos 192^{\circ})] \\ = \frac{1}{16 \sin 24^{\circ}} [2 \sin 48^{\circ} \cos 48^{\circ} (2 \cos 96^{\circ}) (2 \cos 192^{\circ})] \\ = \frac{1}{16 \sin 24^{\circ}} [(2 \sin 96^{\circ} \cos 96^{\circ}) (2 \cos 192^{\circ})] \\ = \frac{1}{16 \sin 24^{\circ}} [2 \sin 192^{\circ} \cos 192^{\circ}) \\ = \frac{1}{16 \sin 24^{\circ}} \sin 384^{\circ} = \frac{\sin (360^{\circ} + 24^{\circ})}{16 \sin 24^{\circ}} \\ = \frac{1}{16} = R H S Hence proved. \end{aligned}$

72. One value of $θ$ which satisfies the equation $\sin^{4} θ - 2 \sin^{2} θ - 1$ lies between 0 and $2 π$ .

Show Answer

Solution

False

Given equation, $\sin^{4} θ - 2 \sin^{2} θ - 1 = 0$

$\Rightarrow \sin^{2} θ = \frac{2 \pm \sqrt{4 + 4}}{2}$

$\Rightarrow \sin^{2} θ = \frac{2 \pm 2 \sqrt{2}}{2}$

$\Rightarrow \sin^{2} θ = (1 + \sqrt{2})$ or $(1 - \sqrt{2}) \Rightarrow - 1 \leq \sin θ \leq 1$

$\Rightarrow \sin^{2} θ \leq 1$

$∵ \sin^{2} θ = \sqrt{2 + 1}$ or $(1 - \sqrt{2})$

which is not possible.

73. If $c o s e c x = 1 + \cot x$ , then $x = 2 n π, 2 n π + \frac{π}{2}$

Show Answer

Solution

True

Given that,

$\begin{aligned} c o s e c x & = 1 + \cot x \\ \frac{1}{\sin x} & = 1 + \frac{\cos x}{\sin x} \Rightarrow \frac{1}{\sin x} = \frac{\sin x + \cos x}{\sin x} \end{aligned}$

$\Rightarrow$

$\Rightarrow \sin x + \cos x = 1$

$\Rightarrow \frac{1}{\sqrt{2}} \cdot \sin x + \frac{1}{\sqrt{2}} \cdot \cos x = \frac{1}{\sqrt{2}}$

$\Rightarrow \sin \frac{π}{4} \sin x + \cos x \cos \frac{π}{4} = \frac{1}{\sqrt{2}}$

$\Rightarrow \cos (x - \frac{π}{4}) = \cos \frac{π}{4}$

$∴ x - \frac{π}{4} = 2 n π \pm \frac{π}{4}$

$\begin{aligned} For positive sign, & x = 2 n π + \frac{π}{4} + \frac{π}{4} = 2 n π + \frac{π}{2} \\ For negative sign, & x = 2 n π - \frac{π}{4} + \frac{π}{4} = 2 n π \end{aligned}$

74. If $\tan θ + \tan 2 θ + \sqrt{3} \tan θ \tan 2 θ = \sqrt{3}$ , then $θ = \frac{n π}{3} + \frac{π}{9}$ .

Show Answer

Solution

True

$\begin{aligned} \tan θ + \tan 2 θ + \sqrt{3} \tan θ \tan 2 θ = \sqrt{3} \\ \Rightarrow \tan θ + \tan 2 θ = \sqrt{3} - \sqrt{3} \tan θ \tan 2 θ \\ \Rightarrow \tan θ + \tan 2 θ = \sqrt{3} (1 - \tan θ \tan 2 θ) \\ \Rightarrow \frac{\tan θ + \tan 2 θ}{1 - \tan θ \tan 2 θ} = \sqrt{3} \\ \Rightarrow \tan (θ + 2 θ) = \tan \frac{π}{3} \Rightarrow \tan 3 θ = \tan \frac{π}{3} \\ ∴ 3 θ = n π + \frac{π}{3} \\ θ = \frac{n π}{3} + \frac{π}{9} \end{aligned}$

75. If $\tan (π \cos θ) = \cot (π \sin θ)$ , then $\cos θ - \frac{π}{4} = \pm \frac{1}{2 \sqrt{2}}$ .

Show Answer

Thinking Process

Use the formulae i.e., $\tan \frac{π}{2} - θ = \cot θ$ and $\cos (A - B) = \cos A \cos B + \sin A \sin B$ .

Solution

True

$We have, \tan (π \cos θ) = \cot (π \sin θ)$

$\Rightarrow \tan (π \cos θ) = \tan \frac{π}{2} - (π \sin θ)$

$\Rightarrow π \cos = \frac{π}{2} - π \sin θ$

$\Rightarrow π (\sin θ + \cos θ) = \frac{π}{2}$

$\Rightarrow \sin θ + \cos θ = \frac{1}{2}$

$\Rightarrow \frac{1}{\sqrt{2}} \cdot \sin θ + \frac{1}{\sqrt{2}} \cdot \cos θ = \frac{1}{2 \sqrt{2}}$

$\Rightarrow \sin θ \cdot \sin \frac{π}{4} + \cos θ \cdot \cos \frac{π}{4} = \frac{1}{2 \sqrt{2}}$

$∴ \cos θ - \frac{π}{4} = \frac{1}{2 \sqrt{2}}$

76. In the following match each item given under the Column I to its correct answer given under the Column II.

	Column I		Column II
(i)	$\sin (x + y) \sin (x - y)$	(a)	$\cos^{2} x - \sin^{2} y$
(ii)	$\cos (x + y) \cos (x - y)$	(b)	$1 - \tan θ / 1 + \tan θ$
(iii)	$\cot (\frac{π}{4} + θ)$	(c)	$1 + \tan θ / 1 - \tan θ$
(iv)	$\tan (\frac{π}{4} + θ)$	(d)	$\sin^{2} x - \sin^{2} y$

Show Answer

Solution

(i) $\sin (x + y) \sin (x - y) = \sin^{2} x - \sin^{2} y$

(ii) $\cos (x + y) \cos (x - y) = \cos^{2} x - \sin^{2} y$

(iii) $\cot \frac{π}{4} + θ = \frac{\cot \frac{π}{4} \cot θ - 1}{\cot \frac{π}{4} + \cot θ}$

$= \frac{- 1 + \cot θ}{1 + \cot θ} = \frac{1 - \tan θ}{1 + \tan θ}$

(iv) $\tan \frac{π}{4} + θ = \frac{\tan \frac{π}{4} + \tan θ}{1 - \tan \frac{π}{4} \tan θ} = \frac{1 + \tan θ}{1 - \tan θ}$

Hence, the correct mathes are (i) $\rarr$ (d), (ii) $\rarr$ (a), (iii) $\rarr$ (b), (iv) $\rarr$ (c).

Relations and Functions

Trigonometric Functions

Short Answer Type Questions

Long Answer Type Questions

Objective Type Questions

Fillers

True/False

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Mentorship

NCERT Exercise Video Solution

Trigonometric Functions

Short Answer Type Questions

Long Answer Type Questions

Objective Type Questions

Fillers

True/False

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Mentorship

NCERT Exercise Video Solution

Menu