Straight Lines
Short Answer Type Questions
1. Find the equation of the straight line which passes through the point
Show Answer
Solution
Let the intercepts along the
Since, the point
On putting
2. Find the equation of the line passing through the point
Show Answer
Thinking Process
First of all find the slope, using the formula
Solution
Consider the given points
Slope of the line passing through the points
So, the slope of required line is
Since, the equation of a line passing the point
3. Find the angle between the lines
Show Answer
Thinking Process
If the angle between the lines having the slope
Use this formula to solve the above problem.
Solution
Let
For obtuse angle
Hence, the angle between the lines are
4. Find the equation of the lines which passes through the point
Show Answer
Solution
Let the intercept along the axes be
Given,
Now, the equation of line is
Since, the point
So, the equation of line, when
5. Find the points on the line
Show Answer
Thinking Process
The perpendicular distance of a point
Solution
Let the required point be
The distance of the point
Taking positive sign,
From Eq. (i)
So, the point is
Taking negative sign,
On putting
Hence, the required points are
6. Show that the tangent of an angle between the lines
Show Answer
Solution
Given equation of lines are
Let
Hence proved.
7. Find the equation of lines passing through
Show Answer
Thinking Process
Equation of a line passing through the point
Solution
Given that, angle with
and angle with
So, the equation of a line passing through
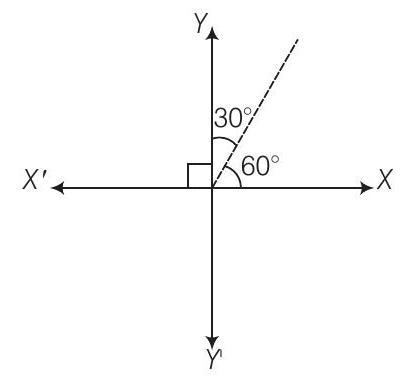
8. Find the equation of the line passing through the point of intersection of
Show Answer
Thinking Process
First of all solve the given equation of lines to get the point of intersection. Then, if a line having slope
Solution
Given equation of lines
From Eq. (i),
Now, put the value of
Now,
Since, the required line is parallel to the line
So, the equation of the line passing through the point
9. For what values of
Show Answer
Solution
Given equation of line
So, the intercepts are
and another given equation of line is
So, the intercepts are -3 and 2 .
According to the question,
10. If the intercept of a line between the coordinate axes is divided by the point
Show Answer
Thinking Process
The coordinates of a point which divides the join of
Solution
Let intercept of a line are
The coordinates of
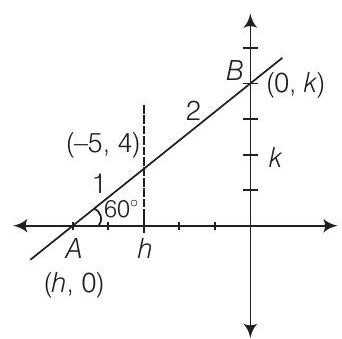
Hence, the equation of a line
11. Find the equation of a straight line on which length of perpendicular from the origin is four units and the line makes an angle of
Show Answer
Thinking Process
The equation of the line having normal distance Pfrom the origin and angle
Solution
Given that,
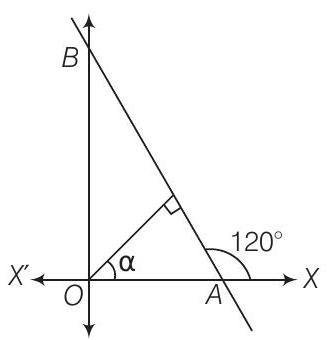
12. Find the equation of one of the sides of an isosceles right angled triangle whose hypotenuse is given by
Show Answer
Solution
Let slope of line
Taking negative sign,
Long Answer Type Questions
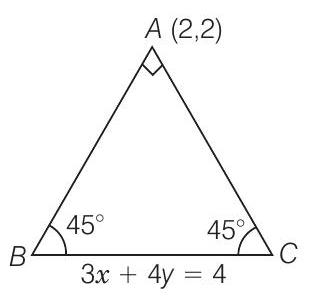
13. If the equation of the base of an equilateral triangle is
Show Answer
Thinking Process
Find the length of perpendicular (
Solution
Given that, equilateral
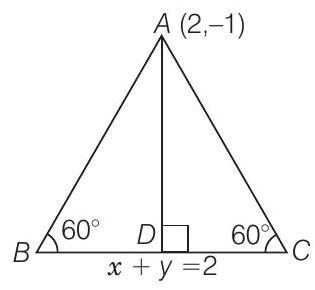
Now, the length of perpendicular from
From Eq. (i),
14. A variable line passes through a fixed point
Show Answer
Thinking Process
Let the slope of the line be
Solution
Let slope of the line be
Since, the given points are
Now, perpendicular distance from
Perpendicular distance from
Perpendicular distance from
Since,
15. In what direction should a line be drawn through the point
Show Answer
Solution
Let slope of the line be
and
So, the point of intersection is
16. A straight line moves so that the sum of the reciprocals of its intercepts made on axes is constant. Show that the line passes through a fixed point.
Show Answer
Thinking Process
If a line is
Solution
Since, the intercept form of a line is
Given that,
So,
Hence, the line passes through the fixed point.
17. Find the equation of the line which passes through the point
Show Answer
Thinking Process
If the point
Solution
Since, the line intersects
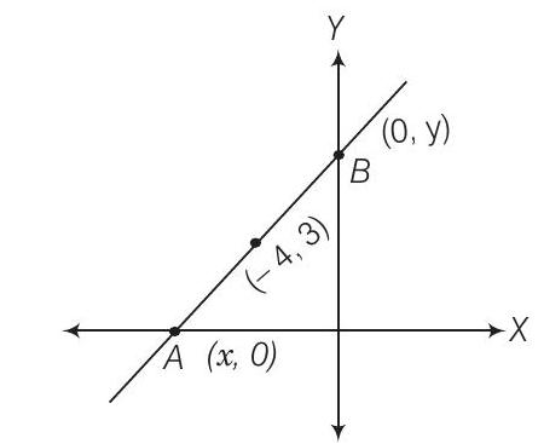
Since, the intercept on the
18. Find the equations of the lines through the point of intersection of the lines
Show Answer
Solution
Given equation of lines
Now, put the value of
Since, the point of intersection is
Let slope of the required line be
Since, the distance from
19. If the sum of the distance of a moving point in a plane from the axes is 1 , then find the locus of the point.
Show Answer
Thinking Process
Given that
Solution
Let the coordinates of moving point
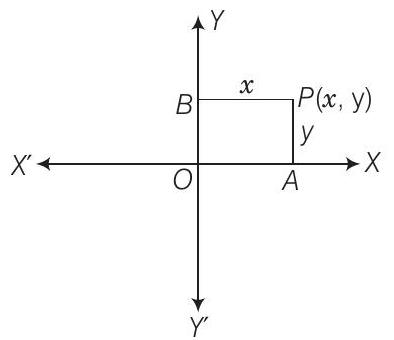
So, these equations give us locus of the point which is a square.
20.
Show Answer
Thinking Process
Lines are
Solution
Given equation of lines are
On putting
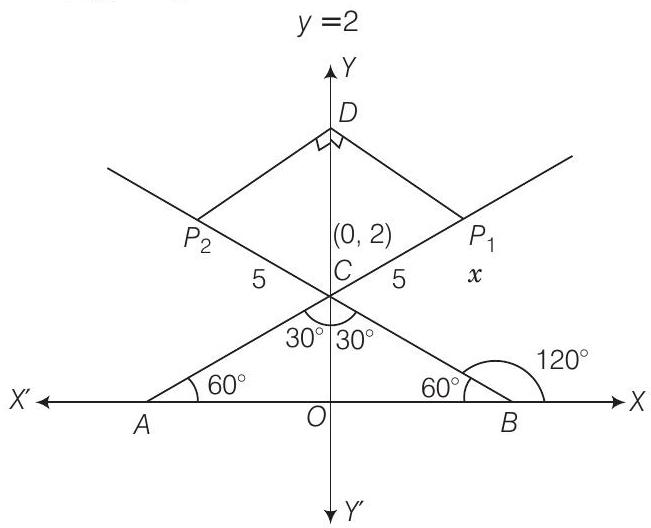
So, the point of intersection of line (i) and (ii) is
Here,
So, the coordinates of the foot of perpendiculars are
21. If
Show Answer
Solution
Given equation of line is,
Perpendicular length from the origin on the line (i) is given by
Given that,
Objective Type Questions
22. A line cutting off intercept -3 from the
(a)
(b)
(c)
(d) None of the above
Show Answer
Solution
(a) Given that,
- Option (b)
- Option (c)
23. Slope of a line which cuts off intercepts of equal lengths on the axes is
(a) -1
(b) 0
(c) 2
(d)
Show Answer
Solution
(a) Let equation of line be
-
Option (b) 0: The slope of 0 would imply a horizontal line, which does not cut off intercepts of equal lengths on the axes. A horizontal line would only intersect the y-axis and not the x-axis.
-
Option (c) 2: A slope of 2 would imply a steep line that does not cut off intercepts of equal lengths on the axes. The intercepts would not be symmetric and equal in length.
-
Option (d)
24. The equation of the straight line passing through the point
(a)
(b)
(c)
(d)
Show Answer
Solution
(b) Since, line passes through the point
-
Option (a)
-
Option (c)
-
Option (d)
25. The equation of the line passing through the point
(a)
(b)
(c)
(d)
Show Answer
Solution
(b) Given point is
-
Option (a)
-
Option (c)
-
Option (d)
26. The tangent of angle between the lines whose intercepts on the axes are
(a)
(b)
(c)
(d) None of these
Show Answer
Solution
(c) Since, intercepts on the axes are
So, the lope of this line i.e.,
Also, for intercepts on the axes as
and slope of this line i.e.,
-
Option (a): The expression (\frac{a^{2}-b^{2}}{a b}) does not account for the factor of 2 in the denominator that arises from the formula for the tangent of the angle between two lines. The correct formula involves dividing by 2, which is missing in this option.
-
Option (b): The expression (\frac{b^{2}-a^{2}}{2}) is incorrect because it does not include the product of (a) and (b) in the denominator. The correct formula for the tangent of the angle between the lines should have (2ab) in the denominator, not just 2.
-
Option (d): This option is incorrect because the correct answer is provided in option (c). Therefore, “None of these” is not a valid choice.
27. If the line
(a)
(b)
(c)
(d)
Show Answer
Solution
(d) Given, line is
Since, the points
On multiplying by 2 in Eq. (ii) and then subtracting Eq. (iii) from Eq. (ii), we get
On putting
-
Option (a)
- For ((2, -3)): (2 + (-3) = -1 \neq 1)
- For ((4, -5)): (4 + (-5) = -1 \neq 1) Therefore, the points do not lie on the line (x + y = 1).
-
Option (b)
- For ((2, -3)): (-2 + (-3) = -5 \neq 1)
- For ((4, -5)): (-4 + (-5) = -9 \neq 1) Therefore, the points do not lie on the line (-x + y = 1).
-
Option (c)
- For ((2, -3)): (2 - (-3) = 5 \neq 1)
- For ((4, -5)): (4 - (-5) = 9 \neq 1) Therefore, the points do not lie on the line (x - y = 1).
28. The distance of the point of intersection of the lines
(a)
(b)
(c)
(d) None of these
Show Answer
Thinking Process
First of all find the point of intersection of the given first two lines, then get the perpendicular distance from this point to the third line. Using formula i.e., distance of a point
Solution
(a) Given equation of lines
and
From Eq. (ii), put the value of
From Eq. (ii),
So, the point of intersection is
-
Option (b): The numerator in the distance formula is incorrectly calculated. The correct numerator should be 130, not 13. This option likely results from a miscalculation or simplification error.
-
Option (c): The denominator in the distance formula is incorrectly simplified. The correct denominator should include the term (\sqrt{29}), not just 7. This option likely results from an incorrect application of the distance formula.
-
Option (d): This option is a catch-all for any answer that does not match the correct calculation. Since option (a) is correct, option (d) is not applicable.
29. The equation of the lines which pass through the point
(a)
(b)
(c)
(d) None of the above
Show Answer
Solution
(a) So, the given point
So, the equation of line
Let slope of the required line be
So, the required equation of lines are
-
Option (b): The equation
-
Option (c): This option only provides one of the correct lines,
30. The equations of the lines passing through the point
(a)
(b)
(c)
(d) None of the above
Show Answer
Solution
(a) Let slope of the line be
Since, the distance from origin is
Then,
So, the first equation of line is
and the second equation of line is
-
Option (b) is incorrect because the signs of the constant terms in the equations do not match the derived equations. The correct equations should have negative constants, not positive.
-
Option (c) is incorrect because the coefficients of (x) and (y) are not in the correct ratio. The correct equations should have (\sqrt{3}) as the coefficient of (x) and (\pm 1) as the coefficient of (y), not (1) and (\pm \sqrt{3}).
-
Option (d) is incorrect because option (a) is correct, so “None of the above” cannot be the correct answer.
31. The distance between the lines
(a)
(b)
(c)
(d) 0
Show Answer
Solution
(b) Given, equation of the lines are and
-
Option (a) is incorrect because it does not take the absolute value of the difference between (c_1) and (c_2). The distance between two parallel lines should always be a positive quantity, hence the absolute value is necessary.
-
Option (c) is incorrect because it does not take the absolute value of the difference between (c_2) and (c_1). The distance between two parallel lines should always be a positive quantity, hence the absolute value is necessary.
-
Option (d) is incorrect because it suggests that the distance between the two lines is zero. This would only be true if (c_1 = c_2), but in general, (c_1) and (c_2) are different, leading to a non-zero distance.
32. The coordinates of the foot of perpendiculars from the point
(a)
(b)
(c)
(d)
Show Answer
Solution
(b) Given, equation of the line is
So, the slope of line
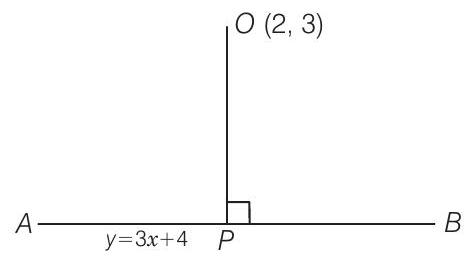
Using the value of
Put
So, the foot of perpendicular is
-
Option (a): The coordinates (\left(\frac{37}{10}, \frac{-1}{10}\right)) are incorrect because the x-coordinate should be (-\frac{1}{10}) and the y-coordinate should be (\frac{37}{10}) as derived from the calculations. This option has the coordinates swapped and the signs incorrect.
-
Option (c): The coordinates (\left(\frac{10}{37}, -10\right)) are incorrect because they do not satisfy the equations derived from the given line and the perpendicular line. The correct coordinates should be (\left(-\frac{1}{10}, \frac{37}{10}\right)).
-
Option (d): The coordinates (\left(\frac{2}{3}, -\frac{1}{3}\right)) are incorrect because they do not satisfy the equations derived from the given line and the perpendicular line. The correct coordinates should be (\left(-\frac{1}{10}, \frac{37}{10}\right)).
33. If the coordinates of the middle point of the portion of a line intercepted between the coordinate axes is
(a)
(b)
(c)
(d)
Show Answer
Solution
(a) Since, the coordinates of the middle point are
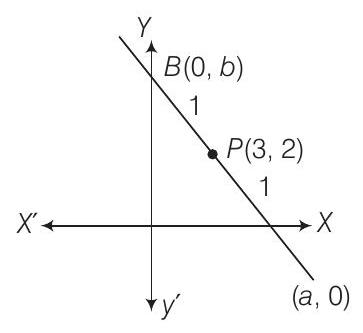
-
Option (b)
-
Option (c)
-
Option (d)
34. Equation of the line passing through
(a)
(b)
(c)
(d)
Show Answer
Solution
(c) Since, the line passes through
-
Option (a): The equation
-
Option (b): The equation
-
Option (d): The equation
35. Equations of diagonals of the square formed by the lines
(a)
(b)
(c)
(d)
Show Answer
Solution
(a) Equation of
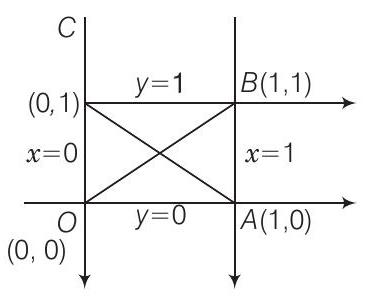
-
Option (b): The equation (x + y = 2) does not intersect the square formed by the lines (x = 0), (y = 0), (x = 1), and (y = 1). The correct equation for the diagonal should intersect at the vertices of the square, which are ((0,0)) and ((1,1)) for one diagonal, and ((0,1)) and ((1,0)) for the other.
-
Option (c): The equation (2y = x) does not represent a diagonal of the square. For a square with sides parallel to the axes, the diagonals should have slopes of (1) or (-1). Additionally, the equation (y + x = \frac{1}{3}) does not pass through any of the vertices of the square.
-
Option (d): The equation (y = 2x) does not represent a diagonal of the square. The slope of (2) is incorrect for the diagonals of a square with sides parallel to the axes. Similarly, the equation (y + 2x = 1) does not pass through any of the vertices of the square.
36. For specifying a straight line, how many geometrical parameters should be known?
(a) 1
(b) 2
(c) 4
(d) 3
Show Answer
Solution
(b) Equation of straight lines are
It is clear that from Eqs. (i), (ii), (iii) and (iv), for specifying a straight line clearly two parameters should be known.
-
Option (a) 1: Knowing only one parameter is insufficient to specify a straight line because a single parameter does not provide enough information to determine both the slope and the position of the line.
-
Option (c) 4: Knowing four parameters is excessive and unnecessary for specifying a straight line. A straight line in a plane can be fully described with just two parameters, such as the slope and y-intercept, or two points on the line.
-
Option (d) 3: Knowing three parameters is more than necessary to specify a straight line. While three parameters can describe a line, only two are needed to fully determine its characteristics. The third parameter would be redundant.
37. The point
(i) Reflection about the line
(ii) Translation through a distance 2 units along the positive
Then, the final coordinates of the point are
(a)
(b)
(c)
(d)
Show Answer
Solution
(b) Let the reflection of
Now, mid-point of
i.e.,
So, the slope of line
On putting
So, the point is
Hence, after translation the point is
-
Option (a)
-
Option (c)
-
Option (d)
38. A point equidistant from the lines
(a)
(b)
(c)
(d)
Show Answer
Solution
(c) The given equation of lines are
Let the point
Distance from line (i)
Distance from line (ii)
Distance from the line (iii)
So, the point
Clearly, if
Hence, the required point is
-
Option (a)
- Substituting
- Distance from line (i):
- Distance from line (ii):
- Distance from line (iii):
- Distance from line (i):
- The distances are not equal, so
- Substituting
-
Option (b)
- Substituting
- Distance from line (i):
- Distance from line (ii):
- Distance from line (iii):
- Distance from line (i):
- The distances are not equal, so
- Substituting
-
Option (d)
- Substituting
- Distance from line (i):
- Distance from line (ii):
- Distance from line (iii):
- Distance from line (i):
- The distances are not equal, so
- Substituting
39. A line passes through
(a)
(b)
(c) 1
(d)
Show Answer
Thinking Process
First of all find the equation of required line using the formulae. i.e.,
Solution
(d) Given line is
Then, slope of the required line
-
Option (a)
-
Option (b)
-
Option (c) 1 is incorrect because when solving for the y-intercept of the required line, substituting
40. The ratio in which the line
(a)
(b)
(c)
(d)
Show Answer
Solution
(b) Let point
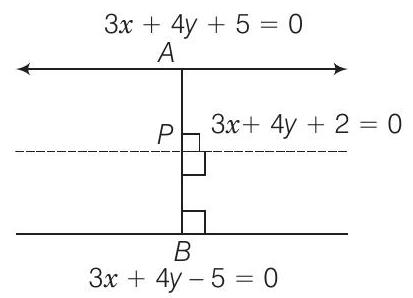
Now, perpendicular distance from
Let point
Hence, the required ratio is
-
Option (a) (1:2): This ratio is incorrect because the calculation of the perpendicular distances from the points on the lines (3x + 4y + 5 = 0) and (3x + 4y - 5 = 0) to the line (3x + 4y + 2 = 0) does not yield a ratio of (1:2). The correct distances are (\frac{7}{5}) and (\frac{3}{5}), which do not simplify to (1:2).
-
Option (c) (2:3): This ratio is incorrect because the perpendicular distances calculated from the points on the lines (3x + 4y + 5 = 0) and (3x + 4y - 5 = 0) to the line (3x + 4y + 2 = 0) do not result in a ratio of (2:3). The correct distances are (\frac{7}{5}) and (\frac{3}{5}), which do not simplify to (2:3).
-
Option (d) (2:5): This ratio is incorrect because the perpendicular distances from the points on the lines (3x + 4y + 5 = 0) and (3x + 4y - 5 = 0) to the line (3x + 4y + 2 = 0) do not yield a ratio of (2:5). The correct distances are (\frac{7}{5}) and (\frac{3}{5}), which do not simplify to (2:5).
41. One vertex of the equilateral triangle with centroid at the origin and one side as
(a)
(b)
(c)
(d)
Show Answer
Thinking Process
Let
Solution
(c) Let
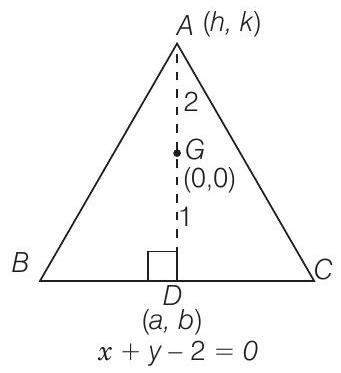
We know that,
Since, the slope of line
and slope of the line
From Eqs. (i) and (iii),
-
Option (a)
-
Option (b)
-
Option (d)
Fillers
42. If
Show Answer
Thinking Process
If
Solution
Given line is
Since,
On comparing Eqs. (i) and (ii), we get
So,
43. The line which cuts off equal intercept from the axes and pass through the point
Show Answer
Solution
Let equation of line is
Since, this line passes through
44. Equation of the line through thes point
Show Answer
Solution
Since, the given point
Slope of this line is
Let the slope of the required line is
Taking positive sign,
Taking negative sign,
and second equation of the line is
45. The points
Show Answer
Solution
For point
Since, the value are of opposite sign.
Hence, the points
46. A point moves so that square of its distance from the point
Show Answer
Solution
Let the coordinaters of the point are
Now, distance of the point
Given that,
47. Locus of the mid-points of the portion of the line
Show Answer
Solution
Given equation of the line is
Let the mid-point of
So, the mid-point of
Since, the point
and the point
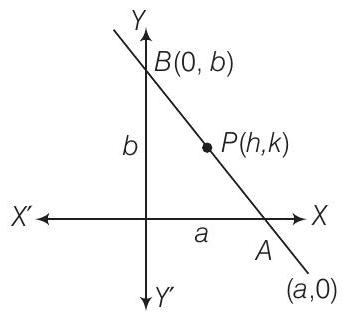
Now
and
Locus of the mid-point is
True/False
48. If the vertices of a triangle have integral coordinates, then the triangle cannot be equilateral.
Show Answer
Solution
True
We know that, if the vertices of a triangle have integral coordinates, then the triangle cannot be equilateral. Hence, the given statement is true.
Since, in equilatteral triangle, we get
49. The points
Show Answer
Solution
False
Given points are
Now,
Slope of
Slope of
Since, the slopes are different.
Hence,
50. Equation of the line passing through the point
Show Answer
Solution
False
Given point
and
Hence, the given statement is false.
51. The straight line
Show Answer
Solution
True
From Eq. (i), put the value of
So, the point of intersection is
If the line
So, this point lies on the given line.
Hence, the statement is true.
52. The vertex of an equilateral triangle is
Show Answer
Solution
True
Let
Let slope of line
Since, the angle between line
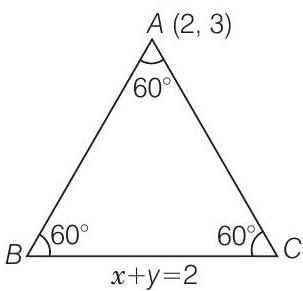
Similarly, slope of
[taking negative sign]
Hence, the statement is true.
53. The equation of the line joining the point
Show Answer
Thinking Process
Equation of a line passing through the points
Solution
True
Given equation of lines are
From Eq. (i), on putting
On putting
Now, the equation of a line passing through
Distance from
Hence, the statement is true.
54. The line
Show Answer
Solution
True
Given that, equation of line is
Equation of line passing through origin and perpendicular to line (i) is
Now, foot of perpendicular is the point of intersection of lines (i) and (ii). To find its locus we have to eliminate the variable
On squaring and adding Eqs. (i) and (ii), we get
Hence, the statement is true.
55. The lines
Show Answer
Thinking Process
First of all find the intersection point of first two line. Then, if the lines are concurrent then this point should lies on the third line.
Solution
False
Given lines are
and
From Eq. (i), on putting
Now, using
So, the point of intersection is
Since, this point lies on
Hence, the given statement is false.
56. Line joining the points
Show Answer
Solution
False
Given points are
Now
and
So, line
Matching The Columns
57. Match the following.
| Column I | Column II |
|---|---|
| (i)The coordinates of the points the line distance of 2 units from the line |
(a) |
| (ii)The coordinates of the point on the line from the line |
(b) |
| (iii)The coordinates of the point on the line joining |
(c) |
Show Answer
Solution
(i) Let the coordinate of point
(ii) Let coordinates of the point on the line
So, the point is
Similarly, taking negative sign the point is
(iii) Given point
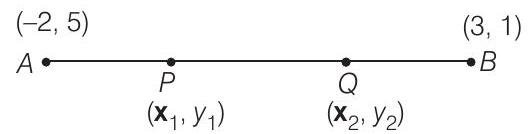
Now, the point
So, the coordinates of
Thus, the point
Hence, the coordinates of
Hence, the correct matches are (i)
58. The value of the
| Column I | Column II |
|---|---|
| (i) parallel to |
(a) |
| (ii) perpendicular to |
(b) |
| (iii) passes through |
(c) |
| (iv) parallel to |
(d) |
Show Answer
Solution
(i) Given equation of the line is
If line is parallel to
(ii) If the line (i) is perpendicular to the line
(iii) If the line (i) passes through the point
(iv) If the line is parallel to
So, the correct matches are (i)
59. The equation of the line through the intersection of the lines
| Column I | Column II |
|---|---|
| (i) through the point |
(a) |
| (ii) perpendicular to the line |
(b) |
| (iii) parallel to the line |
(c) |
| (iv) equally inclined to the axes is | (d) |
Show Answer
Solution
Given equation of the lines are
and
From Eq. (i), put
Now, put
So, the intersection points are
(i) The equation of the line passes through the point
(ii) If the required line is perpendicular to the line
(iii) If the required line is parallel to the line
(iv) If the line is equally inclined to the
| So, the correct matches are (a) |










