Sets
Short Answer Type Questions
1. Write the following sets in the roaster form.
(i)
(ii)
(iii)
Show Answer
Thinking Process
Solve the equation and get the value of
Solution
(i) We have,
(iii) We have,
Since, positive factors of a prime number are 1 and the number itself.
2. Write the following sets in the roaster form.
(i)
(ii)
(iii)
Show Answer
Thinking Process
Solve the given equation and get the value of respective variable.
Solution
(i) We have,
(ii)
(iii) We have,
Note in roaster form, the order in which elements are listed is immaterial. Thus, we can also write
3. If
Show Answer
Thinking Process
First, write all the factors of
Solution
4. State which of the following statements are true and which are false. Justify your answer.
(i)
(ii)
(iii)
(iv)
Show Answer
Solution
(i) Since, the factors of 35 are
(ii) Since, the factors of 128 are 1, 2, 4, 8, 16, 32, 64 and 128.
So, statement (ii) is false. (iii) We have,
which is not true.
Hence, statement (iii) is true.
(iv)
So, the factors of 496 are
So,
Hence, statement (iv) is false.
5. If
Show Answer
Solution
Given,
Now,
Hence,
6. If
(i)
(ii)
(iii)
Show Answer
Solution
(i) Let
Hence,
(ii) If
Let
But
From Eqs. (i) and (ii),
If
Let
Hence,
(iii) Let
Hence,
7. Given that
(i) the subset of
(ii) the subset of
Show Answer
Solution
We have,
(i) Required subset
(ii) Required subset
8. If
(i)
(ii)
(iii)
(iv)
Show Answer
Solution
Given,
(i)
(ii)
(iii)
(iv)
9. If
(i)
(ii)
(iii)
Show Answer
Solution
Given,
(i)
(ii)
(iii) is less than 6 and
10
Show Answer
Solution
11. Let
Show Answer
Solution
12. For all sets
Show Answer
Thinking Process
To prove this we have to show that
Solution
Let
Now, let
From Eqs. (i) and (ii),
13. For all sets
Show Answer
Thinking Process
To solve the above problem, use distributive law on sets
i.e.,
Solution
Hence, given statement is true.
14. For all sets
Show Answer
Solution
See the Venn diagrams given below, where shaded portions are representing
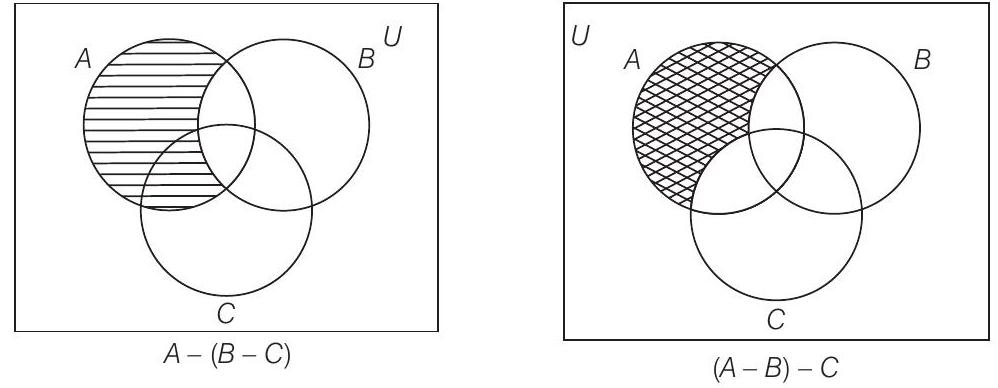
Clearly,
Hence, given statement is false.
15. For all sets
Show Answer
Solution
Let
Hence, given statement is true.
16. For all sets
Show Answer
Solution
Let
Hence, given statement is true.
17. For all sets
Show Answer
Solution
Let
Hence, given statement is true.
18. For all sets
Show Answer
Thinking Process
To solve the above problem, use distributive law i.e.,
Solution
19. For all sets
Show Answer
Solution
20. For all sets
Show Answer
Solution
21. For all sets
Show Answer
Solution
22. Let
Show Answer
Thinking Process
First of all solve the given equation and get the value of
Solution
Since
Hence,
Long Answer Type Questions
23. If
Show Answer
Solution
Let
Again, let
From Eqs. (i) and (ii)
24. Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science, 4 in English and Science, 4 in all the three. Find how many passed
(i) in English and Mathematics but not in Science.
(ii) in Mathematics and Science but not in English.
(iii) in Mathematics only.
(iv) in more than one subject only.
Show Answer
Solution
Let
Then,
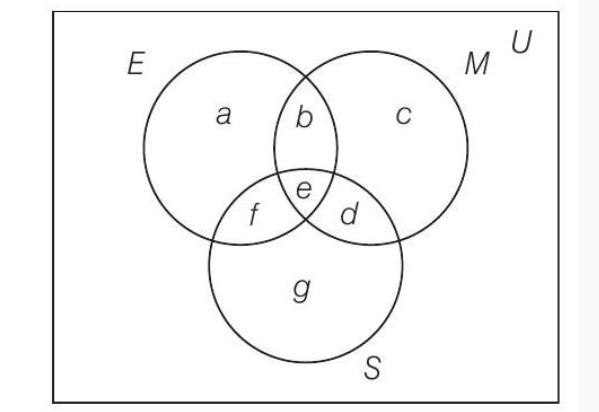
and
| Also, |
|
|---|---|
| om Eqs. (vi) and (vii), | |
| rom Eqs. (v) and (vii), | |
| rom Eqs. (iv) and (vii), |
On substituting the values of
On substituting the value of
On substituting
(i) Number of students who passed in English and Mathematics but not in Science
(ii) Number of students who passed in Mathematics and Science but not in English
(iii) Number of students who passed in Mathematics only
(iv) Number of students who passed in more than one subject
Alternate Method
Let
Now,
(i) Number of students passed in English and Mathematics but not in Science
(ii) Number of students passed in Mathematics and Science but not in English.
(iii) Number of students passed in mathematics only
(iv) Number of students passed in more than one subject only
25. In a class of 60 students, 25 students play cricket and 20 students play tennis and 10 students play both the games. Find the number of students who play neither.
Show Answer
Solution
Let
26. In a survey of 200 students of a school, it was found that 120 study Mathematics, 90 study Physics and 70 study Chemistry, 40 study Mathematics and Physics, 30 study Physics and Chemistry, 50 study Chemistry and Mathematics and 20 none of these subjects. Find the number of students who study all the three subjects.
Show Answer
Thinking Process
To solve this problem, use the formula for all the three subjects
Solution
Let
Then,
So, the number of students who study all the three subjects is 20 .
27. In a town of 10000 families, it was found that
(i) the number of families which buy newspaper
(ii) the number of families which buy none of
Show Answer
Solution
Let
Then,
(i) Number of families which buy newspaper
=(40-5-4+2)%=33 %
(ii) Number of families which buy none of
=100-[40+20+10-5-3-4+2] =100-60 %=40 %
28. In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows French
(i) only French.
(ii) only English.
(iii) only Sanskrit.
(iv) English and Sanskrit but not French.
(v) French and Sanskrit but not English.
(vi) French and English but not Sanskrit.
(vii) atleast one of the three languages.
(viii) none of the three languages.
Show Answer
Solution
Let
Then,
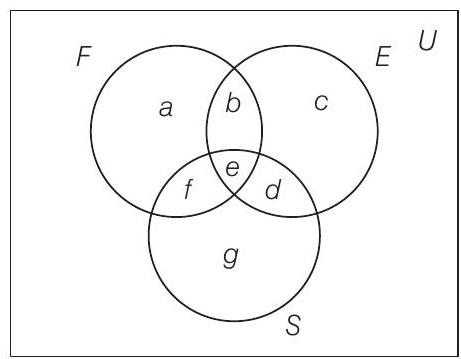
From Eqs. (vi) and (vii),
From Eqs. (v)and (vii),
From Eqs. (iv) and (vii),
On substituting the values of
On substituting the values of
(ii), we get
On substituting the values of
(i), we get
(i) Number of students who study French only,
(ii) Number of students who study English only,
(iii) Number of students who study Sanskrit only,
(iv) Number of students who study English and Sanskrit but not French,
(v) Number of students who study French and Sanskrit but not English,
(vi) Number of students who study French and English but not Sanskrit,
(vii) Number of students who study atleast one of the three languages
(viii) Number of students who study none of three languages
Objective Type Questions
29. Suppose,
(a) 15
(b) 3
(c) 45
(d) 35
Show Answer
Thinking Process
First find the total number of elements for the both sets, then compare them.
Solution
(c) If elements are not repeated, then number of elements in
But each element is used 10 times, so
If elements in
-
Option (a) 15: This option is incorrect because if ( n = 15 ), then the total number of elements in ( B_1, B_2, \ldots, B_{15} ) would be ( 3 \times 15 = 45 ). Since each element is repeated 9 times, the total number of unique elements would be ( \frac{45}{9} = 5 ), which contradicts the given condition that ( S ) has 15 unique elements.
-
Option (b) 3: This option is incorrect because if ( n = 3 ), then the total number of elements in ( B_1, B_2, \ldots, B_3 ) would be ( 3 \times 3 = 9 ). Since each element is repeated 9 times, the total number of unique elements would be ( \frac{9}{9} = 1 ), which contradicts the given condition that ( S ) has 15 unique elements.
-
Option (d) 35: This option is incorrect because if ( n = 35 ), then the total number of elements in ( B_1, B_2, \ldots, B_{35} ) would be ( 3 \times 35 = 105 ). Since each element is repeated 9 times, the total number of unique elements would be ( \frac{105}{9} \approx 11.67 ), which is not an integer and contradicts the given condition that ( S ) has 15 unique elements.
30. Two finite sets have
(a) 4,7
(b) 7,4
(c) 4,4
(d) 7,7
Show Answer
Thinking Process
We know that, if a set A contains n elements, then the number of subsets of
Solution
(a) Since, number of subsets of a set containing melements is 112 more than the subsets of the set containing
-
Option (b) 7,4: This option is incorrect because if ( m = 7 ) and ( n = 4 ), then the number of subsets of the first set would be ( 2^7 = 128 ) and the number of subsets of the second set would be ( 2^4 = 16 ). The difference between the number of subsets would be ( 128 - 16 = 112 ), which matches the given condition. Therefore, this option is actually correct, not incorrect.
-
Option (c) 4,4: This option is incorrect because if ( m = 4 ) and ( n = 4 ), then the number of subsets of both sets would be ( 2^4 = 16 ). The difference between the number of subsets would be ( 16 - 16 = 0 ), which does not match the given condition of 112 more subsets.
-
Option (d) 7,7: This option is incorrect because if ( m = 7 ) and ( n = 7 ), then the number of subsets of both sets would be ( 2^7 = 128 ). The difference between the number of subsets would be ( 128 - 128 = 0 ), which does not match the given condition of 112 more subsets.
31. The set
(a)
(b)
(c)
(d)
Show Answer
Solution
(b) We know that,
-
Option (a):
-
Option (c):
-
Option (d):
32. Let
(a)
(b)
(c)
(d)
Show Answer
Solution
(d) Every rectangle, rhombus, square in a plane is a parallelogram but every trapezium is not a parallelogram.
So,
-
(a)
-
(b)
-
(c)
33. Let
(a)
(b)
(c)
(d)
Show Answer
Solution
(c) The given sets can be represented in Venn diagram as shown below
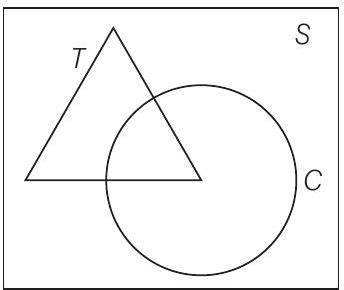
It is clear from the diagram that,
-
(a)
-
(b)
-
(d)
34. If
(a)
(b)
(c)
(d)
Show Answer
Solution
(d) Since,
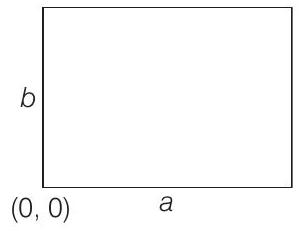
-
Option (a) is incorrect because it includes the boundary points of the rectangle, i.e., it includes points where ( x = 0 ), ( x = a ), ( y = 0 ), and ( y = b ). The problem specifies points inside the rectangle, which excludes the boundary.
-
Option (b) is incorrect because it includes the boundary points where ( y = 0 ) and ( y = b ). The problem specifies points inside the rectangle, which excludes the boundary.
-
Option (c) is incorrect because it includes the boundary points where ( x = 0 ) and ( x = a ). The problem specifies points inside the rectangle, which excludes the boundary.
35. In a town of 840 persons, 450 persons read Hindi, 300 read English and 200 read both. Then, the number of persons who read neither, is
(a) 210
(b) 290
(c) 180
(d) 260
Show Answer
Solution
(b) Let
Then,
Number of persons who read neither
-
Option (a) 210: This option is incorrect because the calculation for the number of persons who read neither Hindi nor English is based on the principle of inclusion-exclusion. The correct calculation shows that 290 persons read neither, not 210. The error in this option likely arises from a miscalculation or misunderstanding of the principle.
-
Option (c) 180: This option is incorrect for the same reason as option (a). The principle of inclusion-exclusion correctly calculates the number of persons who read neither Hindi nor English as 290. The number 180 does not fit the correct calculation and is therefore incorrect.
-
Option (d) 260: This option is also incorrect because, according to the principle of inclusion-exclusion, the number of persons who read neither Hindi nor English is 290. The number 260 is a result of an incorrect calculation or misunderstanding of the principle.
36. If
(a)
(b)
(c)
(d)
Show Answer
Thinking Process
If every element of
Solution
(a)
Clearly, every elements of
-
(b)
-
(c)
-
(d)
37. A survey shows that
(a)
(b)
(c)
(d)
Show Answer
Solution
(c) Let
-
Option (a)
-
Option (b)
-
Option (d)
38. If sets
(a)
(b)
(c)
(d)
Show Answer
Solution
(c) Let
-
(a)
-
(b)
-
(d)
39. If
(a)
(b)
(c)
(d)
Show Answer
Solution
(a)
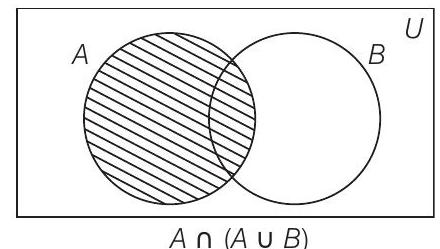
-
Option (b)
-
Option (c)
-
Option (d)
40. If
(a)
(b)
(c) A
(d) B
Show Answer
Thinking Process
To solve this problem, use the distributive law i.e.,
Solution
(b)
-
Option (a)
-
Option (c) A: This option is incorrect because the expression
-
Option (d) B: This option is incorrect because the expression
41. If
(a) 34
(b) 31
(c) 33
(d) 41
Show Answer
Solution
(d)
and
-
Option (a) 34: This option is incorrect because it assumes that the total number of elements in sets ( S ) and ( P ) is 34. However, the correct total is 41, as ( n(S) = 33 ) and ( n(P) = 8 ), making ( n(S) + n(P) = 41 ).
-
Option (b) 31: This option is incorrect because it assumes that the total number of elements in sets ( S ) and ( P ) is 31. However, the correct total is 41, as ( n(S) = 33 ) and ( n(P) = 8 ), making ( n(S) + n(P) = 41 ).
-
Option (c) 33: This option is incorrect because it assumes that the total number of elements in sets ( S ) and ( P ) is 33. However, the correct total is 41, as ( n(S) = 33 ) and ( n(P) = 8 ), making ( n(S) + n(P) = 41 ).
42. If
(a)
(b)
(c)
(d)
Show Answer
Solution
(c)
-
Option (a)
-
Option (b)
-
Option (d)
Fillers
43. The set
Show Answer
Solution
The set
44. When
Show Answer
Solution
So, number of element in
45. If
Show Answer
Solution
If
46. If
Show Answer
Solution
If

47. Power set of the set
Show Answer
Thinking Process
We know that, the power set is a collection of all the subset of a set. To solve this problem, write the all subset of the given set.
Solution
So, the subsets of
48. If the sets
Show Answer
Solution
Universal set for
49. If
(i)
(ii)
Show Answer
Solution
If
(i)
(ii)
50. For all sets
Show Answer
Solution
51. Match the following sets for all sets
| Column I | Column II | ||
|---|---|---|---|
| (i) | (a) | ||
| (ii) | (b) | ||
| (iii) | (c) | ||
| (iv) | (d) | ||
| (v) | (e) | ||
| (vi) | (f) |
Show Answer
Solution
(i)
(ii)
(iii)
Alternate Method
It is clear from the diagram,
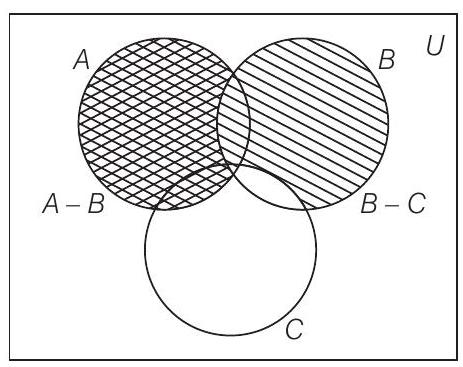
(iv)
(v)
(vi)
Hence, the correct matches are
(i)
(ii)
(iii)
(iv)
(v)
(vi)
True/False
52. If
Show Answer
Solution
True
Since, every set is the subset of itself.
Therefore, for any set
53. If
Show Answer
Solution
False
Since, every elements of
54. The sets
Show Answer
Solution
False
| Since, | |
|---|---|
| But | |
55.
Show Answer
Solution
True
Since, every integer is also a rational number, then
where,
56. Let sets
Show Answer
Solution
True
Thus, this every elements of
57. Given
Show Answer
Solution
False
So,










