Chapter 05 States of Matter
Multiple Choice Questions (MCQs)
1. A person living in Shimla observed that cooking food without using pressure cooker takes more time. The reason for this observation is that at high altitude
(a) pressure increases
(b) temperature decreases
(c) pressure decreases
(d) temperature increases
Show Answer
Answer
(c) Pressure at the top of a mountain [or at high altitude] is low. This suggests that boiling takes place at lower temperature, due to which things take more time to boil.
However, in a pressure cooker, pressure is increased and hence, boiling point increases. Thus, things comes to boil in a pressure cooker in a less period of time.
-
(a) Pressure increases: This is incorrect because at high altitudes, atmospheric pressure actually decreases, not increases. Increased pressure would lead to a higher boiling point, which is not the case at high altitudes.
-
(b) Temperature decreases: While it is true that temperatures can be lower at high altitudes, this is not the primary reason why cooking takes longer. The main factor is the decreased atmospheric pressure, which lowers the boiling point of water.
-
(d) Temperature increases: This is incorrect because temperatures generally decrease with altitude. Even if temperatures were to increase, it would not explain the longer cooking times, which are primarily due to the lower boiling point caused by decreased pressure.
2. Which of the following property of water can be used to explain the spherical shape of rain droplets?
(a) Viscosity
(b) Surface tension
(c) Critical phenomena
(d) Pressure
Show Answer
Answer
(b) The spherical shape of rain droplets is due to surface tension. The lowest energy state of a liquid will be when the surface area is minimum. Surface tension tries to decrease the surface area of the liquid to the minimum. The rain droplets are spherical because for a given volume, a sphere has minimum surface area.
-
Viscosity: Viscosity is a measure of a fluid’s resistance to flow. It does not directly influence the shape of droplets but rather affects how quickly they can move or spread. Therefore, it is not responsible for the spherical shape of rain droplets.
-
Critical phenomena: Critical phenomena refer to the behavior of physical systems during phase transitions, such as the transition from liquid to gas. This concept does not explain the shape of droplets but rather the conditions under which different phases coexist. Hence, it is not related to the spherical shape of rain droplets.
-
Pressure: Pressure is the force exerted per unit area. While pressure can influence the formation and behavior of droplets, it does not determine their shape. The spherical shape is specifically due to surface tension minimizing the surface area, not pressure.
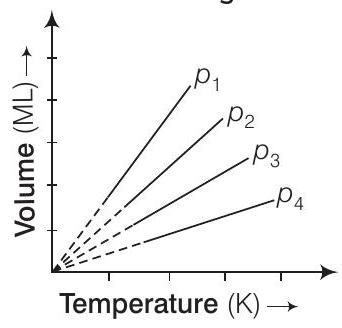
3. A plot of volume
(a)
(b)
(c)
(d)
Show Answer
Thinking Process
The question is based upon Boyle’s law. It states that at constant temperature, the volume of a given proportional to its pressure. i.e.,
Answer
(c) At a particular temperature,
-
Option (a)
-
Option (b)
-
Option (d)
4. The interaction energy of London force is inversely proportional to sixth power of the distance between two interacting particles but their magnitude depends upon
(a) charge of interacting particles
(b) mass of interacting particles
(c) polarisability of interacting particles
(d) strength of permanent dipoles in the particles
Show Answer
Answer
(c) London dispersion forces operate only over very short distance. The energy of interaction varies as
Large or more complex are the molecules, greater is the magnitude of London forces. This is obviously due to the fact that the large electron clouds are easily distorted or polarised.
Hence, greater the polarisability of the interacting particles, greater is the magnitude of the interaction energy.
-
(a) Charge of interacting particles: London dispersion forces are a type of van der Waals force that arise due to temporary dipoles induced in atoms or molecules. These forces do not depend on the charge of the interacting particles, as they occur even between neutral atoms and molecules.
-
(b) Mass of interacting particles: While the mass of the particles can influence the overall strength of the London dispersion forces indirectly (since larger mass often correlates with larger size and more electrons), the interaction energy itself is not directly dependent on the mass. It is more directly related to the polarisability of the electron cloud.
-
(d) Strength of permanent dipoles in the particles: London dispersion forces are specifically due to temporary dipoles and not permanent dipoles. The strength of permanent dipoles is relevant to other types of intermolecular forces, such as dipole-dipole interactions, but not to London dispersion forces.
5. Dipole-dipole forces act between the molecules possessing permanent dipole. Ends of dipoles possess ‘partial charges’. The partial charge is
(a) more than unit electronic charge
(b) equal to unit electronic charge
(c) less than unit electronic charge
(d) double the unit electronic charge
Show Answer
Answer
(c) Dipole-dipole forces act between the molecules possessing permanent dipole and ends of dipoles possess ‘partial charges’. Partial charges present on ends of a dipole are always less than the unit electronic charge.
e.g.,
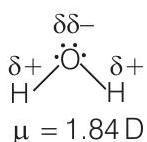
-
(a) more than unit electronic charge: This option is incorrect because partial charges on the ends of a dipole are always less than the unit electronic charge. A unit electronic charge refers to the charge of a single electron or proton, which is a fundamental constant. Partial charges arise due to the unequal sharing of electrons between atoms in a molecule and are always a fraction of the unit electronic charge.
-
(b) equal to unit electronic charge: This option is incorrect because partial charges are not equal to the unit electronic charge. The unit electronic charge is a fixed value (approximately 1.602 x 10^-19 coulombs), while partial charges are smaller and result from the distribution of electron density in a molecule. They represent a fraction of the unit electronic charge.
-
(d) double the unit electronic charge: This option is incorrect because partial charges cannot exceed the unit electronic charge, let alone be double it. Partial charges are always less than the unit electronic charge, as they represent the slight imbalance in electron distribution between atoms in a molecule, not a full transfer of electrons.
6. The pressure of a 1:4 mixture of dihydrogen and dioxygen enclosed in a vessel is one atmosphere. What would be the partial pressure of dioxygen?
(a)
(b)
(c)
(d)
Show Answer
Answer
(c) Given that, pressure of a
-
Option (a)
-
Option (b)
-
Option (d)
7. As the temperature increases, average kinetic energy of molecules increases. What would be the effect of increase of temperature on pressure provided the volume is constant?
(a) Increases
(b) Decreases
(c) Remains same
(d) Becomes half
Show Answer
Thinking Process
This problem is based on Gay-Lussac’s law which states that “volume remaining constant, the pressure of a given mass of a gas is directly proportional to its temperature in degrees Kelvin”.
Answer
(a) As the temperature increases, average kinetic energy of molecules increases. From Gay-Lussac’s law, at constant volume, as the temperature is increased, pressure increases.
-
(b) Decreases: This option is incorrect because, according to Gay-Lussac’s law, at constant volume, an increase in temperature results in an increase in pressure, not a decrease.
-
(c) Remains same: This option is incorrect because, according to Gay-Lussac’s law, at constant volume, an increase in temperature leads to an increase in pressure, so the pressure cannot remain the same.
-
(d) Becomes half: This option is incorrect because, according to Gay-Lussac’s law, at constant volume, an increase in temperature causes an increase in pressure, not a decrease to half.
8. Gases possess characteristic critical temperature which depends upon the magnitude of intermolecular forces between the particles. Following are the critical temperatures of some gases.
| Gases | ||||
|---|---|---|---|---|
| Critical temperature in Kelvin | 33.2 | 5.3 | 154.3 | 126 |
From the above data what would be the order of liquefaction of these gases? Start writing the order from the gas liquefying first
(a)
(b)
(c)
(d)
Show Answer
Answer
(d) Higher the critical temperature, more easily is the gas liquified. Hence, order of liquefaction starting with the gas liquefying first will be
Note Critical temperature of a gas may be defined as that temperature above which it cannot be liquified howsoever high pressure may be applied on the gas.
-
Option (a)
- Incorrect because
- Incorrect because
-
Option (b)
- Incorrect because
- Incorrect because
-
Option (c)
- Incorrect because
- Incorrect because
9. What is SI unit of viscosity coefficient
(a) Pascal
(b)
(c)
(d)
Show Answer
Answer
(b) The SI unit of viscosity coefficient
Substitute SI units of
Hence, the si unit of
-
(a) Pascal: Pascal (Pa) is the SI unit of pressure, not viscosity. Viscosity is a measure of a fluid’s resistance to flow, whereas pressure is the force exerted per unit area.
-
(c)
-
(d)
10. Atmospheric pressures recorded in different cities are as follows
| Cities | Shimla | Bangalore | Delhi | Mumbai |
|---|---|---|---|---|
Consider the above data and mark the place at which liquid will boil first.
(a) Shimla
(b) Bangalore
(c) Delhi
(d) Mumbai
Show Answer
Thinking Process
(i) A liquid boils when vapour pressure above it becomes equal to the atmospheric pressure. Lower the atmospheric pressure, lower is the boiling point.
(ii) Arrange the four cities according to the increase of atmospheric pressures and pick out the lowest one.
Answer
(a) Shimla has the lowest atmospheric pressure among all the four cities. Thus, at Shimla liquid will boil first because lower the atmospheric pressure, lower is the boiling point.
-
Bangalore: Bangalore has a higher atmospheric pressure (
-
Delhi: Delhi has a slightly higher atmospheric pressure (
-
Mumbai: Mumbai has the highest atmospheric pressure (
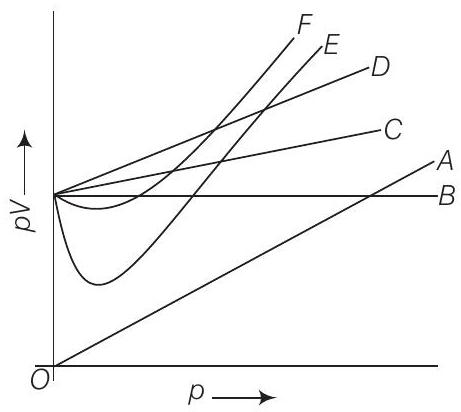
11. Which curve in figure represents the curve of ideal gas?
(a) Only B
(b)
(c)
(d)
Show Answer
Thinking Process
(i) The graph given in the question depend upon the Boyle’s law.
(ii) At constant temperature, the graph between
(iii) At constant temperature
Answer
(a) For ideal gas
-
Option (b)
-
Option (c)
-
Option (d)
12. Increase in kinetic energy can overcome intermolecular forces of attraction. How will the viscosity of liquid be affected by the increase in temperature?
(a) Increase
(b) No effect
(c) Decrease
(d) No regular pattern will be followed
Show Answer
Answer
(c) With increase of temperature, the kinetic energy of the molecules of liquid increases which can overcome the intermolecular forces. Hence, the liquid starts flowing.
In other words the viscosity of a liquid decreases with increase in temperature. It has been found that the decrease is about
-
(a) Increase: This option is incorrect because an increase in temperature leads to an increase in the kinetic energy of the molecules, which reduces the intermolecular forces of attraction, causing the liquid to flow more easily and thus decreasing its viscosity, not increasing it.
-
(b) No effect: This option is incorrect because temperature has a significant effect on the kinetic energy of molecules. As temperature increases, the kinetic energy increases, which reduces the intermolecular forces and decreases the viscosity of the liquid.
-
(d) No regular pattern will be followed: This option is incorrect because there is a well-established relationship between temperature and viscosity. As temperature increases, the viscosity of a liquid consistently decreases, following a regular pattern.
13. How does the surface tension of a liquid vary with increase in temperature?
(a) Remains same
(b) Decreases
(c) Increases
(d) No regular pattern is followed
Show Answer
Answer
(b) The surface tension of liquids generally decreases with increase of temperature and becomes zero at the critical temperature. The decrease in surface tension with increase of temperature is obviously due to the fact that with increase of temperature, the kinetic energy of the molecules increases and therefore, the intermolecular attraction decreases.
Note Surface tension of a liquid is defined as the force acting at right angles to the surface along one centimetre length of the surface. Units of surface tension are dyne per
-
(a) Remains same: This option is incorrect because surface tension is influenced by temperature. As temperature increases, the kinetic energy of the molecules also increases, leading to a decrease in intermolecular forces and thus a decrease in surface tension. Therefore, surface tension does not remain the same with an increase in temperature.
-
(c) Increases: This option is incorrect because an increase in temperature results in higher kinetic energy of the molecules, which reduces the intermolecular forces. Consequently, the surface tension decreases rather than increases with an increase in temperature.
-
(d) No regular pattern is followed: This option is incorrect because there is a well-established pattern that surface tension decreases with an increase in temperature. The relationship between temperature and surface tension is predictable and consistent, contrary to the suggestion that no regular pattern is followed.
Multiple Choice Questions (More Than One Options)
14. With regard to the gaseous state of matter which of the following statements are correct?
(a) Complete order of molecules
(b) Complete disorder of molecules
(c) Random motion of molecules
(d) Fixed position of molecules
Show Answer
Answer
In gaseous state, molecules are in a state of random motion i.e., it is the state in which molecules are disorderly arranged. Gaseous state have higher entropy than the liquid as well as solid.
-
(a) Complete order of molecules: This is incorrect because in the gaseous state, molecules are not in a state of complete order. Instead, they are in a state of complete disorder and move randomly.
-
(d) Fixed position of molecules: This is incorrect because in the gaseous state, molecules do not have fixed positions. They move freely and randomly throughout the available space.
15. Which of the following figures does not represent 1 mole of dioxygen gas at STP?
(a)
(b)
(c)
(d)
Show Answer
Answer
It is known that, 1 mole of a gas = gram molecular mass = Avogadro’s number of molecules
Thus, 1 mole of
-
(a)
-
(b)
-
(d)
16. Under which of the following conditions applied together, a gas deviates most from the ideal behaviour?
(a) Low pressure
(c) Low temperature
(b) High pressure
(d) High temperature
Show Answer
Answer
(
A gas which obeys the ideal gas equation,
However, there is no gas which obeys the ideal gas equation under all conditions of temperature and pressure. Hence, the concept of ideal gas is only theoretical or hypothetical. The gases are found to obey the gas laws fairly well when the pressure is low or the temperature is high.
Such gases are, therefore, known as ‘real gases’. All gases are real gases. Hence, at high pressure and low temneratıre a real gas deviates most from ideal hehaviour.
- At low pressure, gas molecules are far apart, and intermolecular forces are negligible, so the gas behaves more ideally.
- At high temperature, the kinetic energy of gas molecules is high, which overcomes intermolecular forces, leading to more ideal behavior.
17. Which of the following changes decrease the vapour pressure of water kept in a sealed vessel ?
(a) Decreasing the quantity of water
(b) Adding salt to water
(c) Decreasing the volume of the vessel to one-half
(d) Decreasing the temperature of water
Show Answer
Answer
When salt is added, less surface area is available for the water molecules to vaporise because salt molecules occupy the position of water molecules on the surface. Hence, vapour pressure of the water decreases.
Moreover, vapour pressure also decreases with decrease in temperature because kinetic energy of the molecules decrease.
-
Decreasing the quantity of water: The vapour pressure of a liquid in a sealed container depends on the temperature and the nature of the liquid, not on the quantity of the liquid. Therefore, decreasing the quantity of water does not affect the vapour pressure.
-
Decreasing the volume of the vessel to one-half: The vapour pressure of a liquid in a sealed container is independent of the volume of the container. It is determined by the temperature and the nature of the liquid. Hence, decreasing the volume of the vessel does not change the vapour pressure.
Short Answer Type Questions
18. If
Show Answer
Answer
From Avogadro’s law, we know that
Volume of 1 mole of the gas
Volume occupied by
Similarly, volume occupied by
Volume occupied by
Volume occupied by
Thus,
Show Answer
Answer
Physical properties of ice, water and steam are very different because they found in different states. Ice found in solid, water found in liquid and steam found in vapour states. The chemical composition of water in all the three states (ice, water and steam) is same, i.e.,
Show Answer
Answer
Temperature, pressure, mass and volume are the factors which determine the different states of matter. i.e., solid, liquid and gas.
Stronger intermolecular forces result in higher boiling point.
Strength of London forces increases with the number of electrons in the molecule.
Boiling point of
(a) Which type of intermolecular forces are present in the molecules HF,
(b) Looking at the trend of boiling points of
(c) Why is boiling point of hydrogen fluoride highest while that of hydrogen chloride lowest?
Show Answer
Answer
From the information and data given in the question, we concluded that
(a) In
(b) Electronegativity of chlorine, bromine and iodine decreases in the order are present
Therefore, dipole moment should decrease from
This is so because London forces increases as the number of electrons in a molecule increases and in this case number of electrons is increasing from
(c) Hydrogen fluoride has highest dipole moment attributes due to highest electronegativity of fluorine as well as presence of hydrogen bonding in HF. Therefore, HF has highest boiling point.
Show Answer
Answer
When temperature and pressure of a gas is
Show Answer
Answer
At low pressure and high temperature, a real gas behaves as an ideal gas. Almost all gases are real gas.
Show Answer
Answer
The temperature above which a gas cannot be liquefied howsoever high pressure may be applied on the gas is called critical temperature. Since, gas ‘A’ liquifies easily, this suggests gas ’
On the other hand, gas ’
Show Answer
Answer
Unit of
Show Answer
Answer
This statement is correct only for ideal gases. It is not possible to liquefy an ideal gas because there is no intermolecular forces of attractions between the molecules of an ideal gas.
Water, alcohol
Show Answer
Answer
In the above given molecules, only hexane
However,
hexane
Greater is the attractive forces between the molecules, greater is the magnitude of surface tension of liquid.
Show Answer
Answer
Whenever a gas is collected over water, it is moist and saturated with water vapours which exert their own pressure. The pressure due to water vapours is called aqueous tension thus, the total pressure of the gas (
Thus,
Show Answer
Answer
The energy which arises due to motion of atoms or molecules in a body is known as thermal energy. It is a measure of average kinetic energy of the particles. It increases with increase in temperature.
Show Answer
Answer
State and explain the evidence that shows that the assumption is not applicable for real gases.
Show Answer
Answer
Real gases can be liquefied by cooling and compressing the gas. This proves that force of attraction exist among the molecules.
(i) What is the value of
(ii) For real gas what will be the effect on value of
Show Answer
Answer
(i) For ideal gas, compressibility factor,
(ii) Above Boyle’s temperature, real gases show positive deviation. So,
Note Following important points come out from the compressibility factor,
(i) For ideal gas
(ii) At very low pressure all gases shown have
(iii) At high pressure, all the gases have
(iv) At intermediate pressures most gases have
Show Answer
Answer
The given critical temperature and pressure of
where, ’
(i) Arrange the following gases in the increasing order of ’
(ii) Arrange the following gases in the decreasing order of magnitude of ’
Show Answer
Answer
(i) Molar volume occupied by the gas molecules
(ii) van der Waals’ constant ’
Greater the size of electron cloud, greater is the polarisability of the molecule and greater is the dispersion forces or London forces.
(i) If pressure is taken in
(ii) What will be the unit of ’
Show Answer
Answer
Given that,
(i)
units of
then, units of
(ii) If units of
then, units of
Show Answer
Answer
Two phenomena that can be explained on the basis of surface tension are as following
(i) Rise or fall of the liquid in a capillary-(capillary action).
(ii) Spherical shape of small liquid drops.
Show Answer
Thinking Process
Stronger the intermolecular forces existing between the liquids, more viscous is the liquid.
Answer
In water and glycerine - Hydrogen bonding and dipole-dipole interactions exists as both are polar molecules.
hexane - Dispersion forces/London forces are present due ts non-polar nature. The order of intermolecular forces among the given liquids is, hexane
Since, hexane has weakest intermolecular forces and glycerine the strongest (three
Show Answer
Answer
As the temperature of a liquid increases, kinetic energy of the molecules increases which can overcome intermolecular forces. So, the liquid can flow more easily, this results in decrease in viscosity of the liquid.
(i) How will the volume of a gas change if its pressure is increased at constant temperature?
(ii) At a constant pressure, how will the volume
of a gas change if the temperature is increased from
Show Answer
Answer
(i) In accordance to Boyle’s law, pressure of a gas is inversly proportional to its volume if temperature is kept constant. Thus, the volume of a gas will decrease if the pressure on the gas is increased keeping the temperature constant. e.g., at
(ii) In accordance to Iharles law, volume of a gas is directly proportional to its temperature if pressure is kept constant.
Thus, on increasing temperature, the volume of a gas will increase if pressure is kept constant.
At constant

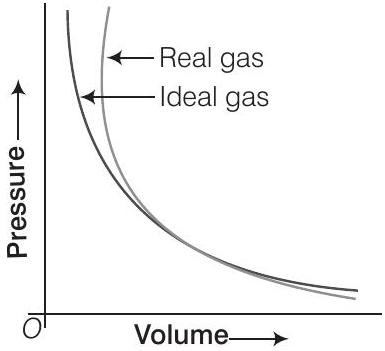
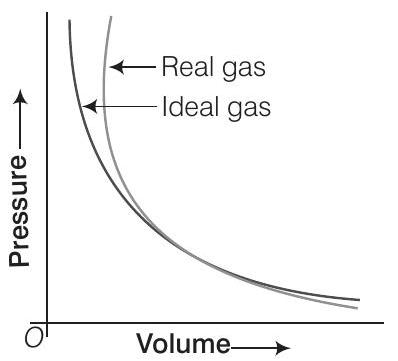
(i) Interpret the behaviour of real gas with respect to ideal gas at low pressure.
(ii) Interpret the behaviour of real gas with respect to ideal gas at high pressure.
(iii) Mark the pressure and volume by drawing a line at the point where real gas hehaves as an ideal qas
Show Answer
Answer
(i) At low pressure, the real gas shows very small deviation from ideal behaviour because the two curves almost coincide at low pressure.
(ii) At high pressure, the real gas show large deviations from ideal behaviour as the curves are far apart.
(iii) At point ’
Matching The Columns
41. Match the graphs between the following variables with their names.
| Graphs | Names | |
|---|---|---|
| A.Pressure vs temperature graph at constant molar volume |
1. | Isotherms |
| B.Pressure vs volume graph at constant temperature |
2. | Constant temperature curve |
| C.Volume vs temperature graph at constant pressure |
3. | Isochores |
Show Answer
Answer
A.
B.
C.
A. When molar volume is constant, the
B. When temperature is constant, the
C. When pressure is constant,
| A. | Boyle’s law | 1. | |
|---|---|---|---|
| B. | Charle’s law | 2. | |
| C. | Dalton’s law | 3. | |
| D. | Avogadro’s law | 4. | |
| 5. |
Show Answer
Answer
A.
B.
C.
D.
A. Boyle’s law,
B. Charle’s law,
C. Dalton’s law,
D. Avogadro’s law,
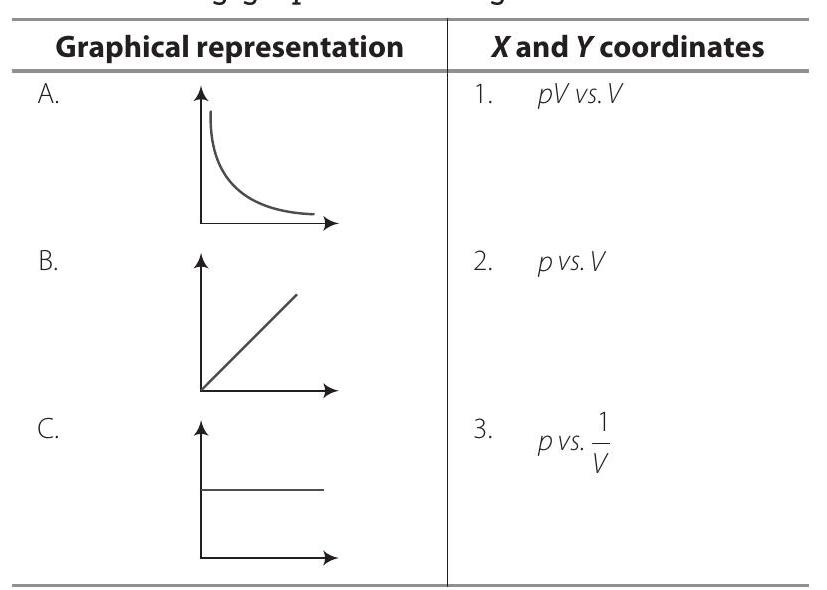
Show Answer
Answer
A.
B.
C.

In the following questions a statement of Assertion (A) followed by a statement of Reason (
Assertion (A) Three states of matter are the result of balance between intermolecular forces and thermal energy of the molecules.
Reason (R) Intermolecular forces tend to keep the molecules together but thermal energy of molecules tends to keep them apart.
(a) Both
(b) Both
(c)
(d)
Show Answer
Answer
(a) Both assertion and reason are true and reason is the correct explanation of assertion. Intermolecular forces and thermal energy decide the state of matter because the former kept the molecules together but later keep them apart.
Reason (R) At high pressure all gases have
(a) Both
(b) Both
(c)
(d)
Show Answer
Answer
(b) Both assertion and reason are true but reason is not the correct explanation of assertion. At constant temperature,
Reason (R) At high altitude atmospheric pressure is high.
(a) Both
(b) Both
(c)
(d)
Show Answer
Answer
(c) Assertion is true but reason is false.
At high altitude, atmospheric pressure is low.
Reason (R) Above critical temperature, the molecular speed is high and intermolecular attractions cannot hold the molecules together because they escape because of high speed.
(a) Both
(b) Both
(c)
(d)
Show Answer
Answer
(a) Both assertion and reason are true and reason is the correct explanation of assertion. Gases do not liquefy above their critical temperature, even an applying high pressure because above critical temperature, the molecular speed is high and intermolecular attractions cannot hold the molecules together.
Reason (R) The density of liquid and gaseous phase is equal to critical temperature.
(a) Both
(b) Both
(c)
(d)
Show Answer
Answer
(a) Both assertion and reason are true and reason is the correct explanation of assertion. At critical temperature, density of liquid and gaseous phase becomes equal. Due to which liquid passes into gaseous state imperceptibly and continuously.
Reason (R) Small liquid drops have spherical shape.
(a) Both
(b) Both
(c)
(d)
Show Answer
Answer
(d) Assertion is false but reason is true.
Liquid tend to reduce number of molecules or surface tension at there surface, that’s why small liquid drops have spherical shape.
Long Answer Type Questions
50. Isotherms of carbon dioxide at various temperatures are represented in figure. Answer the following questions based on this figure.
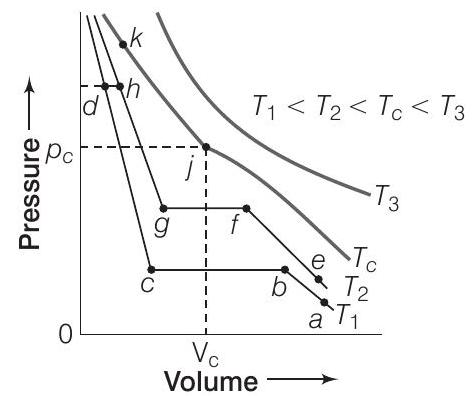
(i) In which state will
(ii) At what point will
(iii) At what point will
(iv) Will condensation take place when the temperature is
(v) What portion of the isotherm at
Show Answer
Answer
(i) In gaseous state,
(ii) At point
(iii) Similarly, at temperature
(iv) Condensation will not take place at
(v) Between
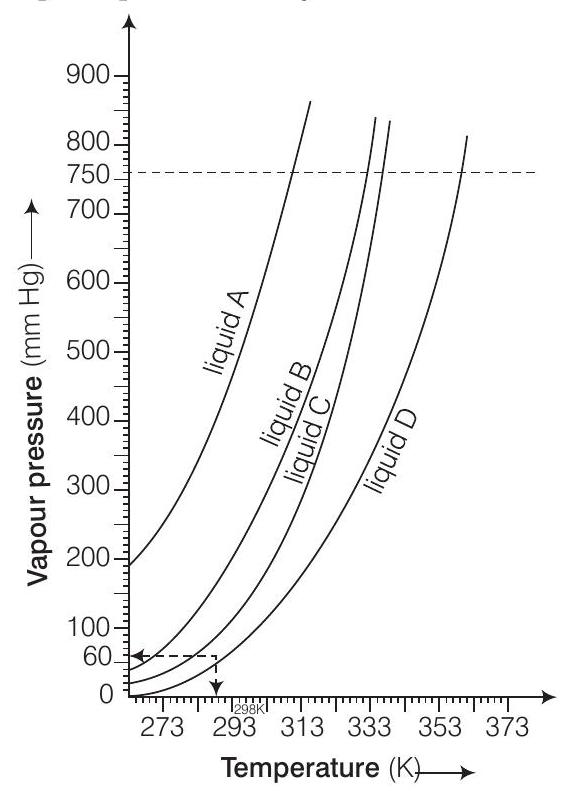
(i) Calculate graphically boiling points of liquids
(ii) If we take liquid
(iii) At high altitude, atmospheric pressure is low (say
(iv) Pressure cooker is used for cooking food at hill station. Explain in terms of vapour pressure why is it so?
Show Answer
Answer
(i) Boiling point of
(ii) In a closed vessel, liquid
(iii) Temperature corresponding to
(iv) A liquid boils when vapour pressure becomes equal to the atmospheric pressure. However at high altitudes i.e., on, hills, water boils at low temp erature due to low atmospheric pressure. But when pressure cooker is used, the vapour pressure of water is increased due to which water boils at even lower temperature within a short period of time
Show Answer
Answer
In a closed vessel, it is essential to know that below the critical point (i.e., critical temperature and critical pressure), the surface of separation between the liquid and its vapour is clearly visible. As we approach towards the critical point, the density of the liquid decreases while that of the vapour increases due to compression.

Below critical point
(Meniscus clearly visible)

Above critical point (Meniscus disappears)
At the critical point, the densities of the liquid and that of the vapour become equal and the surface of separation disappears i.e., the liquid and the gaseous state become not separable. In other words, the meniscus is no longer visible.
The fluid which is now a homogeneous mixture is called supercritical fluid. Hence, any fluid above its critical temperature and pressure is called a supercritical fluid.
These supercritical fluids dissolve many organic substances. They are used for quick separation of a mixture into its components. e.g.,
It is used to dissolve out caffeine from coffee beans as it is a better substitute than chlorofluorocarbons which are harmful for the environment.
Show Answer
Answer
Sharp glass edges are heated to make them smooth. Because on heating glass melts and the surface of the liquid tends to take the rounded shape at the edges which has minimum surface area. This is called fire polishing of glass.
Show Answer
Answer
When a liquid flows over a fixed surface, the layer of molecules in the immediate contact of surface is stationary. The velocity of the upper layers increases as the distance of layers from the fixed layer increases.
This type of flow in which there is a regular gradation of velocity in passing from one layer to the next is called laminar flow.
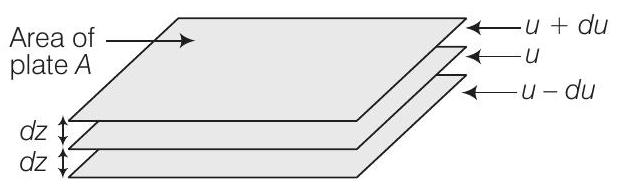
In laminar flow, the velocity of molecules is not same in all the layers because every layer offers some resistance or friction to the layer immediately below it.
55. Isotherms of carbon dioxide gas are shown in figure. Mark a path for changing gas into liquid such that only one phase (i.e., either a gas or a liquid) exists at any time during the change. Explain how the temperature, volume and pressure should be changed to carry out the change?
Show Answer
Answer
It is possible to change a gas into a liquid or a liquid into a gas by a process such that there is always a single phase present.
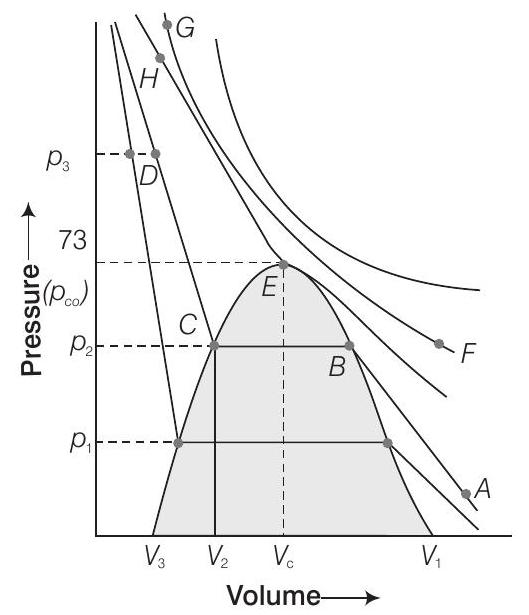
e.g., In figure given above, we can move from
Now, we can move vertically down towards
It process is carried out at the critical temperature, substance always remains in one phase. This is called continuity of state between the gaseous and the liquid state.










