Conic Sections
Short Answer Type Questions
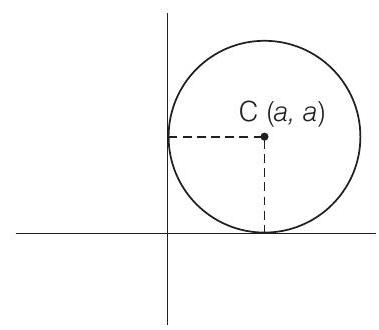
1. Find the equation of the circle which touches the both axes in first quadrant and whose radius is $a$.
Show Answer
Solution
Given that radius of the circle is a i.e., $(h, k)=(a, a)$
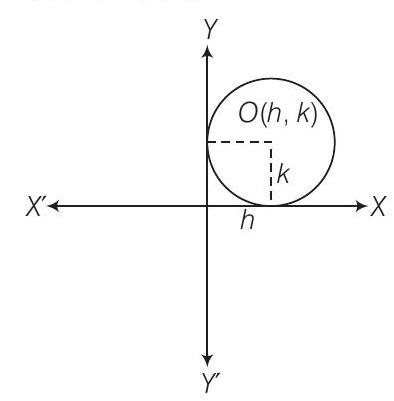
So, the equation of required circle is
$(x-a)^{2}+(y-a)^{2} =a^{2} \\ $
$\Rightarrow x^{2}-2 a x+a^{2}+y^{2}-2 a y+a^{2} =a^{2} \\ $
$\Rightarrow x^{2}+y^{2}-2 a x-2 a y+a^{2} =0 $
2. Show that the point $(x, y)$ given by $x=\frac{2 a t}{1+t^{2}}$ and $y=\frac{a(1-t^{2})}{1+t^{2}}$ lies on a circle.
Show Answer
Solution
Given points are
$ \begin{aligned} x & =\frac{2 a t}{1+t^{2}} \text { and } y=\frac{a(1-t^{2})}{1+t^{2}} \\ x^{2}+y^{2} & =\frac{4 a^{2} t^{2}}{(1+t^{2})^{2}}+\frac{a^{2}(1-t^{2})^{2}}{(1+t^{2})^{2}} \end{aligned} $
$ \Rightarrow \quad \frac{1}{a^{2}}(x^{2}+y^{2})=\frac{4 t^{2}+1+t^{4}-2 t^{2}}{(1+t^{2})^{2}} $
$ \begin{matrix} \Rightarrow & \frac{1}{a^{2}}(x^{2}+y^{2})=\frac{t^{4}+2 t^{2}+1}{(1+t^{2})^{2}} \\ \Rightarrow & \frac{1}{a^{2}}(x^{2}+y^{2})=\frac{(1+t^{2})^{2}}{(1+t^{2})^{2}} \\ \Rightarrow & x^{2}+y^{2}=a^{2}, \text { which is a required circle. } \end{matrix} $
3. If a circle passes through the points $(0,0),(a, 0)$ and $(0, b)$, then find the coordinates of its centre.
Show Answer
Thinking Process
General equation of the circle passing through the origin is $x^{2}+y^{2}+2 y x+2 f y=0$.
Now, satisfied the given points to get the values of $g$ and $f$. The centre of the circle is $(-g,-f)$.
Solution
Let the equation of circle is
$ x^{2}+y^{2}+2 g x+2 f y=0 $
Since, this circle passes through the points $A(0,0), B(a, 0)$ and $C(0, b)$.
$ \therefore \quad a^{2}+2 a g=0 $
$ \text { and } \quad b^{2}+2 b f=0 $
From Eq. (ii), $a+2 g=0 \Rightarrow g=-a / 2$
From Eq. (iii), $b+2 f=0 \Rightarrow f=-b / 2$
Hence, the coordinates of the circle are $\frac{a}{2}, \frac{b}{2}$.
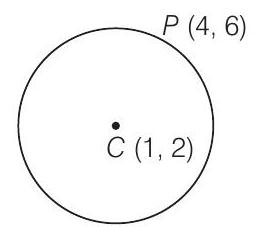
4. Find the equation of the circle which touches $X$-axis and whose centre is $(1,2)$.
Show Answer
Solution
Given that, centre of the circle is $(1,2)$.
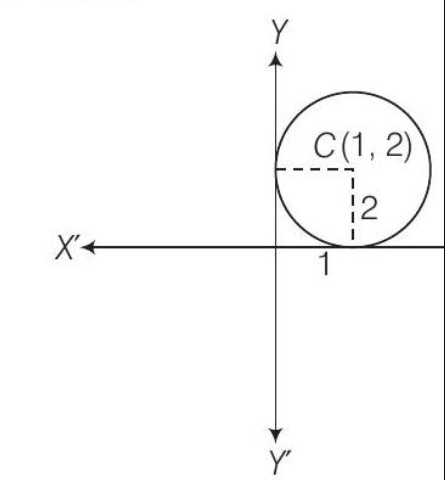
$\because \quad$ Radius $=2$
So, the equation of circle is
$\begin{aligned} & (x-1)^2+(y-2)^2 =2^2 \\ \Rightarrow & x^2-2 x+1+y^2-4 y+4 =4 \\ \Rightarrow & x^2-2 x+y^2-4 y+1 =0 \\ \Rightarrow & x^2+y^2-2 x-4 y+1 =0 \end{aligned}$
5. If the lines $3 x+4 y+4=0$ and $6 x-8 y-7=0$ are tangents to a circle, then find the radius of the circle.
Show Answer
Thinking Process
The distance between two parallel lines $a x+b y+c_1=0$ and $a x+b y+c_2=0$ is given by,
i.e., $d=|\frac{c_1-c_2}{\sqrt{a^{2}+b^{2}}}|$. Use this formula to solve the above problem.
Solution
Given lines,
or
$ \begin{matrix} 3 x-4 y+4=0 \\ 6 x-8 y-7=0 \\ 3 x-4 y-7 / 2=0 \end{matrix} $
It is clear that lines (i) and (ii) parallel.
Now, distance between them i.e.,
$ d=|\frac{4+7 / 2}{\sqrt{9+16}}|=|\frac{\frac{8+7}{2}}{5}|=3 / 2 $
$\therefore$ Distance between these line $=$ Diameter of these circle
$\therefore$ Diameter of the circle $=3 / 2$
and radius of the circle $=3 / 4$
6. Find the equation of a circle which touches both the axes and the line $3 x-4 y+8=0$ and lies in the third quadrant.
Show Answer
Solution
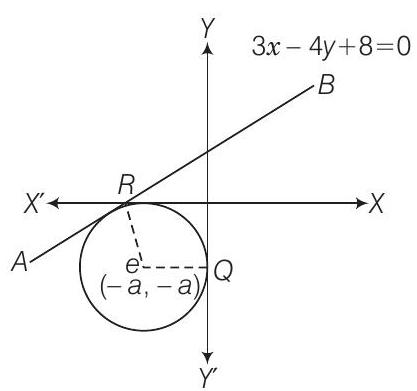
Let $a$ be the radius of the circle. Then, the coordinates of the circle are $(-a,-a)$. Now, perpendicular distance from $C$ to the line $A B=$ Radius of the circle
$ d=|\frac{-3 a+4 a+8}{\sqrt{9+16}}|=|\frac{a+8}{5}| \\ $
$\because a= \pm \frac{a+8}{5} \\ $
$\text { Taking positive sign, } a=\frac{a+8}{5} \\ $
$\Rightarrow 5 a=a+8 \\ $
$\Rightarrow 4 a=8 \Rightarrow a=2 \\ $
$\text { Taking negative sign, } a=\frac{-a-8}{5} \\ $
$\Rightarrow 5 a=-a-8 \\ $
$\Rightarrow 6 a=-8 \Rightarrow a=-4 / 3 $
| But | $a \neq-4 / 3$ |
|---|---|
| $\because$ | $a=2$ |
So, the equation of circle is
$ \begin{aligned} & (x+2)^{2}+(y+2)^{2}=2^{2} \quad[\because a=2] \\ & \Rightarrow \quad x^{2}+4 x+4+y^{2}+4 y+4=4 \\ & \Rightarrow \quad x^{2}+y^{2}+4 x+4 y+4=0 \end{aligned} $
7. If one end of a diameter of the circle $x^{2}+y^{2}-4 x-6 y+11=0$ is $(3,4)$, then find the coordinates of the other end of the diameter.
Show Answer
Thinking Process
First of all get the centre of the circle from the given equation, then find the mid-point of the diameter of the circle.
Solution
Given equation of the circle is
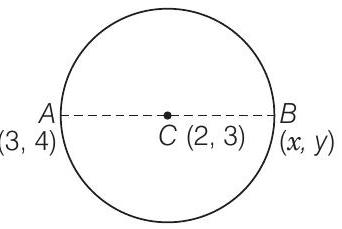
$ x^{2}+y^{2}-4 x-6 y+11=0 . $
$\therefore \quad 2 g=-4$ and $2 f=-6$
So, the centre of the circle is $(-g,-f)$ i.e., $(2,3)$.
Since, the mid-point of $A B$ is $(2,3)$.
Then,
$2=\frac{3+x_1}{2}$
$\Rightarrow$
$4=3+x_1$
$\therefore$
$x_1=1$
and
$\Rightarrow$
$3=\frac{4+y_1}{2}$
$6=4+y_1 \Rightarrow y_1=2$
So, the coordinates of other end of the diameter will be $(1,2)$.
8. Find the equation of the circle having $(1,-2)$ as its centre and passing through $3 x+y=14,2 x+5 y=18$.
Show Answer
Solution
Given that, centre of the circle is $(1,-2)$ and the circle passing through the lines
$ 3 x+y=14 $
and
$ 2 x+5 y=18 $
From Eq. (i) $y=14-3 x$ put in Eq. (ii), we get
$ \Rightarrow \quad \begin{aligned} & 2 x+70-15 x=18 \\ \Rightarrow & -13 x=-52 \Rightarrow x=4 \end{aligned} $
Now, $x=4$ put in Eq. (i), we get
$ 12+y=14 \Rightarrow y=2 $
Since, point $(4,2)$ lie on these lines also lies on the circle.
$ \begin{aligned} \therefore \quad \text { Radius of the circle } & =\sqrt{(4-1)^{2}+(2+2)^{2}} \\ & =\sqrt{9+16}=5 \end{aligned} $
Now, equation of the circle is
$(x-1)^{2}+(y+2)^{2} =5^{2} \\ $
$\Rightarrow x^{2}-2 x+1+y^{2}+4 y+4 =25 \\ $
$\Rightarrow x^{2}+y^{2}-2 x+4 y-20 =0 $
9. If the line $y=\sqrt{3} x+k$ touches the circle $x^{2}+y^{2}=16$, then find the value of $k$.
Show Answer
Solution
Given equation of circle,
$ x^{2}+y^{2}=16 $
$\therefore$ Radius $=4$ and centre $=(0,0)$
Now, perpendicular from $(0,0)$ to line $y=\sqrt{3} x+k=$ Radius of the circle
$|\frac{0-0+k}{\sqrt{3+1}}|=4$
Since the distance from the point $(m, n)$ to the line $A x+B y+k=0$ is $d=|\frac{A m+B n+C}{A^{2}+B^{2}}|$
$ \begin{matrix} \Rightarrow & \pm \frac{k}{2} & =4 \\ \therefore & k & = \pm 8 \end{matrix} $
10. Find the equation of a circle concentric with the circle $x^{2}+y^{2}-6 x+12 y+15=0$ and has double of its area.
Show Answer
Solution
Given equation of the circle is
$ \begin{aligned} & x^{2}+y^{2}-6 x+12 y+15=0 \\ & \therefore \quad 2 g=-6 \Rightarrow g=-3 \\ & \text { and } \\ & 2 f=12 \Rightarrow f=6 \\ & c=15 \end{aligned} $
[since, the circles are concentric]
Let radius of the required circle $=r_1$
$\therefore \quad 2 \times$ Area of the given circle $=$ Area of the required circle
$ \begin{matrix} \Rightarrow & 2[\pi(\sqrt{30})^{2}] & =\pi_1^{2} \\ \Rightarrow & 60 & =r_1^{2} \\ \Rightarrow & r_1 & =\sqrt{60} \\ \therefore & \sqrt{g^{2}+f^{2}-c} & =\sqrt{60} \\ \Rightarrow & 9+36-c & =60 \\ \Rightarrow & c & =-15 \end{matrix} $
So, the required equation of circle is $x^{2}+y^{2}-6 x+12 y-15=0$.
11. If the latusrectum of an ellipse is equal to half of minor axis, then find its eccentricity.
Show Answer
Solution
Consider the equation of the ellipse is $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$.
$\therefore$ Length of major axis $=2 a$
Length of minor axis $=2 b$
and length of latusrectum $=\frac{2 b^{2}}{a}$
Given that,
$ \begin{aligned} \frac{2 b^{2}}{a} & =\frac{2 b}{2} \\ a & =2 b \Rightarrow b=a / 2 \\ b^{2} & =a^{2}(1-e^{2}) \end{aligned} $
$\Rightarrow$
We know that,
$\Rightarrow$
$\frac{a}2^{2}=a^{2}(1-e^{2})$
$\Rightarrow \quad \frac{a^{2}}{4}=a^{2}(1-e^{2})$
$\Rightarrow \quad 1-e^{2}=\frac{1}{4}$
$\Rightarrow$
$e^{2}=1-\frac{1}{4}$
$e=\sqrt{\frac{3}{4}}=\sqrt{\frac{3}{2}}$
12. If the ellipse with equation $9 x^{2}+25 y^{2}=225$, then find the eccentricity and foci.
Show Answer
Thinking Process
Find the values of $a$ and $b$ by the given equation of ellipse, then use the formula $b^{2}=a^{2}(1-e^{2})$ to get the value of $e$.
Solution
Given equation of ellipse,
$ \begin{aligned} 9 x^{2}+25 y^{2} & =225 \\ \frac{x^{2}}{25}+\frac{y^{2}}{9} & =1 \\ a=5, b & =3 \\ b^{2} & =a^{2}(1-e^{2}) \\ 9 & =25(1-e^{2}) \\ \frac{9}{25} & =1-e^{2} \\ e^{2} & =1-9 / 25 \\ =\sqrt{1-9 / 25} & =\sqrt{\frac{25-9}{25}} \\ & =\sqrt{\frac{16}{25}}=4 / 5 \end{aligned} $
$ \begin{matrix} \Rightarrow & \frac{x^{2}}{25}+\frac{y^{2}}{9} & =1 \\ \Rightarrow & a=5, b & =3 \\ & \text { We know that, } & b^{2} & =a^{2}(1-e^{2}). \\ \Rightarrow & 9 & =25(1-e^{2}). \\ \Rightarrow & \frac{9}{25} & =1-e^{2} \\ \Rightarrow & e^{2} & =1-9 / 25 \\ & \therefore & e=\sqrt{1-9 / 25} & =\sqrt{\frac{25-9}{25}} \end{matrix} $
Foci $=( \pm a e, 0)=( \pm 5 \times 4 / 5,0)=( \pm 4,0)$
13. If the eccentricity of an ellipse is $\frac{5}{8}$ and the distance between its foci is 10 , then find latusrectum of the ellipse.
Show Answer
Solution
Given that, eccentricity $=\frac{5}{8}$, i.e., $e=\frac{5}{8}$
Let equation of the ellipse be $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$,
Since the foci of this ellipse is $( \pm a e, 0)$.
$\therefore \quad$ Distance between foci $=\sqrt{(a e+a e)^{2}}$
$\Rightarrow \quad 2 \sqrt{a^2 e^2}=10 \quad[\because$ distance between its foci $=10]$
$\Rightarrow \quad \sqrt{a^{2} e^{2}}=5$
$\Rightarrow \quad a^{2} e^{2}=25$
$\Rightarrow \quad a^{2}=\frac{25 \times 64}{25}$
$\therefore \quad a=8$
We know that,
$\Rightarrow$
$b^{2}=a^{2}(1-e^{2})$
$\Rightarrow \quad b^{2}=64 \quad 1-\frac{25}{64}$
$\Rightarrow \quad b^{2}=64 \frac{64-25}{64}$
$b^{2}=39$
$\therefore \quad$ Length of latusrectum of ellipse $=\frac{2 b^{2}}{a}=2 \quad \frac{39}{8}=\frac{39}{4}$
14. Find the equation of ellipse whose eccentricity is $\frac{2}{3}$, latusrectum is 5 and the centre is $(0,0)$.
Show Answer
Thinking Process
First of all find the values of $a$ and $b$ using the formula $b^{2}=a^{2}(1-e^{2})$, then get the equation of the ellipse.
Solution
Given that, $e=2 / 3$ and latusrectum $=5$
$ \begin{matrix} \text { i.e., } & \frac{2 b^{2}}{a}=5 \Rightarrow b^{2}=\frac{5 a}{2} \\ \text { We know that, } & \frac{b^{2}}{}=a^{2}(1-e^{2}) \\ \Rightarrow & \frac{5 a}{2}=a^{2} 1-\frac{4}{9} \\ \Rightarrow & \frac{5}{2}=\frac{5 a}{9} \Rightarrow a=9 / 2 \Rightarrow a^{2}=\frac{81}{4} \\ \Rightarrow & b^{2}=\frac{5 \times 9}{2 \times 2}=\frac{45}{4} \end{matrix} $
So, the required equation of the ellipse is $\frac{4 x^{2}}{81}+\frac{4 y^{2}}{45}=1$.
15. Find the distance between the directrices of ellipse $\frac{x^{2}}{36}+\frac{y^{2}}{20}=1$.
Show Answer
Solution
The equation of ellipse is $\frac{x^{2}}{36}+\frac{y^{2}}{20}=1$.
On comparing this equation with $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$, we get
We know that,
$a=6, b=2 \sqrt{5}$
$\Rightarrow$
$b^{2}=a^{2}(1-e^{2})$
$\Rightarrow \quad \frac{20}{36}=1-e^{2}$
$20=36(1-e^{2})$
$\therefore \quad e=\sqrt{1-\frac{20}{36}}=\sqrt{\frac{16}{36}}$
$E=\frac{4}{6}=\frac{2}{3}$
Now,
$\therefore \quad \frac{a}{e}=\frac{\frac{6}{2}}{3}=\frac{6 \times 3}{2}=9$
and
$ -\frac{a}{e}=-9 $
$\therefore$ Distance between the directrices $=|9-(-9)|=18$
16. Find the coordinates of a point on the parabola $y^{2}=8 x$, whose focal distance is 4.
Thinking Process
The distance of a point $(h, k)$ from the focus $S$ is called the focal distance of the point $P$. The focal distance of any point $P(h, k)$ on the parabola $y^{2}=4 a x$ is $|h+a|$.
Show Answer
Solution
Given parabola is $y^{2}=8 x$
On comparing this parabola to the $y^{2}=4 a x$, we get
$ 8 x=4 a x \Rightarrow a=2 $
$\therefore$ Focal distance $=|x+a|=4$
$ \begin{matrix} \Rightarrow & |x+2| & =4 \\ \Rightarrow & x+2 & = \pm 4 \\ \Rightarrow & x & =2,-6 \\ \text { But } & x & \neq-6 \\ \text { For } x=2, & y^{2} & =8 \times 2 \\ \therefore & y^{2} & =16 \Rightarrow y= \pm 4 \end{matrix} $
So, the points are $(2,4)$ and $(2,-4)$.
17. Find the length of the line segment joining the vertex of the parabola $y^{2}=4 a x$ and a point on the parabola, where the line segment makes an angle $\theta$ to the $X$-axis.
Show Answer
Solution
Given equation of the parabola is $y^{2}=4 a x$
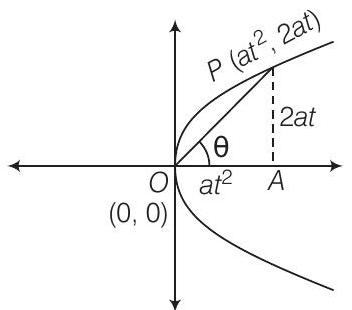
Let the coordinates of any point $P$ on the parabola be $(a t^{2}, 2 a t)$.
$ \begin{aligned} & \text { In } \triangle P O A, \quad \tan \theta=\frac{2 \text { at }}{a t^{2}}=\frac{2}{t} \\ & \Rightarrow \quad \tan \theta=\frac{2}{t} \Rightarrow t=2 \cot \theta \\ & \therefore \quad \quad \text { length of } O P=\sqrt{(0-a t^{2})^{2}+(0-2 a t)^{2}} \\ & =\sqrt{a^{2} t^{4}+4 a^{2} t^{2}} \\ & =a t \sqrt{t^{2}+4} \\ & =2 a \cot \theta \sqrt{4 \cot ^{2} \theta+4} \\ & =4 a \cot \theta \sqrt{1+\cot ^{2} \theta} \\ & =4 a \cot \theta \cdot cosec \theta \\ & =\frac{4 a \cos \theta}{\sin \theta} \cdot \frac{1}{\sin \theta}=\frac{4 a \cos \theta}{\sin ^{2} \theta} \end{aligned} $
18. If the points $(0,4)$ and $(0,2)$ are respectively the vertex and focus of a parabola, then find the equation of the parabola.
Show Answer
Solution
Given that the coordinates, vertex of the parabola $(0,4)$ and focus of the parabola $(0,2)$.
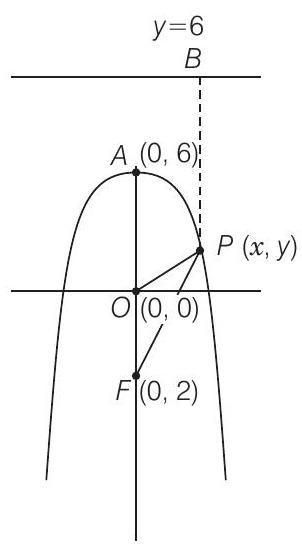
By definition of the parabola, $\quad P B=P F$
$ \begin{matrix} \Rightarrow & & |\frac{0+y-6}{\sqrt{0+1}}| & =\sqrt{(x-0)^{2}+(y-2)^{2}} \\ \Rightarrow & & |y-6| & =\sqrt{x^{2}+y^{2}-4 y+4} \\ \Rightarrow & & x^{2}+y^{2}-4 y+4 & =y^{2}+36-12 y \\ \Rightarrow & x^{2}+8 y & =32 \end{matrix} $
19. If the line $y=m x+1$ is tangent to the parabola $y^{2}=4 x$, then find the value of $m$.
Show Answer
Solution
Given that, line $y=m x+1$ is tangent to the parabola $y^{2}=4 x$. $\therefore$
and
$ \begin{aligned} y & =m x+1 \\ y^{2} & =4 x \end{aligned} $
From Eqs. (i) and (ii),
$ \begin{matrix} \Rightarrow & m^{2} x^{2}+2 m x+1 & =4 x \\ \Rightarrow & & m^{2} x^{2}+2 m x-4 x+1 & =0 \\ \Rightarrow & m^{2} x^{2}+x(2 m-4)+1 & =0 \\ \Rightarrow & (2 m-4)^{2}-4 m^{2} \times 1 & =0 \\ \Rightarrow & 4 m^{2}+16-16 m-4 m^{2} & =0 \\ \therefore & 16 m & =16 \\ & m & =1 \end{matrix} $
20. If the distance between the foci of a hyperbola is 16 and its eccentricity is $\sqrt{2}$, then obtain the equation of the hyperbola.
Show Answer
Thinking Process
First of all find the value of $a$ and $b$ using the given condition, then put them in $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ to get the required equation of the hyperbola.
Solution
Distance between the foci i.e., and
$ \begin{aligned} 2 a e & =16 \Rightarrow a e=8 \\ e & =\sqrt{2} \\ a \sqrt{2} & =8 \\ a & =4 \sqrt{2} \\ b^{2} & =a^{2}(e^{2}-1) \\ b^{2} & =(4 \sqrt{2})^{2}[(\sqrt{2})^{2}-1] \\ & =16 \times 2(2-1) \\ & =32(2-1) \end{aligned} $
$ \text { and } $
We know that,
$\Rightarrow$
So, the equation of hyperbola is
$ \begin{aligned} & \frac{x^{2}}{32}-\frac{y^{2}}{32}=1 \\ & \Rightarrow \quad x^{2}-y^{2}=32 \end{aligned} $
21. Find the eccentricity of the hyperbola $9 y^{2}-4 x^{2}=36$.
Show Answer
Solution
Given equation of the hyperbola is
$ \begin{matrix} \Rightarrow & & 9 y^{2}-4 x^{2} & =36 \\ \Rightarrow & \frac{9 y^{2}}{36}-\frac{4 x^{2}}{36} & =\frac{36}{36} \\ \Rightarrow & \frac{y^{2}}{4}-\frac{x^{2}}{9} & =1 \\ \Rightarrow & -\frac{x^{2}}{9}+\frac{y^{2}}{4} & =1 \end{matrix} $
Since, this equation in form of $-\frac{x^{2}}{a}+\frac{y^{2}}{b^{2}}=1$, where $a=3$ and $b=2$.
$ \begin{aligned} \therefore \quad e & =\sqrt{1+\frac{a}b^{2}} \\ & =\sqrt{1+\frac{9}{4}}=\frac{\sqrt{13}}{2} \end{aligned} $
22. Find the equation of the hyperbola with eccentricity $\frac{3}{2}$ and foci at $( \pm 2,0)$.
Show Answer
Solution
Given that eccentricity i.e., $e=3 / 2$ and $( \pm a e, 0)=( \pm 2,0)$
$ \begin{aligned} \therefore a e & =2 \\ \Rightarrow a \cdot \frac{3}{2} & =2 \Rightarrow a=4 / 3 \\ \because b^{2} & =a^{2}(e^{2}-1) \\ \Rightarrow b^{2} & =\frac{16}{9} \quad \frac{9}{4}-1 \\ \Rightarrow b^{2} & =\frac{16}{4} \quad \frac{5}{4}=+\frac{20}{9} \end{aligned} $
So, the equation of hyperbola is
$\quad \frac{x^2}{\frac{16}{9}}-\frac{y^2}{\frac{20}{9}}=1$
$\Rightarrow \frac{x^2}{4}-\frac{y^2}{5}=\frac{4}{9}$
Long Answer Type Questions
23. If the lines $2 x-3 y=5$ and $3 x-4 y=7$ are the diameters of a circle of area 154 square units, then obtain the equation of the circle.
Show Answer
Thinking Process
First of all find the intersection point of the given lines, then get radius of circle from given area. Now, use formula equation of circle with centre $(h, k)$ and radius a is $(x-h)^{2}+$ $(y-k)^{2}=a^{2}$.
Solution
Given lines are
and
$ \begin{aligned} 2 x-3 y-5 & =0 \\ 3 x-4 y-7 & =0 \\ \frac{x}{21-20} & =\frac{y}{-15+14}=\frac{1}{-8+9} \\ \frac{x}{1} & =\frac{y}{-1}=\frac{1}{+1} \\ x & = \pm 1, y=-1 \end{aligned} $
Since the intersection point of these lines will be coordinates of the circle i.e., coordinates of the circle as $(1,-1)$.
Let the radius of the circle is $r$.
Then
$ \pi r^{2}=154 $
$ \begin{aligned} \Rightarrow & \frac{22}{7} \times r^{2} & =154 \\ \Rightarrow & r^{2} & =\frac{154 \times 7}{22} \\ \Rightarrow & r^{2} & =\frac{14 \times 7}{2} \Rightarrow r^{2}=49 \end{aligned} $
So, the equation of circle is
$ (x-1)^{2}+(y+1)^{2}=49 $
$ \begin{matrix} \Rightarrow & x^{2}-2 x+1+y^{2}+2 y+1=49 \\ \Rightarrow & x^{2}+y^{2}-2 x+2 y=47 \end{matrix} $
24. Find the equation of the circle which passes through the points $(2,3)$ and $(4,5)$ and the centre lies on the straight line $y-4 x+3=0$.
Show Answer
Solution
Let the general equation of the circle is
$ x^{2}+y^{2}+2 g x+2 f y+c=0 $
Since, this circle passes through the points $(2,3)$ and $(4,5)$.
$ \begin{matrix} \therefore & 4+9+4 g+6 f+c & =0 \\ \Rightarrow & 4 g+6 f+c & =-13 \\ \text { and } & 16+25+8 g+10 f+c & =0 \\ \Rightarrow & 8 g+10 f+c & =-41 \end{matrix} $
Since, the centre of the circle $(-g,-f)$ lies on the straight line $y-4 x+3=0$
i.e., $\quad+4 g-f+3=0$
From Eq. (iv), $4 g=f-3$
On putting $4 g=f-3$ in Eq. (ii), we get
$ f-3+6 f+c=-13 $
$ \Rightarrow \quad 7 f+c=10 $
From Eqs. (ii) and (iii),
$ \begin{gathered} 8 g+12 f+2 c=-26 \\ 8 g+10 f+c=-41 \\ -\quad-\quad+ \\ \hline 2 f+c=15 \end{gathered} $
From Eqs. (ii) and (vi),
$ \begin{aligned} & 7 f+c=-10 \\ & 2 f+c=15 \\ & \frac{–}{5 f=-25} \\ & \therefore \quad f=-5 \\ & \text { Now, } \quad c=10+15=25 \\ & \text { From Eq. (iv), } \quad 4 g+5+3=0 \\ & \Rightarrow \quad g=-2 \\ & \text { From Eq. (i), equation of the circle is } x^{2}+y^{2}-4 x-10 y+25=0 \text {. } \end{aligned} $
25. Find the equation of a circle whose centre is $(3,-1)$ and which cuts off a chord 6 length 6 units on the line $2 x-5 y+18=0$.
Show Answer
Solution
Given centre of the circle is $(3,-1)$.
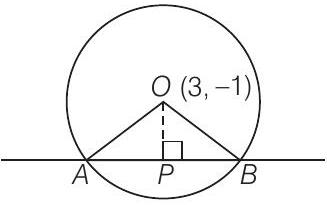
Now,
$ O P=|\frac{6+5+18}{\sqrt{4+25}}|=\frac{29}{\sqrt{29}}=\sqrt{29} $
$\ln \triangle O P B$
$ \begin{matrix} O B^{2}=O P^{2}+P B^{2} & {[\because A B=6 \Rightarrow P B=3]} \\ O B^{2}=29+9 \Rightarrow O B^{2}=38 \end{matrix} $
$\Rightarrow$
So, the radius of circle is $\sqrt{38}$,
$\therefore$ Equation of the circle with radius $r=\sqrt{38}$ and centre $(3,-1)$ is
$\Rightarrow \quad(x-3)^{2}+(y+1)^{2}=38$
$\Rightarrow \quad x^{2}-6 x+9+y^{2}+2 y+1=38$
$x^{2}+y^{2}-6 x+2 y=28$
26. Find the equation of a circle of radius 5 which is touching another circle $x^{2}+y^{2}-2 x-4 y-20=0$ at $(5,5)$.
Show Answer
Solution
Let the coordinates of centre of the required circle are $(h, k)$, then the centre of another circle is $(1,2)$
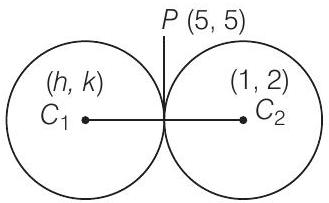 Radius $=\sqrt{1+4+20}=5$
Radius $=\sqrt{1+4+20}=5$
Conic Sections
So, it is clear that $P$ is the mid-point of $C_1 C_2$.
$\begin{matrix} \therefore & 5=\frac{1+h}{2} \Rightarrow h=9 \\ \text { and } & 5=\frac{2+k}{2} \Rightarrow k=8\end{matrix} $
So, the equation of and required circle is
$(x-9)^{2}+(y-8)^{2} =25 \\ $
$\Rightarrow x^{2}-18 x+81+y^{2}-16 y+64 =25 \\ $
$\Rightarrow x^{2}+y^{2}-18 x-16 y+120 =0 $
27. Find the equation of a circle passing through the point $(7,3)$ having radius 3 units and whose centre lies on the line $y=x-1$.
Show Answer
Thinking Process
First of all let the equation of a circle with centre $(h, k)$ and radius $r$ is
$(x-h)^{2}+(y-h)^{2}=r^{2}$, then we get the value of $(h, k)$ using given condition.
Solution
Let equation of circle be
$(x-h)^{2}+(y-k)^{2}=r^{2} \\ $
$\Rightarrow (x-h)^{2}+(y-k)^{2}=9 $
$ y=x-1 i . e ., k=h-1 $
Now, the circle passes through the point $(7,3)$.
$ \begin{matrix} \therefore & (7-h)^{2}+(3-k)^{3}=9 \\ \Rightarrow & 49-14 h+h^{2}+9-6 k+k^{2}=9 \\ \Rightarrow & h^{2}+k^{2}-14 h-6 k+49=0 \end{matrix} $
On putting $k=h-1$ in Eq. (iii), we get
$ h^{2}+(h-1)^{2}-14 h-6(h-1)+49=0 $
$ \begin{matrix} \Rightarrow & h^{2}+h^{2}-2 h+1-14 h-6 h+6+49=0 \\ \Rightarrow & 2 h^{2}-22 h+56=0 \\ \Rightarrow & h^{2}-11 h+28=0 \\ \Rightarrow & h^{2}-7 h-4 h+28=0 \\ \Rightarrow & h(h-7)-4(h-7)=0 \end{matrix} $
$\Rightarrow$
$ (h-7)(h-4)=0 $
$\therefore$
When
$\therefore$ Centre $(7,6)$
When $\quad h=4$, then $k=3$
$\therefore$ Centre $-(4,3)$
So, the equation of circle when centre $(7,6)$, is
$ \begin{matrix} \Rightarrow & x^{2}-14 x+49+y^{2}-12 y+36=9 \\ \Rightarrow & x^{2}+y^{2}-14 x-12 y+76=0 \end{matrix} $
$ (x-7)^{2}+(y-6)^{2}=9 $
When centre $(4,3)$, then the equation of the circle is
$ (x-4)^{2}+(y-3)^{2}=9 $
$\Rightarrow$
$ x^{2}-8 x+16+y^{2}-6 y+9=9 $
$\Rightarrow$
$ x^{2}+y^{2}-8 x-6 y+16=0 $
28. Find the equation of each of the following parabolas
(i) directrix $=0$, focus at $(6,0)$
(ii) vertex at $(0,4)$, focus at $(0,2)$
(iii) focus at $(-1,-2)$, directrix $x-2 y+3=0$
Show Answer
Solution
(i) Given that, directrix $=0$ and focus $=(6,0)$
So, the equation of the parabola
$ (x-6)^{2}+y^{2}=x^{2} $
$ \begin{matrix} \Rightarrow & x^{2}+36-12 x+y^{2}=x^{2} \\ \Rightarrow & y^{2}-12 x+36=0 \end{matrix} $
(ii) Given that, vertex $=(0,4)$ and focus $=(0,2)$
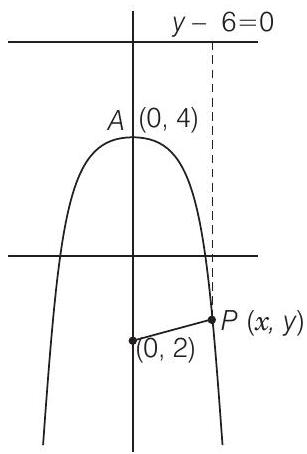
So, the equation of parabola is
$\sqrt{(x-0)^{2}+(y-2)^{2}} =|y-6| \\ $
$\Rightarrow x^{2}+y^{2}-4 y+4 =y^{2}-12 y+36 \\ $
$\Rightarrow x^{2}-4 y+12 y-32 =0 \\ $
$\Rightarrow x^{2}+8 y-32 =0 \\ $
$\Rightarrow x^{2} =32-8 y $
(iii) Given that, focus at $(-1,-2)$ and directrix $x-2 y+3=0$
So, the equation of parabola is $\sqrt{(x+1)^{2}+(y+2)^{2}}=|\frac{x-2 y+3}{\sqrt{1+4}}|$
$ \begin{matrix} \Rightarrow & x^{2}+2 x+1+y^{2}+4 y+4=\frac{1}{5}[x^{2}+4 y^{2}+9-4 x y-12 y+6 x] \\ \Rightarrow & 4 x^{2}+4 x y+y^{2}+4 x+32 y+16=0 \end{matrix} $
29. Find the equation of the set of all points the sum of whose distances from the points $(3,0),(9,0)$ is 12.
Show Answer
Solution
Let the coordinates of the point be $(x, y)$, then according to the question,
$\sqrt{(x-3)^{2}+y^{2}}+\sqrt{(x-9)^{2}+y^{2}}=12 \\ $
$\Rightarrow \sqrt{(x-3)^{2}+y^{2}}=12-\sqrt{(x-9)^{2}+y^{2}} $
Conic Sections
On squaring both sides, we get
$ x^{2}-6 x+9+y^{2} =144+(x^{2}-18 x+81+y^{2})-24 \sqrt{(x-9)^{2}+y^{2}} \\ $
$\Rightarrow 12 x-216 =-24 \sqrt{(x-9)^{2}+y^{2}} \\ $
$\Rightarrow x-18 =-2 \sqrt{(x-9)^{2}+y^{2}} \\ $
$\Rightarrow x^{2}-36 x+324 =4(x^{2}-18 x+81+y^{2}) \\ $
$3 x^{2}+4 y^{2}-36 x =0 $
30. Find the equation of the set of all points whose distance from $(0,4)$ are $\frac{2}{3}$ of their distance from the line $y=9$.
Show Answer
Thinking Process
Consider the points $(x, y)$, and apply the condition given in the problem, then get the set of all points.
Solution
Let the point be $P(x, y)$.
$\therefore$ Distance from $(0,4)=\sqrt{x^{2}+(y-4)^{2}}$
So, the distance from the line $y=9$ is $|\frac{y-9}{\sqrt{1}}|$
$ \begin{matrix} \therefore & \sqrt{x^{2}+(y-4)^{2}}=\frac{2}{3}|\frac{y-9}{1}| \\ \Rightarrow & x^{2}+y^{2}-8 y+10=\frac{4}{9}(y^{2}-18 y+81) \\ \Rightarrow & 9 x^{2}+9 y^{2}-72 y+144=4 y^{2}-72 y+324 \\ \Rightarrow & 9 x^{2}+5 y^{2}=180 \end{matrix} $
31. Show that the set of all points such that the difference of their distances from $(4,0)$ and $(-4,0)$ is always equal to 2 represent a hyperbola.
Show Answer
Solution
Let the points be $P(x, y)$
$\therefore$ Distance of $P$ from $(4,0) \sqrt{(x-4)^{2}+y^{2}}$
and the distance of $P$ from $(-4,0) \sqrt{(x+4)^{2}+y^{2}}$
Now,
$ \begin{aligned} & \sqrt{(x+4)^{2}+y^{2}}-\sqrt{(x-4)^{2}+y^{2}}=2 \\ & \sqrt{(x+4)^{2}+y^{2}}=2+\sqrt{(x-4)^{2}+y^{2}} \end{aligned} $
$\Rightarrow$
On squaring both sides, we get
$x^{2}+8 x+16+y^{2} =4+x^{2}-8 x+16+y^{2}+4 \sqrt{(x-4)^{2}+y^{2}} \\ $
$\Rightarrow 16 x-4 =4 \sqrt{(x-4)^{2}+y^{2}} \\ $
$\Rightarrow 4(4 x-1) =4 \sqrt{(x-4)^{2}+y^{2}} \\ $
$\Rightarrow 16 x^{2}-8 x+1 =x^{2}+16-8 x+y^{2} \\ $
$15x^{2}-y^{2} =15 \text { which is a parabola. } $
32. Find the equation of the hyperbola with
(i) Vertices $( \pm 5,0)$, foci $( \pm 7,0)$
(ii) Vertices $(0, \pm 7), e=\frac{7}{3}$.
(iii) Foci $(0, \pm \sqrt{10})$, passing through $(2,3)$.
Show Answer
Solution
(i) Given that, vertices $=( \pm 5,0)$, foci $=( \pm 7,0)$ and $a= \pm 5$
$ \begin{matrix} \therefore & ( \pm a e, 0)=( \pm 7,0) \\ \text { Now } & a e=7 \Rightarrow 5 e=7 \\ \Rightarrow & e=7 / 5 \\ \because & b^{2}=a^{2}(e^{2}-1) \\ \Rightarrow & b^{2}=25 \frac{49}{25}-1 \\ \Rightarrow & b^{2}=25 \frac{49-25}{25} \\ \Rightarrow & b^{2}=24 \end{matrix} $
So,the equation of parabola is
$ \frac{x^{2}}{25}-\frac{y^{2}}{24}=1 \quad[\because a^{2}=25 \text { and } b^{2}=24] $
(ii) Vertices $=(0, \pm 7), e=4 / 3$
$ \begin{matrix} \therefore & b & =7, e=4 / 3 \\ & \ddots & e^{2} & =1+\frac{a^{2}}{b^{2}} \\ \Rightarrow & & \frac{16}{9}-1 & =\frac{a^{2}}{49} \\ \Rightarrow & & \frac{7}{9} & =\frac{a^{2}}{49} \Rightarrow a^{2}=\frac{343}{9} \end{matrix} $
So, the equation of hyperbola is
$-\frac{x^{2} \times 9}{343}+\frac{y^{2}}{49} =1 \\ $
$\Rightarrow -\frac{9 x^{2}}{7}+y^{2} =49 \\ $
$\Rightarrow 9 x^{2}-7 y^{2}+343 =0 $
(iii) Given that, foci $=(0, \pm \sqrt{10})$
$ \begin{aligned} \because & b e & =\sqrt{10} \\ \Rightarrow & a^{2}+b^{2} & =10 \\ \Rightarrow & a^{2} & =10-b^{2} \end{aligned} $
$\therefore$ Equation of the hyperbola be
$ -\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 $
Since, this hyperbola passes through the point $(2,3)$.
$ \begin{matrix} \therefore & -\frac{4}{a^{2}}+\frac{9}{b^{2}}=1 \\ \Rightarrow & \frac{-4}{10-b^{2}}+\frac{9}{b^{2}}=1 \end{matrix} $
$ \begin{matrix} \Rightarrow & \frac{-4 b^{2}+90-9 b^{2}}{b^{2}(10-b^{2})}=1 \\ \Rightarrow & -13 b^{2}+90=10 b^{2}+b^{4} \\ \Rightarrow & b^{4}-23 b^{2}+90=0 \\ \Rightarrow & b^{4}-18 b^{2}-5 b^{2}+90=0 \\ \Rightarrow & b^{2}(b^{2}-18)-5(b^{2}-18)=0 \\ \Rightarrow & (b^{2}-18)(b^{2}-5)=0 \\ \Rightarrow & b^{2}=18 \Rightarrow b= \pm 3 \sqrt{2} \\ \text { or } & b^{2}=5 \Rightarrow b=\sqrt{5} \\ \therefore & b^{2}=18 \text { then } a^{2}=-8 \\ \text { When } & a^{2}=5 \text {, then } b^{2}=5 \end{matrix} $
$ \therefore \quad b^{2}=18 \text { then } a^{2}=-8 \quad \text { [not possible] } $
So, the equation of hyperbola is
$\Rightarrow -\frac{x^{2}}{5}+\frac{y^{2}}{5} =1 \\ $
$\Rightarrow y^{2}-x^{2} =5 $
True/False
33. The line $x+3 y=0$ is a diameter of the circle $x^{2}+y^{2}+6 x+2 y=0$.
Show Answer
Thinking Process
If a line is the diameter of circle, then the centre of the circle should lies on line. Use this property to solve the given problem.
Solution
False
Given equation of the circle is
$ \begin{matrix} \therefore & x^{2}+y^{2}+6 x+2 y & =0 \\ \text { Since given line is } x+3 y=0 . & & \text { Centre }=(-3,-1) \\ \Rightarrow \quad & -3-3 & \neq 0 \end{matrix} $
So, this line is not diameter of the circle.
34. The shortest distance from the point $(2,-7)$ to the circle $x^{2}+y^{2}-14 x-10 y-151=0$ is equal to 5 .
Show Answer
Solution
False
Given circle is $x^{2}+y^{2}-14 x-10 y-151=0$.
$\therefore \quad$ Centre $=(7,5)$
and $\quad$ Radius $=\sqrt{49+25+151}=\sqrt{225}=15$
So, the distance between the point $(2,-7)$ and centre of the circle is given by
$\therefore$ Shortest distance, $d=|13-15|=2$
$ \begin{aligned} d_1 & =\sqrt{(2-7)^{2}+(-7-5)^{2}} \\ & =\sqrt{25+144}=\sqrt{169}=13 \end{aligned} $
35. If the line $l x+m y=1$ is a tangent to the circle $x^{2}+y^{2}=a^{2}$, then the point $(l, m)$ lies on a circle.
Show Answer
Solution
True
Given circle is $x^{2}+y^{2}=a^{2}$
$\therefore$ Radius of circle $=a$ and centre $=(0,0)$
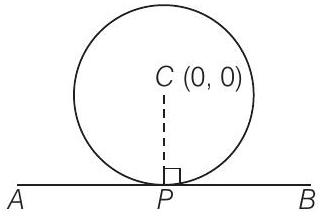
$\therefore$ Distance from point $(l, m)$ and centre is $\sqrt{(0-e)^{2}+(0-m)^{2}}=a$
$\Rightarrow \quad l^{2}+m^{2}=a^{2}$
So, $l, m$ lie on the circle.
36. The point $(1,2)$ lies inside the circle $x^{2}+y^{2}-2 x+6 y+1=0$.
Show Answer
Thinking Process
If the $x_1, y_1$ lies inside the circle $S \equiv x^{2}+y^{2}+2 g x+2 f y+c=0$, then $x_1^{2}+y_1^{2}+2 g x_1+2 f y_1+c<0$ and it $S>0$, then the point lies outside the circle.
Solution
False
Given circle is $S \equiv x^{2}+y^{2}-2 x+6 y+1=0$.
Since, the point is $(1,2)$.
Now,
$ \begin{gathered} S_1 \equiv 1+4-2+12+1 \\ S_1>0 \end{gathered} $
$\Rightarrow$
So, the $(1,2)$ lies outside the circle.
37. The line $l x+m y+n=0$ will touch the parabola $y^{2}=4 a x$, if In $=a m^{2}$.
Show Answer
Solution
True
Given equation of a line is
and
$l x+m y+n=0 \\ $
$\text { parabola } y^{2}=4 a x $
From Eq. (i), $x=-\frac{m y+n}{l}$ put in Eq. (ii), we get
$y^{2} =-\frac{4 a(m y+n)}{l} \\ $
$\Rightarrow l y^{2} =-4 a m y-4 a x \\ $
$\Rightarrow l y^{2}+4 a m y+4 a n =0 \\ $
$\text { For tangent, } D =0 \\ $
$\Rightarrow 16 a^{2} m^{2} =4 l \times 4 a n \\ $
$\Rightarrow 16 a^{2} m^{2} =16 \text { anl } \\ $
$\Rightarrow a m^{2} =n l $
38. If $P$ is a point on the ellipse $\frac{x^{2}}{16}+\frac{y^{2}}{25}=1$ whose foci are $S$ and $S^{\prime}$, then $P S+P S^{\prime}=8$.
Show Answer
Solution
False
Given equation of the ellipse is $\frac{x}{16}+\frac{y^{2}}{25}=1$.
which is in form of $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$, where $b>a$
$ \begin{aligned} & \therefore \quad \text { Foci, } S=(0, b e), S^{\prime}(0,-b e) \\ & \therefore \quad e=\sqrt{1-\frac{a^{2}}{b^{2}}} \\ & =\sqrt{\frac{25-16}{25}}=3 / 5 \end{aligned} $
$ \text { Foci, } S=0, \frac{3 \times 5}{5}, S^{\prime}=0,-\frac{3 \times 5}{5} \text { i.e., } S=(0,3), S^{\prime}=(0,-3) $
Let the coordinate of point $P$ be $(x, y)$ then $P S+P S^{\prime}=2 b=2 \times 5=10$
39. The line $2 x+3 y=12$ touches the ellipse $\frac{x^{2}}{9}+\frac{y^{2}}{4}=2$ at the point $(3,2)$.
Show Answer
Solution
True
Given equation of line is
and
$ \begin{aligned} 2 x+3 y & =12 \\ \text { ellipse } \frac{x^{2}}{9}+\frac{y^{2}}{4} & =2 \end{aligned} $
Since, the equation of tangent at $(x_1, y_1)$ is $\frac{x x_1}{9}+\frac{y y_1}{4}=2$.
$\therefore$ Tangent at $(3,2)$,
$ \begin{aligned} & & \frac{3 x}{9}+\frac{2 y}{4}=2 \\ \Rightarrow & \frac{x}{3}+\frac{y}{2} & =2 \\ \Rightarrow & 2 x+3 y & =12 \text {, which is a given line. } \end{aligned} $
Hence, the statement is true.
40. The locus of the point of intersection of lines $\sqrt{3} x-y-4 \sqrt{3 k}=0$ and $\sqrt{3} k x+k y-4 \sqrt{3}=0$ for different value of $k$ is a hyperbola whose eccentricity is 2.
Show Answer
Thinking Process
First of all eliminate $k$ from the given equations of line, then get the equation of hyperbola.
Solution
True
Given equations of line are
and
From Eq. (i),
$ \begin{aligned} \sqrt{3} x-y-4 \sqrt{3} k & =0 \\ \sqrt{3} k x+k y-4 \sqrt{3} & =0 \\ 4 \sqrt{3} k & =\sqrt{3} x-y \end{aligned} $
$ \begin{matrix} \Rightarrow & k=\frac{\sqrt{3} x-y}{4 \sqrt{3}} \text { put in Eq. (ii), we get } \\ \Rightarrow & \sqrt{3} x \frac{\sqrt{3} x-y}{4 \sqrt{3}}+\frac{\sqrt{3} x-y}{4 \sqrt{3}} y-4 \sqrt{3}=0 \\ \Rightarrow & \frac{1}{4}(\sqrt{3} x^{2}-x y)+\frac{1}{4} x y-\frac{y^{2}}{\sqrt{3}}-4 \sqrt{3}=0 \\ \Rightarrow & \frac{\sqrt{3}}{4} x^{2}-\frac{y^{2}}{4 \sqrt{3}}-4 \sqrt{3}=0 \\ \Rightarrow & 3 x^{2}-y^{2}-48=0 \\ \Rightarrow & 3 x^{2}=48, \text { which is a hyperbola. } \end{matrix} $
Fillers
41. The equation of the circle having centre at $(3,-4)$ and touching the line $5 x+12 y-12=0$ is ……
Show Answer
Solution
The perpendicular distance from centre $(3,-4)$ to the line is, $d=|\frac{\mid 5-48-12}{\sqrt{25+144}}|=\frac{45}{13}$
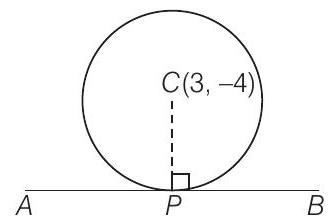
So, the required equations of the circle is $(x-3)^{2}+(y+4)^{2}=\frac{45}13^{2}$.
42. The equation of the circle circumscribing the triangle whose sides are the lines $y=x+2,3 y=4 x, 2 y=3 x$ is ……
Show Answer
Solution
Given equations of line are
From Eqs. (i) and (ii),
$ \begin{aligned} y & =x+2 \\ 3 y & =4 x \\ 2 y & =3 x \end{aligned} $
$\Rightarrow$
$ \frac{4 x}{3}=x+2 $
$\Rightarrow x=6$
On putting $x=6$ in Eq. (i), we get
$ \begin{aligned} & y & =8 \\ \therefore & \text { Point, } A & =(6,8) \end{aligned} $
From Eqs. (i) and (iii),
$ \begin{aligned} & \frac{3 x}{2}=x+2 \\ & 3 x=2 x+4 \Rightarrow x=4 \end{aligned} $
When
$\therefore$
From Eqs. (ii) and (iii)
Now,
Let the equation of circle is
$ \begin{aligned} x & =4, \text { then } y=6 \\ \text { Point, } B & =(4,6) \\ x_1 & =0_1, y=0 \\ C & =(0,0) \end{aligned} $
$ x^{2}+y^{2}+2 g x n+2 f y+c=0 $
Since, the points $A(6,8), B(4,6)$ and $C(0,0)$ lie on this circle.
$ 36+64+12 g+16 f+c=0 $
$ \begin{aligned} \Rightarrow & 12 g+16 f+c & =-100 \\ \text { and } & 16+36+8 g+12 f+c & =0 \\ \Rightarrow & 8 g+12 f+c & =-52 \\ \Rightarrow & c & =0 \end{aligned} $
From Eqs. (iv), (v) and (vi),
$ \begin{aligned} \Rightarrow & 12 g+16 f & =-100 \\ \Rightarrow & 3 g+4 f+25 & =0 \\ \Rightarrow & \frac{g}{+52-75} & =\frac{f}{50-39}=\frac{1}{9-8} \\ \Rightarrow & \frac{g}{-23} & =\frac{f}{11}=\frac{1}{1} \\ \Rightarrow & g & =-23, f=11 \end{aligned} $
So, the equation of circle is
$ \Rightarrow \quad \begin{aligned} x^{2}+y^{2}-46 x+22 y+0 & =0 \\ x^{2}+y^{2}-46 x+22 y & =0 \end{aligned} $
43. An ellipse is described by using an endless string which is passed over two pins. If the axes are $6 cm$ and $4 cm$, the length of the string and distance between the pins are ……
Show Answer
Solution
Let equation of the ellipse be $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$.
$ \begin{aligned} & \therefore \quad 29=6 \text { and } 2 b=4 \\ & \Rightarrow \\ & a=3 \text { and } b=2 \end{aligned} $
We know that,
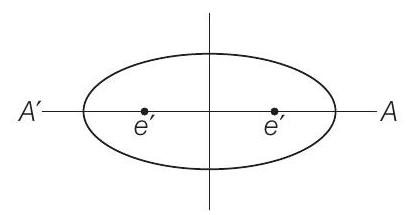
$ \begin{aligned} c^{2} & =a^{2}-b^{2}=(3)^{2}-(2)^{2} \\ & =9-4=5 \Rightarrow c=\sqrt{5} \end{aligned} $
$ \begin{aligned} \therefore \quad \text { Length of string } & =A C^{\prime}+C^{\prime} C+A C \\ & =a+c+2 c+a c \\ & =2 a+2 c=6+2 \sqrt{5} \end{aligned} $
$\therefore \quad$ Distances between the pins $=2 \sqrt{5}=C c^{\prime}$
44. The equation of the ellipse having foci $(0,1),(0,-1)$ and minor axis of length 1 is ……
Show Answer
Thinking Process
First of all get the value of $a$ and $b$ with the help of given condition in the problem, then we get the required equation of the ellipse.
Solution
Given that, foci of the ellipse are $(0, \pm b e)$.
$\because \quad$ be $\equiv 1$
$\therefore \quad$ Length of minor axis, $2 a=1 \Rightarrow a=1 / 2$
$ \begin{matrix} e^{2} & =1-\frac{a^{2}}{b^{2}} \\ \Rightarrow & (b e)^{2} & =b^{2}-a^{2} \Rightarrow 1=b^{2}-\frac{1}{4} \\ \Rightarrow & 1+\frac{1}{4} & =b^{2} \Rightarrow \frac{5}{4}=b^{2} \end{matrix} $
So, the equation of ellipse is
$ \frac{x^{2}}{\frac{1}{4}}+\frac{y^{2}}{5 / 4}=1 \Rightarrow \frac{4 x^{2}}{1}+\frac{4 y^{2}}{5}=1 $
45. The equation of the parabola having focus at $(-1,-2)$ and directrix is $x-2 y+3=0$, is ……
Show Answer
Solution
Given that, focus at $F(-1,-2)$ and directrix is $x-2 y+3=0$
Let any point on the parabola be $(x, y)$.
$ \begin{aligned} & \therefore \quad P F=|\frac{x-2 y+3}{\sqrt{1+4}}| \\ & \Rightarrow \quad(x+1)^{2}+(y+2)^{2}=\frac{(x-2 y+3)^{2}}{5} \\ & \Rightarrow \quad 5[x^{2}+2 x+1+y^{2}+4 y+4]=x^{2}+4 y^{2}+9-4 x y-12 y+6 x \\ & \Rightarrow \quad 4 x^{2}+y^{2}+4 x+32 y+16=0 \end{aligned} $
46. The equation of the hyperbola with vertices at $(0, \pm 6)$ and eccentricity $\frac{5}{3}$ is …… and its foci are ……
Show Answer
Solution
Let the equation of the hyperbola be $-\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$.
Then vertices $=(0, \pm b)=(0, \pm 6)$
$\therefore b =6 \text { and } e=5 / 3 \\ $
$\because e =\sqrt{1+\frac{a^{2}}{b^{2}}} \Rightarrow \frac{25}{9}=1+\frac{a^{2}}{36} \\ $
$\Rightarrow \frac{25-9}{9} =\frac{a^{2}}{36} \Rightarrow 16=\frac{a^{2}}{4} \Rightarrow a^{2}=48 $
So, the equation of hyperbola is,
$ \begin{aligned} \frac{-x^{2}}{48}+\frac{y^{2}}{36} & =1 \Rightarrow \frac{y^{2}}{36}-\frac{x^{2}}{48}=1 \\ \because \quad \text { Foci } & =(0, \pm b e)=0, \pm \frac{5}{3} \times 6=(0, \pm 10) \end{aligned} $
Objective Type Questions
47. The area of the circle centred at $(1,2)$ and passing through the point $(4,6)$ is
(a) $5 \pi$
(b) $10 \pi$
(c) $25 \pi$
(d) None of these
Show Answer
Solution
(c) Given that, centre of the circle is $(1,2)$.
$\because \quad C P=\sqrt{9+16}=5=$ Radius of the circle
$\therefore \quad$ Required area $=\pi r^{2}=25 \pi$
-
Option (a) $5 \pi$: This option is incorrect because it assumes a radius of $\sqrt{5}$, which is not the correct distance between the center $(1,2)$ and the point $(4,6)$. The actual radius is 5, not $\sqrt{5}$.
-
Option (b) $10 \pi$: This option is incorrect because it assumes a radius of $\sqrt{10}$, which is not the correct distance between the center $(1,2)$ and the point $(4,6)$. The actual radius is 5, not $\sqrt{10}$.
-
Option (d) None of these: This option is incorrect because the correct area of the circle is indeed one of the given options, specifically $25 \pi$.
48. Equation of a circle which passes through $(3,6)$ and touches the axes is
(a) $x^{2}+y^{2}+6 x+6 y+3=0$
(b) $x^{2}+y^{2}-6 x-6 y-9=0$
(c) $x^{2}+y^{2}-6 x-6 y+9=0$
(d) None of these
Show Answer
Solution
(c) Let centre of the circle be $(a, a)$, then equation of the circle is $(x-a)^{2}+(y-a)^{2}=a^{2}$.
Since, the point $(3,6)$ lies on this circle, then
$(3-a)^{2}+(6-a)^{2} =a^{2} \\ $
$ \Rightarrow a^{2}+9-6 a+36-12 a+a^{2} =a^{2} \\ $
$ \Rightarrow a^{2}-18 a+45 =0 \\ $
$ \Rightarrow a^{2}-15 a-3 a+45 =0 \\ $
$ \Rightarrow a(a-15)-3(a-15) =0 \\ $
$ \Rightarrow (a-3)(a-15) =0 \\ $
$ \Rightarrow a =3, a=15 $
So, the equation of circle is
$(x-3)^{2}+(y-3)^{2} =9 \\ $
$\Rightarrow x^{2}-6 x+9+y^{2}-6 y+9 =9 \\ $
$\Rightarrow x^{2}+y^{2}-6 x-6 y+9 =0 $
-
Option (a): The equation (x^{2}+y^{2}+6x+6y+3=0) is incorrect because it does not satisfy the condition that the circle passes through the point ((3,6)). When substituting ((3,6)) into the equation, the left-hand side does not equal zero.
-
Option (b): The equation (x^{2}+y^{2}-6x-6y-9=0) is incorrect because it does not represent a circle that touches the axes. The constant term (-9) indicates that the circle does not have the correct radius to touch both axes.
-
Option (d): This option is incorrect because the correct equation of the circle is provided in option (c). Therefore, “None of these” is not a valid choice.
49. Equation of the circle with centre on the $Y$-axis and passing through the origin and the point $(2,3)$ is
(a) $x^{2}+y^{2}+13 y=0$
(b) $3 x^{2}+3 y^{2}+13 x+3=0$
(c) $6 x^{2}+6 y^{2}-13 y=0$
(d) $x^{2}+y^{2}+13 x+3=0$
Show Answer
Solution
(c) Let general equation of the circle is $x^{2}+y^{2}+2 g h+2 f y+c=0$.
Since the point $(0,0)$ and $(2,3)$ lie on it $c=0$.
$ \begin{matrix} \therefore & 4+9+4 g & +6 f=0 \\ \Rightarrow & 2 g & +3 f=-13 / 2 \\ \text { Since the centre lie on } Y \text {-axis, then } g & =0 . \\ \therefore & 3 f & =-13 / 2 \\ \Rightarrow & f & =-13 / 6 \end{matrix} $
So, the equation of circle is
$ \Rightarrow \quad 6 x^{2}+6 y^{2}-13 y=0 $
-
Option (a): The equation ( x^2 + y^2 + 13y = 0 ) does not satisfy the condition that the circle passes through the point ((2, 3)). Substituting ( x = 2 ) and ( y = 3 ) into the equation does not yield a true statement.
-
Option (b): The equation ( 3x^2 + 3y^2 + 13x + 3 = 0 ) does not have its center on the ( Y )-axis. The presence of the ( 13x ) term indicates that the center has an ( x )-coordinate that is not zero.
-
Option (d): The equation ( x^2 + y^2 + 13x + 3 = 0 ) also does not have its center on the ( Y )-axis. The ( 13x ) term indicates that the center has an ( x )-coordinate that is not zero.
50. The equation of a circle with origin as centre and passing through the vertices of an equilateral triangle whose median is of length $3 a$ is
(a) $x^{2}+y^{2}=9 a^{2}$
(b) $x^{2}+y^{2}=16 a^{2}$
(c) $x^{2}+y^{2}=4 a^{2}$
(d) $x^{2}+y^{2}=a^{2}$
Show Answer
Solution
(c) Given that, length of the median $A D=3 a$
$\because \quad$ Radius of the circle $=\frac{3}{2} \times$ Length of median
$ =\frac{2}{3} \times 3 a=2 a $
So, the equation of the circle is $x^{2}+y^{2}=4 a^{2}$.
-
Option (a): The equation (x^2 + y^2 = 9a^2) is incorrect because it implies that the radius of the circle is (3a). However, the radius of the circle is actually (2a), as derived from the given median length of (3a).
-
Option (b): The equation (x^2 + y^2 = 16a^2) is incorrect because it implies that the radius of the circle is (4a). This is incorrect since the radius of the circle, based on the given median length of (3a), is (2a).
-
Option (d): The equation (x^2 + y^2 = a^2) is incorrect because it implies that the radius of the circle is (a). This is incorrect since the radius of the circle, based on the given median length of (3a), is (2a).
51. If the focus of a parabola is $(0,-3)$ and its directrix is $y=3$, then its equation is
(a) $x^{2}=-12 y$
(b) $x^{2}=12 y$
(c) $y^{2}=-12 x$
(d) $y^{2}=12 x$
Show Answer
Solution
(a) Given that, focus of parabola at $F(0,-3)$ and equation of directrix is $y=3$.
Let any point on the parabola is $P(x, y)$.
Then,
$ P F=|y-3| $
$ \begin{matrix} \Rightarrow & & \sqrt{(x-0)^{2}+(y+3)^{2}} & =|y-3| \\ \Rightarrow & x^{2}+y^{2}+6 y+9 & =y^{2}-6 y+9 \\ & \Rightarrow & x^{2}+12 y & =0 \\ \Rightarrow & x^{2} & =-12 y \end{matrix} $
-
Option (b) $x^{2}=12 y$ is incorrect because it represents a parabola that opens upwards, whereas the given parabola opens downwards due to the negative coefficient in the correct equation $x^{2}=-12 y$.
-
Option (c) $y^{2}=-12 x$ is incorrect because it represents a parabola that opens to the left, whereas the given parabola opens downwards.
-
Option (d) $y^{2}=12 x$ is incorrect because it represents a parabola that opens to the right, whereas the given parabola opens downwards.
52. If the parabola $y^{2}=4 a x$ passes through the point $(3,2)$, then the length of its latusrectum is
(a) $\frac{2}{3}$
(b) $\frac{4}{3}$
(c) $\frac{1}{3}$
(d) 4
Show Answer
Solution
(b) Given that, parabola is
$ y^{2}=4 a x $
$\therefore$ Length of latusrectum $=4 a$
Since, the parabola passes through the point $(3,2)$.
Then,
$ \begin{gathered} 4=4 a(3) \\ a=1 / 3 \\ 4 a=4 / 3 \end{gathered} $
$ \begin{aligned} & \Rightarrow \\ & \therefore \end{aligned} $
-
Option (a) $\frac{2}{3}$ is incorrect because the length of the latus rectum is calculated as $4a$, and with $a = \frac{1}{3}$, the length is $\frac{4}{3}$, not $\frac{2}{3}$.
-
Option (c) $\frac{1}{3}$ is incorrect because the length of the latus rectum is $4a$, and with $a = \frac{1}{3}$, the length is $\frac{4}{3}$, not $\frac{1}{3}$.
-
Option (d) 4 is incorrect because the length of the latus rectum is $4a$, and with $a = \frac{1}{3}$, the length is $\frac{4}{3}$, not 4.
53. If the vertex of the parabola is the point $(-3,0)$ and the directrix is the line $x+5=0$, then its equation is
(a) $y^{2}=8(x+3)$
(b) $x^{2}=8(y+3)$
(c) $y^{2}=-8(x+3)$
(d) $y^{2}=8(x+5)$
Show Answer
Solution
(a) Here, vertex $=(-3,0)$
$\therefore a=-3$ and directrix, $x+5=0$
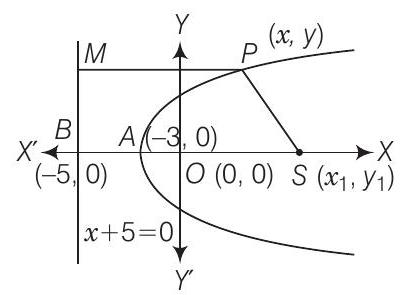
Since, axis of the parabola is a line perpendicular to directrix and $A$ is the mid-point of AS.
$ \begin{matrix} \text { Then, } & -3 & =\frac{x_1-5}{2} \\ \Rightarrow & -6 & =x_1-5 \Rightarrow x_1=-1, \\ & \therefore & 0 & =\frac{0+y_1}{2} \Rightarrow y_1=0 \\ & \therefore & S & =(-1,0) \\ \Rightarrow & P M & =P S \\ \Rightarrow & & x+5 & =\sqrt{(x+1)^{2}+y^{2}} \\ \Rightarrow & x^{2}+2 x+1+y^{2} & =x^{2}+10 x+25 \\ \Rightarrow & y^{2} & =+8 x+24 \\ & & y^{2} & =+8(x+3) \end{matrix} $
-
Option (b) $x^{2}=8(y+3)$: This equation represents a parabola that opens upwards or downwards, with its vertex at $(0, -3)$. However, the given vertex is $(-3, 0)$, so this option is incorrect.
-
Option (c) $y^{2}=-8(x+3)$: This equation represents a parabola that opens to the left, with its vertex at $(-3, 0)$. While the vertex is correct, the directrix for this parabola would be a vertical line to the right of the vertex, not $x+5=0$. Therefore, this option is incorrect.
-
Option (d) $y^{2}=8(x+5)$: This equation represents a parabola that opens to the right, with its vertex at $(-5, 0)$. However, the given vertex is $(-3, 0)$, so this option is incorrect.
54. If equation of the ellipse whose focus is $(1,-1)$, then directrix the line $x-y-3=0$ and eccentricity $\frac{1}{2}$ is
(a) $7 x^{2}+2 x y+7 y^{2}-10 x+10 y+7=0$
(b) $7 x^{2}+2 x y+7 y^{2}+7=0$
(c) $7 x^{2}+2 x y+7 y^{2}+10 x-10 y-7=0$
(d) None of the above
Show Answer
Solution
(a) Given that, focus of the ellipse is $(1,-1)$ and the equation of directrix is $x-y-3=0$ and $e=\frac{1}{2}$
Let $P(x, y)$ and $F(1,-1)$.
$\therefore \quad \frac{P F}{\text { Distance of } P \text { from }(x-y-3=0)}=\frac{1}{2}$
$ \begin{matrix} \Rightarrow & \frac{\sqrt{(x-1)^{2}+(y+1)^{2}}}{\frac{|x-y-3|}{\sqrt{2}}}=\frac{1}{2} \\ \Rightarrow & \frac{2[x^{2}-2 x+1+y^{2}+2 y+1]}{(x-y-3)^{2}}=\frac{1}{4} \\ \Rightarrow & 8 x^{2}-16 x+16+8 y^{2}+16 y=x^{2}+y^{2}+9-2 x y+6 y-6 x \\ \Rightarrow & 7 x^{2}+7 y^{2}+2 x y-10 x+10 y+7=0 \end{matrix} $
- Option (b) is incorrect because it lacks the linear terms (10x) and (-10y) that are necessary to balance the equation derived from the given conditions.
- Option (c) is incorrect because the constant term is (-7) instead of (7), which does not satisfy the derived equation.
- Option (d) is incorrect because option (a) is the correct answer, so “None of the above” cannot be correct.
55. The length of the latusrectum of the ellipse $3 x^{2}+y^{2}=12$ is
(a) 4
(b) 3
(c) 8
(d) $\frac{4}{\sqrt{3}}$
Show Answer
Thinking Process
First of all find the value of $a$ and $b$ from the given equation, after that get length of latusrectum by using formula $\frac{2 a^{2}}{b}$.
Solution
(d) Given equation of ellipse is
$ 3 x^{2}+y^{2}=12 $
$ \begin{aligned} & \Rightarrow \quad \frac{x^{2}}{4}+\frac{y^{2}}{12}=1 \\ & \therefore \quad a^{2}=4 \Rightarrow a=2 \\ & \text { and } \quad b^{2}=12 \Rightarrow b=2 \sqrt{3} \\ & \because \quad b>a \\ & \therefore \quad \text { Length of latusrectum }=\frac{2 \times 4}{2 \sqrt{3}}=\frac{4}{\sqrt{3}}=\frac{2 a^{2}}{b} \end{aligned} $
-
Option (a) 4: This option is incorrect because the length of the latus rectum for an ellipse is given by the formula (\frac{2a^2}{b}). For the given ellipse, (a = 2) and (b = 2\sqrt{3}), which results in (\frac{2 \times 4}{2\sqrt{3}} = \frac{4}{\sqrt{3}}), not 4.
-
Option (b) 3: This option is incorrect because the length of the latus rectum for the given ellipse does not simplify to 3. Using the correct formula (\frac{2a^2}{b}), the result is (\frac{4}{\sqrt{3}}), not 3.
-
Option (c) 8: This option is incorrect because the length of the latus rectum for the given ellipse is calculated using the formula (\frac{2a^2}{b}). For the given values of (a) and (b), the result is (\frac{4}{\sqrt{3}}), not 8.
56. If $e$ is eccentricity of the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ (where, $a<b$ ), then
(a) $b^{2}=a^{2}(1-e^{2})$
(b) $a^{2}=b^{2}(1-e^{2})$
(c) $a^{2}=b^{2}(e^{2}-1)$
(d) $b^{2}=a^{2}(e^{2}-1)$
Show Answer
Solution
(b) Given that,
$ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1, a<b $
We know that,
$ e=\sqrt{1-\frac{a^{2}}{b^{2}}} \Rightarrow e^{2}=\frac{(b^{2}-a^{2})}{b^{2}} $
$ \begin{matrix} \Rightarrow & b^{2} e^{2}=b^{2}-a^{2} \\ \Rightarrow & a^{2}=b^{2}(1-e^{2}) \end{matrix} $
-
Option (a) $b^{2}=a^{2}(1-e^{2})$: This option is incorrect because it suggests that the semi-major axis squared ($b^2$) is equal to the semi-minor axis squared ($a^2$) multiplied by $(1-e^2)$. However, the correct relationship is that the semi-minor axis squared ($a^2$) is equal to the semi-major axis squared ($b^2$) multiplied by $(1-e^2)$, not the other way around.
-
Option (c) $a^{2}=b^{2}(e^{2}-1)$: This option is incorrect because it implies that the semi-minor axis squared ($a^2$) is equal to the semi-major axis squared ($b^2$) multiplied by $(e^2-1)$. This would result in a negative value for $a^2$ since $e^2-1$ is negative for an ellipse (where $e < 1$).
-
Option (d) $b^{2}=a^{2}(e^{2}-1)$: This option is incorrect because it suggests that the semi-major axis squared ($b^2$) is equal to the semi-minor axis squared ($a^2$) multiplied by $(e^2-1)$. This would also result in a negative value for $b^2$ since $e^2-1$ is negative for an ellipse (where $e < 1$).
57. The eccentricity of the hyperbola whose latusrectum is 8 and conjugate axis is equal to half of the distance between the foci is
(a) $\frac{4}{3}$
(b) $\frac{4}{\sqrt{3}}$
(c) $\frac{2}{\sqrt{3}}$
(d) None of these
Show Answer
Solution
(c) Length of latusrectum of the hyperbola i.e.,
$ 8=\frac{2 b^{2}}{a} \Rightarrow b^{2}=4 a $
$\therefore$ Distance between the foci $=2 a e$
Since, transverse axis be $a$ and conjugate axis be $b$.
$ \begin{matrix} \therefore & \frac{1}{2}(2 a e)=2 b \\ \Rightarrow & a e=2 b \\ \Rightarrow & b^{2}=a^{2}(e^{2}-1) \end{matrix} $
From Eqs. (i) and (ii),
$4 a =\frac{a^{2} e^{2}}{4} \\ $
$ \Rightarrow 16 a =a^{2} e^{2} \\ $
$\because 16 =a e^{2} \Rightarrow a=\frac{16}{e^{2}} \\ $
$\Rightarrow 4 a =a^{2}(e^{2}-1) \\ $
$\Rightarrow \frac{4}{a} =e^{2}-1 \\ $
$\Rightarrow \frac{4 e^{2}}{16} =e^{2}-1 $
$ \begin{aligned} \Rightarrow & e^{2} 1-\frac{4}{16} & =1 \\ \Rightarrow & e^{2} \frac{12}{16} & =1 \Rightarrow e^{2}=\frac{16}{12} \\ \Rightarrow & e^{2} & =\frac{4}{3} \Rightarrow e=\frac{2}{\sqrt{3}} \end{aligned} $
-
Option (a) $\frac{4}{3}$ is incorrect because the eccentricity $e$ of a hyperbola must satisfy the equation derived from the given conditions. The correct value of $e^2$ is $\frac{4}{3}$, so $e$ must be $\frac{2}{\sqrt{3}}$, not $\frac{4}{3}$.
-
Option (b) $\frac{4}{\sqrt{3}}$ is incorrect because it does not satisfy the derived equation for $e$. The correct value of $e$ is $\frac{2}{\sqrt{3}}$, and $\frac{4}{\sqrt{3}}$ is not equivalent to this value.
-
Option (d) None of these is incorrect because the correct answer is indeed one of the provided options, specifically option (c) $\frac{2}{\sqrt{3}}$.
58. The distance between the foci of a hyperbola is 16 and its eccentricity is $\sqrt{2}$. Its equation is
(a) $x^{2}-y^{2}=32$
(b) $\frac{x^{2}}{4}-\frac{y^{2}}{9}=1$
(c) $2 x-3 y^{2}=7$
(d) None of these
Show Answer
Thinking Process
The distance between the foci of hyperbola is $2 a$ e and $b^{2}=a^{2}(e^{2}-1)$. Use this relation to set the value of $a$ and $b$.
Solution
(a) Given that, distance between the foci of hyperbola
$ \begin{matrix} \text { i.e., } & 2 a e & =16 \Rightarrow a e=8 \\ \text { and } & e & =\sqrt{2} \\ \text { Now, } & \sqrt{2} a & =8 \\ \Rightarrow & a & =4 \sqrt{2} \\ \because & b^{2} & =a^{2}(e^{2}-1) \\ \Rightarrow & b^{2} & =32(2-1) \\ \Rightarrow & b^{2} & =32 \\ & \therefore & \frac{x^{2}}{32}-\frac{y^{2}}{32} & =1 \\ \Rightarrow & & x^{2}-y^{2} & =32 \end{matrix} $
-
Option (b): The equation (\frac{x^{2}}{4}-\frac{y^{2}}{9}=1) represents a hyperbola, but the given parameters (distance between foci and eccentricity) do not match this equation. Specifically, the values of (a) and (b) derived from this equation do not satisfy the conditions (ae = 8) and (e = \sqrt{2}).
-
Option (c): The equation (2x - 3y^{2} = 7) is not the standard form of a hyperbola. It does not represent a hyperbola at all, as it is a linear equation in (x) and a quadratic equation in (y), which does not fit the general form of a hyperbola (\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1) or (\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1).
59. Equation of the hyperbola with eccentricity $\frac{3}{2}$ and foci at $( \pm 2,0)$ is
(a) $\frac{x^{2}}{4}-\frac{y^{2}}{5}=\frac{4}{9}$
(b) $\frac{x^{2}}{9}-\frac{y^{2}}{9}=\frac{4}{9}$
(c) $\frac{x^{2}}{4}-\frac{y^{2}}{9}=1$
(d) None of these
Show Answer
Solution
(a) Given that, eccentricity of the hyperbola, $e=3 / 2$
and
$\because$
$\Rightarrow$
$\because$
$\Rightarrow$
$\Rightarrow \quad b^{2}=\frac{20}{9}$
So, the equation of the hyperbola is
$ \frac{x^{2}}{\frac{16}{9}}-\frac{y^{2}}{20 / 9}=1 \Rightarrow \frac{x^{2}}{4}-\frac{y^{2}}{5}=\frac{4}{9} $
$ \begin{aligned} \text { foci } & =( \pm 2,0),( \pm a e, 0) \\ a e & =2 \\ a \times 3 / 2 & =2 \Rightarrow a=4 / 3 \\ b^{2} & =a^{2}(e^{2}-1) \\ b^{2} & =\frac{16}{9} \frac{9}{4}-1 \Rightarrow b^{2}=\frac{16}{9} \frac{5}{4} \\ b^{2} & =\frac{20}{9} \end{aligned} $
-
Option (b): The equation $\frac{x^{2}}{9}-\frac{y^{2}}{9}=\frac{4}{9}$ is incorrect because it does not match the standard form of a hyperbola with the given eccentricity and foci. The denominators for $x^2$ and $y^2$ should be different, reflecting the relationship between $a^2$ and $b^2$ derived from the given eccentricity and foci.
-
Option (c): The equation $\frac{x^{2}}{4}-\frac{y^{2}}{9}=1$ is incorrect because it does not satisfy the condition for the given eccentricity and foci. Specifically, the value of $a^2$ should be $\left(\frac{4}{3}\right)^2 = \frac{16}{9}$, not 4, and the value of $b^2$ should be $\frac{20}{9}$, not 9.






