Motion
Multiple Choice Questions
1. A particle is moving in a circular path of radius
(a) Zero
(b)
(c)
(d)
Show Answer
Answer
Answer is (c)
Explanation:
After half revolution
Path length
Displacement
It comes out to be the diameter of the circle
(a)
(b)
(c)
(d)
Show Answer
Answer
Answer is (b)
Explanation:
here
(a) always less than 1
(b) always equal to 1
(c) always more than 1
(d) equal or less than 1
Show Answer
Answer
Answer is (d) equal or less than 1
Explanation:
Shortest distance between initial and end point is called displacement. Distance is the total path length.
Displacement is vector and it may be positive or negative whereas Distance is scalar and it can never be negative.
Distance can be equal or greater than displacement which means ratio of displacement to distance is always equal to or less than 1 .
(a) uniform velocity
(b) uniform acceleration
(c) increasing acceleration
(d) decreasing acceleration
Show Answer
Answer
Answer is (b) uniform acceleration
Explanation:
Velocity is measured in distance /second and acceleration is measured in Distance/ second
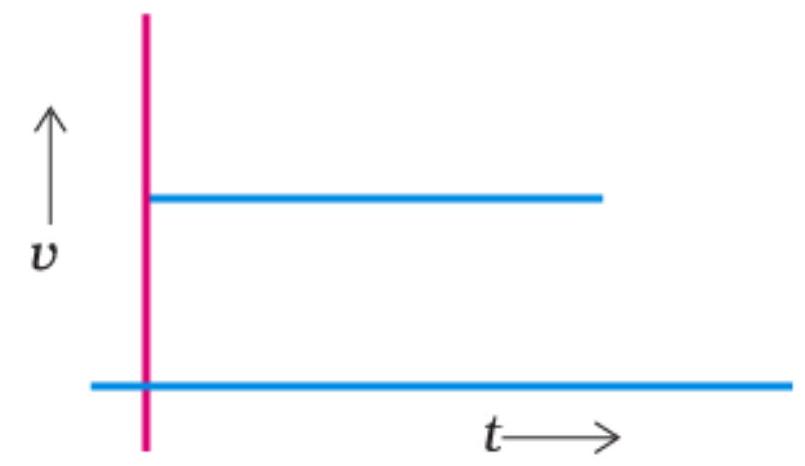
(a) in uniform motion
(b) at rest
(c) in non-uniform motion
(d) moving with uniform acceleration
Show Answer
Answer
Answer is (a) in uniform motion
Explanation:
From the above given graph it is clear that velocity of the object remain constant throughout hence the object is in uniform motion.
(a) at rest
(b) moving with no acceleration
(c) in accelerated motion
(d) moving with uniform velocity
Show Answer
Answer
Answer is (c) in accelerated motion
Explanation:
Boy is moving in a circular motion and circular motion is an accelerated motion hence C) is right answer.
(a)
(b)
(c)
(d)
Show Answer
Answer
Answer is (b)
Explanation:
Area given in the graph represents Displacement and its unit is meter. Hence the answer is (b)
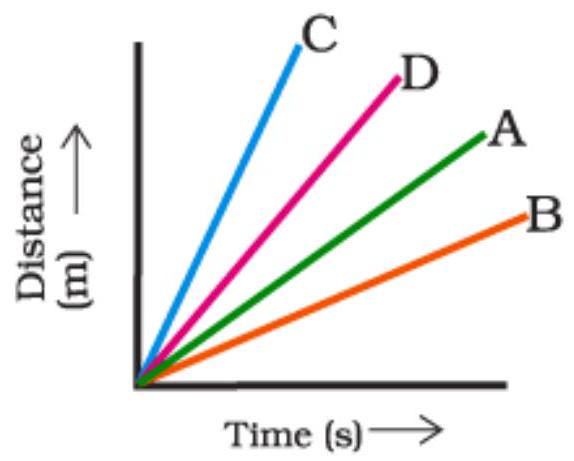
(a) Car
(b) Car
(c) Car D is faster than car C.
(d) Car
Show Answer
Answer
Answer is (b) Car B is the slowest.
Explanation:
Graph shows that Car B covers less distance in a given time than A, C and D cars hence it is the the slowest.
 a
a
 b
b
 c
c
 d
d
Show Answer
Answer
Answer is (a)
Explanation:
Distance in graph (a) is uniformly increasing with time hence it represents uniform motion.
(a) the distance
(b) the displacement
(c) the acceleration
(d) the speed
Show Answer
Answer
Answer is (c) the acceleration
(a) If the car is moving on straight road
(b) If the car is moving in circular path
(c) The pendulum is moving to and fro
(d) The earth is revolving around the Sun
Show Answer
Answer
Answer is (a) If the car is moving on straight road
Explanation:
In other cases given here displace can be less than distance hence option (a) If the car is moving on straight road is the right answer.
Short Answer Questions
12. The displacement of a moving object in a given interval of time is zero. Would the distance travelled by the object also be zero? Justify you answer.
Show Answer
Answer
Displace zero does not mean zero distance. Distance can be zero when moving object back to the place it started. Displacement is either equal or less than distance but distance is always greater than one and it cannot be a negative value.
Show Answer
Answer
If object moving in a uniform velocity then
Show Answer
Answer
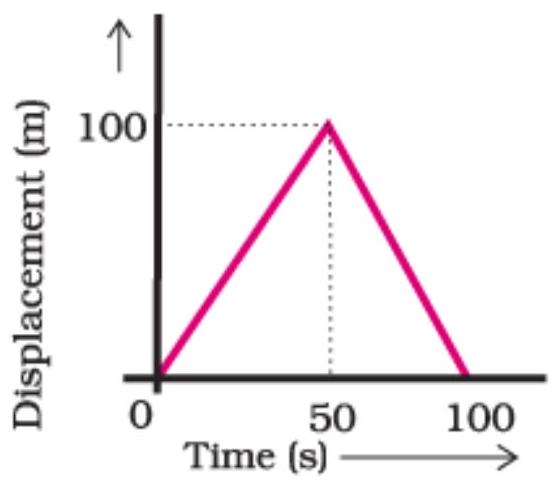
Show Answer
Answer
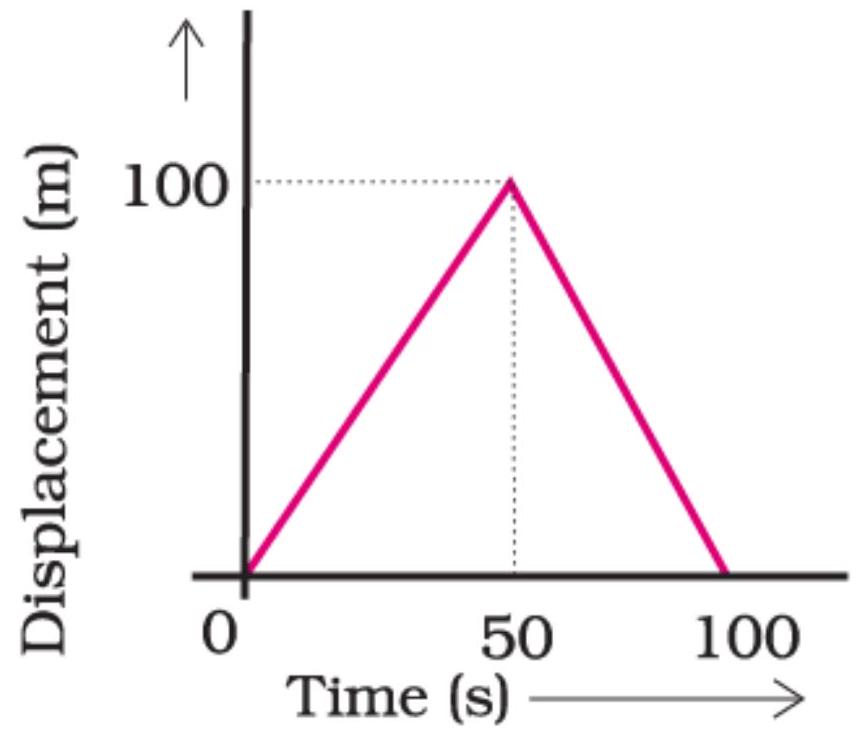
Car Starts from rest hence Initial velocity
From second equation
Show Answer
Answer
Let the distance from
Distance for the entire journey is
Time taken to go from A to B is D/30 hr and that of B to A is D/20 hr. So, total time taken T
Average speed
Av.speed
Hence Average speed of the motocycle is
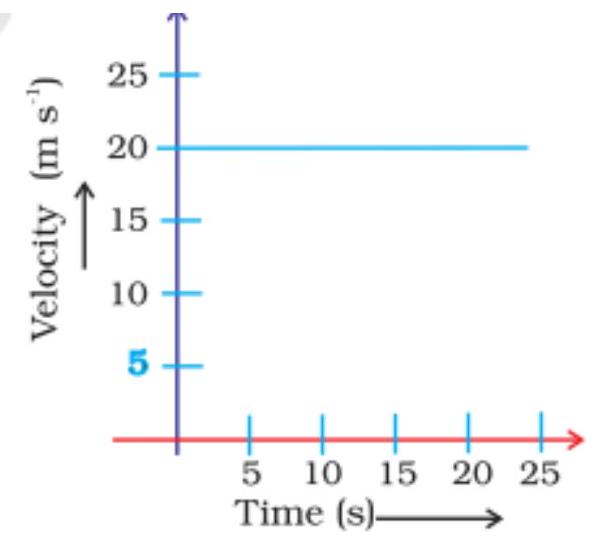
Fig. 8.5
Show Answer
Answer
Here Velocity is constant hence
(iii)
Show Answer
Answer
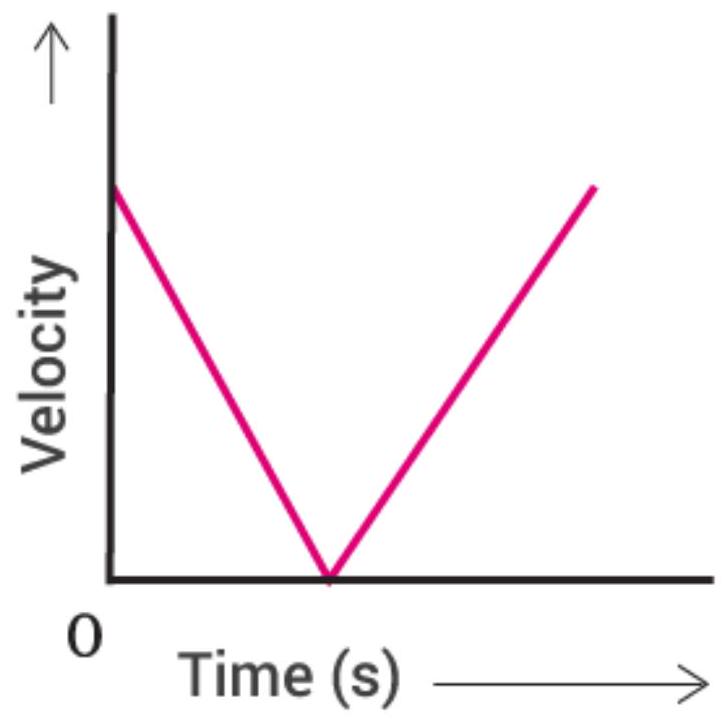
Show Answer
Answer
When two objects fall with same acceleration simultaneously. after 2 seconds the difference in their heights will not change and it remain
Therefore the height of first object after 2 seconds is
In the same way the height of second object is
Therefore, the height of second object after 2 seconds is
So, the difference is same, i.e.
This concludes that the difference in height of the two objects does not depend on time and will always be same.
Show Answer
Answer
Here Object starts from rest hence initial velocity
According to Second equation of motion
According to first equation of motion velocity after
| Time(s) | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
|---|---|---|---|---|---|---|---|---|---|
| Displacement(m) | 0 | 2 | 4 | 4 | 4 | 6 | 4 | 2 | 0 |
Use this graph to find average velocity for first
Show Answer
Answer
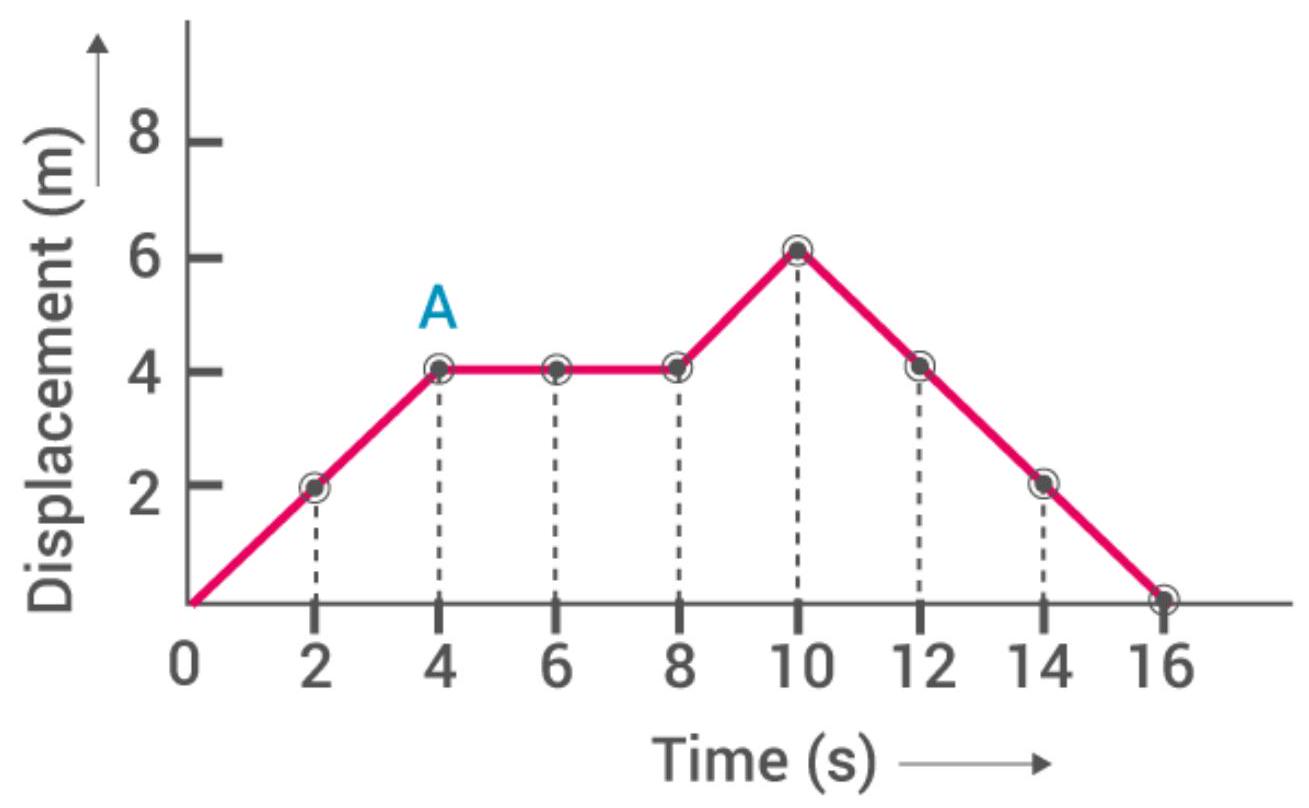
Average velocity for the first
Average velocity of next
Average velocity for last
(i) Calculate the time in which the electron would acquire a velocity double of its initial velocity.
(ii) How much distance the electron would cover in this time?
Show Answer
Answer
Given initial velocity,
(i) final velocity
To find
(ii)
Using
Show Answer
Answer
Assume that air resistanceis nil.
We can directly contain it by using Newton’s equations of motion or from the below mentioned method:
Thus area under the v-t curve and the x-axis where the slope of the curve is the instantaneous acceleration.
In this case acceleration
On dividing the total area under the curve into interval of unit seconds, then we initially obtain a triangle followed by trapeziums of increasing height.
The ratio of area of first triangle to second triangle to third triangle is equal to the ratio of displacement in first, second and third second. We get ratio equal to 1:3:5:7:9… and so on.
For 4 th & 5th second it is 7:9.
Show Answer
Answer
We know for upward motion,
But at highest point
Therefore,
For first ball,
and for second ball,
Thus










